基于模糊层次分析法的干式变压器运行状态综合评估

2013-07-06赵艳龙徐敏捷席朝辉王海英

重庆理工大学学报(自然科学) 2013年4期

赵艳龙，熊兰，徐敏捷，席朝辉，王海英

(1.重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆 400030;2.重庆市电力公司检修分公司，重庆 400014;3.鹤壁市机电信息工程学校，河南鹤壁 458030)

近年来，随着电网负荷的不断增加，干式变压器由于其突出的优点而被广泛使用［1］。但是，干式变压器在运行中由于绝缘击穿而造成爆炸起火的事故时有发生［2］，不仅对现场运行人员的人身安全造成威胁，同时也影响电网的安全、平稳运行。

目前，对干式变压器运行状况的判断主要是通过监测其温度、湿度、电压、电流和功率等参数来实现的［3-4］。其中，绕组温度可以在一定程度上反映干式变压器的内部绝缘情况，当温度值或温升值超过阈值时，就要进行停电检修等作业。但是这些方法都只是基于某一参量的状态分析方法，并不能科学地评估出干式变压器的运行状况及状态发展趋势。

变压器运行状态受多种因素的影响，其运行状态也处在动态的发展变化中［5-8］，这就需要建立变压器运行状态综合评估模型。通过对数据的实时分析，综合评估变压器的运行状况及可能的缺陷发展趋势，就可以确定变压器进行检修的时间和故障点。

本文基于模糊层次分析法(FAHP)对干式变压器运行状态进行综合评判。首先对影响干式变压器运行状态的各类参量进行分析，确定评判指标体系。然后利用FAHP方法确定各指标因素的权重，依据均衡函数的变权理论，根据评判因素偏离正常值的水平，对各指标的固定常权进行修正。最后根据建立的多层模糊评判方法对干式变压器运行状态进行综合评估。

1 模糊层次分析法

模糊层次分析法(FAHP)是建立在层次分析法(AHP)基础之上的一种更加实用有效的分析方法。层次分析法(AHP)是美国运筹学家 T.H.Sauty于20世纪70年代提出的一种解决目标决策问题的方法［9-12］。该方法将决策问题的有关元素分解成目标、准则、方案等层次，在此基础上进行定性分析和定量分析相结合的多目标决策分析。

层次分析法(AHP)的关键环节是建立判断矩阵，判断矩阵是否科学合理将直接影响到AHP的效果。研究发现，AHP中检验判断矩阵是否一致非常困难。为了解决这个问题，研究人员在层次分析法中引入了模糊一致矩阵的概念，从而得到了模糊层次分析法(FAHP)［13-14］。

模糊层次分析法(FAHP)可以分为5个步骤:

①建立问题的层次结构，确定目标和评价因素集。

② 构造优先关系矩阵F=(fij)n×n，确定各因素间的相互关系。

③利用定理将优先关系矩阵F转换成模糊一致矩阵R。

④进行层次单排序，即根据模糊一致判断矩阵推算本层次各因素对上层因素的重要性次序。

⑤进行层次总排序，即对各层次因素重要性进行总排序。

2 评估指标体系的建立

2.1 评判因素集的确定

为了能更加真实、全面地反映干式变压器的运行状况，依据全面、主导、可操作性、系统与层次相结合的原则，在广泛征求现场运行人员意见的基础上，从固有特性、运行工况、运行环境和运行历史4个方面选择了16种状态参量作为评判因素，建立干式变压器运行状态评判指标体系，如图1所示。

指标体系由目标、项目和指标3个层次组成。其中目标层为干式变压器运行状态UX，分解为项目层中的 4 个评判项目 UX=(UX1，UX2，UX3，UX4)，每个评判项目中又包含4个评判指标，组成指标层。指标层中，运行工况X2和运行环境X3的4个指标及使用年限X41这9个为定量指标，其余7个为定性指标。

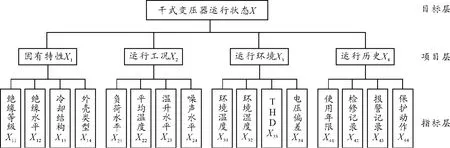
图1 干式变压器运行状态评判指标体系

2.2 评语集的确定

确定评估因素后，需划分干式变压器运行状态的等级。等级划分不宜太多或太少。分级太少，拉不开档次;分级太多，评估结构过于分散，而且计算量也会增加，造成评判的延迟时间较长。

根据实际情况，将干式变压器的运行状态划分为良好、一般、注意、严重4个等级，即V={良好、一般、注意、严重}={V1，V2，V3，V4}。良好(V1)表示干式变压器整体性能良好，运行状态稳定。一般(V2)表示干式变压器整体性能有所下降，运行状况基本能满足需求，发生故障的可能性比较小，运行时需要多跟踪观察。注意(V3)表示干式变压器整体性能下降较大，存在可能损坏变压器的风险，运行能进行，但是发生故障的可能性较大，有条件时应进行检修。严重(V4)表示干式变压器整体性能下降严重，某些部位可能已经损坏，运行严重不正常，需立即停电检修或是更换变压器。

3 权重的确定

3.1 常权确定

对于各评判因素常权主要是基于模糊层次分析法(FAHP)进行确定。根据FAHP方法的分析步骤，首先需要对项目层和指标层相关因素之间建立优先关系矩阵F，确定各因素之间的相对重要性，然后通过层次排序计算后确定各评判因素的常权。

矩阵 F 采用0.1 ～0.9 标度法构造［14］，如表 1所示。构造的优先关系矩阵F是模糊互补矩阵。

根据所建立的评判指标体系可知，共需要在项目层建立1个优先关系矩阵，在指标层建立4个优先关系矩阵。

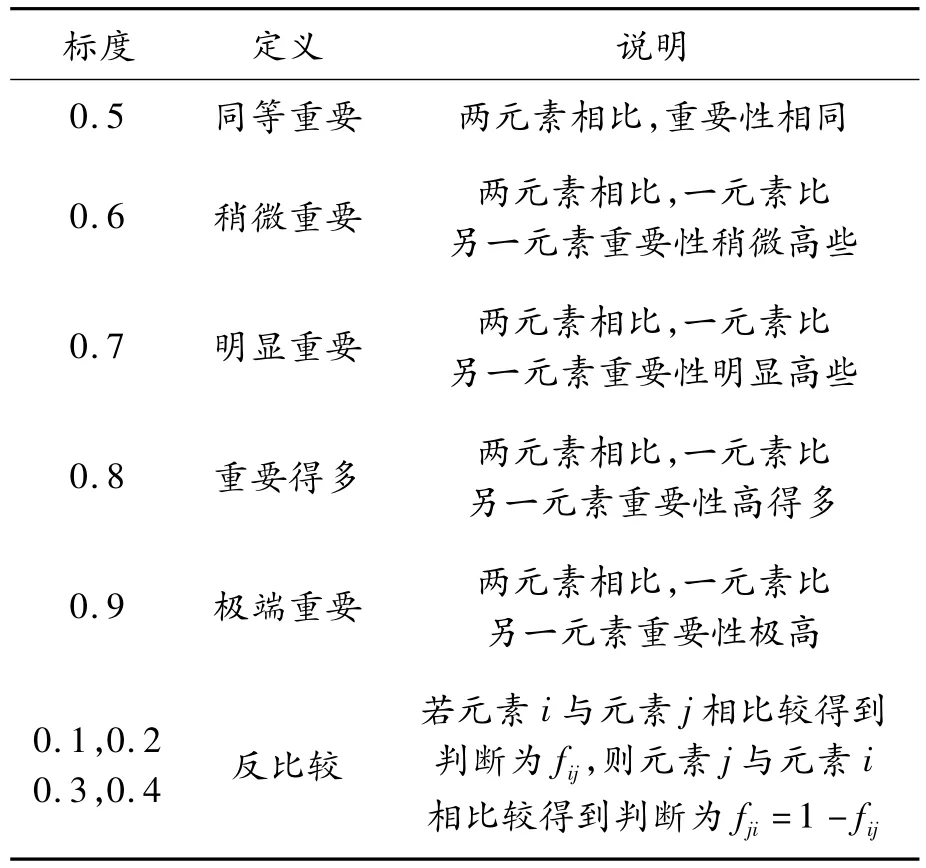
表1 0.1 ～0.9 标度的定义

在参照国家相关技术标准［15］，同时广泛征求专家和现场运行人员意见的基础上，确定项目层4个因素中运行工况是直接反映变压器运行状态的参量，重要性最为突出。运行历史对于干式变压器运行影响重要性小于运行工况，但是比运行环境要稍微强些。与其他3个因素相比固有特性对于干式变压器运行状况影响相对最弱。因此，项目层的优先关系矩阵F1表示为:

根据定理1将优先关系矩阵F1转换为模糊一致矩阵R1:

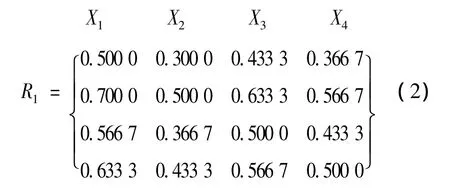
根据求得的模糊一致矩阵，通过层次排序计算来推出各因素的常权值。常用的层次排序计算方法有方根法、行和归一法、因素关系法［9］。其中因素关系法所求得的最大权重和最小权重之间的差距最大，分辨率最高，各因素之间权重区别比较明显，因而本系统采用因素关系法所求得的权重作为各因素的常权值。

因素关系法的计算表达式为:

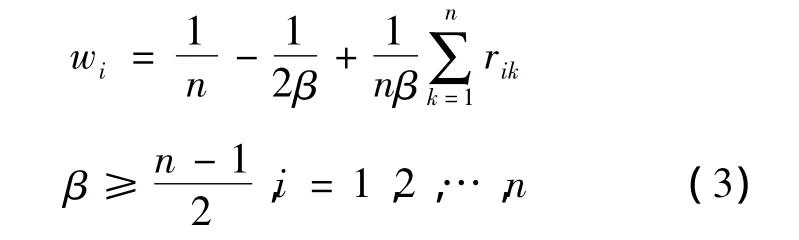
其中β越小，权重之差越大。当β=(n-1)/2时，权重之差达到最大值。因此，为了重视元素间重要程度差异，实际应用中常取β=(n-1)/2。

依据因素关系法所计算的项目层各因素的常权值，如表2所示。

表2 项目层各因素常权值

根据以上求解方法，可以求出指标层各因素的常权值，如表3所示。

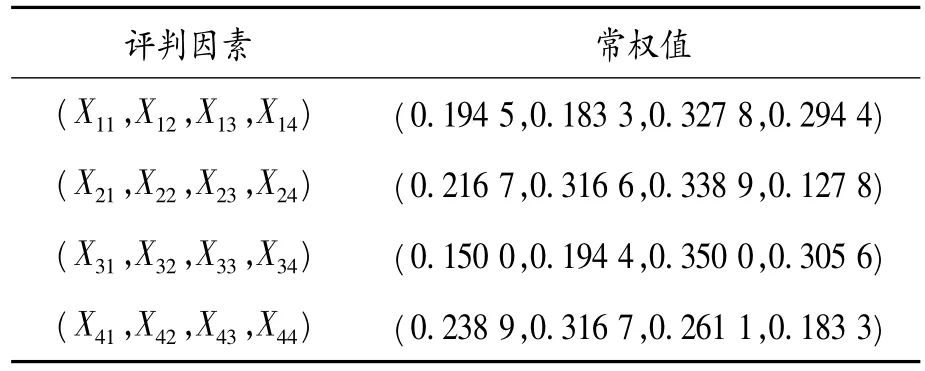
表3 指标层各因素常权值

3.2 变权理论

用模糊层次分析法(FAHP)确定的各因素权重是固定的，不会因为状态或评判因素的不同而发生改变。而在干式变压器运行状态评判指标体系中，当某些参数严重偏离正常值时，往往代表干式变压器的某部分性能急剧下降，这时需要立即停电检修，否则可能引发一系列连锁反应，严重时将导致爆炸、起火等事故发生。但是在常权评判模型中可能会因为其权重相对较小，给出的综合评判结果还是能维持运行的状态，这将不能真实地反映干式变压器的运行状态。因此，本系统引入变权理论。

汪培庄等［14］于20世纪80年代提出了变权思想，并给出了变权经验公式，由经验公式出发对变权综合进行了深入的分析，给出了变权、状态变权向量和均衡函数的公理化定义，使变权理论有了完整的体系，其提出的变权公式为

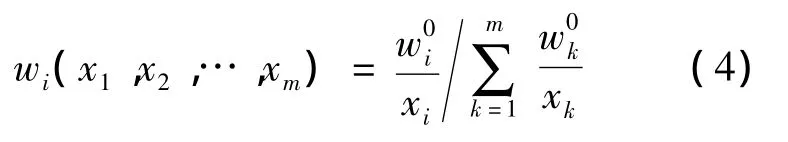
其中:xi为第i个评判因素的值;m为评判因素个数;wi为第i种因素的变权重;为第i种因素的常权重。

也有学者在变权理论体系的基础上，将均衡函数引入了变权综合。当采用变权综合模式Ⅰ时，均衡函数为

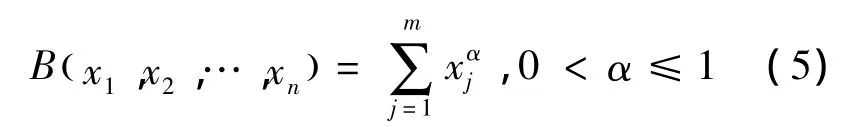
其改进的变权公式为

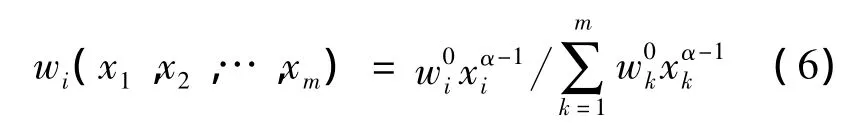
一般来讲，在评判者较保守的情况下，α＜0.5，此时对各因素的平衡问题考虑得较多;在评判者较开明的情况下，α＞0.5，此时比较能容忍某方面的缺陷;α=1时，等同于常权综合模式。在多数情况下，α取0.5为宜。对于干式变压器运行状态评判而言，考虑到关键参数严重偏离正常值时将影响整个变压器的安全稳定，因此，本系统中对于运行工况的指标层取α=0.2，其他的指标取α =0.5。

4 评判因素隶属函数的确定

隶属度函数是模糊集合应用于实际问题的基础，其确定方法不是唯一的，关键在于能否正确反映元素隶属集合到不属于集合这一变化过程的整体集合。本文根据定量指标和定性指标，应用2种不同的隶属度函数。

4.1 定量指标隶属函数

对于不同的定量指标，由于各指标的量纲和数量级不同，无法直接进行综合评判。因而在确定隶属函数之前，需对其进行归一化处理［16-17］。归一化处理采用如下方法:

对于越小越优型指标，计算公式为

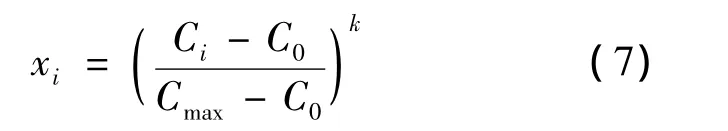
对于越大越优型指标，计算公式为

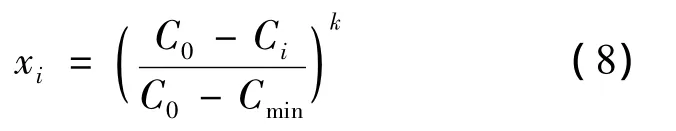
其中:xi为第i个指标的归一化值;C0为该指标的允许值(良好值);Cmax或Cmin为该指标的极限值，主要参考国家对于干式电力变压器及电能质量的相关标准［11］;Ci为该指标的实测值;k为参数变化对设备状态的影响程度，在本系统中取为1。

归一化处理后的定量指标，对其采用模糊分布法。岭形分布具有主值区间宽、过度地带平缓等特点，能很好地反映指标与状态之间的模糊关系，因此，采用半梯形和半岭形相组合的分布函数来确定各定量指标的隶属度。其隶属函数分布如图2所示。

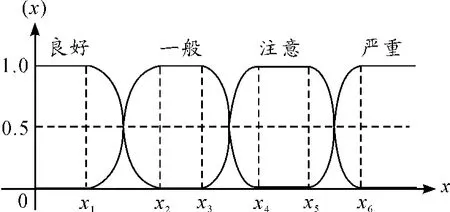
图2 半梯形和半岭形结合的隶属度函数分布

对于模糊分界区间的选定，不同的指标选取不同的值。主要参考的是国家标准，同时结合现场运行的统计数据，例如，认定温升水平指标属于越小越优型指标。F级绝缘等级的干式变压器最高温升限值为100℃［15］，其归一化处理函数为x=Ci/100，当 Ci＞100 时，x取值为1，Ci为实测的温升值。其对应的V1～V4四种状态的隶属度函数表达如下:

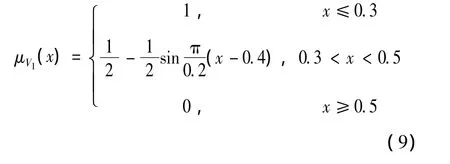
同理，可以得到指标层中其他定量指标的隶属函数，在此不一一叙述。

4.2 定性指标的隶属函数

对于检修记录、报警记录、保护动作等定性指标采用专家评分方式，评分区间为［0～1］，分值越大，指标越优。通过对现场数据进行统计，制作调查表分发给各位专家，专家依据现场数据情况对该指标的状态进行评分。然后，对各专家评分进行综合，得出评判因素的隶属度，其表达式为

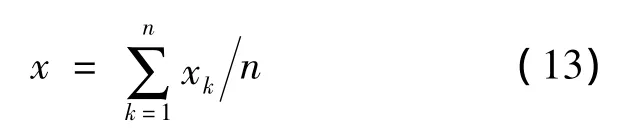
其中:x为定性指标的隶属度;xk为各位专家对于该指标的评分值;n为参加评定的专家总人数。

考虑到专家评分情况，主要依靠专家经验和看法，有一定的主观因素，因此，采用半梯形和三角形相结合的隶属函数来进行评判，其隶属函数分布如图3所示。

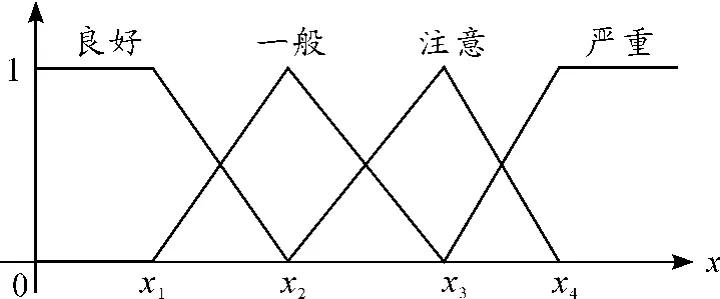
图3 半梯形和三角形结合的隶属函数分布

5 干式变压器的运行状态综合评估

5.1 模糊综合评判

通过建立指标的隶属度函数后，可以得出因素xi的单因素评估集。

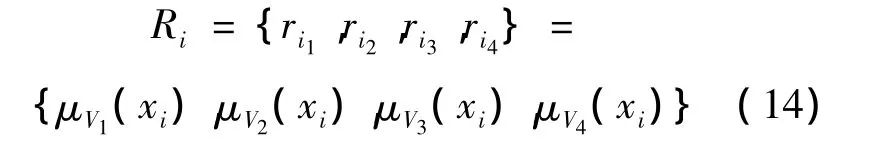
分别以各单因素评估集为行可以建立起单因素评判矩阵R，其中m为指标数。

单因素模糊评判仅反映了一个因素对于评估对象的影响，这显然是不够准确的，为此要综合考虑所有因素的影响，将各因素的权重值引入模糊矩阵，从而得到模糊综合评判集B。

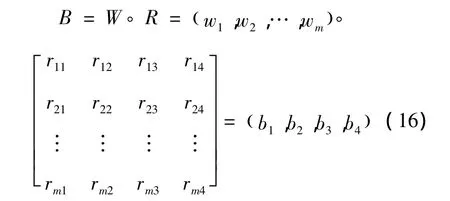
式中:W为指标权重集;wi(i=1，2，…，m)为各评判因素的权重;“◦”为模糊合成算子;bj(j=1，2，3，4)为模糊综合评价指标。

式(16)中对于模糊合成算子“◦”选择比较重要，不同算子含义不同，适用情况也不尽相同［18］。文献［18］综合分析了常见的4种算子各自的特性及优缺点，本文在此基础上选择使用加权平均型算子M(·，⊕)。

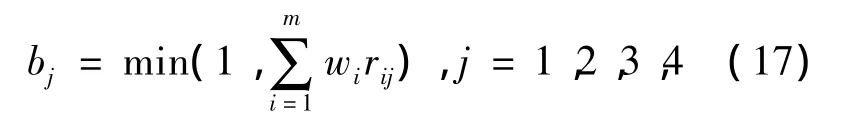
该算子不仅考虑了所有因素的影响，而且保留了单因素评判的全部信息，比较适合于要求整体指标的评估。

5.2 等级确定

经过模糊综合评判得到评估指标bj(j=1，2，3，4)之后，必须对评估指标进行处理，以得到最终的评判结果。目前，对评估指标处理的方法主要包括最大隶属度法、加权平均法、模糊分布法［19］。其中加权平均法由于综合反映了各因素的权重及隶属度对评判结果的影响而得到广泛使用，本研究即采用此方法。

加权平均法的基本思想是利用评价结果中各个评语等级的隶属度形成权重，即以bj为权重数，对各个评语集元素Vi经行加权，求得综合值作为评判的结果，其表达式为

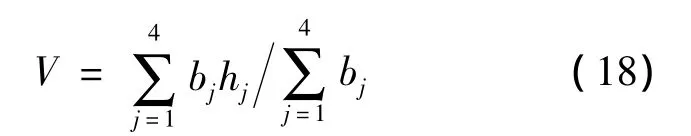
式中:hj为V1～V4四种状态所对应的分值，分别为1～4;bj为经过模糊综合评判得到的评估指标。

6 实例分析

某供电局一台10 kV开闭所站用干式变压器，型号为 SCB10-315/10，10.5 ±2 ×2.5%/0.4 kV，Dyn11联结，绝缘等级为 F级，温升极限为100℃，额定容量为315 kVA，额定电流为17.3/454.7A。干式变压器冷却方式为AN/AF，即设有封闭的保护外壳，内部采用空气强迫循环冷却的方式，外部采用空气自然循环的方式。

通过安装在现场的干式变压器综合监测系统显示，某时段负荷为213 kVA，三相运行平均温度为53.6℃，现场环境温度为30.3℃，相对湿度为64.3%，平均温升为23.3℃。通过多点测量，计算出干式变压器的声功率级为56 dB(A)，母线电压总谐波畸变率 THD为 0.89%，母线相电压为5 990 V，母线电压最大偏差为3.74%。

该变压器使用年限为5年，曾做过2次全面检修，每2年一次，分别对铁心、绕组进行检查，并对绝缘电阻进行测试，其中第2次检修时发现铁心表面有小部分污渍，测试绝缘电阻为4 MΩ，满足大于2 MΩ的要求。报警记录显示有2次高温报警，温升最大值分别达到80℃、85℃;还有3次过流报警，负荷电流最大值分别达到465、502、485 A，曾有一次过流保护开关动作。

通过以上实际数据，对该干式变压器的运行状态进行评判。

1)计算指标层各指标的变权值，如表4所示。

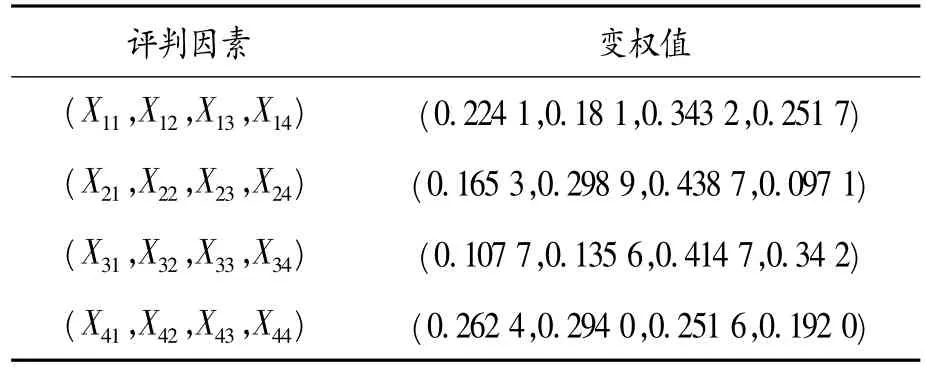
表4 指标层各因素变权值

2)对各项目进行评估。按照各因素的隶属度函数，分别计算固有特性、运行工况、运行环境和运行历史中各因素对应于4种状态的隶属度，得到评判矩阵。例如运行工况的评判矩阵为

结合运行工况的变权值，可得

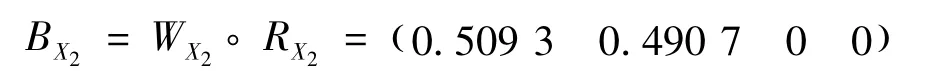
同理，可得到:

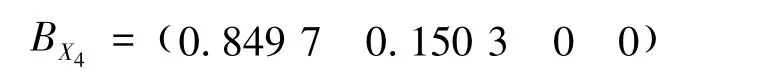
3)干式变压器整体运行状态评估。根据项目层各因素的常权值，求得干式变压器整体运行状态的评估指标。

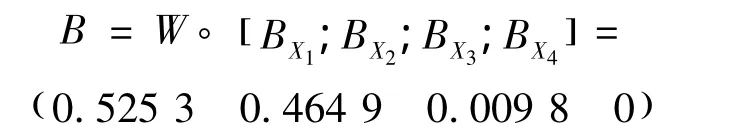
4)评估结果的确定。将良好、一般、注意、严重4种等级分别赋值 1、2、3、4，利用式(18)对 B进行加权平均后求的V=1.485。该结果表明:由评估模型得到的干式变压器运行状态在良好和一般中间。实际情况为干式变压器处于低负荷运行，温升比较低。停电检修后发现干式变压器各部分性能良好，除风道处有少部分污渍外无其他损坏，能维持干式变压器稳定运行。