基于槽口优化的电动汽车用大功率无刷直流电机齿槽转矩削弱方法
2013-07-06王晓远
王晓远 贾 旭
(天津大学电气与自动化工程学院 天津 300072)
1 引言
无刷直流电机结构简单、维护方便、功率密度高、可靠性高,但由于存在转矩脉动使其在电动汽车上的应用受到很大限制,特别是大功率无刷直流电机尤为突出,而齿槽转矩是转矩脉动产生的主要原因[1]。目前,对于中小功率无刷直流电机,可以采用多种有效方法抑制齿槽转矩,如采用分数槽绕组、优化极弧系数、合理设计磁极形状、斜槽、斜极、极槽组合法[2-14]等,但这些方法通过消去特定谐波往往会使无刷直流电机的反电动势偏离梯形波而接近正弦波,由于按方波进行驱动控制的无刷直流电机所产生的方波电流与正弦波反电动势相互作用会产生明显的转矩脉动,因此对于电动汽车用大功率方波无刷直流电机,采用分数槽绕组、斜槽、斜极等方法抑制齿槽转矩是不合理的。为此,本文提出一种优化槽口偏移角度和槽口宽度的方法,通过合理调整槽口部分的磁通分布来减小齿槽转矩,由于只有槽口偏移,定子槽和定子槽内的绕组并没有偏移,所以避免了因绕组滤波效应而引起的反电动势波形变化。
对于多因素试验,传统的试验方法每次只能针对一个因素进行试验,同时必须保证其他因素的值不变,这样不仅增加了试验次数,而且不能反映各因素之间的相互作用。本文所采用的响应面法能够克服传统试验方法的这些缺点,同时针对槽口偏移角度和槽口宽度两个因素进行试验,并计算出齿槽转矩与槽口偏移角度和槽口宽度之间的数学模型,得到最优解组合。
本文以自行设计的一台30kW、4 极12 槽电动汽车用无刷直流电机作为研究对象,采用试验设计方法优化电机定子槽口偏移角度和槽口宽度,得到使齿槽转矩最小的槽口偏移角度和槽口宽度最佳组合,最后用有限元方法验证了所得结果的正确性。
2 齿槽转矩的抑制方法
为深入研究槽口偏移和槽口宽度对大功率无刷直流电机齿槽转矩的影响,初步设计一台功率为30kW的电动汽车用无刷直流电机,其主要参数见表1。
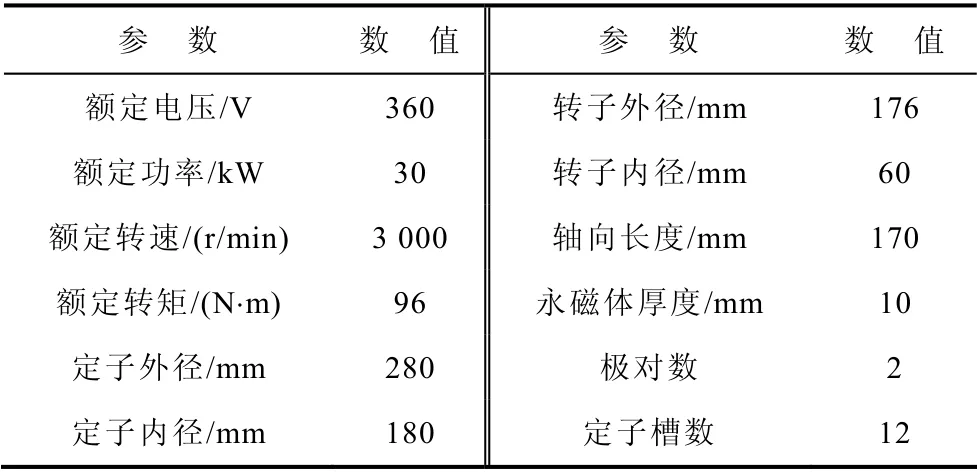
表1 无刷直流电机参数Tab.1 Parameters of BLDC
下面,以该电机作为研究对象,通过合理组合槽口偏移角度和槽口宽度抑制该电机的齿槽转矩。
文献[15]以一台6 极18 槽的无刷直流电机作为研究对象,提出一种槽口偏移模型,如图1 所示。它将每个磁极对应的三个槽分为一组,每组内中间的槽口不偏移,左侧的槽口向右偏移,右侧的槽口向左偏移。图2 所示为本文所提出的槽口偏移无刷直流电机模型,与文献[15]的偏移方式不同,该模型并没有对电机槽口进行分组,而是相邻两个槽口的偏移方向相反,此外,本文所优化的变量不只槽口偏移角度一个,而是同时对槽口偏移角度和槽口宽度进行优化。
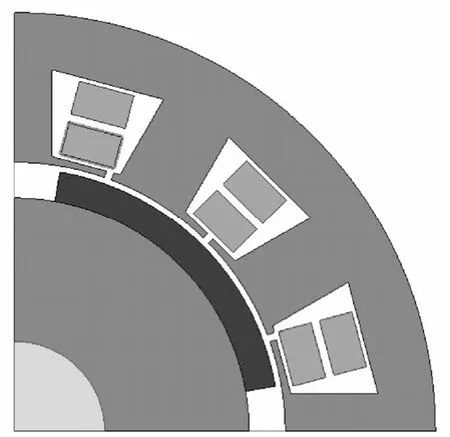
图1 文献[15]所提出的无刷直流电机槽口偏移模型Fig.1 Slot opening shift model of PM BLDC in paper[15]

图2 本文所提出的槽口偏移的无刷直流电机模型Fig.2 Slot opening shift model of PM BLDC in this paper
为了便于定量分析槽口偏移角度和槽口宽度对无刷直流电机齿槽转矩的影响,图3 给出了无刷直流电机的定子简化模型。槽口偏移角度β的起点以定子槽中心线为基准,由于电机定子槽宽度限制,槽口偏移角度β的范围为0°~6°,相邻两槽口的偏移角度相等,偏移方向相反。槽口宽度λ的取值范围为2~3mm。
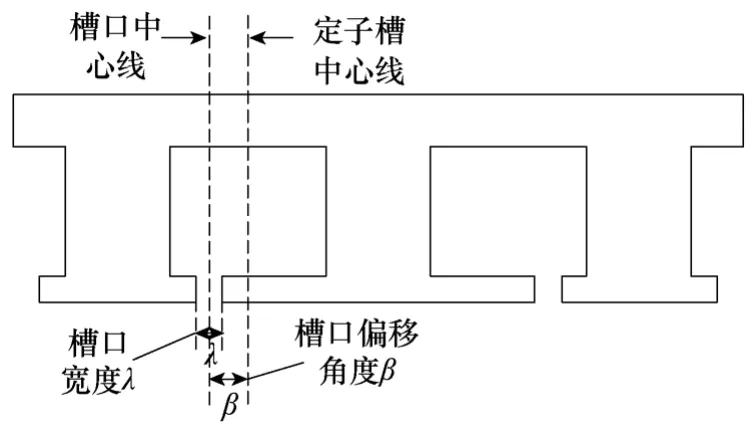
图3 槽口偏移后的定子齿槽简图Fig.3 Simplified diagram of slot opening shift stator slot
如图4 所示当β=2.2、λ=2.5,β=3、λ=2 以及β=0、λ=2.5(初始电机模型)时的无刷直流电机齿槽转矩波形对比,由图可以看出,与初始电机齿槽转矩相比,槽口偏移后的无刷直流电机的齿槽转矩幅值明显减小,而且,不同槽口偏移角度β和槽口宽度λ组合对齿槽转换的削弱效果并不相同。由此可见,在槽口偏移角度与槽口宽度的取值变化范围内,一定存在最佳的槽口偏移角度和槽口宽度组合,使得无刷直流电机齿槽转矩最小。下面就应用响应面法(RSM)寻求最优槽口偏移角度和槽口宽度组合。
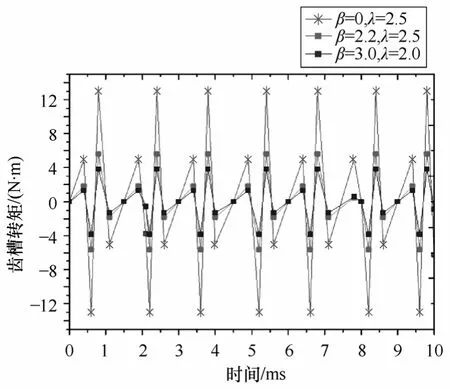
图4 β =2.2、λ=2.5 与电机初始模型齿槽转矩对比Fig.4 The comparison of cogging torque between initial model and optimum model when β=2.2、λ=2.5
3 响应面法寻求最优槽口偏移角度和槽口宽度组合
响应面法(RSM)是一种最优化方法,当某个响应受多个自变量的影响时,利用响应面法能够寻求目标响应的最优解。通常,响应面可表示为[16]
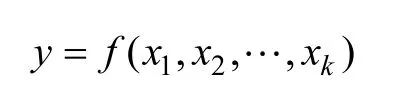
式中,k为变量个数。
一般情况下,响应与自变量之间的关系可用二次多项式表示,二次多项式的一般形式为[16]
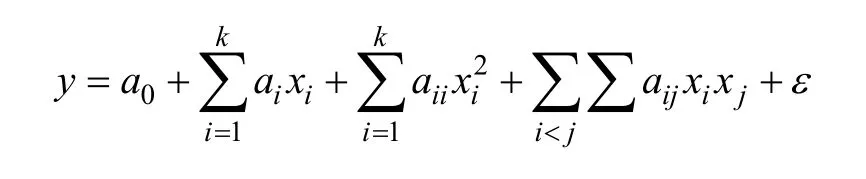
本文选取无刷直流电机的齿槽转矩Tcog作为响应,槽口偏移角度β和槽口宽度λ作为自变量,目标函数定义为
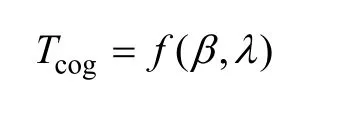

通过响应面法优化过程,可以得到使无刷直流电机齿槽转矩Tcog最小的β和λ值。
图5 给出了响应面优化齿槽转矩的流程图。首先,根据自变量和响应设计试验,本文采用有限元法建立无刷直流电机模型进行试验,需要注意的是,各自变量的上下限选择一定要合理,并且包含最优解,本文槽口偏移角度β的范围为0°~6°,为获取相对准确的数学模型,选取 2.6°<β<3°、2mm<λ<3mm 作为自变量β和λ的上下限。然后,对试验结果进行统计分析,验证所得数学模型的合理性。表2 为对FEM 试验进行统计分析后得到的几个反应数学模型合理性的系数。
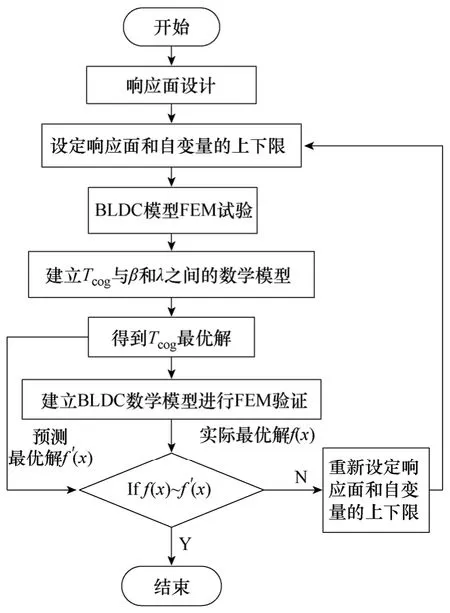
图5 响应面优化流程图Fig.5 Optimization steps of RSM
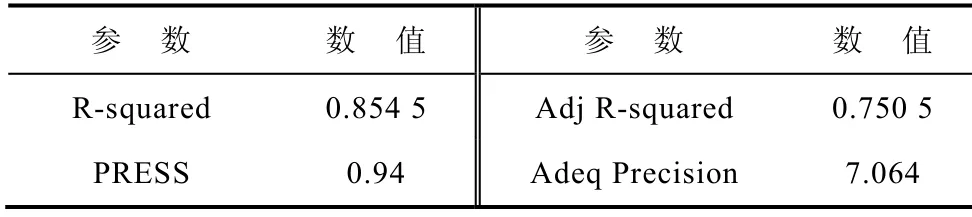
表2 RSM 齿槽转矩分析结果Tab.2 The cogging torque analysis results using RSM
下面,对表2 中的几个系数进行分析,验证数学模型的合理性。
R-squared=0.854 5。判定系数R-squared 代表的是响应面与真实值之间的差异程度,取值范围为0~1,该系数越大,差异程度越小,当R-squared=1时,表示二者完全一致。该数学模型的R-squared=0.854 5,较为理想。
Adj R-squared=0.750 5。由于R-squared 具有一定的局限性,因此需要进一步验证校正判定系数Adj R-squared。如果向模型中添加的变量没有统计学意义,则 Adj R-squared 会减小。因此 Adj R-squared的值越大,模型拟合的越好。
PRESS=0.94。参数PRESS 能够反应模型预测新数据的准确程度,该参数的值越小,表明预测新数据的准确性越高。
Adeq Precision=7.064。Adeq Precision 是反应信噪比的参数,取值应大于4,该模型Adeq Precision的值为7.064,较为合理。
最终得到Tcog与β和λ之间的数学模型为
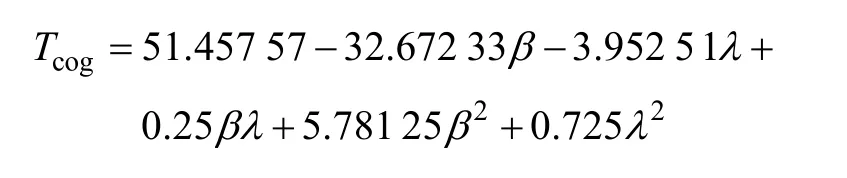
齿槽转矩Tcog与槽口偏移角度β、槽口宽度λ的响应面如图6 所示。最优槽口偏移角度β和槽口宽度λ组合见表3。
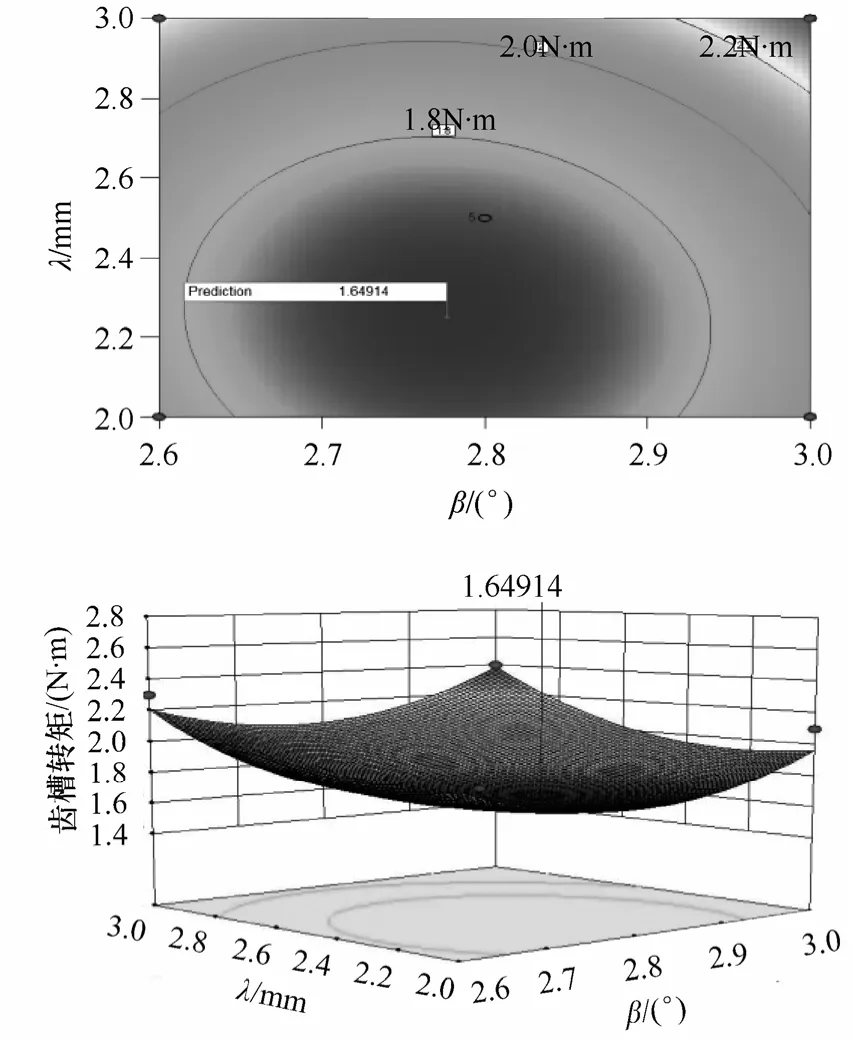
图6 齿槽转矩与β 和λ的响应面Fig.6 Response surface plot of cogging torque in term of β and λ

表3 最优槽口偏移角度和槽口宽度组合Tab.3 The optimum combination of β and λ
4 优化结果验证
取槽口偏移角度β=2.78、λ=2.25 建立无刷直流电机二维模型进行有限元分析,仿真结果得到齿槽转矩Tcog=1.61N·m,与预测结果之间的误差仅为2.365%(见表4)。为了与文献[15]中所提出的槽口偏移方法进行对比,采用文献[15]中所提出的槽口偏移方法重新建立电机模型,并应用与前面相同的优化过程得出最优结果,图7 为最终得到的几种齿槽转矩的波形对比,由图可以看出,初始电机的齿槽转矩幅值约为13N·m,采用文献[15]中的优化方法齿槽转矩的幅值减为3.75N·m,齿槽转矩削弱了约71.2%,而采用本文的优化方法齿槽转矩幅值减小为1.61N·m,齿槽转矩削弱了约87.6%,因此本文所采用的优化槽口偏移角度和槽口宽度方法对齿槽转矩的削弱效果更为明显。

表4 FEM 验证结果Tab.4 Validation results using FEM
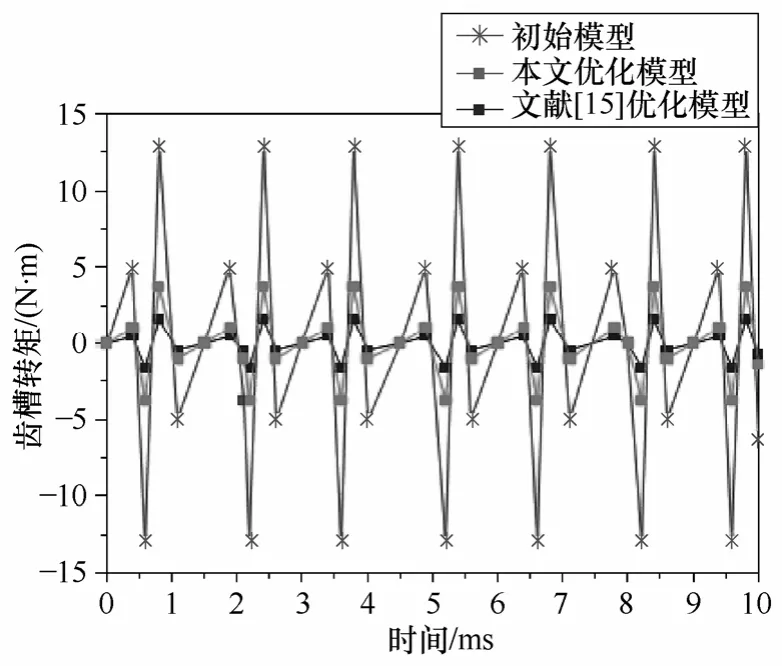
图7 β=2.78、λ=2.25 与电机初始模型以及文献[15]中 偏移模型齿槽转矩对比Fig.7 The comparison of cogging torque between initial model and optimum model when β=2.78、λ=2.25 and the model in paper[15]
图8 对优化前后的大功率无刷直流电机反电动势波形进行了对比,由图可以看出,采用本文的方法抑制大功率无刷直流电机的齿槽转矩几乎不会对反电动势波形造成影响,反电动势仍为平顶宽度不小于120°的梯形波,效果较为理想。
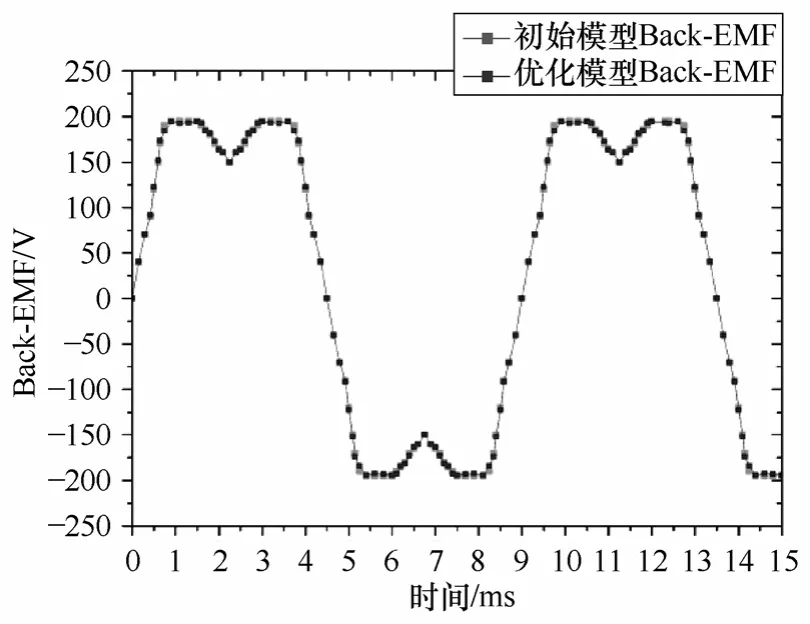
图8 β=2.78、λ=2.25 与初始电机反电动势波形对比Fig.8 The comparison of back EMF between initial model and optimum model when β=2.78、λ=2.25
5 结论
本文以电动汽车用大功率无刷直流电机作为研究对象,通过合理组合定子槽口偏移角度与槽口宽度抑制其齿槽转矩,应用响应面法寻求槽口偏移角度和槽口宽度的最优组合。最终得到当槽口偏移角度β=2.78、槽口宽度λ=2.25 时,齿槽转矩削弱效果最为明显。仿真结果表明,无刷直流电机的齿槽转矩削弱了约87.6%,并且反电动势波形未被破坏,仍为平顶宽度不小于120°的梯形波。因此采用本文所提出的方法能够有效减小电动汽车的低速转矩脉动,提高电动汽车性能。
[1]刘刚,王志强,房建成.永磁无刷直流电机控制技术与应用[M].北京:机械工业出版社,2008.
[2]Hendershot J R,Miller T J E.Design of brushless permanent magnet motors[M].Oxford,UK:Clarendon,1994.
[3]Abbaszadeh K,Rezaee Alam F,Saied S A.Cogging torque optimization in surface-mounted permanent-magnet motors by using design of experiment[J].Energy Conversion and Management,2011,52(10):3075-3082.
[4]Kyu Yun Hwang,Sang Bong Rhee,Byoung Yul Yang,et al.Rotor pole design in spoke-type brushless DC motor by response surface method[J].IEEE Transactions on Magnetics,2007,43(4):1833-1836.
[5]Luksniszin A,Jagiela A,Wrobel R.Optimization of permanent magnet shape forminimum cogging torque using a genetical gorithm[J].IEEE Transactions on Magnetics ,2004,40(2):228-1231.
[6]杨玉波,王秀和,丁婷婷,等.极弧系数组合优化的永磁电机齿槽转矩削弱方法[J].中国电机工程学报,2007,27(2):7-11.Yang Yubo,Wang Xiuhe,Ding Tingting,et al.Analysis of the optimization of the pole arc combination to reduce the cogging torque in PM motors[J].Proceedings of the CSEE,2007,27(2):7-11.
[7]程树康,葛新,高宏伟,等.分数槽无刷直流电动机齿槽定位力矩的研究[J].中国电机工程学报,2008,28(21):107-111.Cheng Shukang,Ge Xin,Gao Hongwei,et al.Research of cogging torque in the brushless DC motor with fractional ratio of slots and poles[J].Proceedings of the CSEE,2008,28(21):107-111.
[8]王道涵,王秀和,丁婷婷,等.基于磁极不对称角度优化的内置式永磁无刷直流电动机齿槽转矩削弱方法[J].中国电机工程学报,2008,28(9):66-70.Wang Daohan,Wang Xiuhe,Ding Tingting,et al.Optimization for the asymmetric angles of magnetic pole to reduce cogging torque in inner-buried PM brushless DC motors[J].Proceedings of the CSEE,2008,28(9):66-70.
[9]Kyu Yun Hwang,Hai Lin,Se Hyun Rhyu,et al.A study on the novel coefficient modeling for a skewed permanent magnet and overhang structure for optimal design of brushless DC motor[J].IEEE Transactions on Magnetics,2012,48(5):1918-1923.
[10]Islam R,Husain I,Fardoun A,et al.Permanent magnet synchronous motor magnet designs with skewing for torque ripple and cogging torque reduction[J].IEEE Transactions on Industry Applications,2009,45(1):152-160.
[11]Yang Yubo,Wang Xiuhe,Zhang Rong,et al.The optimization of pole arc coefficient to reduce cogging torque in surfacemounted permanent magnet motors[J].IEEE Transactions on Magnetics,2006,42(4):1135-1138.
[12]谭建成.永磁无刷直流电机技术[M].北京:机械工业出版社,2011.
[13]王秀和.永磁电机[M].北京:中国电力出版社,2007.
[14]王秀和,杨玉波,等.基于极弧系数选择的实心转子永磁同步电动机齿槽转矩削弱方法研究[J].中国电机工程学报,2005,15(8):146-149.Wang Xiuhe,Yang Yubo,et al.The method for reducing cogging torque by suitable selection of pole-arc coefficient in solid-rotor PM synchronous motors[J].Proceedings of the CSEE,2005,15(8):146-149.
[15]Karim Abbaszadeh,MostafaJafari.Optimizing cogging torque reduction in slot opening shift method for BLDC motor by RSM[C].Power Electronics,Drive Systems and Technologies Conference(PEDSTC),2011,2:62-66.
[16]Abbaszadeh K,Rezaee Alam F,Teshnehlab M.Slot opening optimization of surface mounted permanent magnet motor for cogging torque reduction[J].Energy Conversion and Management,2012,55(10):108-115.
