地铁牵引变流器-电机系统稳定性控制
2013-07-06赵雷廷刁利军刘志刚
赵雷廷 刁利军 董 侃 刘志刚
(北京交通大学电气工程学院 北京 100044)
1 引言
牵引变流器-电机系统是地铁车辆的动力来源,由直流接触网、滤波器(滤波电感与支撑电容)、牵引变流器、牵引电机等组成[1,2]。鉴于运营的实际需求,多车辆同时启动或者制动的情况时有发生,而且随着近年来四象限变流器等吸收装置在供电系统中的引入[3],一旦供电系统控制参数设计与当前实际运营数据不匹配,则很容易引起直流网侧电压波动;与此同时,直流侧滤波电感及支撑电容受到车载变流装置本身空间、重量以及谐波抑制要求等诸多因素限制,参数的选择通常为较大的电感、较小的电容,且为了避免能量的过多损耗,线路电阻与电感内阻之和也不宜设计过大,因此系统阻尼系数较小[4];而牵引变流器在矢量控制策略下呈现负阻抗特性[5],导致系统阻尼系数再次减小,从而引发牵引传动系统直流侧电压、电流持续振荡,电机输出转矩脉动,严重时则会产生过压、过流故障保护,牵引变流器封锁脉冲,系统丧失牵引力。
为确保地铁车辆的安全稳定运行,“输入滤波器-牵引变流器-异步电机”的整体系统稳定性研究已经逐渐成为业界研究的重要方向之一,SIEMENS、Bombardier、ALSTOM 等国外厂商针对上述问题已经展开了细致的分析并提出了一些相关的解决措施[6-8],这些措施都以完美的转矩控制为前提,在系统运行的某一工作点附近利用小信号分析法将牵引变流器等效为一个恒定的阻抗[9],然而牵引传动系统在实际的运行过程中,由于受到磁链观测误差、A-D 采样误差、谐波干扰以及系统时延等因素的影响,完美的转矩控制是不可能真正实现的,因此恒定的阻抗并不能用来准确且全面地分析系统的稳定性[10]。
本文通过建立牵引传动系统线性化结构图、异步电机Γ形等效电路以及转子磁场定向矢量控制近似线性化模型,从而得到牵引变流器输入导纳线性化模型,在此基础上针对整个系统的稳定性进行分析,阐释系统的振荡机理并提出一种新型稳定性控制器以获得理想的牵引变流器输入导纳,从而抑制系统振荡,提高系统稳定性。
2 牵引传动系统结构
图1 所示为地铁牵引传动系统框图。直流接触网通过输入滤波器向牵引变流器提供 1 500V 或750V 直流电,转矩控制系统采集直流侧电压Ud、电机定子三相电流ia、ib、ic以及电机机械转速ωm,采用转子磁场定向矢量控制,输出三相变频变压交流电以驱动异步电机运行。
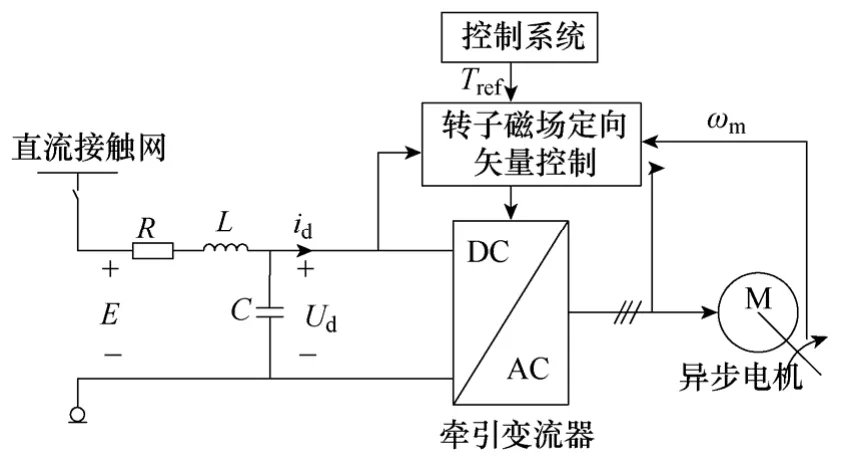
图1 地铁牵引传动系统框图Fig.1 Schematic of metro drive system
图1 中,R为线路电阻与电感内阻之和,L为滤波电感,C为支撑电容。系统直流侧电压通过牵引变流器影响直流侧电流,在完美的转矩控制前提下牵引变流器可以被等效为一恒定阻抗,而本文基于实际的运行情况将牵引变流器等效为一非线性函数
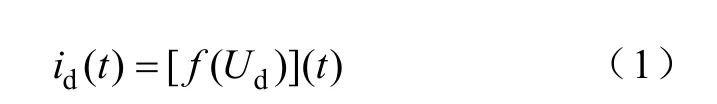
从而定义牵引变流器线性化输入导纳为

如果将直流网侧电压与直流侧电流作为牵引传动系统的输入,直流侧电压作为系统输出,则系统输入滤波器频域下方程为
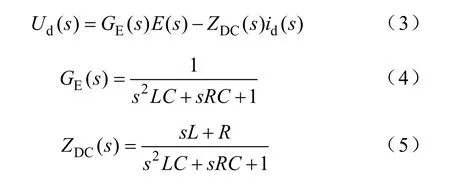
结合式(2)最终可以得到牵引传动系统线性化结构图如图2 所示,继而将系统稳定性的分析归结于对牵引变流器线性化导纳模型的分析。
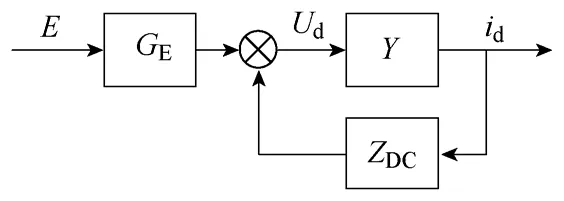
图2 牵引传动系统线性化结构图Fig.2 Linear feedback model of drive system
3 系统稳定性分析
3.1 牵引变流器线性化导纳模型建立
这里通过建立异步电机数学等效模型、变流器脉宽调制策略以及转子磁场定向矢量控制的近似线性化模型,最终得到牵引变流器输入导纳线性化模型。结合上文所述系统直流侧滤波器模型,对牵引传动系统的整体稳定性进行分析。
建立图3 所示考虑漏感的异步电机Γ形等效电路图,其特点是定子漏感为0,LM=Ls即等效励磁磁链ψM等于实际的定子磁链ψs[11]。Rs和RR分别为电机定子电阻和等效转子电阻,Lσ则表示电机等效漏感,rψ′为转子磁链。
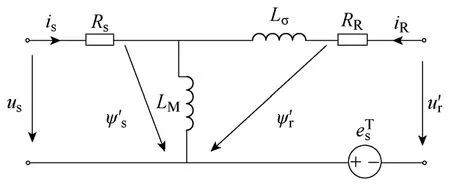
图3 异步电机Γ形等效电路Fig.3 Γ-equivalent circuit of induction motor
根据Γ形等效电路建立异步电机在同步旋转坐标系下采用转子磁场定向矢量控制的数学模型
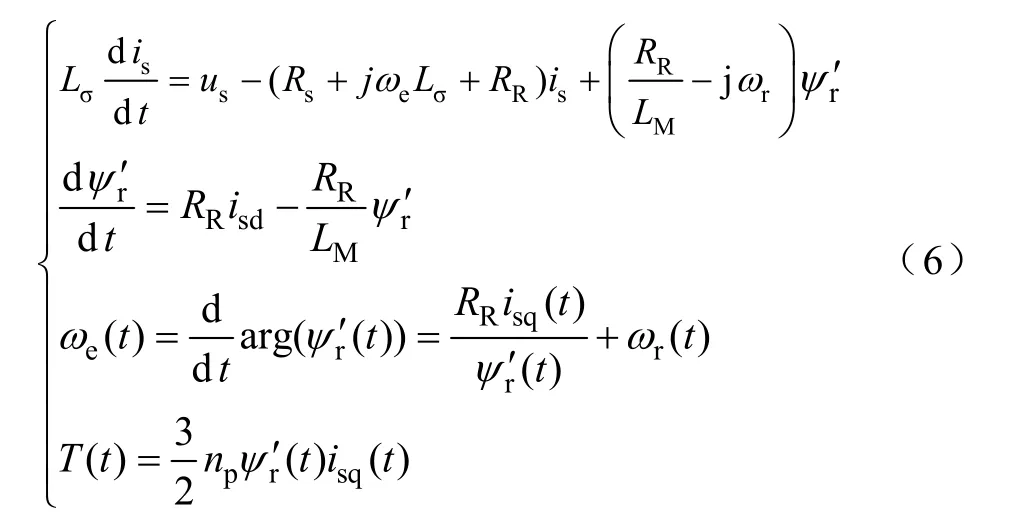
式中
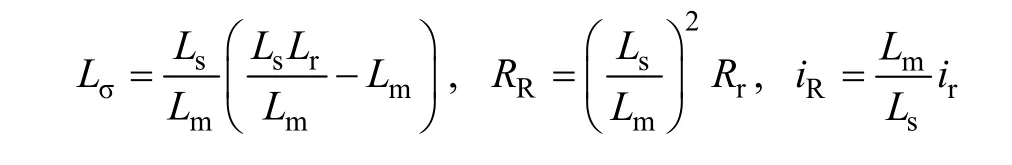
同时牵引变流器采用PWM 脉宽调制策略,在当前开关周期内将直流电压转变为与控制系统给定电压值相等的可变频变压三相电机定子交流电压以驱动异步电机运行,电机定子电压us模型如下所示

为补偿直流侧电压波动的影响,表征PWM 脉宽调制策略等效函数的k(t)被定义为

式中,usref为控制系统给定电机定子电压值;Ud上标横线表示其在一个开关周期内的平均值。
通过使用小信号模型分析法将式(8)线性化,可得
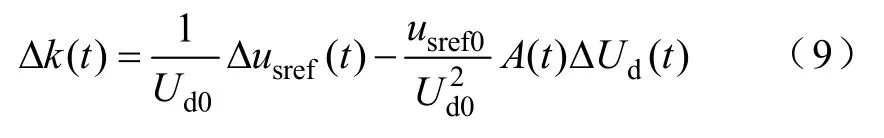
下标0 表示对应变量稳态值,A(t)为开关周期内求解平均值函数,结合式(7)最终可获得电机定子电压线性化模型为
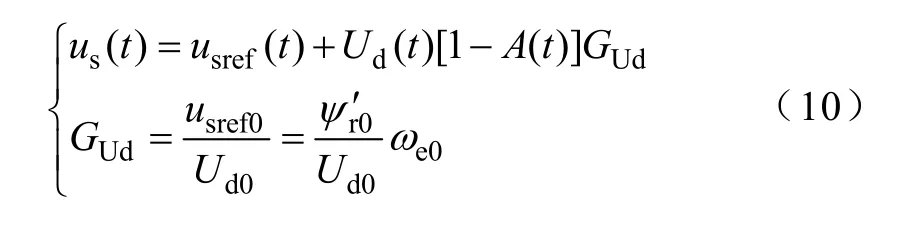
为消除异步电机等效模型由静止坐标系转换到旋转坐标系时所产生的耦合分量jωeLσ,控制系统采用反馈解耦策略[12],将电流控制器与异步电机模型所建立的开环传递函数开环极点在旋转坐标系下从-R/Lσ-jωe转移到-R/Lσ,进而通过选择适当的电流控制器PI 参数实现零极点对消,提高系统动态响应,最终使电流控制的特性独立于同步频率的变化。与此同时考虑到异步电机反馈电动势的存在,增加主动阻尼系数Ra以提高系统的抗干扰能力[13],电流控制器与异步电机系统结构图如图4 所示。
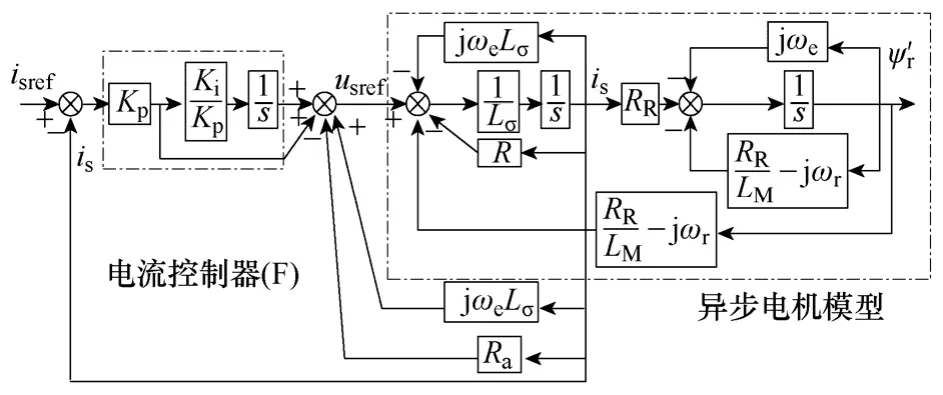
图4 电流PI 控制器与异步电机系统结构图Fig.4 Representation of the induction motor with PI current regulation
根据图4,电机定子电压给定值的表达式如下
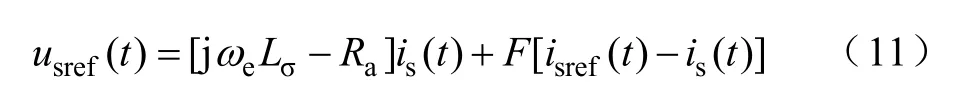
式中
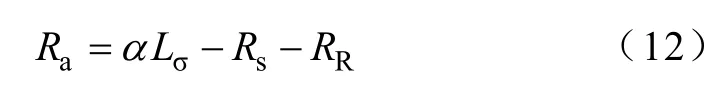
将反馈解耦以及主动阻尼系数与异步电机模型合并,得到电机定子电流转矩分量闭环控制系统框图如图5 所示。
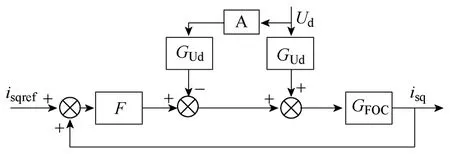
图5 电流转矩分量闭环控制系统Fig.5 Closed-loop control system of quadrature current
从而得到基于转子磁场定向控制的牵引传动系统近似线性化模型
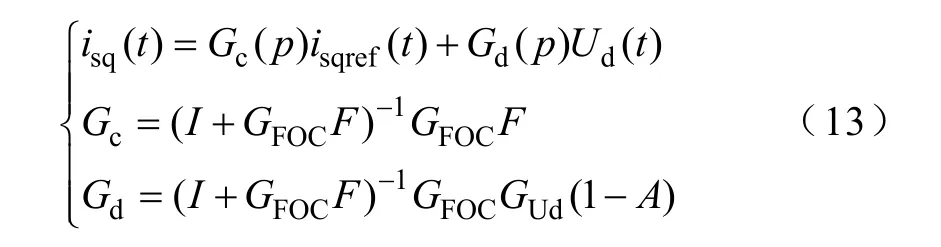
综合式(4)和式(5)建立输入滤波器-牵引变流器-异步电机的综合线性化模型如图6a 所示,电机定子电流转矩分量给定值和网侧电压作为系统输入,电机输出转矩以及直流侧电流作为系统输出。图中阴影部分形成的反馈回路在实际运行过程中即使在系统内部转矩控制良好的情况下也会产生不稳定现象。为简化反馈回路结构,引入上文所述牵引变流器输入导纳,得到图6b。
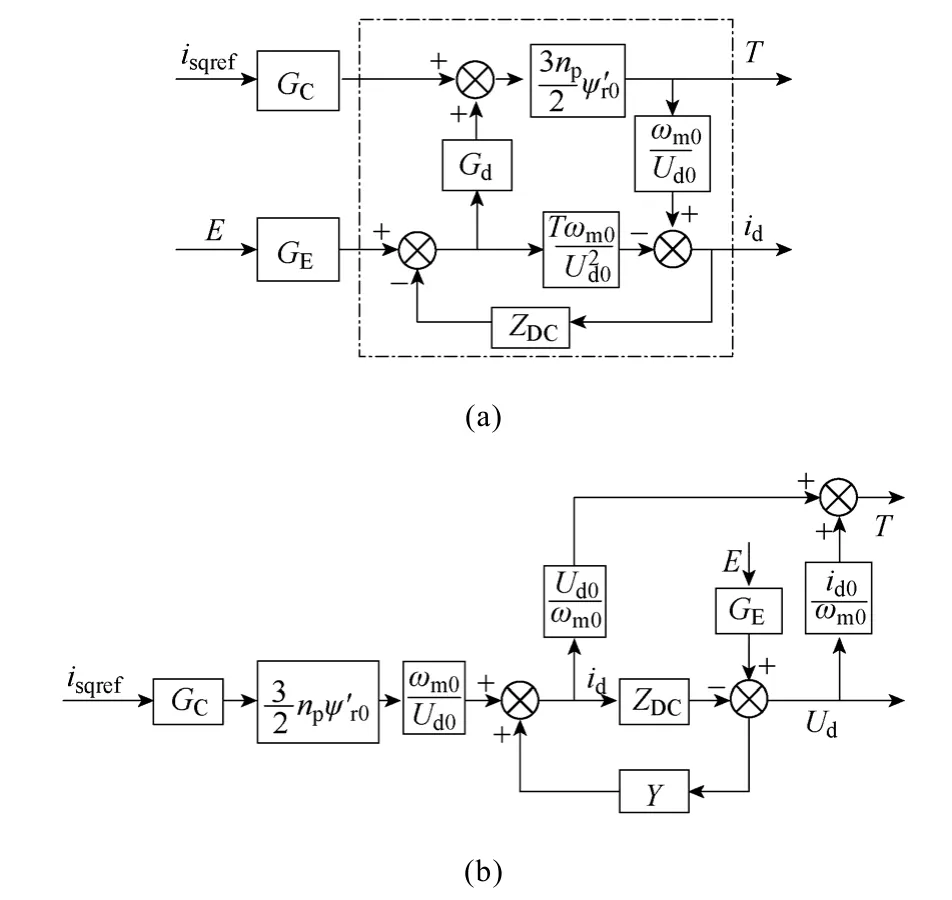
图6 系统综合线性化模型Fig.6 Comprehensive linear model of drive system
根据图6b 最终得到牵引变流器输入导纳线性化模型以及电机输出转矩、直流侧电压、电流线性化表达式如下所示

3.2 直流侧振荡产生机理
在传递函数GC、Gd以及变流器输入线性化导纳Y自身稳定的前提下,牵引传动系统整体稳定性取决于开环传递函数YZDC。由于系统输入滤波器ZDC阻尼系数较小,因此在谐振频率ω0附近其对数幅频曲线有较大的尖峰,同时相角从90°突变至-90°,如果此时线性化输入导纳Y等效为复频域下一向量,当 Re{Y(ω0)}<0 时,arg(YZDC(ω))必然穿越(2k+1)180°(k=0、±1、±2…),如图7 所示。
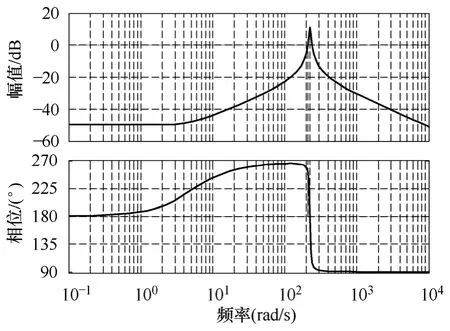
图7 开环传递函数YZDC Bode 图Fig.7 Bode diagram of open-loop transfer function YZDC
图7 为系统在直流侧电压1500V,滤波电感5.2mH,支撑电容 8.6mF,线路电阻与电感内阻之和34.8mΩ,电机等效漏感2mH,额定励磁电流60A条件下的开环传递函数YZDC频率域稳定分析仿真结果,在幅频特性曲线大于0的频率范围之内相频特性曲线穿越180°一次,根据奈奎斯特对数频率稳定判据可知此时系统处于不稳定状态,整个系统将产生持续振荡。
为抑制系统振荡,提高稳定性,则需要线性化导纳在复频域下相角始终处于90°到-90°之间,至少在输入滤波器谐振频率附近满足上述条件,因此如何获得理想的变流器输入导纳成为了系统稳定性设计的关键。
4 系统稳定性控制器设计
由于系统稳定性依赖于理想变流器输入导纳线性化模型。因此本文通过设计稳定性控制器在线修正电机定子电流转矩分量给定值,以获得最终的理想导纳模型,修正公式如下:
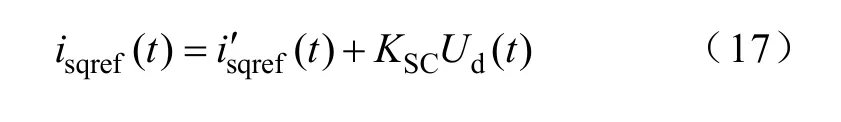
式中,KSC为稳定性控制器。
结合式(14)可以得到
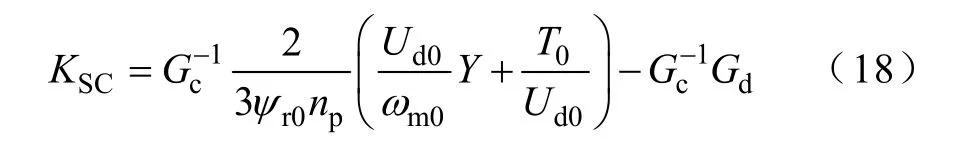
在(1-A(s))≈sTa的条件下,Ta为开关周期内平均值传递函数等效时间,则式(18)转化为
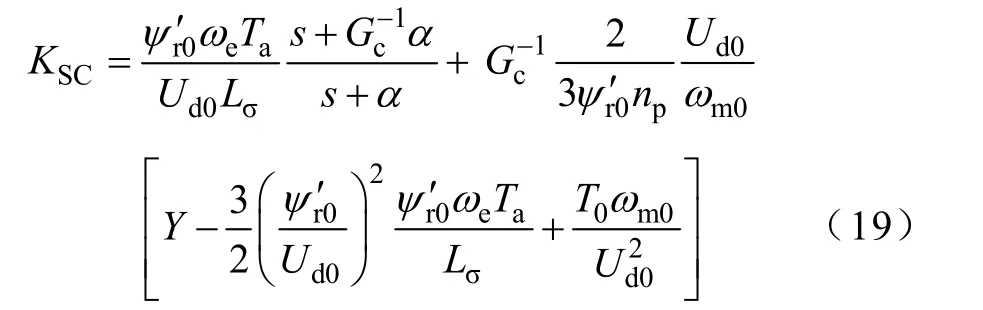
为使系统稳定并且具有最大的稳定裕度,理想的变流器输入导纳线性化模型在复频域下应为一具有正实部且虚部为0的矢量[14]为
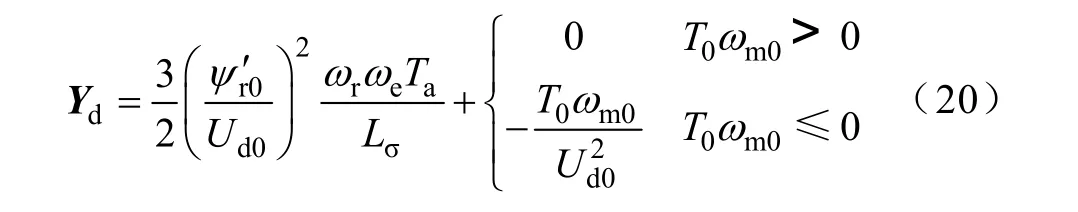
在牵引变流器等效为上述理想线性化输入导纳的条件下,整个牵引传动系统Bode 图如图8 所示。
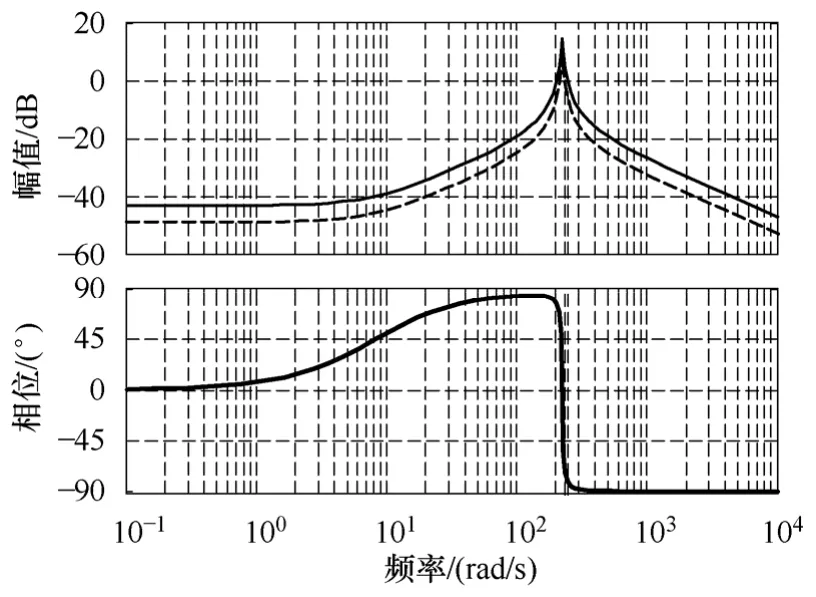
图8 理想线性化输入导纳下的开环 传递函数YdZDC Bode 图Fig.8 Bode diagram of open-loop transfer function YdZDC with ideal linear input admittance model
图8 中实线与虚线分别为系统在牵引工况以及制动工况下的对数幅相曲线,与图7 相比,理想变流器输入导纳线性化模型使系统开环传递函数YdZDC在车辆运行的任何工况下其相角都维持在 90°~-90°之间,从而使得系统处于稳定状态。
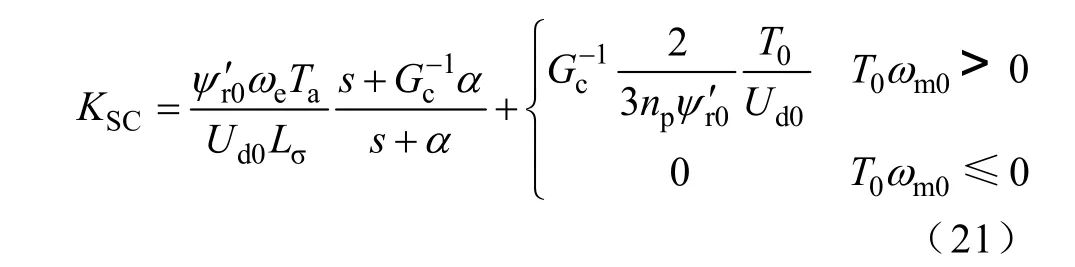
将理想变流器输入导纳线性化模型代入式(19)得 用滤波器Fl[6]代替式(21)第二项中的,同时将
为获得稳定性控制器KSC的精确数学模型,使 第一项中的近似等于 0.5,损失一定的稳定裕 度,以降低直流侧电压波动对电机输出转矩的影响,因此可以得到稳定性控制器最终模型为
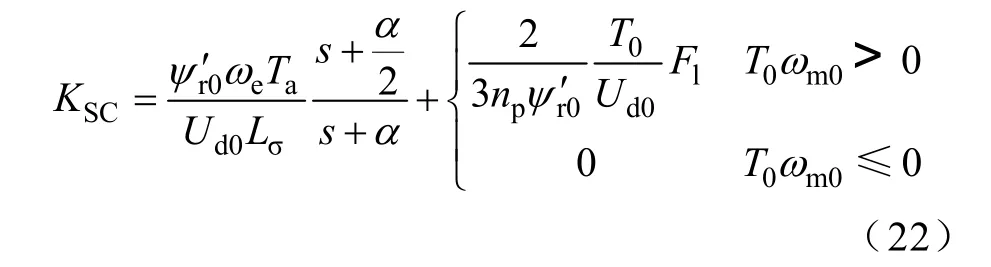
图9 给出了采用稳定性控制器与未采用稳定性控制器牵引传动系统运行时主要变量的仿真波形对比。其中包括电机转速n、电机输出转矩T、直流侧电压Ud以及网侧直流电流ig。
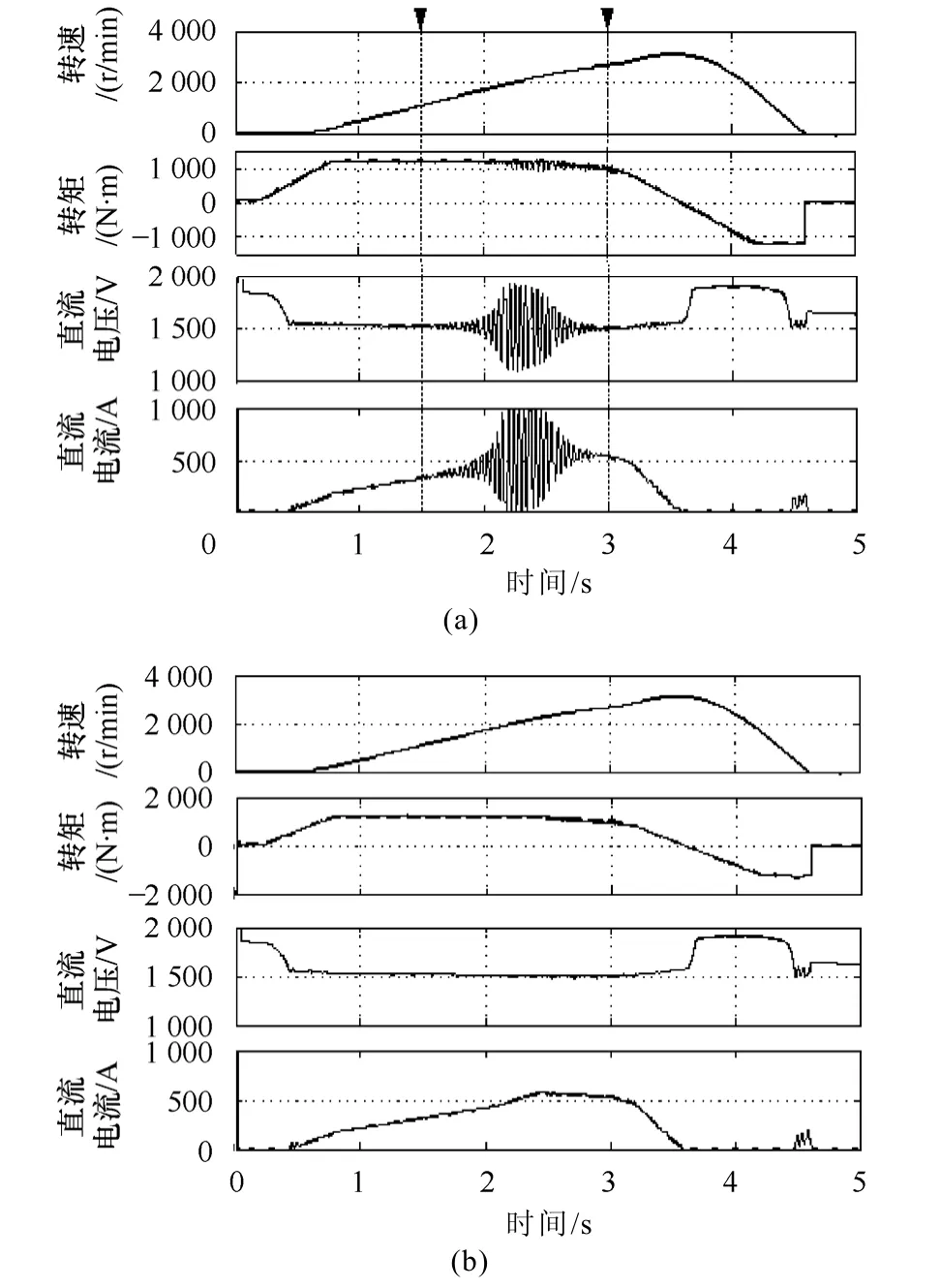
图9 牵引传动系统运行仿真图Fig.9 Simulation of drive system
从对比中可以看出系统采用稳定性控制器之后,牵引变流器在电机转速从0 上升至3 300r/min,运行工况由牵引→惰性→制动的过程中,消除了系统振荡现象,直流侧电压、网侧直流电流以及电机输出转矩变化平稳。
5 实验验证
图10 所示为自主开发研制的地铁A 型车牵引变流器。其直流侧线路电压1 500V,输入电流500A,额定容量1 000kVA,输出频率0~112Hz。为验证上述理论的正确性,本文进行了相关实验。

图10 地铁牵引变流器实物图Fig.10 Metro traction convertor
图11 为系统未采用稳定性控制器时,车辆在牵引工况下加速过程中,变流器直流侧以及电机振荡的波形图。其中包括同一变流器两并联电机交流侧电流和ia、网侧直流电流ig、直流侧电压Ud以及车速vp。从图中可以看出,车辆在AW0 载荷下,电机首先运行于恒转矩区,其输出转矩经过箱体温度、车辆载荷、防滑/防空转以及电机特性曲线等限制模块之后最终基本维持在1 000Nm。随着地铁车辆的速度增加,牵引变流器输出功率逐渐上升。当速度达到25km/h 左右,功率大约为220kW 时,牵引变流器直流侧电压、网侧直流电流、交流侧电流以及电机输出电流都出现持续振荡现象,直到车辆运行至30km/h 时,进入惰性工况。

图11 牵引传动系统直流侧和电机侧振荡波形Fig.11 The oscillation of traction drive system on the traction condition
图12 所示则为系统加入稳定性控制器之后,变流器直流侧电压,网侧直流电流以及电机输出电流波形图。随着车辆速度增加至25km/h 左右进入惰性工况,以及之后再次加速至55km/h的整个过程中,系统振荡得到了抑制,地铁车辆稳定运行。从而验证了上文所述稳定性控制器的正确性和有效性。
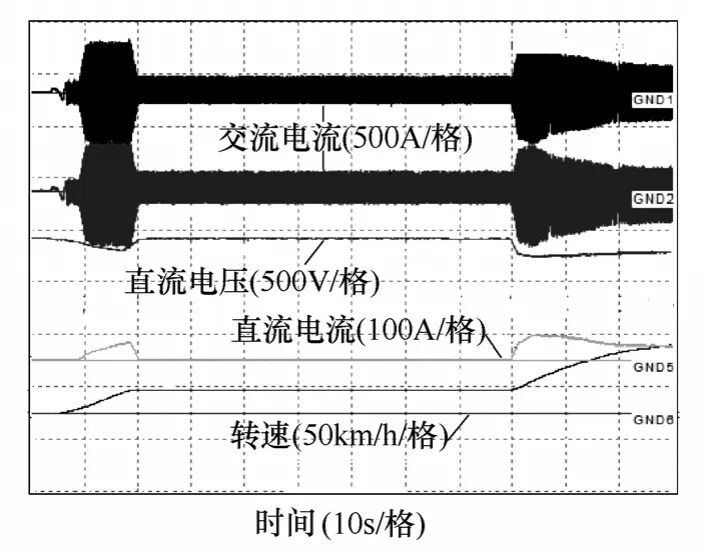
图12 牵引传动系统稳定运行波形Fig.12 Stable operation of traction drive system
6 结论
本文将直流侧输入滤波器以及牵引变流器控制策略相结合,分析了地铁牵引变流器-电机系统的整体稳定性。通过建立异步电机Γ 形等效电路以及转子磁场定向矢量控制的近似线性化模型从而得到了变流器输入导纳线性化模型,利用奈奎斯特对数频率稳定判据阐释了系统振荡的机理。在此基础上提出了一种以获得理想变流器输入导纳为目的的系统稳定性控制器,并给出其精确模型。模型仿真以及现场的实验都证明了该控制器的正确性和有效性,成功解决了牵引传动系统振荡的问题,确保了地铁车辆的安全稳定运行。
[1]孙大南.地铁车辆牵引电传动系统关键技术研究[D].北京:北京交通大学,2012.
[2]陈晓丽,何林娜.城市轨道交通车辆交流传动系统建模与仿真分析[J].城市轨道交通研究,2011(10):33-36.Chen Xiaoli,He Linna.Modeling and simulation of AC traction system for urban railway vehicles[J].Urban Rail Transit Research,2011(10):33-36.
[3]孔嵩.地铁能馈式牵引供电变流系统谐波分析及抑制研究[D].北京:北京交通大学,2011.
[4]Mosskull Henrik,Galic Johann,Wahlberg Bo.Stabilization of induction motor drives with poorly damped input filters[J].IEEE Transactions on Industrial Electronics,2007,54(5):2724-2734.
[5]Pietilainen Kai,Harnefors Lennart,Petersson Andreas,et al.DC-link stabilization and voltage sag ride-through of inverter drives[J].IEEE Transactions on Industrial Electronics,2006,53(4):1261-1268.
[6]Bae B H,Cho B H,Sul S K.Damping control strategy for the vector controlled traction drive[C].European Conference on Power Electronics and Applications,Graz,2001.
[7]Delemontey B,Iung C,Fornel B De,et al.Nonlinear decoupling of an induction motor drive with input filter[C].IEEE Conference on Control Applications,USA,1995:1004-1009.
[8]Delemontey B,Iung C,Fornel B De,et al.Stability analysis and stabilization of an induction motor drive with input filter[C].European Conference on Power Electronics and Applications,Spain,1995:2724-2734.
[9]孙大南,刘志刚,林文立,等.地铁牵引变流器直流侧振荡抑制策略研究[J].铁道学报,2011,33(8):52-57.Sun Danan,Liu Zhigang,Lin Wenli,et al.Research on DC-link oscillation suppression strategy in metro traction convertor[J].Journal of the China Railway Society,2011,33(8):52-57.
[10]Henrik Mosskull.Stabilization of an induction machine drive[D].Sweden:Royal Institute of Technology,2003.
[11]Lennart Harnefors,Kai Pietilainen,Lars Gertmar.Torque-maximizing field-weakening control:design,analysis,and parameter selection[J].IEEE Transactions on Industrial Electronics,2001,48(1):161-168.
[12]Fernando Briz,Michael W Degner,Robert D Lorenz.Analysis and design of current regulators using complex vectors[J].IEEE Transactions on Industry Applications,2000,36(3):817-825.
[13]Fernando Briz del Blanco,Michael W.Dynamic analysis of current regulators for AC motors using complex vectors[J].IEEE Transactions on Industrial Electronics,1999,35(6):1424-1432.
[14]Henrik Mosskull.Stabilization of an induction motor drive with resonant input filter[C].Power Electronics and Applications,2005:10pp.-p.10.
