基于CFD的自进式喷嘴参数优化

王常斌 王 敏 徐 洋 魏 巍

（东北石油大学，黑龙江大庆 163318）

基于CFD的自进式喷嘴参数优化

王常斌 王 敏 徐 洋 魏 巍

（东北石油大学，黑龙江大庆 163318）

为了有效穿透井眼污染带，扩大泄油面积，提高油藏采收率，最终实现增产增注的目的。通过建立喷嘴三维模型，采用Fluent软件进行模拟，研究自进式喷头在不同前后喷嘴直径、前后喷嘴角度下的流场特性，利用流场中速度的分布规律结合公式计算出反冲力、破岩力、推进力的变化趋势。结果表明：随着后喷射角直径和前喷射角角度的增大，反冲力、推进力增大，破岩力减小；随着前喷射角直径和后喷射角度的增大，反冲力和推进力减小，破岩力增大。最终得到喷嘴的匹配方案，为实际生产提供了可靠依据。

水力喷射钻孔；高压水射流；自进式破岩；数值模拟

20世纪以来，水力喷射技术在油田中的应用越来越广泛［1-2］。目前，美国公司研制的JetDril射孔体系已经得到了较成熟的应用，但由于油藏特性和形态不同，还需要进一步改善［3-5］。国内自1994年始，在大庆、吐哈、辽河等油田进行了试验，但仍存在喷射距离短、近井带污染等缺点［6-8］。随着CFD软件的可靠性不断提高，利用计算机仿真研究水力喷射钻孔技术对实际应用有很大参考价值。因此，笔者应用Fluent软件模拟不同参数下的喷嘴喷射情况，从而建立起高效的喷嘴匹配方案。

1 数学模型

喷头喷射过程中的水射流示意图如图1所示。其中，后喷嘴喷射角度θ1，前喷嘴喷射角度θ2，后孔直径d1，前孔直径d2。喷头入口流量Q0为28 L/min，压力p为60 MPa，d2为0.4 mm，d1为0.5 mm，θ2为30°，θ1为55°，前后喷孔数量均为4个。

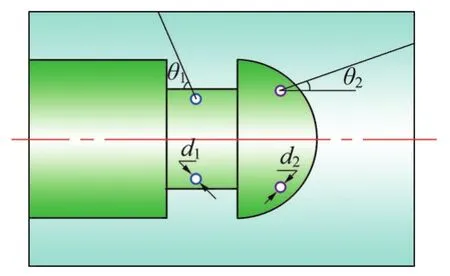
图1 喷头射流示意图

对连续射流，在喷嘴出口截面内外两点间应用伯努利方程，忽略两点间的高度差，可得出如下关系式［9］

式中，ρ1、ρ2分别为喷嘴内、外液体密度，kg/m3； p1、p2分别为喷嘴内、外静压力，MPa；v1、v2分别为内、外流体平均流速，m/s。

在两点间应用连续方程，并且A＝πd2/4，ρ1=ρ2，即可得出

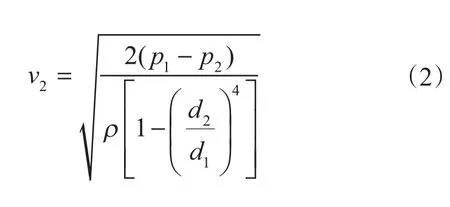
由于p1＞＞p2，（d2/d1）4＜＜1，同时将ρ=998 kg/m3代入式（2），得出射流流速

式中，v为射流流速，m/s；p为射流压力，MPa。

由q=vA计算出射流流量

式中，q为射流流量，L/min；d为喷嘴出口直径，mm。

在实际应用中，射流反冲力是一个基本参数。在喷嘴出口截面内外两点间应用动量定理［9］得

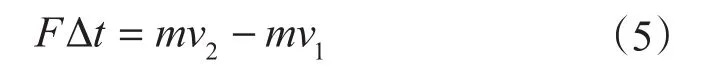
式中，F为单位时间内作用在单位体积流体上的力，N；Δt为作用时间，s；m为单位体积流体质量，kg；v1、v2分别为喷嘴出口截面内、外流体平均流速，m/s。

由作用力等于反作用力可知，上式中F的反值即为射流反冲力值Ff。考虑到m/Δt=ρq，在喷嘴出口截面内外两点间应用连续性方程，经推导后可得

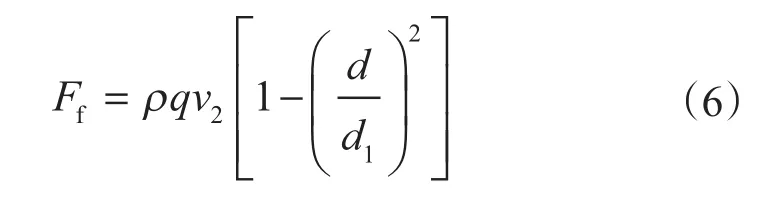
将式（3）代入式（6），得

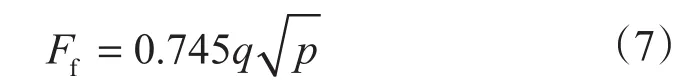
式中，Ff为水流反冲力，N。

将式（4）代入式（7），可得出射流反冲力的另一表达式［10］

对于本算例反冲力的表达式应为

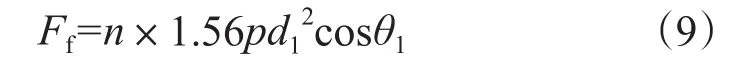
式中，n为喷嘴数量，个；θ1为后喷嘴喷射角度，°；d1为后喷嘴直径，mm。

对于本算例破岩力表达式

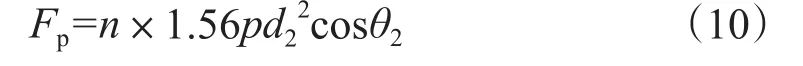
式中，Fp为水流破岩力，N；θ2为前喷嘴喷射角度，°；d2为前喷嘴直径，mm。

自进式喷头推进力等于反向喷嘴反冲力与破岩力之差，其表达式

式中，Ft为推进力，N。

2 数值模拟及分析

建立不同前、后喷嘴喷射角度和前、后喷嘴直径，以此得到流场的分布形态，并对流场进行分析，以了解射流流场特性，从而指导喷嘴设计。

三维模型的建立如图2所示，其中，前、后喷嘴各4个，喷头由两个圆柱体和一个半球形组成，圆柱形岩层高30 mm，底边直径20 mm，采用淹没射流。对整个模型进行网格划分，在Gambit中进行边界条件设置，指定连续类型后进行模拟计算，模拟过程中采用k-ξ湍流模型。

图2 模型的网格划分图

改变参数来模拟喷头喷射情况，经迭代、收敛后，分别创建XY平面，前喷孔平面和后喷孔平面，最终得到喷头各个平面速度云图见图3。

2.1 后喷孔直径

对同一喷嘴而言，随着喷嘴直径减小，喷孔最大速度会逐渐增大，射流能量也随之集中，破坏性能逐步增强，但破坏区域越来越小。在实际选择喷嘴直径时，往往要和进口压力匹配好。如果喷嘴直径过大，泵流量供应不足时，会导致喷射的水流不足，喷嘴破坏能力不够［11］，所以这里选择压力为60 MPa。前孔直径为0.40 mm、前喷角为30°、后喷角为55°时，改变后喷孔直径d1分别为0.50、0.55、0.60、0.65、0.70 mm，模拟后选取各喷射孔的最大速度，然后结合公式（9）、（10）和（11）。图4为模拟后的反冲力、破岩力和推进力随后喷射孔直径增加的变化图。

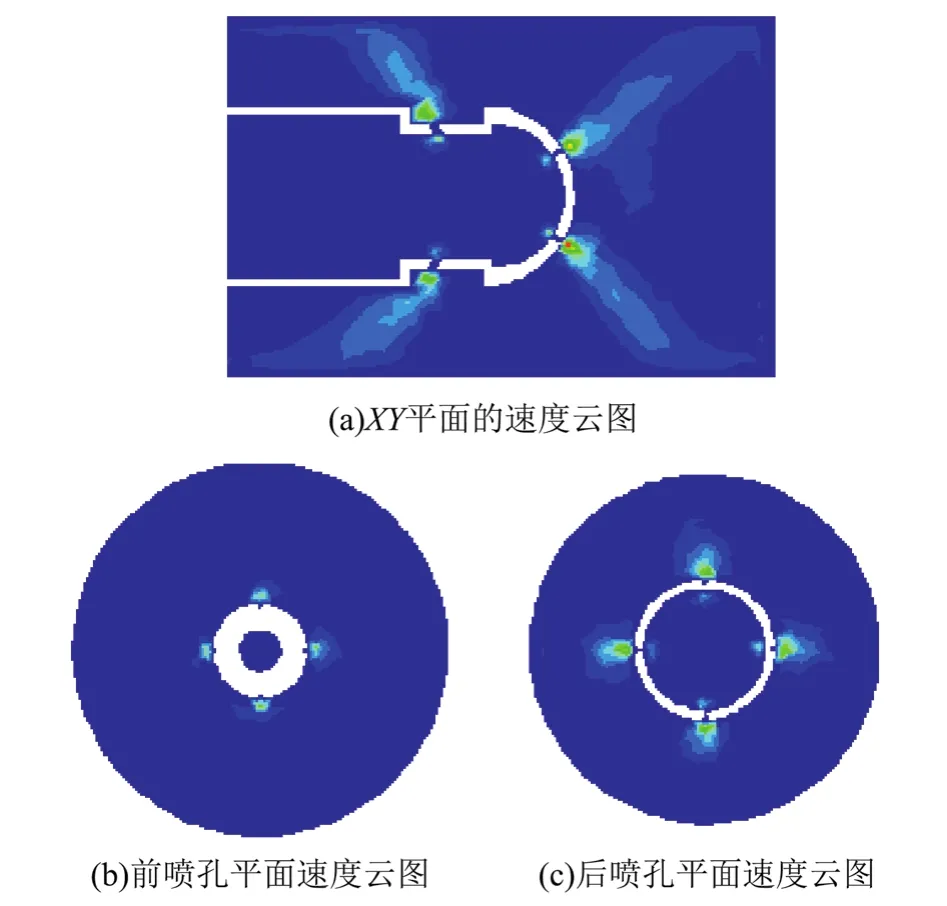
图3 模拟后不同平面的速度云图

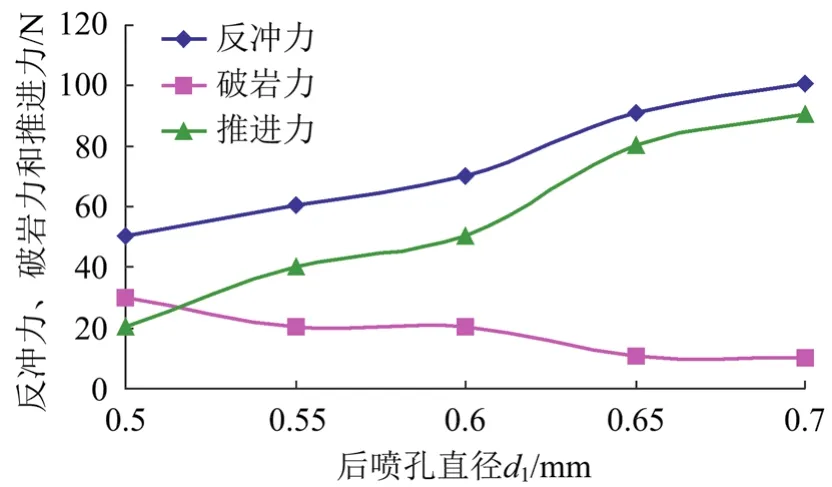
图4 3种力在不同后喷孔直径d1下的变化

由图4可知，随着后喷射孔直径d1的增大，反冲力整体趋势增大，而破岩力逐渐减小，这就导致推进力整体趋势增大，并且推进力增大趋势较大。为了使喷头作业效果达到最佳状态，且3种力都不至于太小，这里选择后喷射孔直径d1为0.55～0.65 mm之间比较合适。

2.2 前喷孔直径

选择后喷孔直径为0.7 mm、前喷角为30°、后喷角为55°，改变前喷孔直径d2分别为0.40、0.42、0.44、0.46、0.48 mm，计算出模拟后的3种力。图5为模拟后反冲力、破岩力和推进力随前喷孔直径增加的变化图，可以看出，随着前喷射孔直径d2的增大，反冲力呈减小趋势，破岩力呈增大趋势，导致推进力整体呈减小趋势。其中，反冲力和推进力的减小趋势较大。因此，为了使喷头达到较好的破岩效果，在这里选择前喷射孔直径d2在0.40～0.44 mm之间。

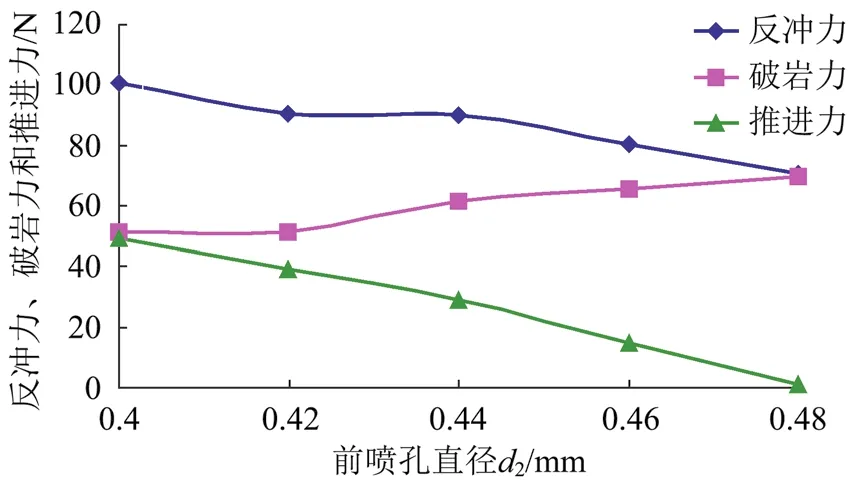
图5 3种力在不同前喷孔直径d2下的变化

2.3 后喷射孔角度

对于不同安装角度喷嘴，模拟结果相差很大［11］。并且，它对于喷射范围起着决定性的作用，因此，在模拟过程中，喷射角度会作为一个重要参数来优化。

建立前孔直径为0.40 mm、后孔直径为0.50 mm、前喷角为30°时，改变后喷角θ1分别为55°、60°、65°、70°，计算出模拟后的3种力。图6为模拟后反冲力、破岩力和推进力随后喷角的变化图。

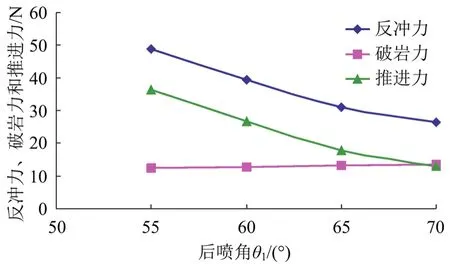
图6 不同后喷角θ1下3种力的变化

由图6可知，随着后喷角θ1的增大，反冲力呈减小趋势，破岩力呈增加趋势，推进力整体呈减小趋势，并且减小趋势较大，为了使喷头破岩和前进效果达到较高水平，3种力不宜过小，所以，这里选择后喷角θ1为55°～60°之间。

2.4 前喷射孔角度

选择前孔直径为0.40 mm、后孔直径为0.60 mm、后喷角为55°，改变前喷角θ2分别为5～60°，计算出模拟后3种力。图7为模拟后反冲力、破岩力和推进力随前喷角增大的变化图。

由图7可知，随着前喷角θ2增大，反冲力呈增大趋势，破岩力呈减小趋势，使推进力整体呈增大趋势。前喷嘴角度对射流结果有很大影响，如果角度过小，会出现喷头无法前进，达不到破岩目的。如果射流角度过大会出现喷射不到壁面，无法破岩，甚至堵塞孔道的现象，并且，为了使推进力较大的同时，破岩力又不至于太小，所以最终选择前喷角θ2在40°～50°之间。

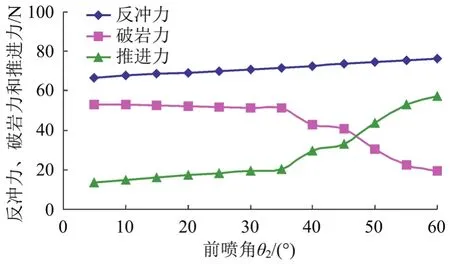
图7 不同前喷角θ2下3种力的变化

3 匹配方案

对于自进式喷头考虑的参数包括：前、后喷嘴直径和前、后喷嘴角度等。结合以上模拟及计算结果，得到的参数匹配方案，见表1。

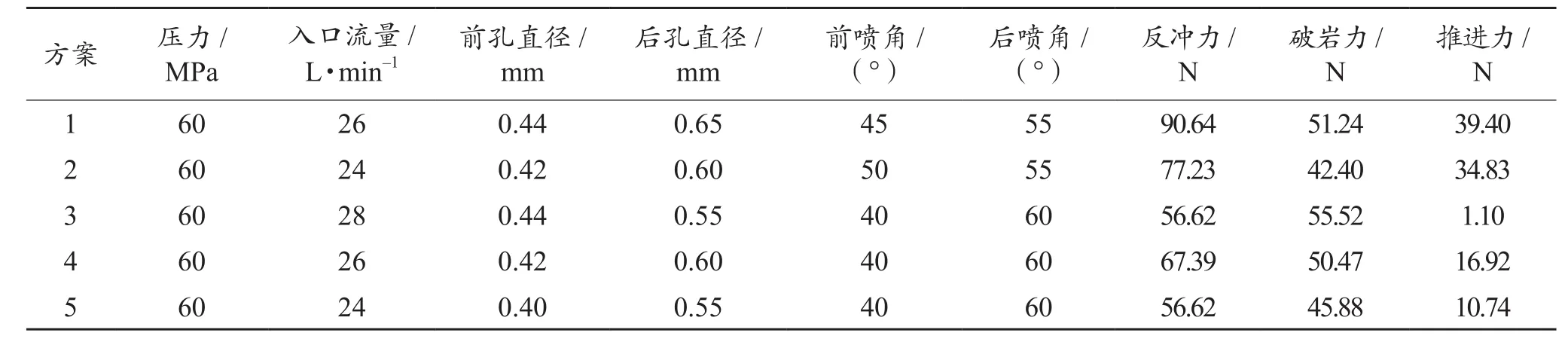
表1 喷嘴结构参数的匹配方案

以上方案在实际的生产运行中都是可以采用的，对于方案1、4、5，反冲力、破岩力和推进力大小适中，可以直接采用，但是，方案4、5推进力较小；对于方案2，它的破岩力相对较小，不利于破岩顺利进行；方案3的反冲力和破岩力虽然数值适中，但是推进力过小，不利于喷嘴自进。

4 结论

针对高压水射流技术的不足，模拟不同喷嘴喷射情况，并根据喷嘴参数制定匹配方案，得到以下结果：后喷孔直径增大，反冲力、推进力增大，加快水力喷射钻孔速度；前喷孔直径增大，破岩力增大，推进力减小，加速破岩效果；后喷嘴安装角度增大，反冲力、推进力随之减小，降低了钻孔速度；前喷嘴安装角度增大，破岩力减小，推进力增大，喷嘴自进性强。

［1］王步娥，舒晓晖，尚绪兰，等.水力喷射射孔技术研究与应用［J］.石油钻探技术，2005，33（3）：51-53.

［2］张继峰，罗文银.水力深穿透射孔技术在吐哈油田的应用前景［J］.吐哈油气，2002，7 （4）：362-367.

［3］LOVE R G, SHELTON R Q, MECALLAJ B, et al. Method and apparatus for perforating and slotting well flow conduetors ［P］. United States, 4134453.1979-0l-16.

［4］PITTMAN F C. Hydra-jet Tool ［P］.United States, 3145776.1964-08-25.

［5］SEHELLSTEDE J .Well penetration apparatus and method［P］.United States, 4640362.1987-02-03.

［6］孙龙勇.高压水射流深穿透水平射孔技术研究［D］.大连：大连理工大学，2010：3-4.

［7］王常斌，沈艳霞，刘照东，等.锥直喷嘴淹没磨料射流场的数值模拟［J］.大庆石油学院学报，2011，35（1）：51-54.

［8］王文涛，胡胜勇.水力喷射钻孔技术在静北潜山油藏的试验研究［J］ .石油钻采工艺，2011，33（4）：19-22.

［9］黄卫星，陈文梅.工程流体力学［M］.北京：化学工业出版社，2001.

［10］孙晓超.水力深穿透水平钻孔技术的研究［D］.大连：大连理工大学，2005：17-18.

［11］杨卫化.水力深穿透射孔技术研究［D］.大连：大连理工大学，2009：18-20.

CFD-based parameter optimization for self-propelled nozzle

WANG Changbin, WANG Min, XU Yang, WEI Wei
（Northeast Petroleum University, Daqing 163318, China）

In order to effectively penetrate borehole pollution belt and expand the drainage area, certain work was done to increase the oil recovery and ultimately realize the purpose of production and injection increasing. By building a three-dimensional model of the nozzle, with the help of simulation software Fluent, flow field characteristics of self-propelled nozzle was studied under the conditions of different nozzle diameter and different angle between fore and post nozzles. The trend of the recoil power, rock breaking power and propulsion power were calculated by combining flow field velocity distribution law with the relevant formula. The results show that with the increasing of post nozzle diameter and fore nozzle angle, the recoil power and propulsion power increase, and rock breaking power decreases; on the other hand, with the rising of fore nozzle diameter and post nozzle angle, the recoil power and rock breaking power decrease, and propulsion power increases. The matching program of nozzle obtained by above numerical simulation provides a reliable basis for the actual production.

hydraulic jet drilling; high-pressure water jet; self-propelled rock breaking; numerical simulation

TE248

A

2012-06-16）

〔编辑 景 暖〕

1000 - 7393（ 2013 ） 01 - 0108 - 04

王常斌，1964年生。2004年毕业于浙江大学力学系，主要从事石油工程和计算流体力学方面的研究工作，博士。E-mail：wcb0917@sina.com。联系人：王敏，电话：13614644635。E-mail：wangminmin2006@sina.com。

王常斌，王敏，徐洋，等.基于CFD的自进式喷嘴参数优化［J］. 石油钻采工艺，2013，35（1）：108-111.