基于遥感图像信息特征的单调递增SSDA算法
2013-07-05司寒羽
王 杉,陈 翔,司寒羽
(华东交通大学信息工程学院,江西南昌330013)
遥感是通过不与物体、区域或现象接触获取调查数据,并对数据进行分析从而得到物体、区域或现象的有关信息的一门科学和技术[1]。它是人类在模拟人的视觉系统基础上逐步发展起来的一种高科技观测技术,通过检测和度量地物目标电磁辐射能量所得到的客观记录,把人眼看得到的和看不到的景物都转化为人眼所能看到的图像,重现地物目标电磁辐射特性的空间分布状况[2]。由于遥感能够提供大尺度(宏观)、动态的观测且不受地理位置、天气和人为条件限制,以不同的时空尺度不断地提供多种地表信息[3],所以遥感图像已被广泛应用于环境监测、资源探测、生态研究、测绘制图、军事指挥等众多领域。例如利用遥感图像观测云的移动(台风)、云量、地热、水色等[4]全球性同步观测数据已服务于人们的日常生活。
而遥感图像配准是指将取自同一目标区域的两幅或多幅图像在空间位置上最佳匹配起来,这些图像可以是由同一传感器在不同时间获取的,也可以是来自不同的传感器[5]。遥感图像具有观测目标细节能力强、观测范围广的特点,因此遥感图像的实时性配准一直都是遥感图像研究中最主要的难题之一[6]。利用来源于图像的信息特征进行图像配准能够获得可信度高、信息完善的目标真实状态和细节,从而大大提高了在复杂背景和干扰存在的情况下目标识别的正确率[7]。
近二十年来,图像配准技术的研究取得了重大进展,涌现出了多种方法,主要分为基于像素相似性的方法和基于特征的方法[8]。而目前针对高分辨率图像较常用的配准方法是采用基于图像灰度信息的定位算法。通常直接利用整幅图像的灰度信息建立两幅图像之间的相似性度量,然后采用某种搜索策略寻找使相似性度量值最大或最小的变换模型的参数值[9]。这种匹配方法采取的是一种遍历性搜索策略,需要在搜索区域内所有像素点上进行一对一的区域相关配准计算,数据量和计算量很大,配准速度较慢,对算法的实时性有很大影响[10-11]。为了减少匹配相关运算量,在文献[12]中,Barnea提出了一种序列相似性检测算法(SSDA)。该算法能很快丢弃不匹配的点,减少花在不匹配点上的计算量,从而提高匹配速度。但这类算法依然存在实时性差等缺陷。
基于图像信息特征的匹配方法可以克服上述算法的不足,由于图像的特征点比像素点要少很多,从而大大减少了匹配过程的计算量。同时特征点的匹配度量值对位置的变化比较敏感,角点作为图像最为重要的特征点,对图像图形的理解和分析有很重要的作用。通过对遥感图像角点的提取,可以有效提高匹配的精度和效率[13-14]。基于图像特征的匹配通常是利用图像中位置相对不变的特征来进行匹配的,可以克服灰度相关匹配的一些缺点,但是图像特征的提取和定位通常是比较困难,如果原图像和参考图像是比较复杂的图像时匹配是很难获得好的效果。
因此,在传统SIFT的基础上,利用圆形结构的旋转不变性,结合主成分分析法(principal component analysis,PCA),提出一种PCA-圆形SIFT特征点描述符提取图像特征角点。通过分析单调递增阈值序列SSDA算法的特点,结合图像特征点匹配,提出一种基于图像信息特征的单调递增阈值序列SSDA配准算法,最后通过实验仿真该算法的可行性。
1 基于PCA-圆形结构SIFT特征点的提取
SIFT特征检测算法是Lowe提出的一种基于尺度空间的,对图像缩放、旋转甚至仿射变换保持不变性的图像局部特征描述算子[15]。SIFT特征描述算子的生成一般包括以下几个步骤:
1)构建尺度空间,检测极值点,获得尺度不变性;
2)特征点过滤并进行精确定位;
3)为特征点分配方向值;
4)生成特征描述子;
5)特征向量的匹配。
本文在传统SIFT的方法基础上,鉴于圆具有很好的旋转不变性,引用了一种用圆形结构来构造SIFT特征点描述符,并结合PCA方法,建立了一种PCA-圆形结构SIFT算法。该算法通过降维的方式,极大地减少了计算过程,提高了运算速率,并且有效提取了特征点。
1.1 传统SIFT特征向量的生成
对每一个筛选出的特征点,要以此特征点作为中心点,在这个点的周围选取一个大小为16×16的区域,再将这个所选取区域平均分成4个大小均为4×4的小区域,并且计算每个小区域的梯度直方图,直方图包含有8方向,这样就获得了一个4×4×8=128维的向量,也就生成了SIFT特征描述符向量,直方图的峰值就是所选特征点的主方向。
1.2 圆形结构SIFT特征向量的生成
图1(a)的中心点表示SIFT特征描述符提取的特征点位置点P(t1,t2),设半径为r,确定圆形区域为(x-t1)2+(x-t2)2=r2式中,r是控制圆形区域的半径,最大取值为8。构造4个半径不同的同心圆环,这样就把圆形窗口分成4个圆环形区域。原算法在4×4的方形窗口内计算8个方向的梯度方向直方图,改进算法则是在以特征点为中心的圆形区域内构造4个圆环,在每个圆环内分别计算0°~360°均匀分布的12个方向上的梯度直方图。

图1 改进的SIFT特征点描述符Fig.1 The feature point descriptor of improved SIFT
图1(b)所示为内圆生成的12个方向的特征向量。具体统计过程为:如果某个像素点梯度方向落在图1b)某个箭头方向(即梯度方向)附近,则其相应的梯度高斯加权幅值就累加在这个方向上,这样就可以用梯度直方图统计出内圆梯度的累加值,再将这些梯度累加值从小到大排列。内圆的12个梯度累加值排列后作为1~12维的特征向量,次外圆梯度累加值排列后作为13~24维的特征向量,依次类推。4个同心圆环有4×12共48维特征向量作为特征点的描述符[16-17]。
1.3 PCA-圆形结构SIFT特征向量的生成
PCA-SIFT描述符与标准SIFT描述符具有相同的亚像素位置(sub-pixel)、尺度(scale)和主方向(domi⁃nant orientations),但在特征描述符生成时有所不同,PCA-SIFT[18-19]通过PCA方法将传统SIFT的128维特征向量进行降维,以达到更精确的表示方式。
由1.2节可知,采用圆形结构SIFT可以将传统128维SIFT特征向量维数降低至48维。本节将结合PCA方法,对48维的圆形结构SIFT特征点描述符继续降维,进一步减少了计算量,提高了精确度。利用PCA方法对基于圆形结构48维SIFT特征描述符进行降维的具体方法如下:
1)输入两幅待匹配图像中所有关键点(设为n个)的48维SIFT特征描述符,将输入的这n个特征描述符作为样本,写出样本矩阵为,其中xi表示第i个特征点的48维特征向量。
2)计算n个样本的平均特征向量
3)计算所有样本点的特征向量与平均特征向量的差,得到差值向量di=xi-,i=1,2,…,n。
5)求协方差矩阵的48个特征值λi和48个特征向量ei。
6)将求出的48个特征值按从小到大的顺序进行排列λ1≥λ2≥…≥λ48和对应的特征向量[e1,e2,…,e48]。
7)选取对应t个最大特征值的特征向量作为主成分的方向,在实验中选取t=12。
8)构造一个48×12的矩阵A,它的列由t个特征向量组成。
9)把原始的48维SIFT描述符依据式(6)投影到所计算出的n维子空间M中,就可以得到PCA-SIFT的描述符y1,y2,…,yn,即yi=xiA。
因为实验中选取t=12,所以矩阵A的大小为48×12,xi的大小为1×48,所以xiA就得到了一个大小为1×12的矩阵,即每一个yi就是一个12维的特征描述符,也就是把原来的48维传统SIFT特征描述符降成了12维的PCA-SIFT特征描述符。
本文通过PCA-圆形结构SIFT的建立,将传统SIFT 128的特征描述符,通过先建立圆形结构,后结合PCA方法两个步骤降成了12维的特征描述符。为下一步特征向量的匹配,由原先采用欧式距离对具有128维的特征点描述子的相似性进行度量,变成了现在采用欧式距离对具有12维的特征点描述子的相似性进行度量,减少了数以十倍的计算量,极大的简化了计算过程,节约了匹配算法的运行时间。
2 模板的图像匹配
2.1 传统SSDA算法
序贯相似性检测算法(sequential similarity detection algorithms,SSDA)将大小为M×M的模板T在大小为N×N的搜索图S上平移,模板覆盖下的那块搜索图设为子图Sij,i,j为这块子图的左上角像点在S中的坐标,则i和j的取值范围为1≤i,j≤N-M+1,如图2所示。SSDA的算法过程如下[20-22]:
1)定义绝对误差:

其中
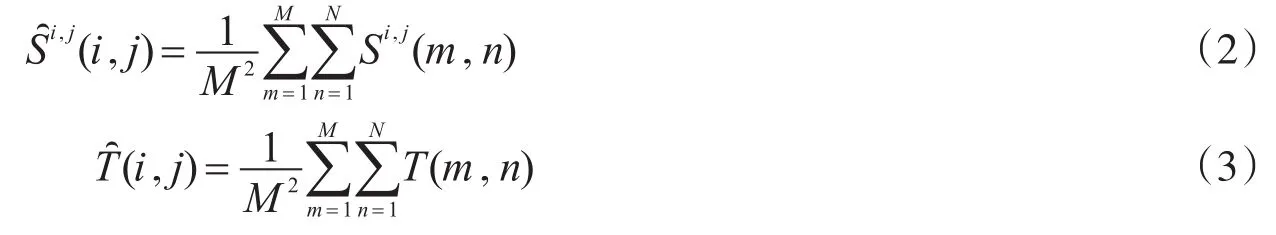

图2 被搜索图S和模板TFig.2 The search figure S and the template T
2)取一固定阈值Tk。
3)在子图Si,j(m,n)中随机选取对象点。计算它同T中对应点的误差值,然后把这个差值和其他点对的差值累加起来,当累加r次误差超过Tk,则停止累加,并记下次数r,定义SSDA的检测曲面为

4)把I(i,j)值大的(i,j)点作为匹配点,因为这点上需要很多次累加才使总误差超过Tk,如图3所示,图中给出了A,B,C这3个参考点上得到的误差累计增长曲线。A,B反映了模板T不在匹配点上,这时总误差增长很快,超出阈值,而曲线C中总误差增长很慢,很可能是一套准确的候选点[23]。
2.2 单调递增阈值序列SSDA算法
基本SSDA算法所选取的阈值T是固定的,对于不同区域上子图的阈值选取并不一定是最佳的,容易受到噪声影响,而且计算量较大。如果采用一种单调增长的阈值序列[17],使非匹配点用更少的计算就达到阈值而被丢弃,真匹配点需更多次误差累计才达到阈值,则能够使阈值T逐渐逼近最佳阈值,从而增加了SSDA算法的准确性,使得匹配速度大大提高,如图4所示。

图3 Tk为常数时的累计误差增长曲线Fig.3 Accumulative error growth curves whenTkis constant
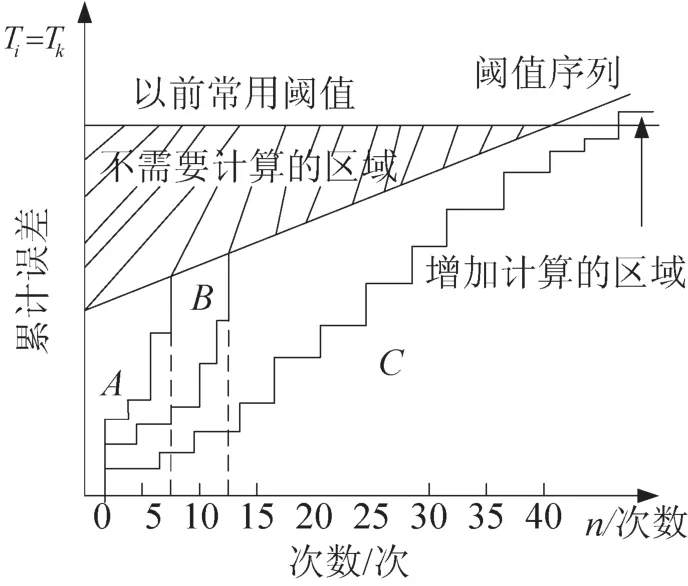
图4 Tk用单调增加阈值序列的情形Fig.4 Accumulative error growth curves whenTk is monotonically increasing
由于除匹配点以外,绝大数的情况下都是对非匹配点计算的,显然,越早丢弃非匹配点将节省时间。根据上文传统的SSDA算法介绍,增长曲线A,B反映了模板T不在匹配点上,可以发现,A,B在很早的时候就已经达到阈值而被抛弃,和图2相比,图4单调增加阈值算法A,B点经历了更少次的运算,图4中斜线区域的面积为此算法所节省的计算量。曲线C中总误差增长缓慢,很可能是一套准确的候选点。基于以上思想,本文提出的改进算法如下:
在匹配过程中,先要获得初始匹配点(x,y),并且需要制定一个初始阈值T。可以设置一个较小的数值作为初始门限,初始匹配点可以设置为(0,0),然后使模板图像与所取到的特征点做相关运算。在待匹配图像中每个特征点处同样利用到公式(1)计算模板图与搜索子图的相关测度ε(i,j)。如果在计算像素点相关测度ε(i,j)的过程中,ε(i,j)累积超过阈值T,就停止该像素点的相关性计算,并且把此时计算所得的ε(i,j)作为新的门限阈值,并以此阈值去计算下一个像素点的相关测度值ε;如果计算完该搜索子图,而ε仍然小于阈值T,则更新匹配点为此次运算的运算位置。用公式表示为

3 本文遥感图像匹配流程图
先将原图像和模板图像通过基于PCA-圆形结构SIFT特征点描述符提取图像角点,将此角点作为单调递增阈值序列SSDA算法的基本像素点,通过模板匹配,最后完成图像匹配。
基本的SSDA模板匹配在选取随机点时会找到误差较大的点,从而及早地结束匹配计算过程。相比之下,利用图像自身信息特征可以及时发现并排除孤立的像素点,具有较强的抗干扰能力;而且只利用图像的特征点进行匹配,能够大大减少匹配过程的计算量。先利用基于特征的方法获得一个粗略的匹配,然后利用基于单调递增SSDA方法对结果进行进一步的优化,达到精匹配。

图5 遥感图像匹配流程图Fig.5 The flow chart of remote image registration
4 实验结果及分析
为了验证本文所提出算法的高效性,对固定阈值SSDA算法、单调递增阈值序列的SSDA算法以及基于图像信息特征的单调增长阈值序列SSDA配准算法在处理时间上做了比较。处理结果,如图(6)所示。

图6 实验数据源及结果Fig.6 Experimental data sources and results
图6中,选取两幅图作为图像匹配实验图,第一幅为探测地球外小行星遥感图像,第二幅为中国气象局发布的风云二号气象卫星云图。其中(a),(b),(c)为第一幅图的图像匹配序列,(a)为待匹配图像,尺寸为170×130,(b)为模板图像,尺寸为30×30,(c)为匹配结果。(d),(e),(f)为第二幅图的图像匹配序列,(d)为待匹配图像,尺寸为1 720×1 290,(e)为模板图像,尺寸为179×166,(f)为匹配结果。
通过统计各种算法在此两组实验对象的匹配时间,由表1可知,单调递增阈值序列SSDA算法与固定阈值SSDA算法相比能较大的提高匹配速度,但由于随机点选取方式的影响,使得模板与子图的大多数点都需进行匹配,算法速度仍不理想,而基于遥感图像信息特征的单调递增阈值序列SSDA算法则能较好的解决这一问题。这种算法利用图像信息特征选取匹配点的方式可以提高匹配精度。

表1 各种算法处理时间比较Tab.1 Processing time comparison between different algorithm
本文利用优化的PCA-圆形结构SIFT算法结构提取图像特征角点,降低了特征描述符的维数,减少相似性度量计算,由此方法建立特征点集,然后采用单调递增阈值序列SSDA算法进行精确匹配。该气象图像配准系统不但减少了计算量,缩短了匹配时间,而且也表现出了更好的抗噪声能力。通过分析可知,在图像尺寸较大的情况下,本文算法优势更加明显。
5 结束语
遥感图像的实时性配准一直以来都是制约遥感图像处理高效性的一个瓶颈。由于遥感图像观测范围广,包含信息量大,一般的配准算法很难满足在保证其配准精度的前提下实时性方面的需求。本文以经典SSDA为基础,针对现有算法存在的问题,提出一种基于图像信息特征单调递增阈值序列的匹配算法,大大减少了过程的计算量,提高了匹配的精度。另外,在实际应用中,可以结合粗-细分层搜索策略等进一步提高匹配性能。
[1]LILLESAND T M,KIEFER R W.遥感与图像解译[M].彭望绿,余先川,周涛,等,译.4版.北京:电子工业出版社,2003:1-34.
[2]戴昌达,姜小光,唐伶俐.遥感图像应用处理与分析[M].北京:清华大学出版社,2004:3-75.
[3]赵英时.遥感应用分析原理与方法[M].北京:科学出版社,2003:309-414.
[4]MAITRE H,PINCIROLI M.Fractal characterization of a hydrological basin using SAR satellite images[J].IEEE Transactions on Geoscience and Remote Sensing,1999,37(1):175-181.
[5]饶俊飞.基于灰度的图像匹配方法研究[D].武汉:武汉理工大学,2005.
[6]雷琳,李智勇,粟毅.利用多特征融合匹配实现遥感图像多目标关联[J].信号处理,2009(3):454-459.
[7]章毓晋.图像分割[M].北京:科学出版社,2001:39-45.
[8]梁青,蒋先刚,沈涛.基于颜色互信息的病变细胞图像配准算法研究[J].华东交通大学学报,2011,28(4):14-18.
[9]TTTI L,KOCH C,NIEBUR E.A model of saliency-based visual attention for rapid scene analysis[J].IEEE Transactions on PatternAnalysis and Machine Intelligence,1998,20(11):1254-1258.
[10]OLSON C F,HUTTENLOCHER D P.Automatic target recognition by matching oriented edge pixels[J].IEEE Transaction son Image Processing,1997,6(1):103-113.
[11]TTTI L,KOCH C.Computational modeling of visual attention[J].Nature Reviews Neuroscience,2001,2(3):194-203.
[12]BARNEA D I,SIVERMAN H F.A class of algorithms for digital image registration[J].IEEE Trans Computers,1972,21(2):179-186.
[13]HATABU A,MIYAZAKI T,KURODA I.Optimization of decision-timing for early termination of SSDA-bassed block matching[C]//International Conference on Multimedia and Expo Piscataway,NJ:IEEE,2003:821-824.
[14]HONG ZHENHUA,ZHU PEIYING.An improved SSDA applied in target tracking[C]//Pattern Recognition 9th IEEEE International Conference,Hardware Software:Computing&Processing,1988:767-769.
[15]王敬东,徐亦斌,沈春荣.一种新的任意角度旋转的景象匹配方法[J].南京航空航天大学学报,2005,37(1):6-10.
[16]姚文伟,张智斌,李国,等.图像匹配算法 SIFT的改进[J],郑州轻工业学院学报,2011,26(6):67-70.
[17]吴若鸿,基于特征匹配的双目立体视觉技术研究[D].武汉:武汉科技大学,2010.
[18]马莉,韩燮.主成分分析法(PCA)在 SIFT 匹配算法中的应用[J].电视技术,2012,36(1):129-132.
[19]ATSUSHI H,TAKASHI M,ICHIRO K.Optimization of decision-timing for early termination of SSDA-bassed block matching[C]//Acoustics,Speech,and Signal Processing,Proceedings(ICASSP 03),2003 IEEE International Conference,2003:821-824.
[20]TAUBMAN D.High performance scalable image compression with EBCOT[J].IEEE Trans on Image Processing,2000,9(7):1158-1170.
[21]刘海波.Visual C++数字图像处理技术详解[M].北京:机械工业出版社,2010:293-296.
[22]沈庭之,方子文,数字图像处理及模式识别[M].北京:北京理工大学出版社,1998:151-152.
[23]LOWE D.Distinctive image features from scale-invariant key-points[J].Int J of Comp Vision,2004,60(2):91-110.
