互联电网AGC的分数阶PID控制

杨平，董国威

（上海电力学院电力与自动化工程学院，上海 200090）

互联电网AGC的分数阶PID控制

杨平，董国威

（上海电力学院电力与自动化工程学院，上海 200090）

控制性能标准（CPS）下的互联电网自动发电控制（AGC）的控制策略已经取得一些进展。分数阶PID的较强的鲁棒性和非线性适应能力的特征已引起研究人员关注。文中研究了将分数阶PID应用于互联电网AGC控制的问题，并且总结了参数λ、μ的整定规律。仿真结果表明，互联电网AGC的分数阶PID控制系统具有鲁棒性强和非线性适应能力好的优点，并且在CPS指标考核上也比传统PID控制器强。

分数阶；比例积分微分（PID）；互联电网；自动发电控制（AGC）；控制性能标准（CPS）

近年来，社会对电力能源的需求量和质量的要求促进了对互联电网自动发电控制（AGC）的持续关注和深入研究，并已经取得一些进展。文献[1]提出了采用强化学习控制器代替传统的PI（proportional-integral）调节器；文献[2]使用粒子群算法对模糊控制器进行优化。文献[3]提出了一种自整定控制方案用于带有超导磁能存储SMES（superconducting magnetic energy storage）控制的两区域的AGC控制。文献[4～6]提出的CPS标准下的AGC控制策略则比较基础和实用，在我国电网中已多有实际应用。这些实用的控制策略并没有直接利用CPS标准的考核指标数值信息，而是通过使CPS标准的考核指标变好的定性分析中提取控制策略，这些定性化的智能控制策略已被证明是简单而有效的。文献[7，8]提出的CPS标准下的AGC控制策略引入了学习算法，根据CPS统计指标调整AGC控制的松紧程度。文献[9]不但从CPS指标的角度进行控制分析，还从DCS指标的角度来进行分析。文献[10]采用标准粒子群优化算法PSO（particle swarm optimization）对CPS控制策略中AGC机组调节功率的分配进行机组种群优化。总之，互联电网自动发电控制（AGC）的研究可大致分为两个方向：依据功率偏差和频率偏差的控制规律和依据CPS统计指标优化调整规律。前者指PID（proportional-intengral-derivative）、模糊控制、自校正控制等规律，后者指强化学习、粒子群优化、自学习、智能松紧控制等策略。在依据功率偏差和频率偏差的控制规律方面，用的最多的还是PID及其改进型。这不但是因为PID已被工程界所熟知，而且其容易实现又有鲁棒性好和适应面宽的优势不容置疑。进而PID改进型的研究热经久不衰。所以，分数阶PID控制用于互联电网AGC的研究课题，既有理论研究价值又有工程应用意义。

分数阶PID控制器最早由Podlubny教授[11]提出的。由于引入了任意实数的积分阶次λ和微分阶次μ，所以相对于传统的整数阶PID多了两个可调参数，控制器特性范围变大了，可以实现阶次的无级调整。有文献指出，分数阶PID控制器的优势在于鲁棒性很强，尤其对非线性过程有更强的适应性[12]。因此，将分数阶PID控制器应用于非线性和需要强鲁棒性的工业过程是有优势的。文献[13]给出了分数阶PID控制器应用于锅炉-汽轮机系统控制的研究结果，得出了具有良好的适应性及鲁棒性的结论。文献[14]给出了分数阶PID控制器应用于负荷频率控制系统LFC（load-frequency control）的研究结果，研究重点在负荷变动下的控制性能上，但并未考察有非线性和过程参数变化的情况。在互联电网AGC控制系统中，非线性特性是肯定存在的。除了发电主设备中内含的非线性外，控制设备内也有非线性环节，如执行器、限幅器等等。因此，以下所述的分数阶PID控制器应用于互联电网AGC控制的考察研究侧重点在于鲁棒性和非线性性能两个方面。

1 分数阶微积分与分数阶PID控制器

1.1 分数阶微积分

分数阶微积分的基本操作算子为aDtα，其中a和t是操作算子的上下限，α为微积分阶次。常见的分数阶微积分定义是Grunwald-Letnikov定义，有

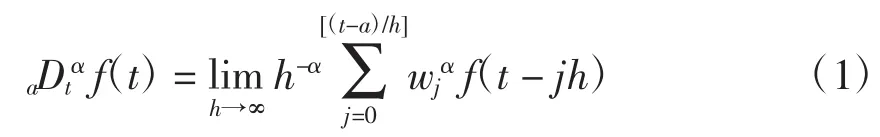
1.2 分数阶PID控制器

分数阶PIλDμ控制器的微分方程为

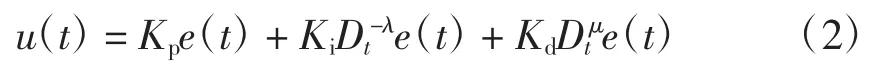
式中：λ为积分阶次；μ为微分阶次。式（2）经拉氏变换并整理后可得分数阶PID的传递函数为

可以认为式（1）中wjα是（1+z）α在原点的泰勒展开式的系数，再对式（2）进行离散化处理，可得控制器的离散计算式为

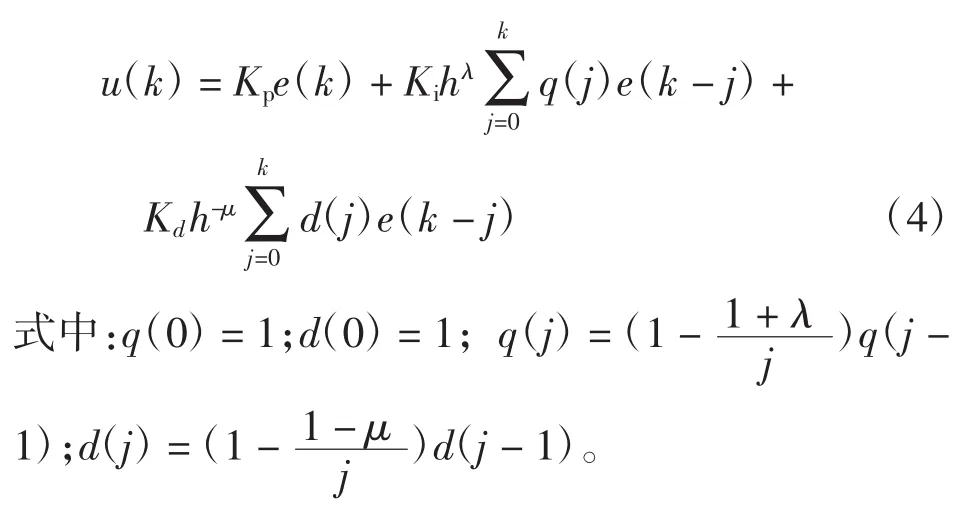
由于λ和μ可以取任意实数，因此，整数阶PID只是分数阶的特例。在λ-μ平面上，整数阶PID只对应于若干个点：P（0，0）、PD（0，1）、PI（1，0）、PID（1，1）。而分数阶PID可以取整个λ-μ平面中的任意点。故分数阶PID控制器所能实现的特性远比整数阶PID要宽。一个整数阶PID只可实现线性二阶环节的特性。而分数阶PID可以实现任意阶（如1.5阶或0.7阶）的线性环节的特性。换句话说，分数阶PID可提供了更多的控制自由度，从而具有了进一步提高PID控制器效能的潜力。

2 互联电网AGC系统仿真模型

2.1 两区域互联电网模型

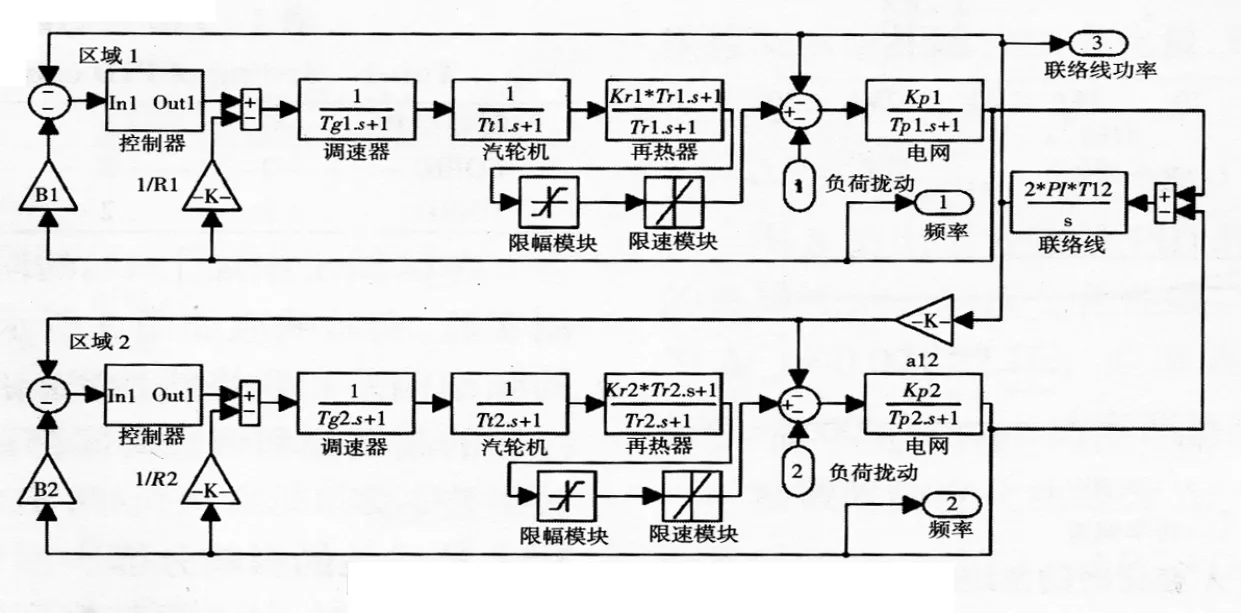
图1 两区域控制系统仿真模型Fig.1Simulink model of a two-area power system

为研究分数阶PID在互联电网AGC的应用问题，采用了如图1所示的一种两区域互联电网AGC仿真模型。假设区域1和区域2均为2 000 MW，故设定参数a12=-Pr1/Pr2=-1；区域中汽轮机和发电机速度限制为3%/min。

根据文献[15]，仿真系统中各参数为：第i区域调速器时间常数Tgi=0.08 s、汽轮机时间常数Tti= 0.3 s、再热器时间常数Tri=10 s、再热器的比例系数Kri=0.5、电网的时间常数Tpi=20 s、电网的比例系数Kpi=120 Hz/（p.u.·MW），联络线时间常数T12=0.544 s。

2.2 控制器模型

在每个控制区域中，分别使用整数阶PID（IOPID）和分数阶PID（FOPID）作为AGC控制器，控制器结构如图2所示。FOPID控制器模块是根据式（4）用S函数编程实现的。

图2 控制器结构Fig.2Structural model of controller

3 电网AGC的分数阶PID控制仿真实验研究

3.1 参数λ、μ的整定

在负荷扰动1%的情况下，设定控制器参数，Kp=2；Ki=1.2；Kd=1.3；μ=1时，λ分别取0.8、1.0、1.2；再设定λ=1时，μ分别取0.8、1.0、1.2。

电网AGC的分数阶PID控制经过多次仿真试验，结果如图3和图4所示。

图3 参数λ变化时的系统响应Fig.3Output of the system with the change of λ

从图3可知，λ适当减小，可以降低控制区域频率控制过程中的超调量和调整时间，也可以降低联络线功率控制过程的超调量和调整时间，但是会降低主控区域（区域1）和随动区域（区域2）的CPS1指标；反之增大λ则可以大幅改善两区域的CPS指标，但是会稍微损失控制过程的动态性能。

图4 参数μ变化时的系统响应Fig.4Output of the system with the change of μ

从图4可知，μ适当减小则可以降低区域频率控制和联络线功率控制过程中的超调量，但是会略微增加调整时间；μ适当增加则可以降低区域频率控制和联络线功率控制过程的调整时间，但是超调量会加大。参数μ在等于1的基础上适当的增加或者减少时，对主控区域的CPS1指标都有所改善，但是会降低随动区域的CPS1指标。

3.2 负荷扰动性能分析

设定两区域电网的区域频率调差参数为R1= R2=4%，频率偏差系数为B1=B2=0.425，通过反复实验得到PID控制器的最佳参数，其具体参数如表1所示。

表1 PID控制器参数设定Tab.1Setting of PID controller parameters

在区域1中加上1%的阶跃负荷扰动进行控制实验，实验响应如图5所示。可以看出，区域1的频率偏差和联络线功率响应表明，分数阶PID控制的超调量和调整时间都跟整数阶PID控制的效果差不多。

3.3 非线性的影响分析

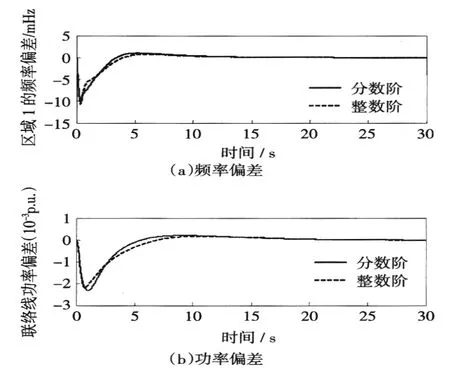
图51 %负荷扰动系统输出Fig.5Output of the system with 1%load disturbance

从图1的AGC系统模型可以看到，在再热器的出口处有一个限幅限速模块。这个非线性环节的存在意味着所采用的控制器的不得不面对非线性过程的控制挑战。图6给出了限幅限速模块在1%的负荷扰动和3%的负荷扰动下的输入输出曲线，其中实线代表仿真系统中非线性环节的输入信号，虚线代表仿真系统中非线性环节的输出信号，对比输入和输出信号即可观察出仿真系统中非线性环节的工作情况，其纵坐标仅代表信号量的大小。显然，在1%的负荷扰动时，信号没有超过限幅限速器的界限，因此非线性环节不工作，可以认为此时的AGC系统是一个线性系统；而在3%的负荷扰动时，非线性环节起作用了，此时的AGC系统是一个非线性系统。

图6 限幅限速模块的变量Fig.6Variables of amplitude and rate limiter

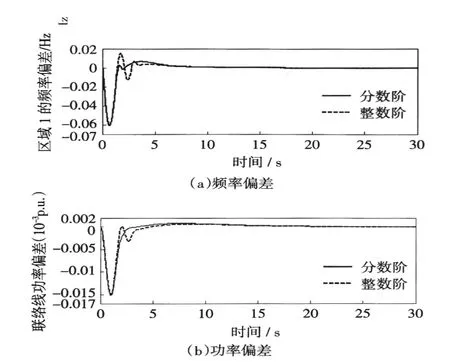
图73 %负荷扰动系统输出Fig.7Output of the system with 3%load disturbance

图7所示响应为在3%负荷扰动的控制响应，也就是非线性系统控制响应。对比图7与图5显见，在动态性能上，由于非线性的作用，使得整数阶PID的响应曲线不是很平滑，而且振荡较为剧烈，分数阶PID的响应曲线相对较好，振荡明显更少一些。因此分数阶PID控制器比整数阶PID控制器的控制改善更多一些。可以说，分数阶PID控制器具有更佳的非线性控制性能。

3.4 鲁棒性能分析

一般可通过仿真实验方法来确定某控制系统的鲁棒性优劣。其仿真实验的做法是先进行被控过程参数变化前后的参比控制系统仿真实验，再进行被控过程参数变化前后的某控制系统仿真实验，然后对比在同样的被控过程参数变化前后的控制响应变化幅度，其变化幅度较小者的鲁棒性更优。

现研究互联电网AGC分数阶PID控制系统的鲁棒性，以整数阶PID控制系统为参比系统，更改电网负荷模型的时间常数为Tpi=40 s（原先Tpi= 20 s），控制参数、系统参数均不变，负荷扰动1%。分别进行被控过程参数变化前后的控制响应实验。为了便于比较，将被控过程参数变化前后的两次控制响应相减得出变化量，即

图8给出了分数阶PID和整数阶PID控制器的鲁棒性试验响应变化曲线。分数阶的变化曲线为Δfm=0.001 22 Hz；频率调整时间Δth=13.1 s；ΔPm=0.000 38 p.u.；功率调整时间ΔtP=8.3 s。

整数阶的变化曲线为Δfm=0.001 51 Hz；频率调整时间Δtf=17.3 s；ΔPm=0.000 47 p.u.；功率调整时间ΔtP=11.7 s。

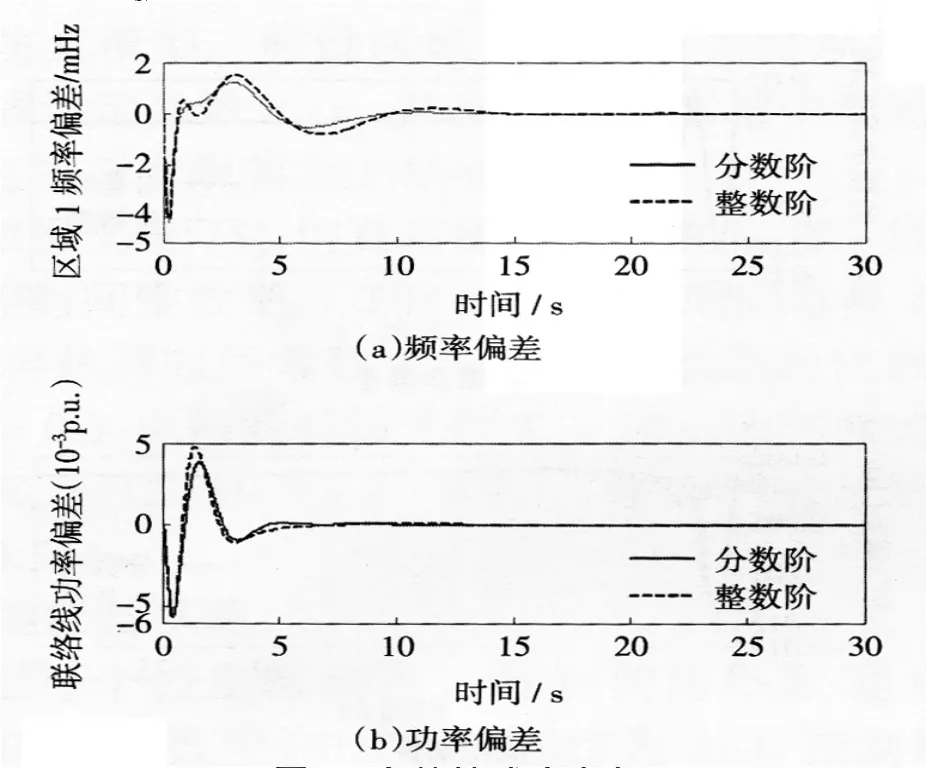
图8 鲁棒性试验响应Fig.8Output of the system for robustness

显然，互联电网AGC分数阶PID控制的响应变化幅度更小。也就是说，分数阶PID的鲁棒性更强。

3.5 CPS指标分析

CPS标准自1998年北美电网实行以来，各国也纷纷采用CPS标准来对电网进行考核。自2001年华东电网率先在我国采用CPS标准进行考核以来，国内其他电网也相继采用CPS标准进行考核。CPS标准是基于统计学原理的指标，采用CPS标准进行考核，可以提高电网电能质量、安全性、可靠性，充分发挥大电网联网的优势，各区域之间相互支援[16]。在考察分数阶PID在AGC的应用效果时，测取其CPS性能指标是很有专业意义的。

CPS1指标为在一个给定的时间间隔内，一个控制区域的（ACE除以它10倍的偏移量）每分钟的平均值与相应的1 min联络线频率偏差的平均值的积的平均值，应不大于ε12常数。

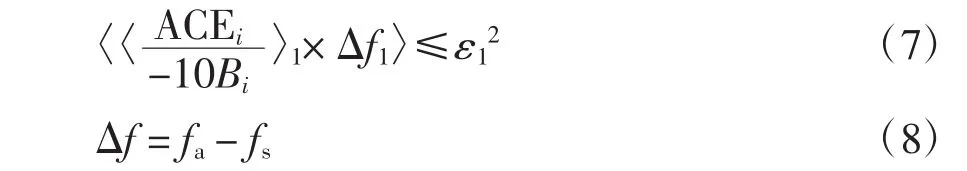
对于某一段时间（如10 min、1 h、1月、1 a）的CPS1指标KCPS1的统计公式为

式中：KCF为特征变量；n为分钟数。

在区域1加入一个幅度为3%、周期为3 s的方波信号负荷扰动，测取两区域的CPS1指标如图9所示。可以看出，分数阶PID控制器的CPS1指标

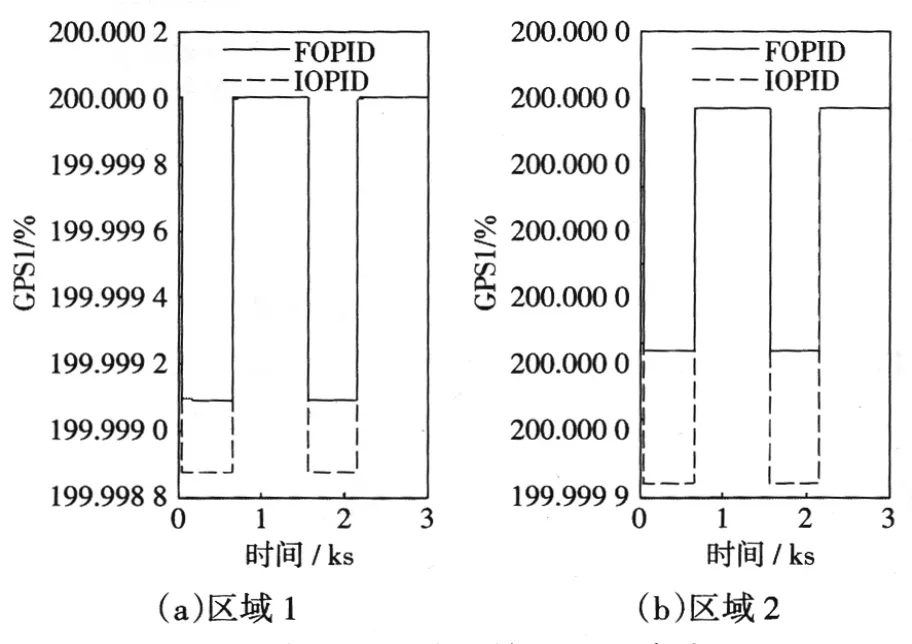
图9 区域1和区域2的CPS1统计结果Fig.9CPS1 statistic results of area1 and area2

4 结论

（1）在非线性和鲁棒性两方面，分数阶PID控制器均比整数阶PID控制效果更好。

（2）在CPS1指标考核中，分数阶PID控制器明显优于整数阶PID控制器。

（3）参数λ减少可以提高控制过程的动态性能，但是会降低两区域的CPS指标，增加λ则效果相反。

（4）参数μ减少可以减小超调量、增大调整时间，增加μ则反之，但是在一定范围内无论μ增加还是减少都会增大主控区域的CPS指标，降低随动区域的CPS指标。

[1]李红梅，严正（Li Hongmei，Yan Zheng）.具有先验知识的Q学习算法在AGC中的应用（Application of Q-learning approach with prior knowledge to non-linear AGC system）[J].电力系统自动化（Automation of Electric Power Systems），2008，32（23）：36-40，99.

[2]Sinha S K，Prasad R，Patel R N.PSO tuned combined optimal fuzzy controller for AGC of two area interconnected power system[C]//World Congress on Nature&Biologically Inspired Computing.Coimbatore，India：2009．

[3]Sheikh M R I，Muyeen S M，Takahashi R，et al.Application of self-tuning FPIC to AGC for load frequency controlin multi-area power system[C]//IEEE Bucharest PowerTech.Bucharest，Romania：2009．

[4]高宗和，滕贤亮，涂力群（Gao Zonghe，Teng Xianliang，Tu Liqun）.互联电网AGC分层控制与CPS控制策略（Hierarchical AGC mode and CPS control strategy for interconnected power systems）[J].电力系统自动化（Automation of Electric Power Systems），2004，28（1）：78-81．

[5]高宗和，滕贤亮，张小白（Gao Zonghe，Teng Xianliang，Zhang Xiaobai）.互联电网CPS标准下的自动发电控制策略（Automatic generation control strategy under control performance standard for interconnected power grids）[J].电力系统自动化（Automation of Electric Power Systems），2005，20（19）：40-44．

[6]唐跃中，张王俊，张健，等（Tang Yuezhong，Zhang Wangjun，Zhang Jian，et al）.基于CPS的AGC控制策略研究（Research on control performance standard based control strategy for AGC）[J].电网技术（Power System Technology），2004，28（21）：75-79．

[7]余涛，陈亮，蔡广林（Yu Tao，Chen Liang，Cai Guanglin）.基于CPS统计信息自学习机理的AGC自适应控制（CPS statistic information self-learning methodology based adaptive automatic generation control）[J].中国电机工程学报（Proceedings of the CSEE），2008，28（10）：82-87．

[8]余涛，周斌（Yu Tao，Zhou Bin）.基于强化学习的互联电网CPS自校正控制（Reinforcement learning based CPS self-tuning control methodology for interconnected power systems）[J].电力系统保护与控制（Power System Protection and Control），2009，37（10）：33-38．

[9]李正，敬东，赵强，等（Li Zheng，Jing Dong，Zhao Qiang，et al）.CPS/DCS标准在大区互联电网AGC控制策略中的应用（Application of AGC control strategy based on CPS/DCS standards in interconnected power system）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2003，15（2）：27-32，48．

[10]刘斌，王克英，余涛，等（Liu Bin，Wang Keying，Yu Tao，et al）.PSO算法在互联电网CPS功率调节中的应用研究（Study on the application of particle swarm optimization algorithm to power regulation of CPS in interconnected power grids）[J].电力系统保护与控制（Power System Protection and Control），2009，37（6）：36-39，52．

[11]Podlubny I.Fractional Differential Equations[M].New York：Academic Press，1999．

[12]赵春娜，赵雨，张祥德，等（Zhao Chunna，Zhao Yu，Zhang Xiangde，et al）.分数阶控制器与整数阶控制器仿真研究（Simulation research on fractional order controllers with integer order controllers）[J].系统仿真学报（Journal of System Simulation），2009，21（3）：768-771，775．

[13]王东风，王晓燕，韩璞（Wang Dongfeng，Wang Xiaoyan，Han Pu）.锅炉-汽轮机系统的分数阶控制器设计（Design of fractional order controllers for a boiler-turbine system）[J].中国电机工程学报（Proceedings of the CSEE），2010，30（5）：113-119．

[14]Alomoush Muwaffaq Irsheid.Load frequency control and automatic generation control using fractional-order controllers[J].Electrical Engineering，2010，91（7）：357-368．

[15]Elgerd O I.Electric Energy Systems Theory An Introduction（Second edition）[M].New Delhi：Tata McGraw-Hill，1983．

[16]Standard BAL-001-0.1a，Real Power Balancing Control Performance[S]．

[17]张斌.自动发电控制及一次调频控制系统[M].北京：中国电力出版社，2005．

Fractional Order PID Control for AGC of Interconnected Power System

YANG Ping，DONG Guo-wei
（School of Electric Power and Automation Engineering，Shanghai University of Electric Power，Shanghai 200090，China）

The automatic generation control（AGC）of an interconnected power system，based on the NERC's control performance standard（CPS），has made some forward.It has raised concerns that fractional order PID（proportionalintegral-derivative）controller is robust and suitable for the nonlinear systems.This paper studies how to use fractional order PID controller in the AGC of an interconnected power system and sums the parameter setting rules about λ and μ. The results of simulation show that in an AGC system，the fractional order PID controller is also robust，suitable for the nonlinear systems and more suitable for CPS assessment than the classical PID controller.

fractional order；proportional-integral-derivative（PID）；interconnected power system；autornatic generation control（AGC）；control performance standard（CPS）

TM734

A

1003-8930（2013）03-0124-06

杨平（1954—），男，教授，研究方向为电力自动化和计算机测控技术。Email：yangping1201@126.com

2011-11-16；

2012-04-12

上海市科委2010创新行动计划项目（10250502000）

董国威（1987—），男，硕士研究生，研究方向为电力系统及其自动化。Email：dgxt888@126.com