考虑随机特性的微电网电源优化配置

卢洋，卢锦玲，，石少通，杨仁刚

（1.华北电力大学电气与电子工程学院，保定 071003；2.中国农业大学信息与电气工程学院，北京 100083）

考虑随机特性的微电网电源优化配置

卢洋1，卢锦玲1，2，石少通1，杨仁刚2

（1.华北电力大学电气与电子工程学院，保定 071003；2.中国农业大学信息与电气工程学院，北京 100083）

对孤岛运行微电网进行合理地电源配置是保证其可靠经济运行的关键问题之一。以电源类型、接入位置与容量为待求变量，综合经济成本最低为目标函数，微电网节点电压为主要约束条件，建立了数学模型，并采用粒子群算法求解。考虑到常见微电网电源如风能、太阳能的随机特性，根据不同类型电源出力概率模型，采用蒙特卡洛法模拟电源的出力，并结合确定性潮流算法，建立了随机潮流计算方法。使用该随机潮流计算方法得到不同电源配置方案孤岛微电网的节点电压越限率，以此评价配置方案的可靠性。算例表明，使用该方法对孤岛微电网的电源进行配置，可以在控制投资成本的同时，有效地将节点电压越限率控制在较低水平，满足了经济性和可靠性的要求。

微电网；孤岛运行；粒子群优化；电源优化配置；随机潮流

作为大电网的有效补充，微电网在提高能源利用率、加强供电可靠性、响应负荷水平的快速变化等方面发挥着重要作用[1，2]。微电网既可以与大电网联网运行，也可以独立孤岛运行。在一些地区如边防哨所、岛屿、高海拔山区等采用常规电网供电存在输电距离远、线损大、建设变电站费用昂贵等问题，而采用微电网供电可以有效解决这些问题[3，4]。此时微电网表现为一个孤岛独立运行的有源自治电力系统，对该孤岛微电网进行相关研究具有重要意义。

对孤岛运行的微电网进行电源优化配置以提高其经济性和可靠性是微电网规划的重要问题之一。经济性方面，需要考虑微电源的投资、安装费用，投入使用后的运行费用、环境成本等。可靠性方面，在配置微电源后，需要保证微电网安全可靠运行，满足各项可靠性指标。此外，常见微电源如风能、太阳能等输出功率受自然因素影响，具有随机性和间歇性的特点，也是配置微电网电源需要考虑的问题。

配置微电网电源需要确定电源的类型、数目、容量及位置等，近年来，国内外众多学者对其展开了研究，取得了许多有意义的成果。文献[5]提出一种改进的细菌觅食算法对常年孤岛运行的风/光/储混合微电网电源配置进行了优化；文献[6]在综合考虑电网安全性和稳定性的前提下，定量分析分布式电源的环境效益，得到了较为合理的分布式电源选址和容量方案；文献[7]将模拟退火算法与粒子群算法结合，对分布式电源选址定容问题进行求解，使得加入DG后网损最小；文献[8]提出基于负荷组合匹配算法的微电网电源规划方案，根据负荷用电与电源发电最佳匹配关系确定供电区域，以单位发电成本最低为目标确定容量电源容量。文献[5～8]在解决分布式电源配置问题时均考虑了电网的经济性、可靠性，但均未考虑风能、太阳能随机性和波动性的影响，存在着一定的局限性。

本文使用粒子群算法解决全年孤岛运行微电网电源的定类、选址、定容等问题，保证经济性的同时考虑孤岛微电网节点电压越限率等可靠性指标。考虑到常见微电网电源如风能、太阳能随机性和波动性的特点，根据不同类型分布式电源出力的概率分布模型，采用蒙特卡洛法模拟电源的随机特性，结合确定性潮流算法，建立了随机潮流计算方法。使用该随机潮流计算方法计算不同电源配置方案下的电压越限率指标。将该指标与综合经济成本结合考虑，最终得到孤岛微电网电源最优配置方案。

1 微电网电源概率模型

1.1 风机模型

风力发电机的出力与风速相关，为了更为准确地描述风速分布情况，采用三参数Weibull分布[9]作为风速的概率密度函数，其表达式为

式中：v为风速，m/s；k为Weibull分布的形状参数k〉0；c为Weibull分布的尺度参数，c〉0；v0为Weibull分布的位置参数，v0〈vmin，m/s。

风力发电机的输出功率Pwt与风速v之间的关系可用函数[10]表示为

式中，k值通常取3。参数a、b分别为

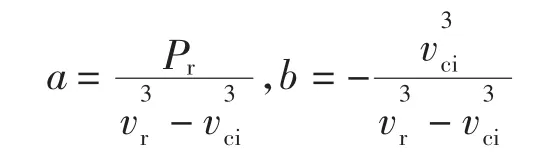
式中：Pr为风力发电机的额定功率；vci为切入风速；vr为额定风速；vco为切出风速。

输出功率曲线如图1所示。

图1 风力发电机输出功率与风速的关系Fig.1Relationship between output power and wind speed of a typical WTG

风力发电机一般有2种运行方式：恒功率因数运行方式与恒电压运行方式。本文采用恒功率因数运行方式。设功率因数为φ，则无功功率Q= Ptan φ。

1.2 光伏发电概率模型

光伏电池的输出功率主要与光照强度有关，而光照强度受阴影、云层等因素影响，表现出了一定的随机性。考虑阴影、云层等因素后，一段时间内的光照强度r近似符合Beta分布，其概率密度函数[11]为

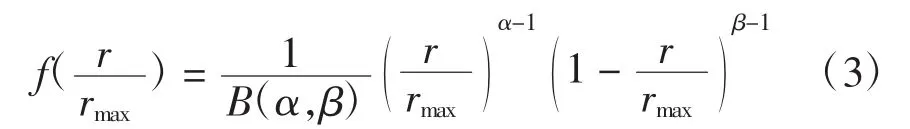
式中：rmax为该段时间内最大光照强度，W/m2；α、β为Beta分布的形状参数，其取值为正数。

若给定一个具有M个电池组件的太阳能电池阵列，则太阳能阵列总的输出功率[11]为

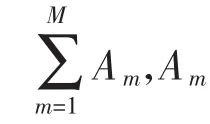
1.3 负荷概率模型

在任一指定时刻，系统的总负荷往往近似服从正态分布。此外在随机潮流中，假定负荷是正态分布的随机变量是常用的简化技术。因而设定微电网中负荷随机变量服从正态分布，有功负荷和无功负荷的概率密度函数分别为

式中：μp、μq为均值；σp、σq为方差。

2 微电网电源优化配置模型

2.1 目标函数

微电网电源优化配置的目标应是在满足系统可靠性约束的情况下，年等值投资费用最小。其中，投资费用包括设备安装费用、运行维护费用、燃料费用以及环境成本等。其目标函数为

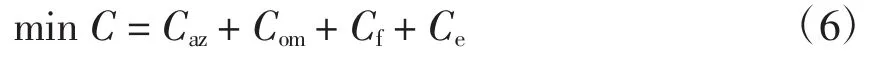
式中：Caz为年等值设备投资费用；Com为年运行维护费用；Cf为年燃料费用；Ce为环境成本。

年等值设备投资费用Caz的计算式为

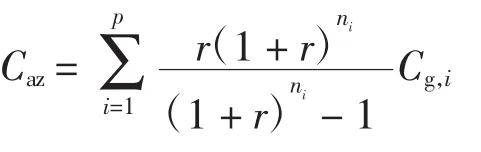
式中：Cg，i为第i个电源的装机成本；ni为第i个电源的使用年限；r为年利率。

年运行维护费用Com与各类电源的装机容量有关，计算公式为

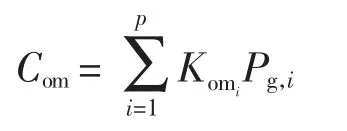
式中，Komi为第i个电源运行维护费用与容量的比例系数，元/kW。

燃料费用的计算公式为

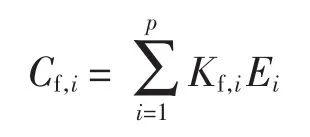
式中：Ei为第i个电源发电量，kW·h；Kf，i为电源燃料费用比例系数，元/（kW·h）。由于风能与太阳能均为可再生能源，因此风机与光伏电池的燃料费用均为0。

对于环境效益的计算，本文参考了文献[6]中不同电源污染物排放数据及环境标准，如表1和表2所示。

表1 不同微电源污染物排放数据Tab.1Pollutant emission of DG g（/kW·h）

表2 电力行业污染物环境评价标准Tab.2Environmental evaluation standard of pollutant emission in power industry 元/kg

根据表1和表2折算出微型燃气轮机环境成本系数约为0.028元/（kW·h），风机与光伏电池环境成本均为0。

2.2 约束条件

等式约束主要考虑系统功率的平衡，即

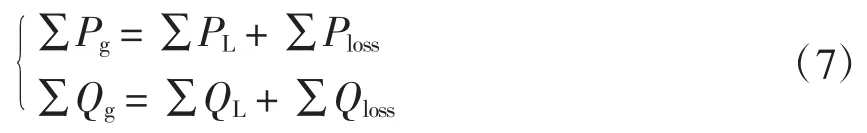
不等式约束主要考虑各节点电压水平，约束条件为

式中，uimax、uimin分别为节点i电压上限、下限。

3 考虑随机特性的微电网电源优化配置方法

常见微电网电源如风能、太阳能的输出功率与自然条件密切相关，使微电网系统运行具有随机特性，用确定性潮流算法计算相关指标具有一定的局限性，因此本节采用随机潮流计算电压越限率等指标。针对上节提出的微电网电源优化配置模型，采用粒子群算法求解该优化问题。

3.1 考虑随机特性的微电网随机潮流计算方法

根据微电网电源的概率模型，利用蒙特卡洛法模拟可以产生大量电源输出的数据，将这些数据代入到确定性潮流算法中，即可实现微电网的随机潮流计算。通过计算得出一定时间内各节点电压的越限率δi。

主要步骤如下：

步骤1读入数据，包括微电网各节点、支路参数，电源出力的概率密度函数等；

步骤2根据电源出力的概率密度函数，用蒙特卡洛法产生随机数；

步骤3根据所得电源出力随机数，对微电网进行确定性潮流计算，算出各节点电压值；

步骤4若模拟次数小于设定值，则重复步骤2；否则结束。

步骤5计算各节点电压越限率δi。

整个流程如图2所示。

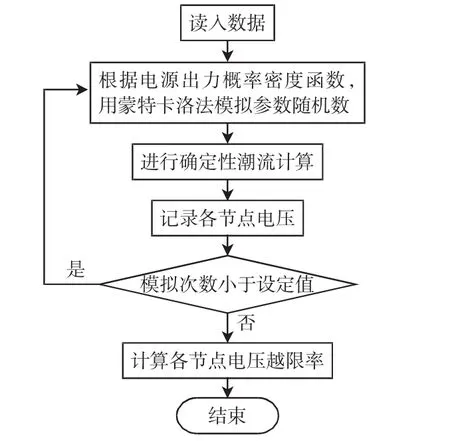
图2 蒙特卡洛法计算微电网各节点电压越限率流程Fig.2Flow chart of node voltage outrange rate in microgrid based on Monte Carlo method calculation

3.2 粒子群算法

粒子群优化PSO（particle swarm optimization）算法是近年来发展起来的一种新的进化算法[12]。它从随机解出发，迭代寻找最优解，以适应度为标准判断解的品质，通过追随当前搜索到的最优值来寻找全局最优，具有概念简明、实现容易、收敛快、精度高等特点。

粒子群算法中的每个解称之为“粒子”，所有的粒子都对应着一个与目标函数相关的适应值，每个粒子还具有速度决定它们取值的方向与距离，从而可以追踪当前最优粒子。每一次迭代中，粒子通过追踪两个最优值更新自己：其一为个体最优值pid，即粒子自身找到的最优解；另一个为全局最优值pgd，即整个粒子群当前的最优解。在找到两个最优值后，粒子新的速度以及位置计算式为

3.3 采用粒子群算法配置微电网电源的关键步骤

本文用粒子群优化算法求解微电网电源优化配置问题，对其中一些关键步骤进行了如下处理。

（1）初始粒子的选取。通常用粒子群算法求解优化问题时，初始粒子群设定为随机值。这种随机方式产生的初始粒子存在着一定的局限性：粒子质量参差不齐，质量较低的初值如果直接代入程序进行优化计算，会大大降低程序收敛速度，而良好的初始粒子选取，可以提高问题求解的效率。因此有必要对初始粒子进行限制及修正。本文中初始粒子的产生步骤如下。

步骤1粗略确定可行域：根据接入微电网的总负荷大小估算分布式电源接入总容量，接入总容量需大于总负荷。

步骤2根据文献[13]，在总容量相同的情况下，分布式电源分散在各个节点对系统电压的支撑作用比集中在同一节点时大；从减小电压变化率的角度，分布式电源不宜接在末节点。该结论对粒子初值选取有一定的参考意义。

步骤3随机生成一个初始群体，群体中每个粒子的维度为2m，用集合表示为

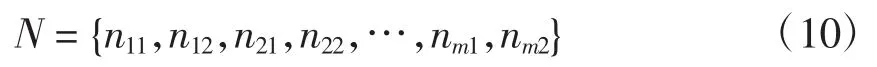
（2）约束条件的处理。为了避免算法在迭代过程中产生不满足约束条件的粒子，需要对约束条件进行处理。惩罚函数法是处理这类问题的常用方法。其基本思想是，根据约束条件制造出“惩罚项”，用来对不满足约束条件的解进行“惩罚”。将原目标函数与该惩罚项结合，拓展出新的目标函数。

本文拟采取惩罚函数法处理约束条件。考虑到约束条件对于节点电压的约束，引入节点电压越限率δ构造惩罚项。拓展后的目标函数为

3.4 算法流程

采用粒子群算法求解考虑随机特性的微电网电源优化配置问题的一般步骤如下。

步骤2按第3.3节所述方法产生可行域内的初始种群。

步骤3运用基于蒙特卡洛的随机潮流计算每个粒子的电压越限率Σδ，进而计算每个粒子的适应值f。通过比较适应值大小，得到全局最优粒子pgd、个体最优粒子pid。

步骤4根据式（9）更新粒子信息，得到粒子新的位置与速度。

步骤5判断迭代次数是否达到设定值，若小于设定值，返回步骤3，否则结束，输出当前pgd即为最优解。

算法流程如图3所示。

图3 基于PSO算法的微网电源优化配置问题求解流程Fig.3FlowchartofoptimizingDGbasedonPSOalgorithm

4 算例与结果分析

本文所用算例选自文献[14]，对原算例做了改动，修改后的系统结构图如图4所示，图中数字为节点编号，假设系统只允许在2、3、7、11节点接入分布式电源。

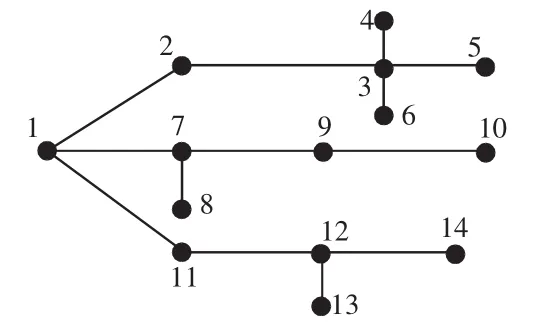
图414 节点微网算例系统结构Fig.4Strucure of a 14-node microgrid system

所用风力发电机参数如表3所示，光伏电池参数如表4所示[15]。

表3 风力发电机参数Tab.3Parameters of WTG

表4 光伏电池参数Tab.4Parameters of PV cells

根据本文第1节的概率模型仿真得到的某次年风速曲线如图5所示，年光照强度曲线如图6所示，有功负荷曲线如图7所示，可见采用本文概率模型可以很好地模拟出微电网所在地区的实际自然条件以及负荷水平。

图5 微电网所在地区年风速曲线仿真Fig.5Simulation of annual wind velocity at the location of microgrid

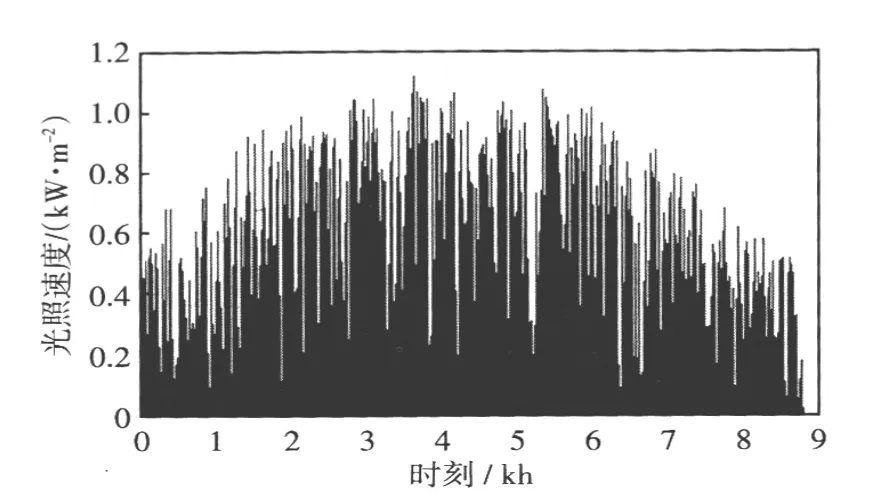
图6 微电网所在地区年光照强度仿真Fig.6Simulation of annual sunlight intensity at the location of microgrid

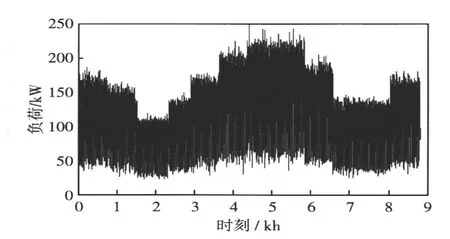
图7 微电网所在地区总有功负荷仿真Fig.7Simulation of annual real load at the location of Microgrid

采用本文所提方法求解微电网电源优化问题。

设定年利率r为6%，电源使用年限为20年，则年资金回收率为8.72%。各类电源的基本成本参数[5，14]如表5所示。

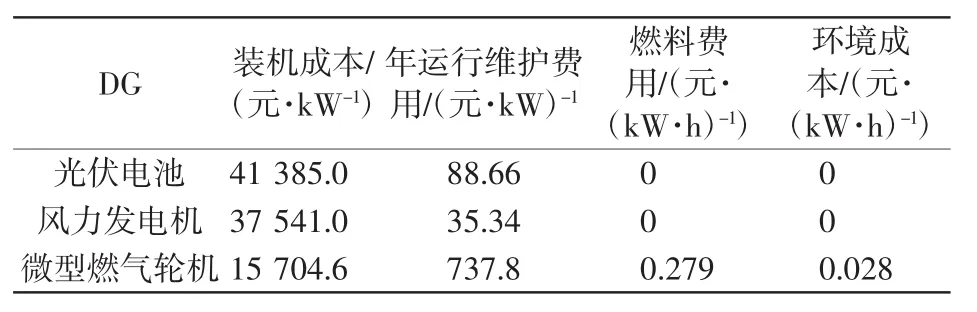
表5 微电网电源成本参数Tab.5Cost information of DG in a Microgrid

惩罚因子Kv初始值设为108，当电压越限率超过0.01时为109。粒子群的规模设定为15，最大迭代次数40，加速度常数c1=c2=2，惯性权重ω=0.7。得到的微电源最优配置方案如表6所示。该方案下各节点电压越限率与年越限小时如表7所示。

表6 微电网电源最优配置方案Tab.6Scheme of optimal siting and sizing of DG

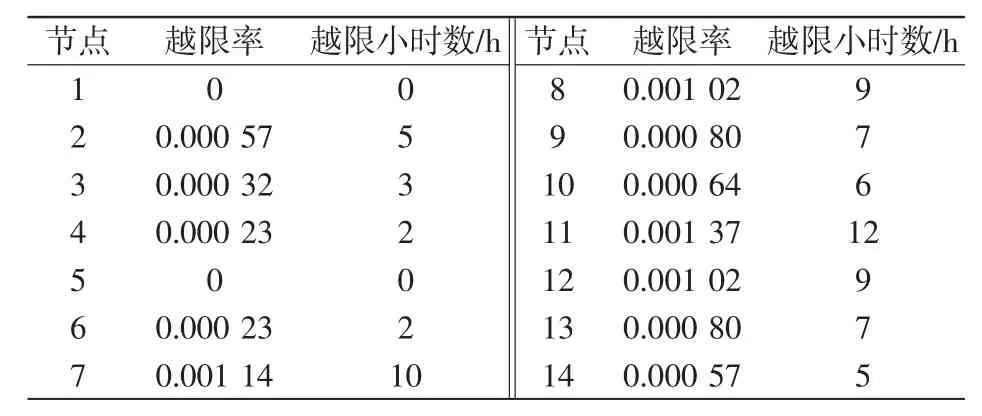
表7 最优方案下微电网节点电压指标Tab.7Voltage indices of Microgrid under optimal scheme

表8列出了另一种配置方案（以下称为方案2），该方案与最优方案（以下称为方案1）各节点装机容量几乎相同，区别是减少了光伏电池的比例，增加了风机的比例。方案2的节点电压指标如表9所示，可见其节点电压越限率明显高于方案1。

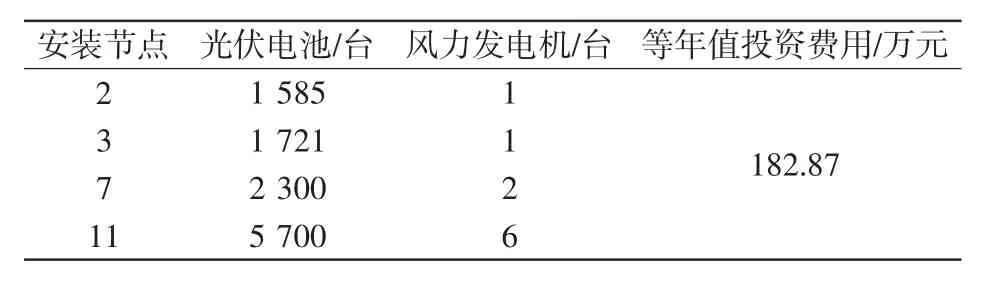
表8 微电网电源配置方案2Tab.8Scheme 2 of siting and sizing of DG

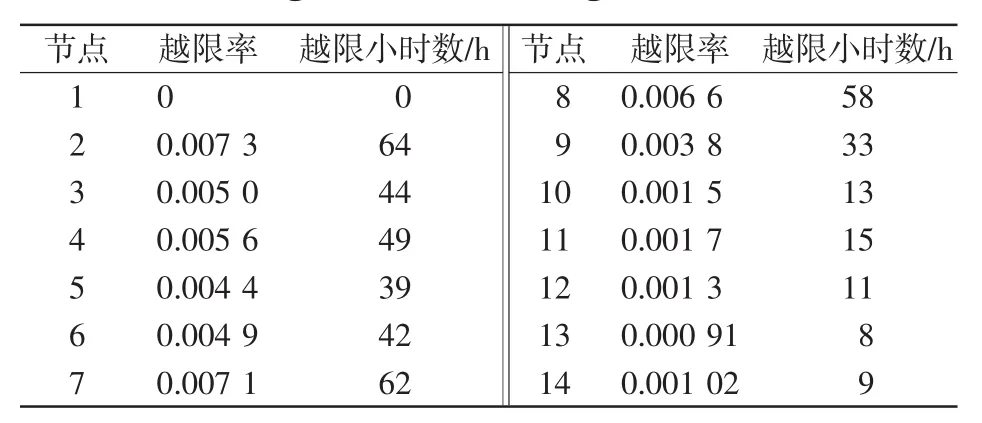
表9 方案2微电网节点电压指标Tab.9Voltage indices of Microgrid under scheme 2

图8列出了两种方案平均节点电压的对比。

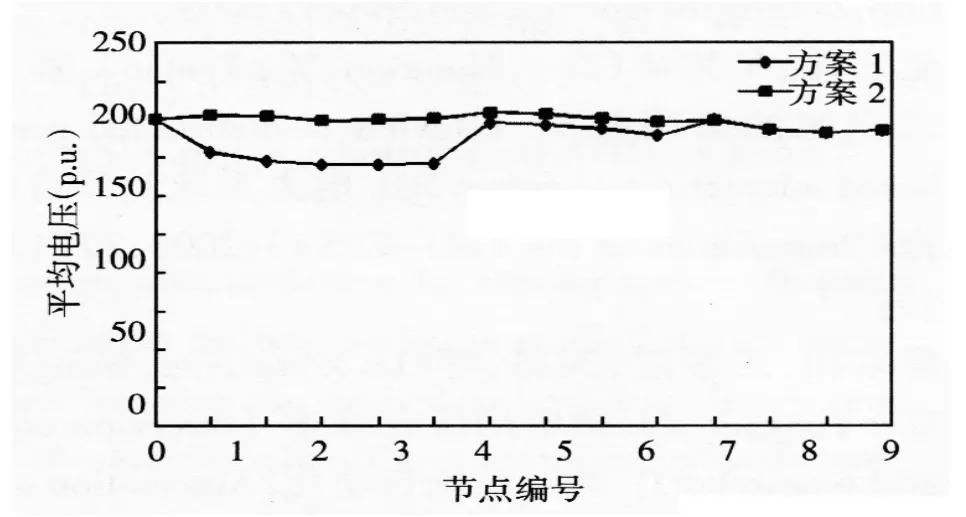
图8 不同配置方案下节点电压对比Fig.8Contrast of average node voltage under different schemes

通过对照发现方案2的节点平均电压明显高于方案1。经分析，这是由于方案2风力发电机出力过多造成的，算例中光伏发电的输出功率与负荷变化趋势基本一致，而风机输出功率则与负荷变化存在一定差异，尤其是负荷较低（如凌晨时分）时，风机输出功率容易过剩，从而导致节点电压偏高。可见，在配置电源时需要根据负荷情况，合理分配光伏电池与风机的比例，否则容易导致电压指标不合格。

5 结语

本文建立了以微电源类型、接入位置与容量为待求变量，以综合经济成本最低为目标函数，以微电网节点电压作为主要约束条件的全年孤岛运行微电网的电源优化配置数学模型，使用粒子群算法解决了微电网电源配置问题。其中，电压约束条件转化为节点电压越限率衡量，考虑了风能、太阳能等电源的随机性、波动性等特点，采用蒙特卡洛法计算电压指标。

算例表明，使用该方法对微电网电源进行配置，可以在控制投资成本的同时，有效地将节点电压越限率控制在较低水平，满足了经济性和可靠性的要求。

针对风能、太阳能等随机性特征明显的特点，采用蒙特卡洛法模拟仿真直观、方便。为了使仿真结果更准确，需要更加精确的概率分布模型；同时蒙特卡洛法需要模拟大量的数据，导致计算时间较长，因此需要提高蒙特卡洛法模拟的效率；这些都是后续研究需要完善的地方。

[1]Lasseter R，Abbas A，Marnay C.Integration of distributed energy resources：the CERTS microgrid concept[EB/OL]. http：//certs.lbl.gov/pdf/50829.pdf，2003．

[2]赵宏伟，吴涛涛（Zhao Hongwei，Wu Taotao）.基于分布式电源的微网技术（Review of distributed generation based microgrid technology）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2008，20（1）：121-127.

[3]鲁宗相，王彩霞，闵勇，等（Lu Zongxiang，Wang Caixia，Min Yong，et al）.微电网研究综述（Overview on microgrid research）[J].电力系统自动化（Automation of Electric Power Systems），2007，31（19）：100-107.

[4]张建华，黄伟.微电网运行控制与保护技术[M].北京：中国电力出版社，2010.

[5]马溪原，吴耀文，方华亮，等（Ma Xiyuan，Wu Yaowen，Fang Hualiang，et al）.采用改进细菌觅食算法的风/光/储混合微电网电源优化配置（Optimal sizing of hybrid solar-wind distributed generation in an islanded microgrid using improved bacterial foraging algorithm）[J].中国电机工程学报（Proceedings of the CSEE），2011，31（25）：17-25.

[6]崔弘，郭熠昀，夏成军（Cui Hong，Guo Yiyun，Xia Chengjun）.考虑环境效益的分布式电源优化配置研究（Research on optimal allocation of distributed generation by considering environmental benefits）[J].华东电力（East China Electric Power），2010，38（12）：1968-1971.

[7]刘波，张焰，杨娜（Liu Bo，Zhang Yan，Yang Na）.改进的粒子群优化算法在分布式电源选址和定容中的应用（Improved particle swarm optimization method and its application in the siting and sizing of distributed generation planning）[J].电工技术学报（Transactions of China Electrotechnical Society），2008，23（2）：103-108.

[8]伍言，刘俊勇，刘友波，等（Wu Yan，Liu Junyong，Liu Youbo，et al）.基于负荷组合与光伏电源匹配算法的微电网配置（Microgrid configuration based on matching algorithm between load combination and photovoltaic DG）[J].华东电力（East China Electric Power），2012，40（1）：51-55.

[9]别朝红，刘辉，李甘，等（Bie Chaohong，Liu Hui，Li Gan，et al）.含风电场电力系统电压波动的随机潮流计算与分析（Voltage fluctuation of a power system with wind farms integrated by probabilistic load flow）[J].西安交通大学学报（Journal of Xi'an Jiaotong University），2008，42（12）：1500-1505.

[10]Ghahderijani M M，Barakati S M，Tavakoli S.Reliability evaluation of stand-alone hybrid microgrid using sequential Monte Carlo simulation[C]//Iranian Conference on Renewable Energy and Distributed Generation.Tehran，Iran：2012．

[11]王敏（Wang Min）.分布式电源的概率建模及其对电力系统的影响（Research on the Probabilistic Modeling of Distributed Generation and its Influences on Power Systems）[D].合肥：合肥工业大学电气与自动化工程学院（Hefei：School of Electrical Engineering and Automation，Hefei University of Technology），2010.

[12]Kennedy J，Eberhart R.Particle swarm optimization[C]// IEEE International Conference on Neural Networks.Perth，Australia：1995．

[13]王志群，朱守真，周双喜，等（Wang Zhiqun，Zhu Shouzhen，Zhou Shuangxi，et al）.分布式发电对配电网电压分布的影响（Impacts of distributed generation on distributed system voltage profile）[J].电力系统自动化（Automation of Electric Power Systems），2004，28（16）：56-60.

[14]石庆均（Shi Qingjun）.微网容量优化配置与能量优化管理研究（Research on Optimal Sizing and Optimal Energy Management for Microgrid）[D].杭州：浙江大学电气工程学院（Hangzhou：College of Electrical Engineering，Zhejiang University），2012.

[15]赛维LDK公司.020P组件技术规格书[EB/OL].http：// www.ldksolarpower.com/mod_l.php，2012.

Optimal Siting and Sizing of Distributed Generation Planning in Microgrid by Considering Stochastic Characteristic

LU Yang1，LU Jin-ling1，2，SHI Shao-tong1，YANG Ren-gang2
（1.School of Electrical and Electronic Engineering，North China Electric Power University，Baoding 071003，China；2.College of Information and Electrical Engineering，China Agriculture University，Beijing 100083，China）

Optimal siting and sizing of distributed generation（DG）planning in a stand-alone microgrid is an important issue to make microgrid operate reliably and economically.In this paper a mathematical model for optimal sizing of DG was established.The model took types，sites and sizes of DG as the variables，minimum overall cost as the objective function and node voltage as the constraints.The particle swarm optimization algorithm was proposed to solve the optimization problem.As the common DG such as wind and solar energy have the characteristics of randomness and waviness，Monte Carlo method was used to simulate DG's characteristics based on probability distribution model of different types of DG.Combining with the deterministic power flow method，a probabilistic power flow method was established.This method was used to judge whether the node voltage of microgrid was out of range under certain DG configuration.A case study shows that，using this method to configure DG can both control costs and make the node voltage in a proper range，which can meet the needs of economy and reliability.

microgrid；stand-alone mode；particle swarm optimization；optimal sizing of distributed generation；probabilistic power flow

TM61；TM743

A

1003-8930（2013）03-0108-07

卢洋（1988—），男，硕士研究生，研究方向为电力系统运行、分析与控制。Email：ppyyang@qq.com

2012-12-22；

2013-02-04

国家高技术研究发展计划（863计划）资助项目（2012AA050217）

卢锦玲（1971—），女，博士，副教授，研究方向为电力系统运行、分析与控制。Email：lujinling@126.com

石少通（1988—），男，硕士研究生，研究方向为电力系统运行、分析与控制。Email：877702658@qq.com