包括供电瓶颈识别的电力系统供电能力评估

李力，李剑辉，高超，杨燕，郭文涛，文福拴

（1.广东电网公司电力调度控制中心，广州 510601；2.华南理工大学电力学院，广州 510640；3.浙江大学电气工程学院，杭州 310027）

包括供电瓶颈识别的电力系统供电能力评估

李力1，李剑辉1，高超1，杨燕2，郭文涛2，文福拴3

（1.广东电网公司电力调度控制中心，广州 510601；2.华南理工大学电力学院，广州 510640；3.浙江大学电气工程学院，杭州 310027）

供电能力评估不仅是计算量度指标，更是为系统运行和规划人员提供供电瓶颈环节等重要信息。现有方法尚不能系统而有效地处理这些问题。在此背景下，为了评估电力系统供电能力，构造了供电裕度价值函数来引导负荷在系统中节点间合理分配，并同时识别系统运行中存在的供电瓶颈。首先，以供电裕度价值函数最大化为目标，考虑系统安全运行约束，构造了供电能力分析评估的数学模型；然后，采用差异进化算法求解所发展的优化问题；最后，通过在广东电力系统的实际应用验证了模型和方法的可行性与有效性。

电力系统；供电能力；供电瓶颈识别；价值函数

电力系统最大供电能力TSC（total supply capability）是指一定供电区域内配电网满足N-1安全准则以及各种实际运行约束下的最大负荷供应能力[1，2]。通常用供电裕度（load supply margin）来评价网络承受负载的能力。

最大供电能力和供电裕度是衡量电力系统运行安全性与经济性的重要指标，对电力系统优化规划与运行管理方面具有重要意义。随着电力系统规模的不断扩大和运行复杂性的逐步增加，电力系统供电能力的评估分析不再仅局限于计算指标供电能力和供电裕度，更希望在计算过程中能够及时、准确地发现系统中制约供电能力的关键瓶颈，为网络规划、建设和运行决策提供切实可信的参考信息。

本文引入供电裕度价值函数作为供电能力评估分析的目标函数。在所定义的供电裕度价值函数中，价值函数系数随供电裕度变化，这样就可以通过优化整体供电裕度来控制负荷的合理分配，在此基础上构建了供电能力评估的优化模型；然后，采用差异进化算法对所发展的优化模型进行求解得到供电裕度，并算得最大供电能力；最后，用广东电力系统的实际数据验证了所发展的模型和方法的可行性与有效性。

1 现有电力系统最大供电能力分析方法

现有的电力系统最大供电能力分析方法主要分为解析法和优化方法两大类。

解析法[3～5]是将电力系统供电能力表达为网络参数的函数，通过简单的计算即可得出供电能力和供电裕度。文献[3，4]将供电能力视为变电站变电能力的函数；文献[5]主要从短路电流角度出发，分析了供电能力与主变参数间的关系。解析法简单，便于计算，有比较明确的物理意义，但计算结果过于粗糙，往往无法充分考虑发输电设备对供电能力的影响。这类方法一般仅用作对供电能力的初步定性分析。

优化方法则是将供电能力计算问题描述为一个带约束的数学优化模型，采用合适的优化算法或启发式方法，如线性规划法、重复潮流法和信赖域法等[1，6～8，15]求解。优化方法能够充分考虑系统中的各种物理约束，处理方式灵活，在实际电力系统中得到了较为广泛的应用。优化方法中的目标函数主要采用下述两种方法确定。

（1）假设系统中所有负荷均按同一比例λ增长，则相应的优化目标为max{λ}[1]。这样的优化目标与实际负荷增长情况较为吻合，但却存在着无法充分发掘瓶颈环节和计算结果过于保守的问题。

以如图1所示的简单系统为例来说明这种方法。假设当λ=1.05时，支路B4过载，则停止增加负荷，即可得出供电裕度大小。此时负荷节点L1～L4的供电裕度均为5%。然而，将B4作为图1所示系统的瓶颈环节是不合理的，B4只是制约了节点L4的供电裕度，若网络中其余设备仍有裕度，则节点L1～L3的负荷可继续增长。因此，基于比例系数的优化方法往往并不能真实地反映电力系统各个负荷节点的供电裕度，也不能准确地识别瓶颈环节。

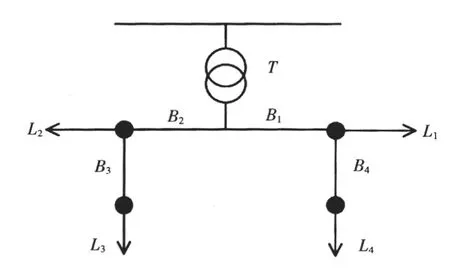
图1 系统接线示意Fig.1Sketch of system wiring

（2）以最大化网络中所有负荷点有功负荷功率之和作为优化目标[6～8]。采用这类优化目标时，会发生误判供电瓶颈和对负荷节点供电能力评估结果不准确的问题。仍以图1所示系统为例进行说明。当以负荷节点有功功率总和最大化作为优化目标时，负荷节点L1和L2上各增加50 MW负荷和节点L1上单独增长100 MW负荷对于优化目标的效果是等价的。因此，在计算结果中可能出现节点L1的供电裕度较大而L2的供电裕度偏低的情况。这实际上并不是因为网络设备容量约束引起的，而是由于优化过程中负荷增长模式不合理导致的。这样的结果不仅无法为系统运行规划人员提供有效信息反而可能造成判断混乱。

从上述可知，当采用基于比例系数的优化方法时，可能出现不能真实反映各个负荷节点供电裕度和不能准确识别供电瓶颈的问题；当以最大化网络中所有负荷点有功负荷功率之和作为优化目标时，会由于假设的负荷增长模式与实际情况不一致而导致误判供电瓶颈。只有能够合理描述负荷增长模式，才有可能准确识别供电瓶颈。

2 供电裕度价值函数

2.1 价值函数

价值函数[9]（value function）的概念源于经济学领域，通过函数参数（即函数形式和其系数）来描述决策者对收益/风险的反应（类似于对风险/收益的偏好程度）及其灵敏程度，目前在风险决策[10]、综合评价[11]等方面获得了比较成功的应用。常用的价值函数包括比例函数、U形函数和分段函数等。

将价值函数应用于度量供电裕度问题时，供电裕度相当于决策收益或风险，而价值函数则表示对系统安全和经济运行的影响。

1.2 供电裕度的价值函数

里选用比例形式的价值函数作为负荷节点供电裕度的价值函数，有

这式中：Qi、ωi和Li分别为节点i的供电裕度的价值量、价值函数系数和供电裕度。

当ωi为常数时，供电裕度的价值函数形式如图2所示。

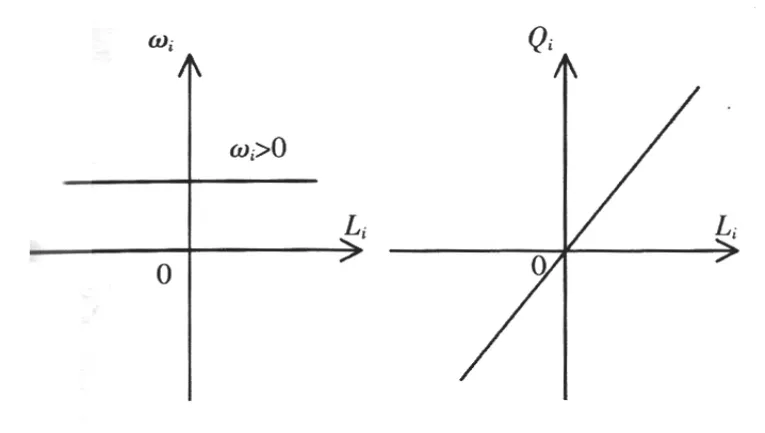
图2 ωi＞0且为常数时的价值函数曲线Fig.2Curve of the value function when ωiis a positive constant

在实际电力系统中，供电裕度并不是越大越好，过大的供电裕度在一定程度上说明资源浪费和分配不合理。供电裕度为负值说明系统已运行在不安全状态，需要调整。为此，这里采用如图3所示的分段线性函数来描述ωi。

图3 价值函数系数ωiFig.3Curve of ωi

图3所示的分段线性函数的物理意义可从下述两个方面说明。

（1）当供电裕度大于零时，价值函数取值大于零；供电裕度越大，价值函数取值越大。不过，随着供电裕度增大，其单位增长所引入的价值量越来越小。

（2）当供电裕度小于零时，价值函数取值小于零；供电裕度越小，价值函数取值越小，且随着供电裕度减小，其单位减小所引入的价值量减小的越明显。当供电裕度小于零时，系统已处于不安全状态，其绝对值越大，偏离安全临界点越远，运行人员对风险的敏感性就越高。

电力系统整体供电裕度价值函数可表示为

式中，K为系统中包含的负荷节点数目。

如此定义的供电裕度价值函数能够合理考虑不同区段内的供电裕度对电力系统运行的实际价值，并避免节点间的不合理负荷增长。

3 供电能力评估数学模型

基于供电裕度价值函数的供电能力评估问题可描述为目标函数最大化问题。

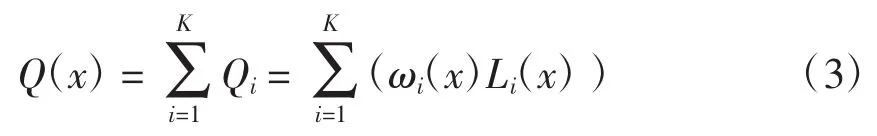
式中，x为决策变量，表示各负荷节点的有功功率。

如前所述，以供电裕度价值函数作为优化目标获得的最优解可以使得各负荷节点供电裕度分布比较均匀，并可避免采用比例增长系数法时评估结果过于保守和不能准确找到输电瓶颈的问题。与文献[2，14]相比较，本文相对偏重于经济性，更接近于实际运行需要，且目标函数构造方法较为简单，同时由于价值函数系数可随着供电裕度变化，故本文的方法更加灵活；文献[2]将各主变负载率方差最小作为单一优化目标，灵活性偏低，经济性需要商榷。文献[14]在确定联络通道组的临界容量时，先采用线性规划的方法获得最大供电能力，该值可能偏于保守或不准确，之后通过区间逼近方法获得临界容量，即需依赖最大供电能力才能发掘供电瓶颈，可靠性需进一步验证。

约束条件主要包括潮流约束、支路容量约束和节点电压幅值约束等。

1）潮流约束

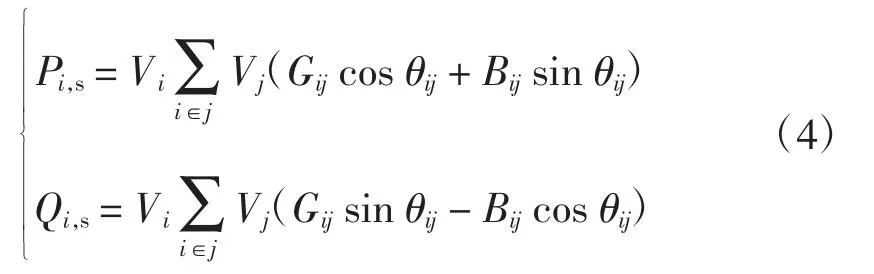
式中：Pi，s和Qi，s分别为节点i的有功注入量和无功注入量；Vi和Vj分别为节点i和节点j的电压幅值；i∈j表示所有与节点i直接相连的节点，包括j=i；Gij和Bij分别为节点导纳矩阵相应的实部和虚部；θij为支路ij两端节点电压的相角差。

2）支路安全约束

本文所述支路包括线路及变电站主变压器等，其约束包括基态和N-1预想事故两种情况下的安全约束。

基态情况下支路不过载约束可表示为

N-1预想事故情况下支路不过载约束表示为

3）节点电压幅值约束

本文节点电压幅值约束包括基态和N-1预想事故两种情况下的幅值约束。

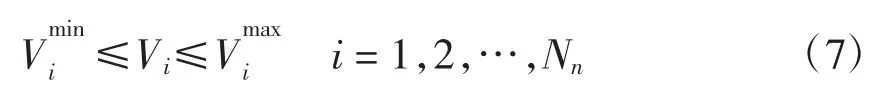
4）发电机组出力约束

式（3）～式（8）构成了供电能力评估的数学模型。

4 求解算法

采用差异进化算法DE（Differential Evolution）求解所发展的优化模型。DE算法与其他一些现代启发式优化算法如遗传算法相比，适应性更强，且在电力系统多个领域中都取得了较为成功的应用[12，13]。

4.1 适应度函数合成

式（4）和式（8）所表示的约束条件可通过潮流计算和机组出力状态来判断。对于违反式（5）～式（7）的运行方案，总越限量的计算公式为

式中：Hi（x）为节点i电压幅值约束的越限项；Gj（x）为支路j有功潮流约束的越限项；qi和pj为反应节点i和支路j重要程度的权重系数，可以根据对节点和支路的重视程度确定，这里是根据节点供电负荷大小和支路潮流大小确定的；li（x）和lj（x）分别为节点i电压幅值和支路j有功潮流的越限程度。

用DE求解时，适应度函数可表示为

4.2 求解流程

采用DE算法求解上述最大供电能力评估模型的步骤如下。

步骤1输入原始数据，包括设备容量参数、发电设备生产状态等。

步骤2设置算法参数，如最大迭代次数kmax、种群规模NS、交叉概率F和变异概率s等。

步骤3采用随机方法生成初始种群，设置迭代次数k=1。

步骤4对于初始种群中的每个个体，计算相应的目标函数Qi，i=1，2，…，m，检验其是否满足约束。对不满足约束的个体，按式（9）计算总越限量Hi，i=1，2，…，m，用式（10）得到适应度fi。

步骤5进行交叉和变异操作，产生第k次迭代的子代种群。在DE算法中，通过交叉和变异产生第k代子代种群中的每个个体。

步骤6根据第k次迭代的子代种群中每个个体所代表的负荷水平，修改相应机组出力，进行安全校验，逐一计算第k次迭代的子代个体的适应度fi。

步骤7在当前2NS个个体中挑选出NS个个体作为第k+1次迭代的父代种群。挑选原则为

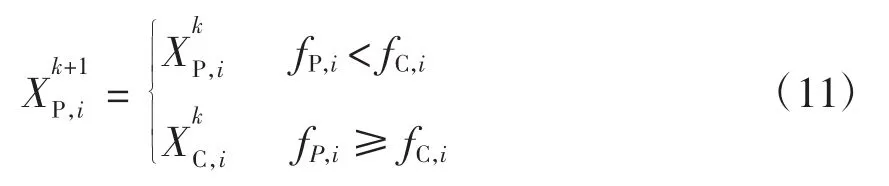
步骤8若k〉kmax，则中止迭代；否则，令k=k+1，转入步骤6。

步骤9输出最终结果。

5 算例分析

基于上述模型和方法在Visual Studio 2005平台上开发了软件系统。为了满足电力调度部门实际分析需要，把供电能力计算分为单个500 kV变电站片区分析模式和包含多个500 kV变电站的地区分析模式。

以广东电力系统2011年高峰负荷水平运行方式为例对所提模型和方法进行验证。这里给出2个算例：第1个算例针对顺德站供电片区，仅包括1个500 kV变电站；第2个算例针对广州地区，包括多个500 kV变电站。

5.1 顺德站供电片区

顺德站供电片区接线如图4所示，共包括6个220 kV供电变电站和1个本地电厂，供电负荷为2 235 MW。

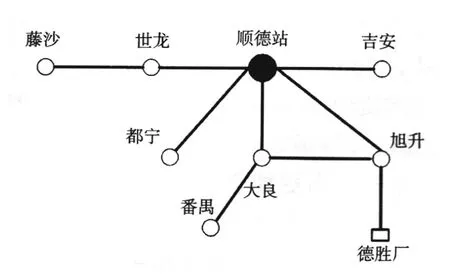
图4 顺德站供电片区接线Fig.4Wiring of Shunde power supply area

应用所提模型和方法求得该片区整体最大供电能力为2 601.63 MW，供电裕度为14.09%。各220 kV负荷站点的供电能力和供电裕度如表1所示。

由表1可见，受到顺德站500 kV下送主变容量约束，该片整体供电裕度水平偏低（旭升由于有德胜厂供电，供电裕度水平相对其它站点较高）。此外，顺德-世龙线在N-1预想事故下输电容量基本已无裕度。大良站的供电潮流主要由番禺-大良线、旭升-大良线提供，在基态负荷下番禺-大良线安全裕度已偏低，这也是制约大良站供电能力的一个关键因素。

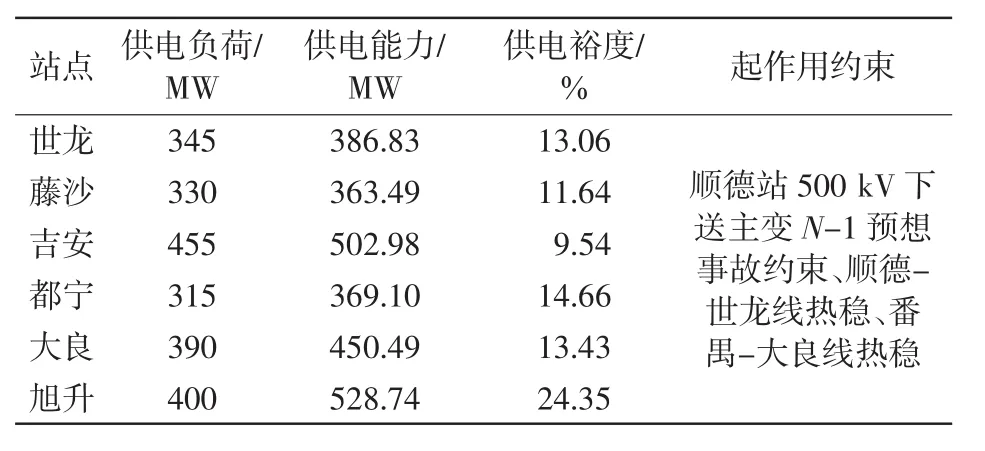
表1 顺德站供电片区各负荷站点供电能力和供电裕度Tab.1Load supply capability and load supply margin at each load bus of Shunde power supply area

在对电力系统进行优化调度时，应对这些因素进行协调处理，不仅要提高系统整体供电能力，也需要适当考虑容量资源在各个站点间的合理分配。

3.2 广州地区

广州地区是广东电力系统最为重要的负荷中心之一，主要包括5个500 kV供电片区，如图5所示。在2011年高峰负荷水平下，其供电负荷达到11 000 MW以上，供电压力较大。

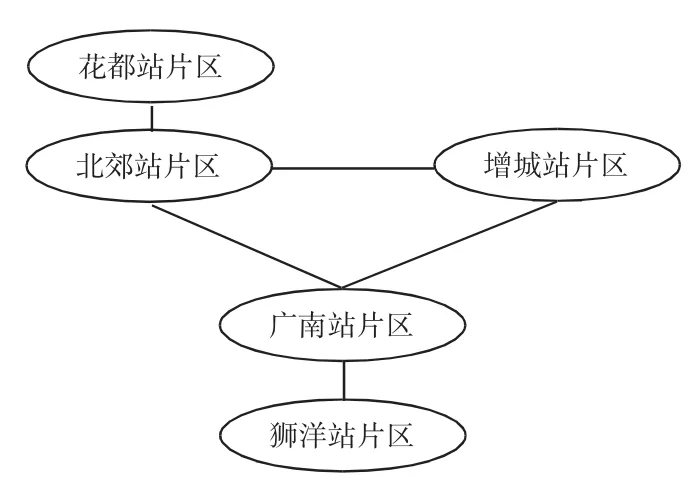
图5 广州地区500 kV供电片区Fig.5Connection structure of the 500 kV power supply area in Guangzhou

各片区整体供电能力和供电裕度评估结果如表2所示，各220 kV站点的供电能力和供电裕度指标如表3所示。

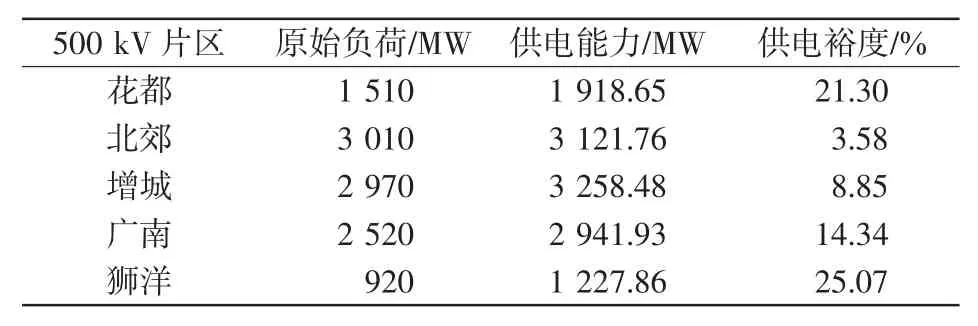
表2 广州地区各供电片区整体供电能力和供电裕度Tab.2Load supply capability and load supply margin at each power supply section in Guangzhou

由表3可知，花都片区供电瓶颈为花都站下送500 kV主变，该片区的220 kV输电设备尚具有较大安全裕度，因此该片区各220 kV变电站供电能力和供电裕度指标分布较为均匀。北郊站供电片区出现供电瓶颈的主要原因在于本地220 kV线路容量不足，如由于北郊-石井线热稳约束，石井甚至无法完成供电任务（供电裕度小于零）。同样地，北郊-犀牛线热稳约束也造成了北郊-犀牛-麒麟-天河-鹿鸣B供电路径上的供电裕度水平普遍偏低，甚至出现负值。增城站A母线片区主要是受到增城-棠下线容量制约，造成棠下、潭村、天河供电裕度水平偏低，而500 kV下送主变资源只能向宁西站上分配，受到这两方面因素影响，宁西站供电裕度水平较高。而增城B母线片区的整体供电能力受到500 kV主变变电容量约束，各站点供电裕度分配较为均匀。广南片起作用约束主要为广南-瑞宝线热稳约束，因此该供电路径上的站点供电裕度水平较低，而其余站点具有较高的供电裕度。

通过以上分析可以发现，若瓶颈环节为500 kV下送主变容量，则该片区各负荷节点供电裕度分布一般较为均匀；若瓶颈环节为本地输电线路，该线路供电路径上的负荷站点供电裕度一般相对于该片区其它站点较低，如增城A母线片区宁西供电裕度水平明显高于增城-棠下供电路径上负荷节点的供电裕度。虽然从运行的角度看，过高的供电裕度可能并不符合实际负荷分布，但这样的差异性供电裕度能给予运行规划人员两个方面的信息。

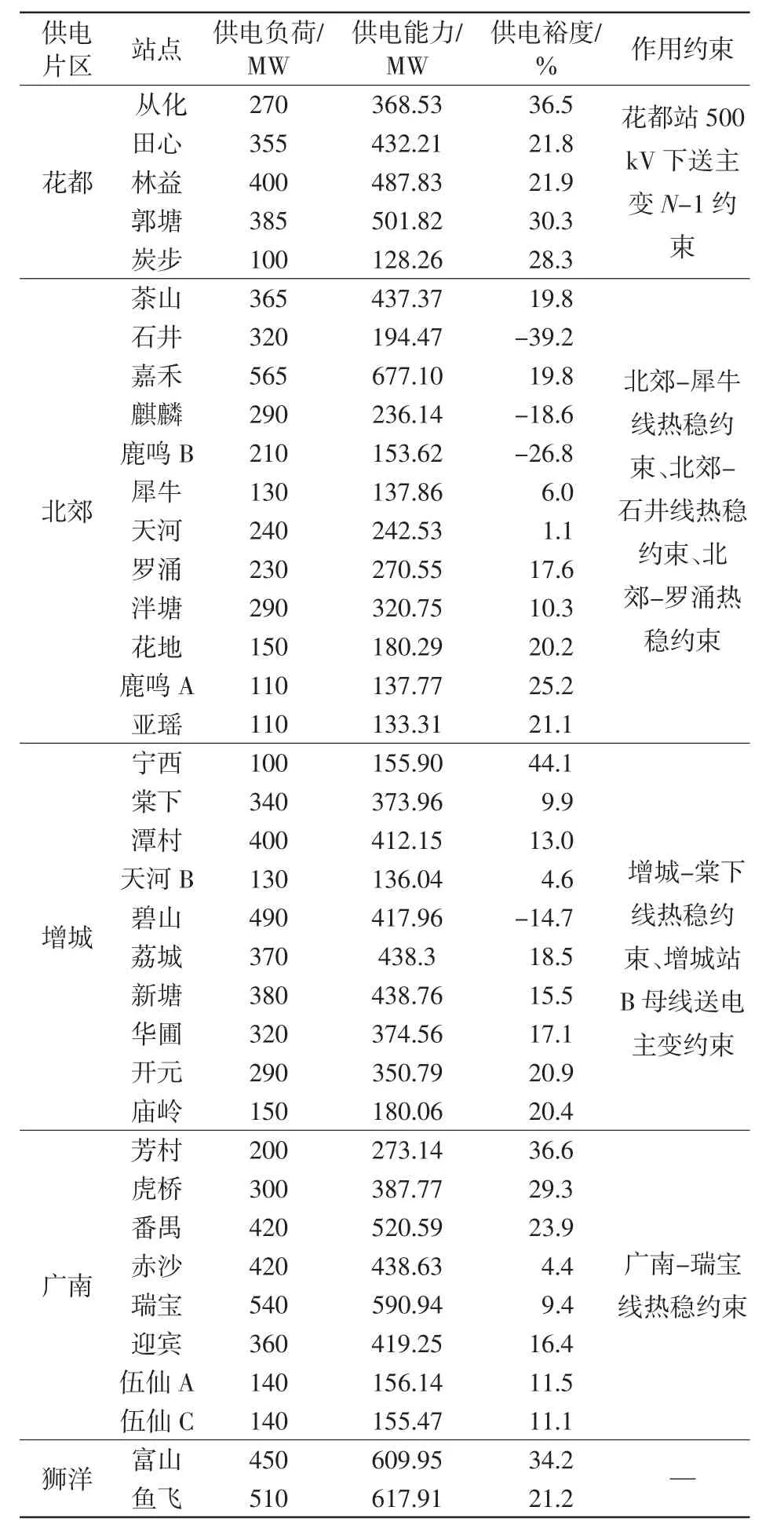
表3 广州地区各负荷站点供电能力和供电裕度Tab.3Load supply capability and load supply margin at each load bus in Guangzhou

（1）同一片区不同负荷站点供电裕度差异很大在相当程度上说明本地输电资源分配不合理，需要从规划层面上考虑这一问题。

（2）对于暂时无条件进行线路扩容建设的场合，这样的差异性供电裕度也能为转移负荷等运行措施提供参考信息。

6 结论

以最大化系统供电裕度价值作为优化目标，构建了包括供电瓶颈识别的最大供电能力评估分析方法。较之于直接以等比例负荷增长或节点负荷功率之和为基础的优化方法，本文所发展的方法具有以下优点。

（1）能够准确发现系统中存在的瓶颈环节。

（2）通过价值函数的引导，能够在评估分析中使负荷的增长分布更加符合实际负荷分布，从而使评估结果更为合理。

（3）求得的供电能力和供电裕度包含了更多的实用信息，可为电力网络规划、负荷转移等提供更加直接和有用的依据。

通过在广东实际电力系统中的应用，证明了所发展的模型和算法的可行性与有效性。

[1]Xiao J，Li F，Gu W Z，et al.Total supply capability and its extended indices for distribution systems：definition，model calculation and applications[J].IET Generation，Transmission and Distribution，2011，5（8）：869-876.

[2]肖峻，谷文卓，郭晓丹，等（Xiao Jun，Gu Wenzhuo，Guo Xiaodan，et al）.配电系统供电能力模型（A supply capability model for distribution systems）[J].电力系统自动化（Automation of Electric Power Systems），2011，35（24）：47-52.

[3]王成山，罗凤章，肖峻，等（Wang Chengshan，Luo Fengzhang，Xiao Jun，et al）.基于主变互联关系的配电系统供电能力计算方法（An evaluation method for power supply capability of distribution system based on analyzing interconnections of main transformers）[J].中国电机工程学报（Proceedings of the CSEE），2009，29（13）：86-91.

[4]罗凤章，王成山，肖峻，等（Luo Fengzhang，Wang Chengshan，Xiao Jun，et al）.一种简捷实用的配电系统供电能力计算方法（A simple and practical method to evaluate power supply capability of distribution system）[J].电网技术（Power System Technology），2008，32（23）：56-60.

[5]马彬，姜明月，王天华（Ma Bin，Jiang Mingyue，Wang Tianhua）.220 kV分区电网与互联电网供电能力研究（Study on power supply capability of 220 kV disconnected grid and interconnected gird）[J].电网技术（Power System Technology），2008，32（S1）：1-4.

[6]李红军，李敬如，杨卫红（Li Hongjun，Li Jingru，Yang Weihong）.基于信赖域法的城市电网供电能力充裕度评估（Assessment of urban power network power supply capability by trust region method）[J].电网技术（Power System Technology），2010，34（8）：92-96.

[7]束洪春，胡泽江，刘宗兵（Su Hongchun，Hu Zejiang，Liu Zongbing）.城市电网最大供电能力在线评估方法及其应用（Online evaluation of utmost power supply ability of urban power system and its application）[J].电网技术（Power System Technology），2008，32（9）：46-50.

[8]邱丽萍，范明天（Qiu Liping，Fan Mingtian）.城市电网最大供电能力评价算法（A new algorithm to evaluate maximum power supply capability of urban distribution network）[J].电网技术（Power System Technology），2006，30（9）：68-71.

[9]熊晶晶，史本山（Xiong Jingjing，Shi Benshan）.基于价值函数的行为风险投资组合模型研究（Research on behavioral venture capital portfolio model based on value function）[J].技术经济（Technology Economics），2011，30（2）：66-70.

[10]唐孝威（Tang Xiaowei）.风险决策价值函数的数学公式（A mathematical formula of value function for decision under risks）[J].应用心理学（Chinese Journal of Applied Psychology），2010，16（3）：215-217.

[11]胡启洲，陆化普，邓卫（Hu Qizhou，Lu Huapu，Deng Wei）.基于价值函数的城市道路交通安全测度模型（The measuring model of urban road traffic safety based on value function）[J].中国安全科学学报（China Safety Science Journal），2010，20（6）：45-50.

[12]杨燕，文福拴，李力，等（Yang Yan，Wen Fushuan，Li Li，et al）.可用输电容量协调决策的多目标机会约束规划模型与方法（Coordinated model for available transfer capability decision-making employing multi-objective chance constrained programming）[J].电力系统自动化（Automation of Electric Power Systems），2011，35（13）：37-43.

[13]Yang G Y，Dong Z Y，Wong K P.A modified differential evolution algorithm with fitness sharing for power system planning[J].IEEE Transactions on Power Systems，2008，23（2）：514-522.

[14]肖峻，徐兵山，张跃，等（Xiao Jun，Xu Bingshan，Zhang Yue，et al）.一种新的配电网联络线瓶颈分析与改造方法（A new method of bottleneck tie lines analysis and reformation for distribution network）[J].电力系统保护与控制（Power System Protection and Control），2012，40（10）：35-41，47.

[15]葛少云，董静媛，王晓东，等（Ge Shaoyun，Dong Jingyuan，Wang Xiaodong，et al）.基于模糊推理的城市中压配电网供电能力评估（Evaluation of power supply capability in MV distribution networks based on fuzzy reasoning）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2004，16（6）：14-17，71.

Assessment of Load Supply Capability Including Identification of Power Supply Bottleneck

LI Li1，LI Jian-hui1，GAO Chao1，YANG Yan2，GUO Wen-tao2，WEN Fu-shuan3
（1.Guangdong Power Dispatching Center，Guangzhou 510640，China；2.South China University of Technology，Guangzhou 510640，China；3.School of Electrical Engineering，Zhejiang University，Hangzhou 310027，China）

In the assessment of load supply capability，not only the values of the associated criteria have to be calculated，but also the power supply bottlenecks should be identified.The existing approaches cannot systematically and effectively address these issues.Given this background，to implement the objective of assessment of load supply capability，a value function of the load supply margin is defined to guide the reasonable allocations of loads among buses in the system，and to identify the power supply bottlenecks.First，an optimization model for assessing the load supply capability is developed with the maximization of the value function as the objective，and security limitations as constraints.The well-developed differential evolution（DE）algorithm is employed to solve the developed optimization model.The feasibility and the efficiency of the developed model and algorithm are demonstrated by Guangdong actual power system.

power system；power supply capability；identification of power supply bottleneck；value function

TM715

A

1003-8930（2013）03-0043-07

李力（1970—），女，学士，高级工程师，研究方向为电力系统调度运行、电网运行风险分析与控制。Email：lili@gddd. csg.cn

2012-11-12；

2012-12-29

国家高科技研究发展计划（863计划）资助项目（2011AA05A105）；广东电网公司重点科研项目

李剑辉（1963—），男，学士，工程师，研究方向为电力系统调度运行、电网运行风险分析与控制。Email：lijianhui@gddd. csg.cn

高超（1982—），男，硕士，工程师，研究方向为电力系统规划、电网运行风险分析与控制。Email：gaochao@gddd.csg.cn