基于插值优化的GM（1，1）模型在油田年产油量的应用

李小飞

（长江大学工程技术学院，湖北荆州 434020）

年度产油量预测是油田开发年度工作部署的重要环节，做好年度产油量的预测，以利于调整部署和确定油田生产投资的规模与决策方向[1]。在油田产油量预测方法中，常用的方法有趋势预测法、水驱曲线法、递减曲线法和增长曲线法，这些方法对于中长期产量预测以及油田可采储量计算非常有效，但对预测年度产油量的适应性差，预测精度较低。另外还有神经网络及遗传算法等，但是，这些算法的有效性都是建立在训练样本量比较大的基础之上。

灰色系统理论[2]由邓聚龙教授提出，它是把一般系统论、信息论及控制论的观点和方法同数学方法结合起来，发展出的一套解决信息不完全系统的理论和方法，它可以对动态系统做出分析、建模、预测、决策、控制等，已广泛运用于工农业生产[3,4]、社会经济管理[5,6]、科学技术研究[7,8]、公共卫生管理[9,10]、疾病预测监控[11,12]等领域，并取得了巨大成功。GM（1，1）预测模型是以灰色系统理论为基础，通过原始数据的处理和灰色模型的建立,对系统的未来状态作出科学的定量预测的一种方法；目前较为成熟的预测方法已超过200 种，各种不同的预测方法有其所适用的特定对象，不存在一种普遍“最好”的预测方法。之所以采用GM（1，1）模型是基于以下两个方面的考量：第一，目前的预测方法多以数理统计为基础，对样本量有较高的要求；第二，计算量相对较小,普通电脑即可完成计算。但是，对于常规的GM（1，1）模型，由于一些不确定性因素和对预测精度的要求，往往需要对常规模型的参数进行修改，以达到预期效果。

近年来，许多作者提出改进的GM（1，1）模型的思想：文献[13]利用Lagrange 插值公式、文献[14]利用Newton-Cores 公式、文献[15]利用Gauss-Chebyshev 公式重构背景值。本文在结合以上作者的思想基础上，利用新的插值优化思想重构背景值，并以文献[16]中的年产油量数据为例，讨论改进后模型的精度和预测的可行性。

1 GM（1，1）预测模型

设原始数据列为：

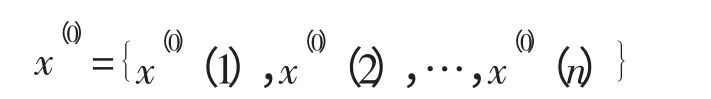
对x（0）进行一次累加生成（1-AGO），以弱化其随机性，强化其规律性，得到累加数据列

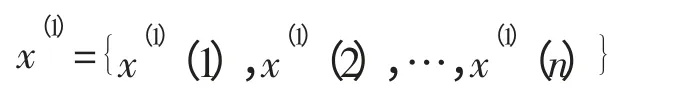
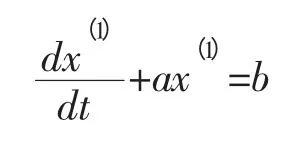
习惯把a，b 分别称为发展系数和灰色作用量。根据最小二乘法可以计算上述参数，做向量参数：

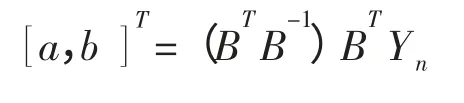
这里：

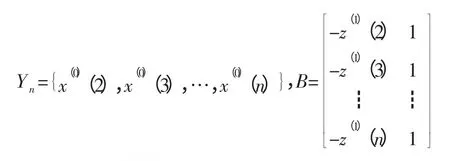
在上式中，z（1）（k+1）称为模型的背景值，且

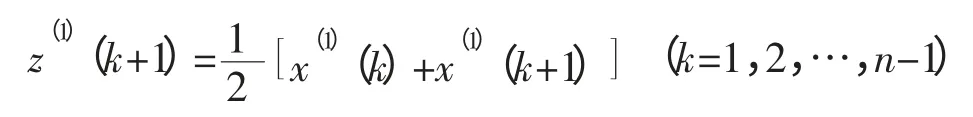
白化形式微分方程的时间响应函数即为预测函数：

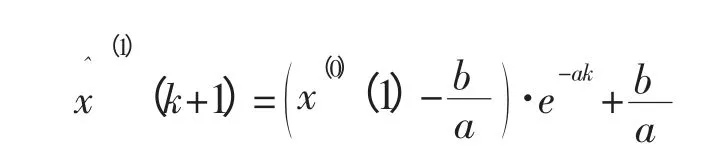
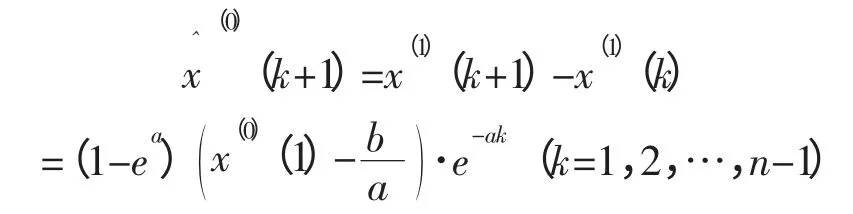
在上述常规GM（1，1）建模过程，可以发现，发展系数和灰色作用量对模型的求解和预测精度有很大的影响。然而，发展系数和灰色作用量又取决于背景值的构建。因此，为了达到预测的高精度，需要优化背景值。

2 基于插值优化的GM（1，1）模型

在上述GM（1，1）模型中，连续使用紧邻均值生成：

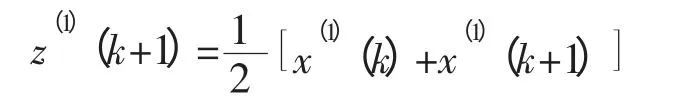
会对发展系数和灰色作用量在求解过程中产生很大的误差，为了克服这个缺陷，给出了一种新的基于插值优化的方法构建背景值，并采用数值逼近思想来解决这一问题，以减少误差。步骤如下：

（1）将区间［k，k+1］等分成三个区间：

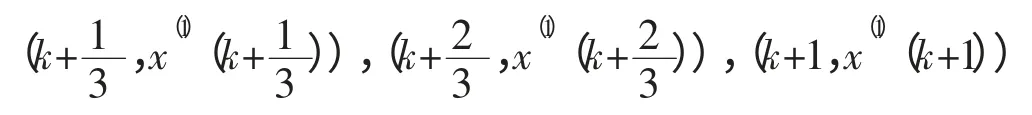
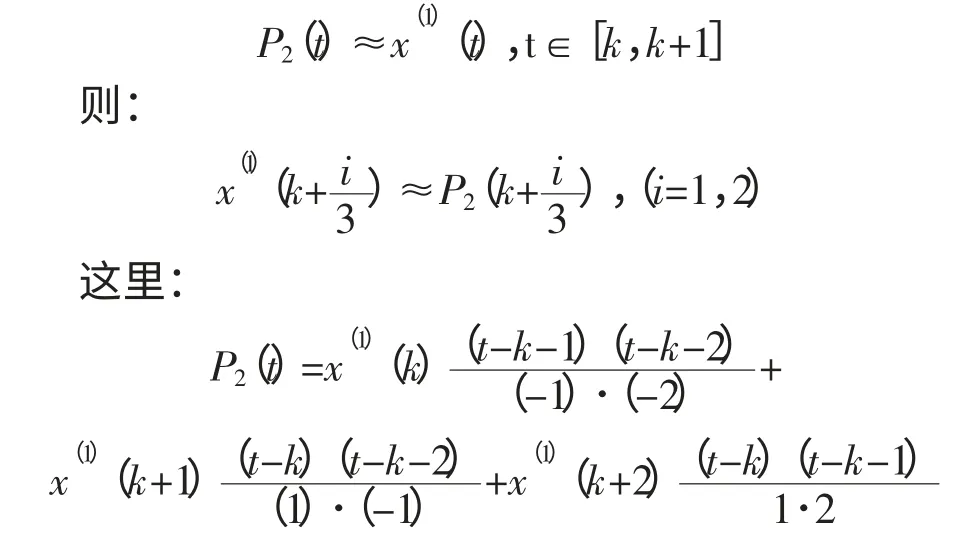
利用数学方法可以得到：

（3）每一个区间内的插值函数为：

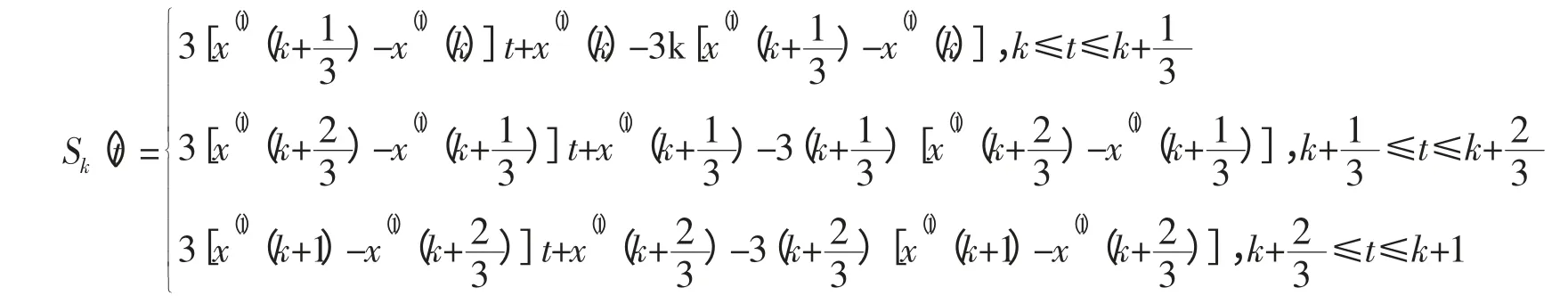
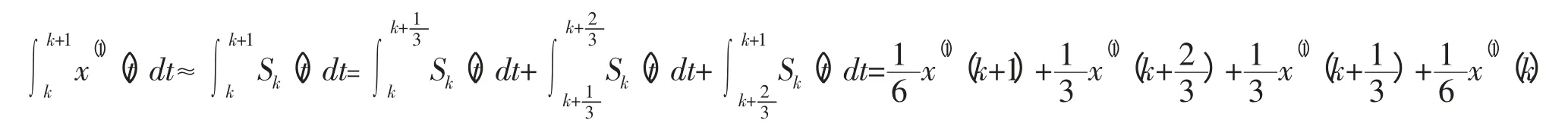
将步骤（2）的结果代入上式，得：

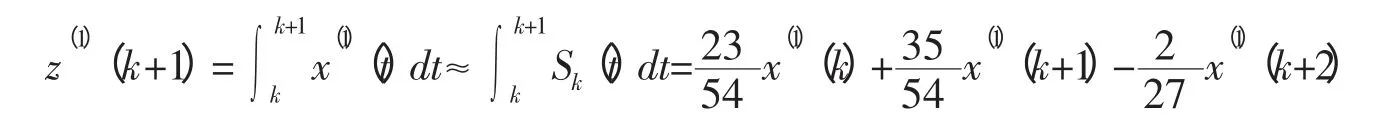
3 预测实例

以文献[16]中某油田1985-1989年的年产油量数据为原始数据列，通过传统的GM（1，1）模型和改进的GM（1，1）模型对1985-1989年的产油量进行预测，比较平均相对误差。

利用传统的GM（1，1）模型和本文的模型进行编程预测1985-1989年的预测值，并分析了产生的相对误差（见表2）。

由表2可以发现，传统的GM（1，1）模型的平均相对误差是3.78%,而改进后的GM（1，1）模型的平均相对误差为2.30%,且预测精度较为提高，模型适用于年产油量的预测。表3为利用改进的GM（1，1）模型预测1990-1994年的年产油量，与实际值对比误差为3.12%。模型可以外推，且具有较好的精度。

4 讨论

GM（1，1）模型的预测精度取决于初始条件的选取和背景值的构造形式，因此在实际生产和生活中，由于初值的不同，对模型的预测有一定的影响。改进后的GM（1，1）模型采用了比较合理的方法来确定GM（1，1）模型的初值，充分发挥了原始数据序列中每一个数据的作用。改进后的GM（1，1）模型比传统GM（1，1）模型的背景值进行了优化，弥补了传统GM（1，1）模型存在的不足。由于事情的发生有很多复杂的内在和外在因素，所以灰色预测模型也会有一些缺陷，它只是理论上对事情的发生做一些简单的预测。在实际生活生产中，可以选取多种模型对事件进行预测，结合多种预测结果进行分析，提取有用的信息，做出有利于决策者的实际决策。

表1 1985-1989年某油田实际年产油量（单位：104t）

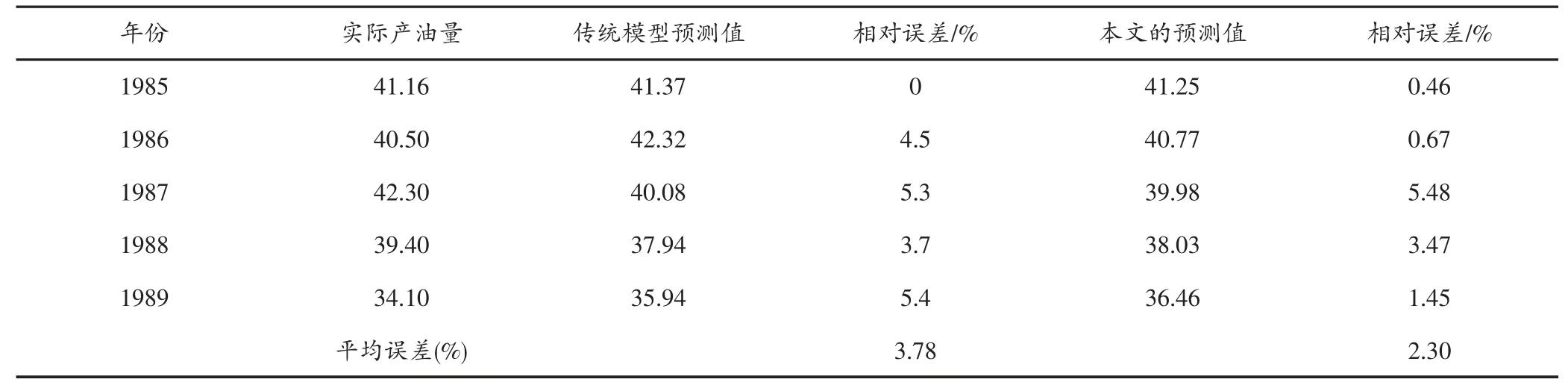
表2 1985-1989年某油田实际年产油量与预测年产油量对比（单位：104t）

表3 1990-1994年某油田年产油量的预测值（单位：104t）

［1］胡建国，任玉林，张维，等.油田老井月度自然产量的预测方法［J］.石油学报，2007，28（3）:109-111.

［2］邓聚龙.灰预测与灰决策［M］.武汉:华中科技大学出版社，2002.

［3］王腾军，赖百炼.基于GM（1，1）数据融合算法的滑坡预测研究［J］.测绘学报，2012，（5）:63-65.

［4］邓琪，王琪，等.GM（1，1）在工业固体废物产生量预测中的应用［J］.环境科学与技术，2012，35（6）:180-183.

［5］李柏洲，罗小芳.基于GM（1，1）三次曲线模型的发明专利对大型企业利润影响研究［J］.软科学，2012，26（6）:6-9.

［6］张云龙，刘茂.灰色GM（1，1）模型在火灾事故预测中的应用［J］.南开大学学报（自然科学版），2009，42（1）:11-15.

［7］刘永阔，谢春丽.基于GM（1，1）模型与灰色马尔可夫GM（1，1）模型的核动力装置趋势预测方法研究［J］.原子能科学技术，2011，45（9）:1075-1079.

［8］佘娣，谢劭峰.稳健动态GM（1，1）模型及其在变形预报中的应用［J］.工程勘察，2012，（9）:51-53.

［9］王琦，郑静.灰色GM（1，1）预测模型在门诊量预测中的应用［J］.中国医院管理，2009，27（2）:26-27.

［10］姚茂钧.灰色系统GM（1，1）模型在医院经济预测中的应用［J］.中国卫生统计，1993，10（3）:25-26.

［11］张旭东，沈思魁.应用灰色预测模型GM（1，1）对四川省血吸虫病人群感染率进行分析及预测［J］.预防医学情报杂志，2012，28（3）:181-183.

［12］张维朋.女性胆固醇随年龄变化灰色GM（1，1）预测模型的建立［J］.科技通报，2011，27（4）:479-483.

［13］Tang Wangmei，Xiang Changhe.The improvement of forcasting method in GM（1，1）model based on quadratic interpolation ［J］.Chinese Journal of Management Science，2006，（6）:109-112.

［14］Li Junfeng，Dai Wenzhan.A new approach of background value-building and its application based on data interpolation and Newton-Cores formula ［J］.Systems Engeering-Theory &Practice，2004，（10）:122-126.

［15］Wang Xiaojia.Forecasting modeling and analysis of power engineering in China based on Gauss-Chebyshev formula［J］.Systems Engineering Procedia，2012，（5）:131-136.

［16］田敏，赵永军，等.优化GM（1，1）模型在产油量预测中的应用［J］.油气地质与采收率，2008，15（4）:88-90.