外径检测设备使用过程中的误差分析

梅军建，闫晓栋，张陈兵

(中国人民解放军96617 部队，四川 泸州 646000)

某外径检测设备主要运用于球面外径测量，检测人员在使用过程中发现该设备存在一定的误差，对检测结果有着重要的影响，直接导致检测数据出现误差，因此对该设备检测过程中的误差分析就显得尤为必要。结合该检测设备的结构特点，建立了误差分析模型，通过微积分计算分析了误差变化规律［1］，给出了影响该设备的误差因素，对全面分析外径检测数据具有重要意义。

1 数学模型

某外径检测设备主要由测量装置、校准装置、基准板、基准座、百分表等组成，结构如图1 所示。

以O1为圆心建立直角坐标系，圆O1表示外径检测设备，圆O2表示校准装置，圆O1和圆O2的圆心距d 表示外径检测设备与校准装置中心之间的偏移量，忽略百分表的误差［2］和校准装置的误差。

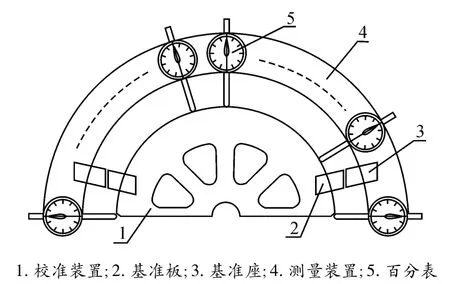
图1 外径检测设备结构示意图

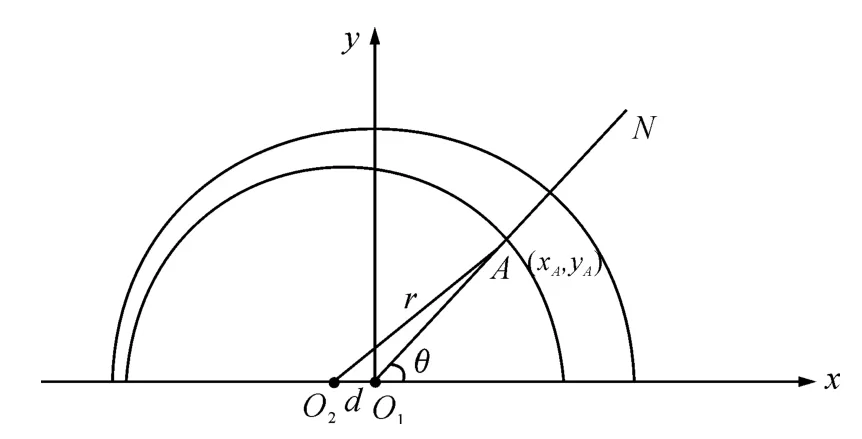
图2 外径检测设备数学模型

角度θ 为某一百分表在外径检测设备上的位置角，半径r 为校准装置标准值，直线O1N 与圆O2的交点A 为百分表与校准装置的接触点，线段O1A 的长度为百分表的实际标定长度值。

设L 为外径检测设备与校准装置中心偏移量的最大值，且根据实际情况可知0 ＜L ＜＜r，则圆O2的解析方程为

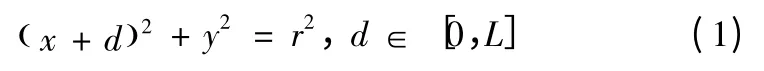
直线O1N 的解析方程为:

联立式(1)、式(2)求得方程组的解即为圆O2与直线O1N 的交点A 的坐标:

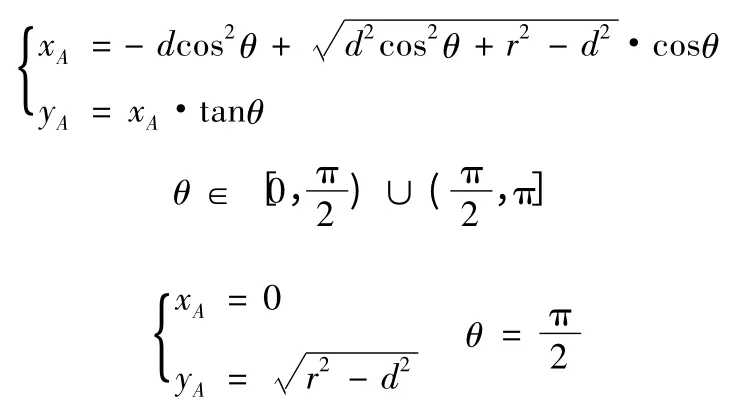
该解即为圆O2与直线O1N 的交点A 的坐标。因此O1A 的长度为

某一角度的误差Δ 为

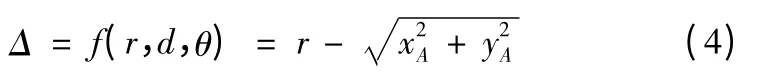
化简得:

算术平均误差为［3］

当n→∞时

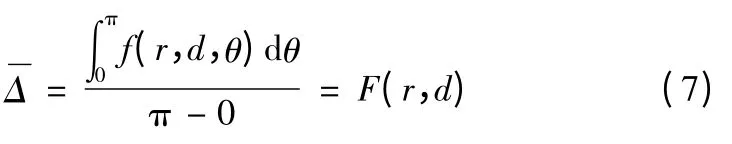
其中r∈［0，+∞)，d∈［0，L］，0 ＜L ＜＜r。

对函数F(r，d)在其定义域内分别求偏导得:

函数F(r，d)在其定义域里，对于变量r 单调递减，对于变量d 单调递增。也就是说误差Δ 随校准装置半径r 的增大而减小，随圆心距d 的增大而增大。

2 算例分析

校准装置圆心与外径检测设备圆心距离d 以及校准装置半径r 分别取不同值时，由式(5)和式(6)计算结果如表1和表2 所示。

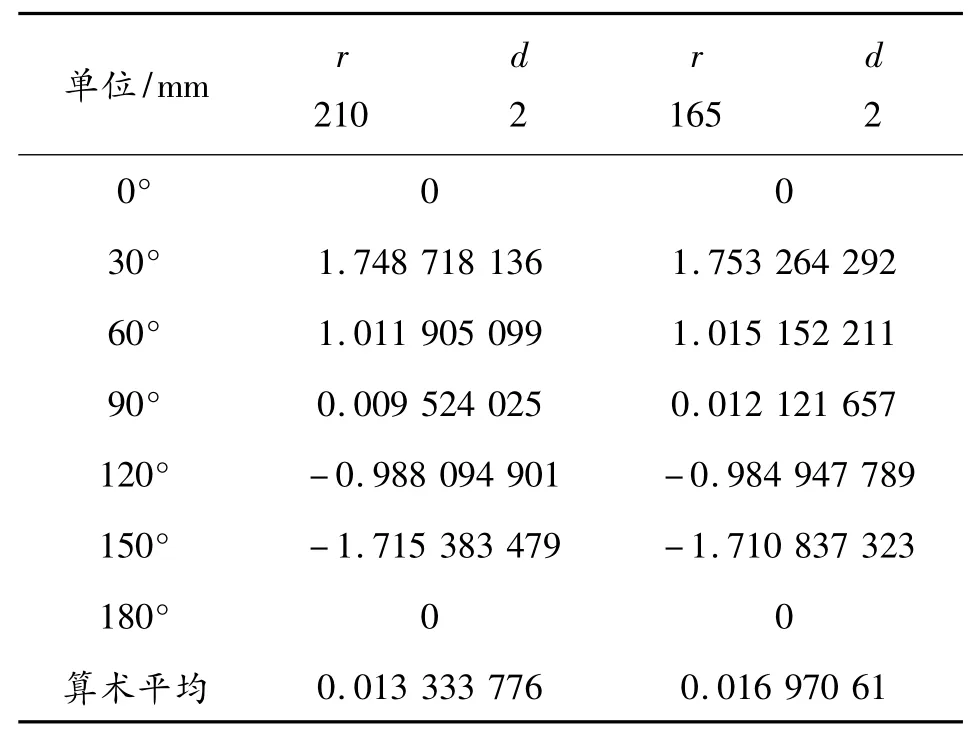
表1 校准装置半径r 对误差结果的影响

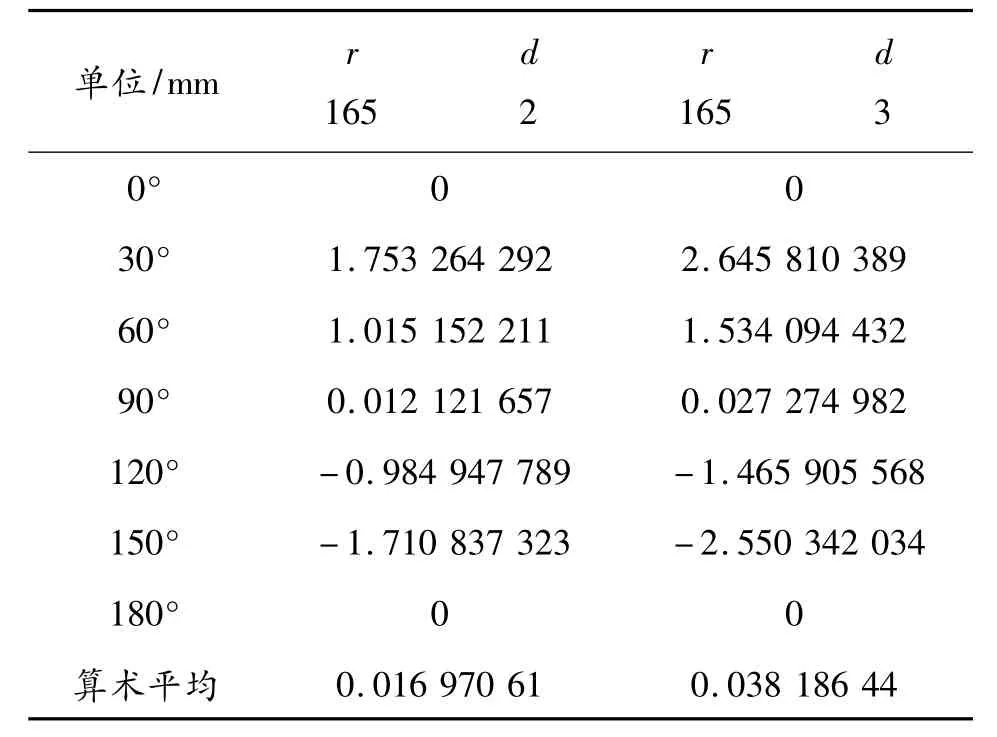
表2 圆心距d 对误差结果的影响

3 结论

使用该设备测量出的半径算术平均误差随校准装置半径r 的增大而减小，随测量装置与校准装置之间的圆心距d的增大而增大。建立数学模型时，忽略了百分表和校准装置存在的误差，仅考虑测量装置本身存在的误差，所得到的误差结果存在一定的局限性，对于这些情况，有待今后进一步研究。

［1］同济大学应用数学系.高等数学［M］.北京:高等教育出版社，2010.

［2］施菊华. 百分表在专用检具中的应用［J］. 计量技术，2002（2）:61-62.

［3］林洪桦.现代测量误差分析及数据处理［J］.计量技术，1997（1）:36-39.