平均声压级的简化算法及其误差修正

武 晨，陆益民，李志远

(合肥工业大学 噪声振动研究所，合肥 230009)

当今噪声污染越来越受到人们的重视，已成为4 大污染之一，各种生产用的机械设备发出的强大噪声污染了环境，严重影响了人们的生活质量，因此必须加以控制，在控制前后均涉及噪声测量，这些都需要标准化的噪声测量方法来鉴定，以便相互比较和研究低噪声产品。针对该问题我国制订了测量机器噪声的国家标准［1］，一些工业部门也制订公布了为各自产品或行业专用的国家标准［2］。按照国家标准［1-3］规定，测量机械或设备的噪声，通常都需要确定机械或设备所辐射的噪声声功率级量值，为控制噪声提供依据。标准中指出计算声功率级需先计算平均声压级，但平均声压级的计算采用能量平均(式(1)中的第一项)，计算过程比较复杂，因此当各测点声压级的波动范围不超过5 dB 时，在机器声功率级测量方法标准［2，3］中规定，建议简单地用各个测点声压级的算术平均(式(1)中的第二项)代替能量平均，但近似计算方法不可避免地会产生误差。

本文用数学理论对此近似计算进行了误差分析，推导出最大误差计算公式，并指出该最大误差不仅和各测点声压级的波动范围有关，还和(各声压级的算数平均/10-最小声压级/10)的值有关，不能仅仅凭借波动范围来决定该算法的适用性;其次对于声压级波动范围在6 ～10 dB 的情况，提出了具体的修正方法，扩展了该近似计算的应用范围。

1 最大误差分析

设机器测量包络面上N 个测点的声压级分别为xi(i =0，1，2，…，N-1)，则平均声压级［4］的精确公式与近似计算公式之间的误差ΔY 为

根据傅里叶级数:

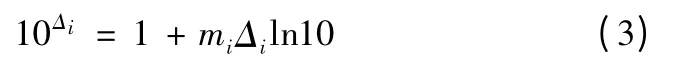
式(3)中:

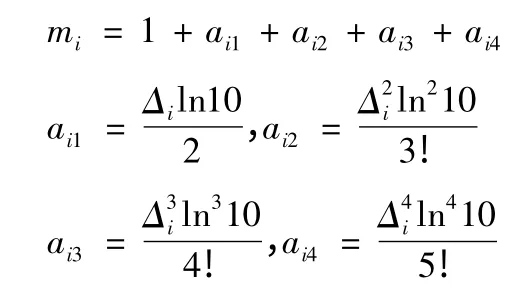
代入式(2)中得

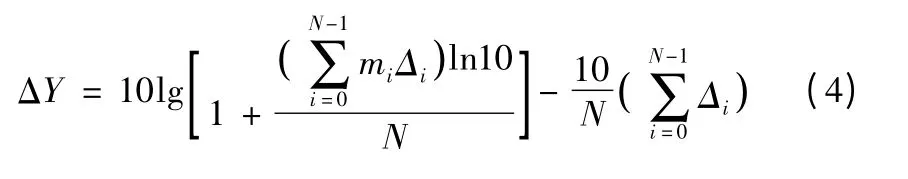
令

式(5)中:

则式(4)可化为

ΔY 为关于M 的增函数，所以要求最大误差，应取:

代入式(7)得:

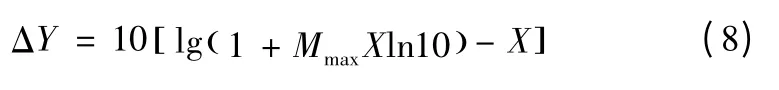
令

计算得:

故最大误差为

根据式(11)，当波动范围为5 dB 时，即b=0.5 dB，最大误差为0.703 dB，当波动范围为6 dB 时，最大误差为1.005 dB，这与文献［2］中规定当波动范围超过5 dB 时，不可用算数平均法来计算平均声压级相吻合。

现根据式(7)画出当波动范围为6 dB(即b =0.6)时的ΔY-X 的曲线，如图1 所示。

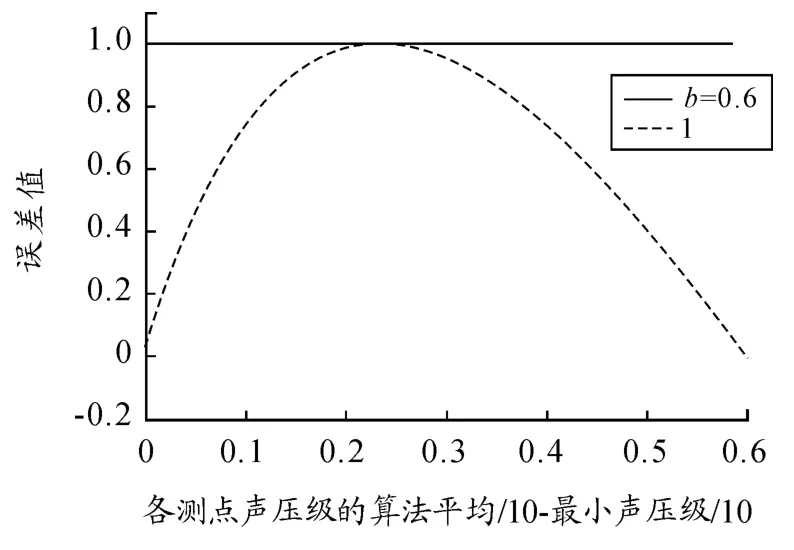
图1 b=0.6 时的最大误差曲线

从图1 中可以明显地看出只有当X 为0.23 时，达到最大误差1.005，其他的大部分情况最大误差都小于1，均可用算数平均来代替能量平均的，因此不能仅凭借波动范围来决定该近似计算方法的适用性。

2 误差修正

根据图1，若对近似计算进行补偿即加上一定的修正值Δ，如式(12):

最大误差曲线将下移Δ，若合理地选择Δ，则可使整个误差曲线在(-1，1)之间，满足最大误差不超过1 的要求。

Δ 的确定方法如下:

当b=0.7 时，根据式(11)计算最大误差为1.341 9，Δ选择0.341 9，这时b=0.7 对应的最大误差曲线在［-1，1］之间。

同理，当b=0.8 时，Δ 选择0.722 4;当b=0.85 时，Δ 选择0.925 7。

当b=0.9 时，最大误差为2.131 6，Δ 选择1.131 6;当X时，b=0.9 对应的最大误差曲线在［-1，1］之间。

当b=1 时，最大误差为2.579 2，Δ 选择1.579 2;当X∈时，b=1 对应最大误差曲线在(-1，1)之间。

综上所述，列出表1。

表1 修正值

当b = 0. 85 ～0. 9 时，Δ 选 择1. 136 7;当X ∈[ 0.01，0.83 ]时，最大误差在(-1，1)之间。

当b = 0. 9 ～1. 0 时，Δ 选 择1. 579 2;当 X ∈[ 0.03，0.77 ]时，最大误差在(-1，1)之间。

根据式(8)、式(12)分别画出修正前，修正后各b 值所对应的最大误差曲线如图2 ～5 所示。

图2 修正前b=0.75 ～1 对应的最大误差曲线

图4 b=0.6 ～0.75 对应的修正后的最大误差曲线

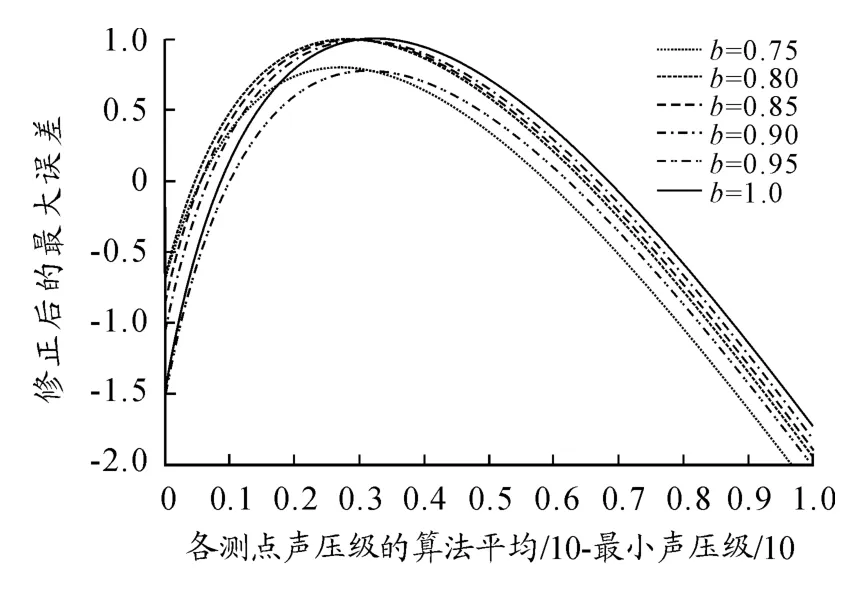
图5 b=0.75 ～1 对应的修正后的最大误差曲线

从图2 ～5 中可以看出，当要求最大误差为1 时，可用范围已扩展了很多。

以上的修正值是当允许的最大误差在1 以内，当要求为其他值时，则不满足要求。针对上述问题，按照如下步骤进行修正。

首先确定b 的值，如果b 值在以上所给的某2 个相邻的b 值之间，选择较大的b 值，这时选定了误差曲线，然后计算X 值(各测点声压级的算数平均/10-最小声压级/10)。如果计算的X 值在图6 横坐标中标出的相邻2 个坐标值之间，则根据图6，修正值Δ 为这2 个相邻横坐标在选定的曲线上所对应的纵坐标中较大的值。

图6 修正前b=0.6 ～1 对应的最大误差曲线

在此给出具体的实例来说明修正方法与步骤:

当计算出X=0.19，波动范围为9.7，即b=0.97，允许误差为0.707 时，从图6 中查出0.19 在0.18 和0.2 之间，根据图6，X=0.2 对应的误差值较大，所以取X =0.2。波动范围9.7 对应的b 值在0.9 和1 之间，选较大值b=1，最后在曲线b=1 上找到X =0.2 对应的误差值为2.4，大于允许误差0.707，所以修正值为Δ=2.4-0.707 =1.693(dB)。

根据式(12)画出b=0.97 时，修正后的最大误差曲线如图7 所示。

图7 修正后b=0.97 所对应的误差曲线

从图7 中找到X =0.19 对应的最大误差在0.4 和0.6之间，满足要求。

3 应用实例

下面是一组实际测得的变压器表面上各个测点的声压级:

(71.5，69.5，69.4，68.2，68.3，72.9，70.7，68.5，68.8，70.0，68.9，69.2，69.3，70.1，70.7，71.3，72.3，73.3，73.5，73.1，72.8，75.0，75.5，77.0，77.2，77.4，76.0，76.0，72.9)

可以看得出b =0.92，X =声压级的算数平均/10-最小声压级/10 =0.39。

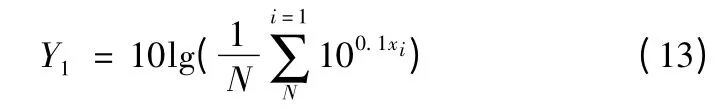
按照式(13)计算得到平均声压级为73.05。

按照式(14)计算得到平均声压级为72.05。

如果规定的允许误差为0.9，那么按照本文所给的修正方法得到修正值Δ 为1.4，修正后的平均声压级为73.45，与式(11)的计算结果相差0.4，小于允许误差1，满足要求，因此可以用算数平均代替能量平均。

4 结束语

本文应用数学理论推导出了使用近似计算方法所引起的最大误差公式，验证了当测量各点声压级波动范围不超过5 dB 时，误差为0.703 dB，可用声压级的算术平均代替能量平均，与文献［5-10］相符合。并提出在决定能否用近似计算时既要考虑波动范围又要考虑(声压级的算数平均/10-最小声压级/10)的值，国标［2，3］中仅凭借当波动范围超过5 dB 就不能用近似计算方法的建议是不合理的，最后对波动范围超过5 dB 的情况加以修正，使得当波动范围不超过10 dB 时均可用算数平均来计算平均声压级，拓展了该近似方法的应用范围。

［1］GB/T 3768—1996，声学-声压法测定声源声功率级-反射面上方采用包络测量表面简易法［S］.

［2］GB/T 1094.10—2003，电力变压器 第10 部分:声级测定［S］.

［3］湖北省标准化协会.机器噪声声功率级测量方法标准译文汇编［Z］.1982.

［4］杜功焕，朱哲民，龚秀芬.声学基础［M］.2 版.南京:南京大学出版社，2001.

［5］钟恭良. 论声压级平均算法［J］. 应用声学，2009，28（3） :174-176.

［6］李中付，谢永安，熊淦. 平均声压级近似计算误差分析［J］.测试技术学报，1996，10（2） :711-714.

［7］熊敏如，陈安朝，罗莎菲.声压级均值计算方法对工业噪声检测结果影响的研究［J］. 中国工业医学杂志，1994，7（5） :299-300.

［8］李中付，华宏星，陈之炎.噪声测试中近似计算误差分析［J］.噪声与振动控制，2001，4（2） :46-48.

［9］钟祥璋.机器噪声声功率级测标准［J］.噪声振动与控制，1988，6（3） :55-57.

［10］熊敏如，陈安朝，罗莎菲.工业噪声检测中声压级均值计算方法对检测结果的影响［J］. 湖南预防医学杂志，1993，5（3） :170-171.