某无人机火箭助推发射段动力学仿真

2013-07-03马大为崔龙飞吴跃飞王新春

兵器装备工程学报 2013年10期

马威，马大为，崔龙飞，吴跃飞，王新春

(南京理工大学机械工程学院，南京 210094)

综观国内外无人机的发展现状，无人机在军事领域的应用日益广泛，正在成为现代高科技战争中不可或缺的武器。其中，无人机箱式发射系统构成部件众多、系统复杂。无人机和发射箱之间、系统各部分之间相互作用、相互制约，系统的刚度、阻尼和质量矩阵都随时间不断地改变。整个系统构成一个复杂的随机非线性时变弹性系统［1-3］。

本文以某箱式无人机的发射段为主要研究对象，采用火箭助推发射方式，以无人机发射起飞阶段的飞行稳定性及安全性为指标，建立无人机发射系统的动力学仿真模型［4］，利用动力学仿真软件ADAMS，对某型无人机发射阶段中的沿滑轨起飞这一阶段进行仿真。根据仿真结果，分析了不同火箭安装角和不同机体发射角下无人机的位移、速度、加速度以及滑块与导轨之间的接触力等参数，并得到较合适的火箭安装角和机体发射角。

1 建模理论基础

ADAMS 是一款多体动力学分析软件，能非常方便地对虚拟机械系统进行动力学分析，也为建立复杂的动力学模型提供了方便［5，6］。

ADAMS 多刚体方程基础，平均动能为

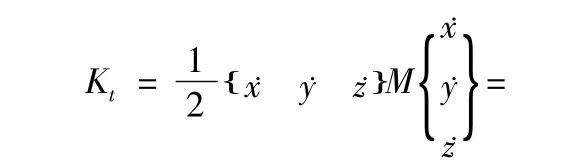
式(1)中:M 为刚体质量;˙r 为刚体质心速度矢量。

转动动能为

式(2)中:ω 为刚体角速度，I 为刚体转动惯量。

总动能为

ADAMS 利用带拉格朗日乘子的第2 类拉格朗日方程导出最大坐标的微分—代数方程。它选取系统内每个刚体质心在惯性参考系中的3 个直角坐标和确定刚体方位的3 个欧拉坐标作为笛卡儿广义坐标，即编制ADAMS 程序。ADAMS 根据机械系统的模型，自动建立拉格朗日运动方程，对每个刚体，列出对应6 个广义坐标带乘子的拉格朗日方程及相应的约束方程为

式(4)中:i=1，2，…，n;j =1，2，…，m;qj为描述系统的广义坐标;Φi为系统的约束方程;Fi为广义坐标方向上的广义力;λi为拉式乘子。

式(4)可写作如下形式:

动能的定义为

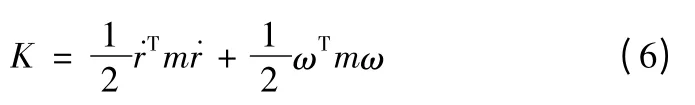
代入式(5)中，合并成简洁的矩阵形式为

对上述代数—微分方程，ADAMS 将二阶微分方程降为一阶微分方程来求解。即ADAMS 将所有拉格朗日方程均写成一阶微分方程形式，并引入，得到:

综上所述，对多刚体系统ADAMS 可列出刚体运动方程，约束代数方程，外力的定义方程，自定义的代数—微分方程等。令为状态向量，则系统方程可写为:

2 无人机仿真模型的建立

2.1 无人机三维实体几何模型的建立

ADAMS 是使用范围最广的机械系统动力学分析软件，其三维实体建模功能较弱，对无人机发射系统的建模很难实现。因此，本文采用SolidWorks 建立无人机的三维实体模型，然后简化模型，经装配检查无误后导入ADAMS 中。

2.2 无人机发射系统各部件间的连接

为计算方便，视车体为大地，发射箱与车体之间为弹性连接，采用弹簧阻尼模拟;导轨与导轨座，导轨座与发射箱体之间分别用固定副锁定。无人机与4 个滑块用固定副固定，此固定约束在滑块滑离导轨后失效。发射箱机尾侧通过旋转副与车体连接;机头侧通过一个弹簧阻尼来模拟箱体与车体间的连接，以等效液压起落装置。滑块与导轨间的运动通过接触进行约束，通过与导轨碰撞受力使飞机沿导轨运动。为简化计算，火箭与飞机的连接在火箭安装位置用固定副表示［7］。

2.3 无人机箱内运动载荷分析

无人机在导轨滑行助推段，飞行速度较低，且受到导轨的约束，因此不考虑空气阻力;燃气流对无人机的发射也有一定影响，由于不是本文研究重点，也不作考虑。无人机此时受到的力主要是:助推火箭的推力、无人机发动机的推力、导轨对机体(滑块)的支撑碰撞约束力、限位开关未开锁时的闭锁力以及重力。

1)助推火箭推力。助推火箭的总推力可表示为［8］

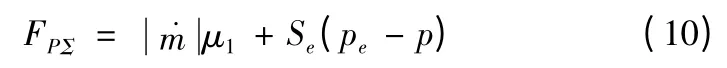
火箭推力的大小一般根据无人机总重(机体重与皮重)，以及无人机发射时所需达到的速度与高度，考虑发射时的动能损失以及外在环境因素(例如风的存在)的影响，并在给定加速度的限制范围内，由动能定理计算得出助推器的设计总冲。然后根据已有的实验数据给出助推火箭的推力曲线。如图1 所示。

2)闭锁力。闭锁力是为了防止无人机在发射前由重力的作用或发射箱摆动引起的滑动或振动。根据推力曲线，可以得到无人机挣脱闭锁的时间大概在0.015 s 处。由于闭锁力的作用就是固定无人机，所以在施加载荷时，可以直接设成锁约束，利用仿真控制文件中的控制语句(SIMULATE/DYNAMIC，END=1.0E-002，STEPS=10;DEACTIVATE/JOINT，ID=10)，设计其在0.01 s 时失效。

在ADAMS 中，确立无人机的全局坐标系，x 轴为无人机的前进方向，y 轴为无人机的上升方向，z 轴为无人机的前进方向的右向，则构建的无人机动力学仿真模型如图2 所示。

图1 火箭推力曲线

图2 ADAMS 中无人机的动力学仿真模型

3 无人机仿真及结果分析

无人机沿导轨发射阶段由于导轨的约束，无人机固有参数和外部参数对机体的运动及姿态影响较小。为简便计算，机体横向发射角取0°，分别以机体纵向发射角和火箭安装参数为变量，在地面坐标系和机体坐标系中，对某型无人机发射阶段运动进行仿真，得到不同条件下无人机飞离导轨瞬间的位移、速度、加速度等初始参数的时间历程曲线以及无人机滑块与导轨之间的接触力等参数的时间历程曲线。

3.1 不同火箭安装角的仿真结果及分析

在机体发射角为0°的前提下，选取火箭安装角分别为0°、2°、5°、8°、12.5°对无人机的发射进行仿真分析，仿真结果如下。

1)无人机的位移曲线。位移曲线如图3 所示。

图3 无人机的位移曲线

2)无人机在Y 方向的速度曲线。速度曲线如图4 所示。可见火箭安装角在5°时，火箭上升推力能够克服自身重力，无人机开始产生上升的速度，因此安装角不能太小。

图4 无人机在Y 方向的速度曲线

3)无人机质心的加速度历程曲线。由图5 得出，火箭安装角为0°和2°时，无人机在导轨滑行阶段有稍微的波动，从8°开始，加速度幅值波动逐渐变大，对导轨损伤变大。因此，无人机的安装角在5°左右时，无人机飞行较平稳。当无人机脱离导轨后，加速度稳定不变。

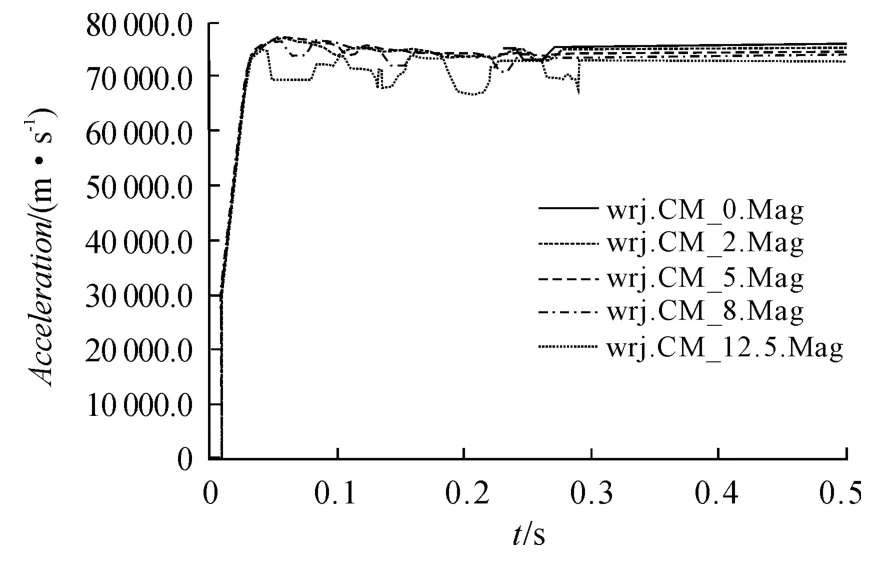
图5 无人机质心的加速度历程曲线

4)无人机前滑块与导轨的接触力曲线。接触力曲线如图6 所示。

图6 无人机前滑块与导轨的接触力曲线

5)无人机后滑块与导轨的接触力曲线。通过分析接触力曲线可知，随着火箭安装角的增大，接触力先变小再增大，显然不能过大，否则对导轨的碰撞比较剧烈，不利于发射;并且可以看出火箭安装角在5°时，接触力最小，碰撞幅度较小，有利于发射(图7)。

图7 无人机后滑块与导轨的接触力曲线

3.2 不同机体发射角的仿真结果及分析

由前面的仿真结果可知火箭安装角为5°时，发射较为平稳，并且能达到速度和高度的要求，因此，取火箭安装角为5°时，对无人机在最初0.5 s 内不同发射角下沿导轨发射进行仿真。

1)不同机体发射角下的合位移曲线。合位移曲线如图8 所示。不同机体发射角下的Y 方向的位移曲线如图9 所示。从位移曲线中可以看出，随着机体发射角的增加，无人机在上升方向的位移不断增加，但合位移却在减少。

图8 无人机的合位移曲线

图9 无人机Y 方向的位移曲线

2)不同机体发射角下的Y 方向的速度曲线。不同机体发射角下的合速度曲线如图10、图11 所示。从速度曲线可以看出，随着机体发射角的增加，无人机在上升方向的速度不断增加，但合速度却在减少。

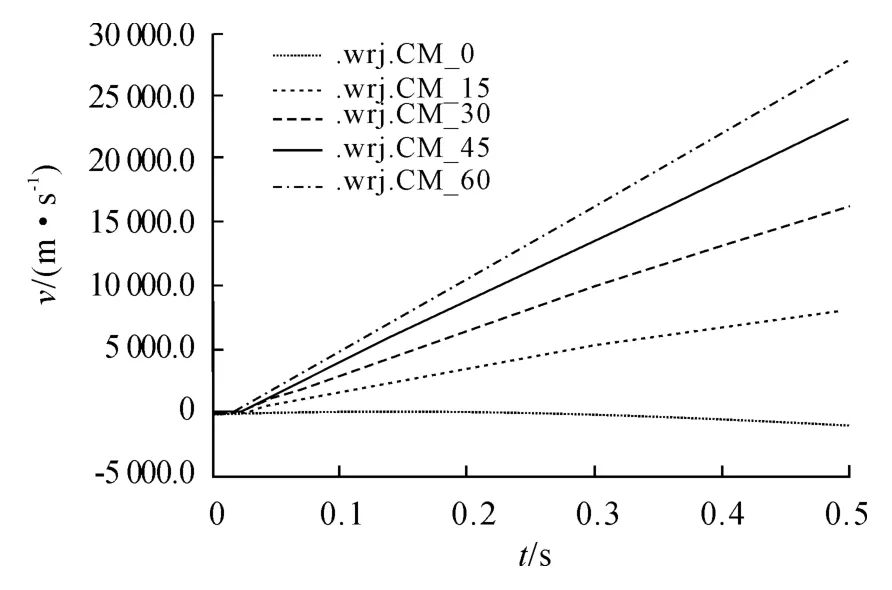
图10 无人机Y 方向的速度曲线

图11 无人机的合速度曲线

3)不同机体发射角下，飞机质心的加速度变化曲线。从图12 中可知:无人机的加速度随着机体发射角的增加而减小，在导轨滑行阶段因有碰撞而产生波动，在0.29 s 左右时，滑块脱离导轨，没有了导轨的阻力和碰撞，加速度的幅值增加一点，并且稳定。

图12 无人机的加速度变化曲线

无人机在发射阶段加速度的大小直接关系到机体材料以及飞机内部各部件仪器的承受程度。加速度的稳定很重要。机体发射角为45°时，加速度幅值波动比较小。

4)不同机体发射角下的前滑块与导轨之间的接触力曲线。不同机体发射角下的后滑块与导轨之间的接触力曲线如图13、图14 所示。在0.01 s 内，由于闭锁力的存在，无人机滑块与导轨间的接触力为0，0.01 s 之后，因火箭安装角的存在，滑块与导轨产生起伏碰撞，接触力起伏变化;机体发射角从0°增加到45°过程中，接触力减小;从45°增加到60°时，接触力又增大。可见，机体发射角在45°左右时，无人机发射比较平稳。