强夯法处理风成砂地基的数值模拟分析

张建辉，杨培轩

（河北大学建筑工程学院，河北保定 071002）

强夯法处理风成砂地基的数值模拟分析

张建辉，杨培轩

（河北大学建筑工程学院，河北保定 071002）

采用ANSYS／LS－DYNA程序建立三维有限元模型，对强夯法处理风成砂地基的过程进行了数值模拟，分析了风成砂地基的沉降、应力、塑性应变时程曲线等的变化特征，对强夯加固风成砂地基的机理进行了探讨.分析表明，所采用数值方法适用于风成砂地基的强夯处理模拟，同时关于强夯加固风成砂地基的机理得到一些结论，可为工程实践参考.

强夯法；风成砂；地基处理；数值模拟

风成砂（也称风积砂）在高原、沙漠地区地表分布十分广泛，是该地区绝大多数工程建设均会涉及的特殊地层.风成砂作为一种特殊土，有颗粒细、级配差、结构松散、无黏性、毛细作用不发达等物理力学特征，目前，对于风成砂地基在承载力、附加应力、地基破坏和沉降变形等问题上尚无系统的理论研究［1］.

强夯法是利用夯锤巨大的夯击能，在地基中产生冲击波和动应力对其进行挤密，以降低地基压缩性并提高强度的一种地基处理方法，常用于处理可液化砂土地基和湿陷性黄土地基等.近年沙漠地区的工程实践证明，强夯法处理风成砂地基，经济实用，效果显著［2］.强夯法的应用始于20世纪70年代，由于加固机理复杂，其设计计算方法一直是经验性或半经验性的，工程中通常由现场试夯确定施工参数，但存在费用高、结果易受外界因素影响的问题.多年来，数值方法已成为研究强夯加固机理的一种重要途径，钱家欢［3］最早应用边界元法研究强夯问题，李本平等［4］利用动力有限元法证明加载－卸载双线性模型比较适应于强夯机理分析，近年，蔡袁强等［5］对强夯加固机理进行了数值分析，周世良等［6］对强夯处理高填方的大变形进行有限元数值模拟，总之，在强夯法的研究与应用方面，通过数值分析已取得许多成果.

因此，结合现场试验，通过合理确定土体的应力应变关系、屈服准则以及力学边界条件，由数值方法来模拟强夯加固地基的全过程，进行参数计算，具有不可替代的优势.

本文应用大变形动力响应分析程序ANSYS／LS－DYNA［7］，基于Lagrange数值方法的显式动力学有限元计算方法，对风成砂地基的强夯过程进行了数值模拟，分析强夯作用下风成砂土地基的沉降位移、应力、塑性应变等的变化特征，旨在探究强夯法加固风成砂土地基的效果以及其机理，为相应地基处理的设计计算提供参考.

1 风成砂地基的数值模型

1.1 工程场地概况和地基处理方案

内蒙古某一大型煤化工工厂的地基处理工程，工程场地为风成砂土地基，根据现场工程地质勘察，主要物理力学参数见表1.

表1 风成砂地基的物理力学参数Tab.1 Physical and mechanical parameters of aeolian sand foundation

根据地基承载力要求，经过比较，决定采用强夯法地基处理方案，强夯能级为3 000kN·m，选取重27t、直径2.4m的圆形夯锤、落锤高度11.1m.

1.2 三维数值模型

本文中建立风成砂地基的数值模型时，基于如下3点假定：风成砂地基土体视为水平层状（均质）地基；因工程场地属于沙漠高原，不考虑地下水的影响；假定夯锤为刚体，在夯击过程中夯锤底部始终保持水平.

将夯锤置于地基表面上，计算区域以夯锤底面中点为中心，取为30m×30m×20m（距中心5～10倍夯锤直径）的长方体.将夯锤与计算区域土体一起进行三维有限元网格划分，单元类型均取为Solid 164，各土层界面为单元界面.由于夯锤底面土体所受的动应力很大，应力集中明显，故将夯锤附近2.4m范围内网格细划，且网格尺寸在水平方向向四周成等比增大，在深度方向按土层界面逐渐增大.各土层物理力学参数根据表1换算成ANSYS／LS－DYNA的参数，夯锤参数见表2.

表2 夯锤材料参数Tab.2 Material parameters of the hammer

三维有限元网格模型及其剖面图如图1、图2所示，其中各土层的单元数依次为16 560，12 144，5 520，5 520，5 520，夯锤单元数192个.

图1 三维有限元网格Fig.1 3－D finite element mesh plot

图2 网格剖面Fig.2 Cross－section of mesh plot

王桂尧［8］，彭建兵等［9］研究表明，Drucker－Prager本构模型较为符合强夯以冲击能量破碎并压实土体的原理，其特点也比较适合于砂土类粒状材料.所以本文选用该模型对强夯的动力响应进行数值模拟.

1.3 荷载的施加及边界条件处理

牛志荣等［10］通过强夯实测表明，在夯锤对地面的冲击过程中，地基中的应力波仅有1个尖锋，可将强夯产生的瞬间荷载简化成三角形荷载，如图3所示，又随土质不同，冲击荷载作用时间范围为0.04～0.20s.由于风成砂土干燥且渗透性好，可以直接连续夯击，因此，计算中取强夯冲击荷载作用时间0.085s，间歇时间取3s.根据锤土接触面最大应力pmax计算公式［11］，得本文强夯方案的pmax为2.2MPa，从而得锤土最大接触压力为104kN.因此，夯击过程中，夯锤对地基土体施加的动力荷载（104N）与时间（s）曲线，如图4所示（由于模型中z轴沿深度方向为负，故荷载为负值）.

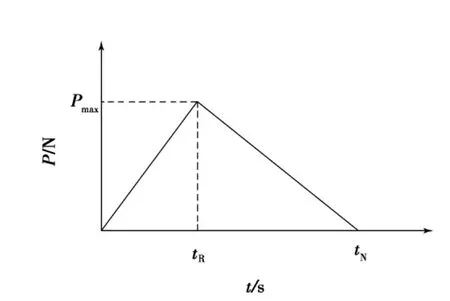
图3 强夯瞬态荷载模型Fig.3 Instantaneous model of compaction load

图4 强夯荷载时间历程Fig.4 Load history of dynamic compaction

根据现场的实际情况，计算区域的边界条件确定如下：在其侧面施加法向约束（侧面分别与x，y轴垂直，即分别施加x，y向约束），在底面（与z轴垂直）施加3个方向的约束；为避免波的反射对土体造成的破坏，边界采用无反射边界；在锤与土体之间定义面对面的侵蚀接触，并采用全瞬态分析；因重点考察土体在冲击荷载作用下的性状，忽略土体自重作用下的固结变形和应力.

2 数值模拟结果及分析

2.1 沉降时程曲线分析

强夯过程中，夯坑中轴线上不同深度处各点A（0），B（2.09m），C（4.1m），D（6.14m），E（8.04m），F（10.24m）的沉降（m）随时间（s）变化的曲线，如图5所示.可看到，在每一次夯击过程中，沉降随着荷载增长，荷载卸去后，土体发生一定的回弹，但并不像弹性材料那样完全回弹，因此，风成砂地基表现出弹塑性材料的卸载后塑性变形累积的性状；另外，土体沉降表面最大，随着深度的增加土体沉降逐渐减小.

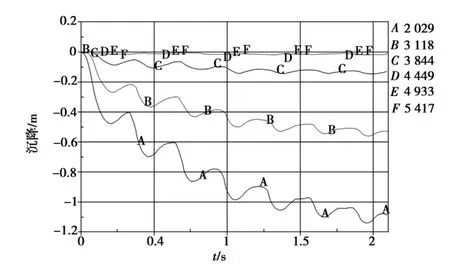
图5 沉降时程曲线Fig.5 Settlement time－history curve

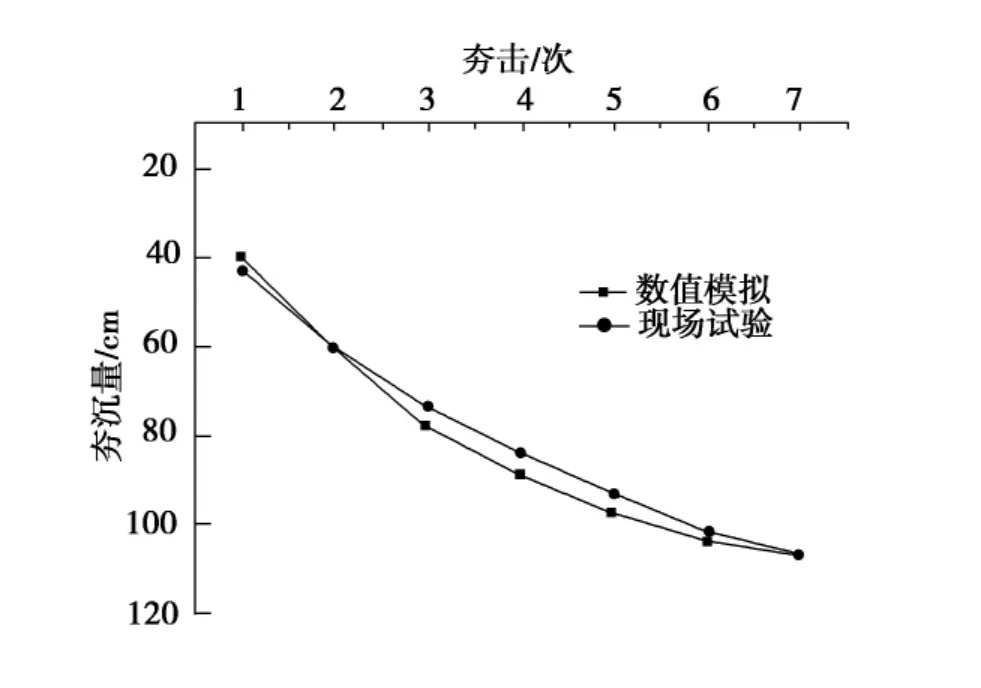
图6 夯沉量随夯击次数的变化Fig.6 Settlement change with compacting number

2.2 沉降分析

夯坑中心沉降（即夯沉量）随夯击次数的变化，如图6所示，图中也给出了工程现场所做的土层沉降试验结果.可以看出，数值模拟与现场测试结果基本一致，夯沉量随夯击次数呈非线性关系增加，但增加幅度逐渐减小.夯击能3 000kN·m时，最大夯沉量11cm左右.按照JGJ79-2002《建筑地基处理技术规范》关于收锤夯击次数（最后2击夯沉量平均值为5cm）的规定，根据计算结果，可确定夯击7次即可收锤.

夯击完成后，夯锤中轴线上及距中轴线1，1.2，1.5，2m的竖直线上各点的沉降沿深度方向的变化情况，如图7所示，图中也给出中轴线各点的现场沉降测试数据，与模拟结果基本一致.可以看到，随着深度的增加，土体沉降均急剧减小；在9m深度处，与中轴线距离不同的各点，沉降基本为零，由此可得到强夯的影响深度约为9m；离夯坑中轴线越近，沉降越大，在距中心轴线2m的土体表面处沉降出现负值，表明该处出现隆起现象.根据有效加固深度和影响深度比值的有关研究结果（0.4～0.7）［12］，以及现场的沉降测试情况，可以得到夯击能3 000kN·m时该风成砂地基的强夯有效加固深度值为6m左右.

不同深度0，0.97，2.09，3m水平面上的土体沉降在水平方向的变化情况，如图8所示.

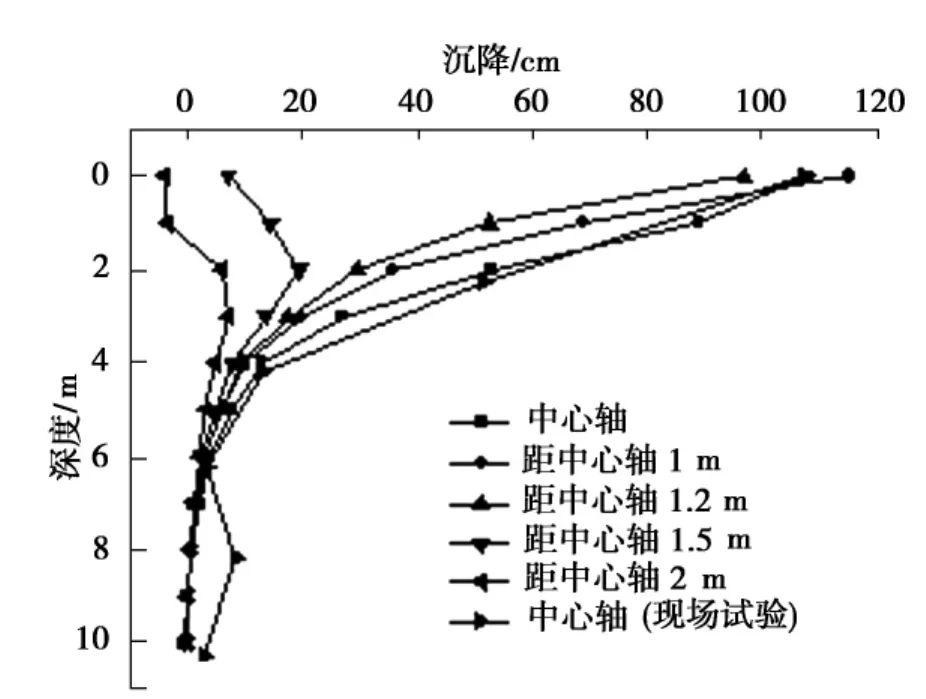
图7 沉降沿深度方向的变化Fig.7 Settlement change in the depth direction

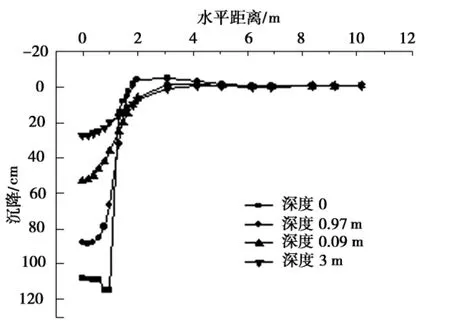
图8 沉降沿水平方向的变化Fig.8 Settlement change in the horizontal direction

可以看出，沉降随着与中心轴的水平距离的增加迅速衰减，而且离地面越近衰减的越快，深度越大处衰减的越慢，曲线越平缓.沿水平方向、距夯坑中心1.7m处，沉降基本衰减至零，距夯坑中心5m处，4条曲线重合，夯击对土层已基本无影响.

2.3 应力与塑性应变时程曲线分析

夯坑中轴线上距地面不同深度处单元A（0），B（2m），C（4m），D（6m），E（8m），F（10m）的最大主应力（Pa）随时间（s）的变化曲线，如图9所示.比较图4可知，夯击过程中最大主应力的变化与强夯冲击荷载的变化基本同步，在每次夯击后基本减少至零.

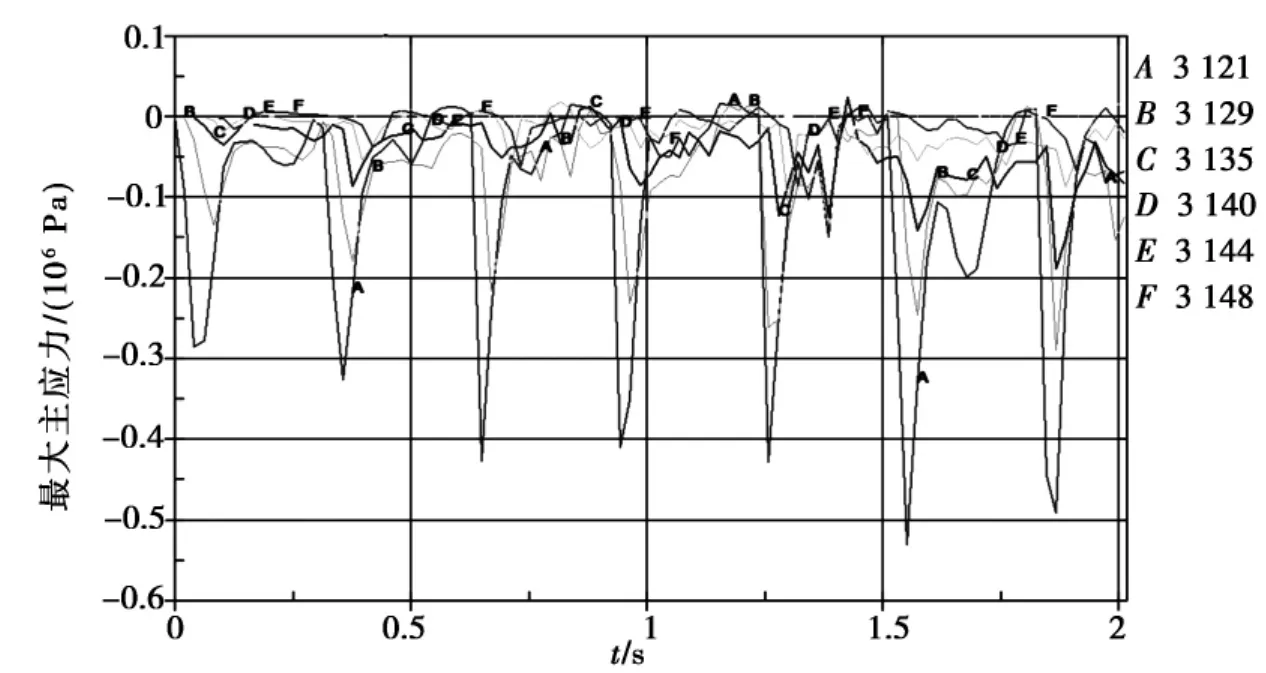
图9 不同深度处最大主应力时程曲线Fig.9 Maximum principal stress history curve in different depth

由图9可看到，夯击过程中，各深度处最大主应力随夯击次数（时间）具有逐渐增加的趋势，说明地基土的强度逐渐增加；土体表面处的最大主应力值最大，随着深度的增加，较快地衰减，至8～10m深度处，已基本衰减至0，说明强夯的影响深度不大于10m.

在2m深度处的水平面上，与夯坑中轴线不同距离单元A（0），B（1m），C（1.2m），D（1.5m），E（2m）的最大主应力（Pa）随时间（s）的变化曲线，如图10所示.可以看到，在2m深度处水平面上，最大主应力随夯击次数（时间）具有逐渐增加的趋势；随着与夯坑中轴线距离的增加而逐渐衰减，自2m以外接近0.

图10 2m深度水平面上最大主应力时程曲线Fig.10 Maximum principal stress history curve on the plane of 2m

夯坑中轴线上不同深度处单元A（0m），B（2m），C（4m），D（6m），E（8m），F（10m）的有效塑性应变随时间（s）的变化曲线，如图11所示.由图11可看到，塑性应变随夯击次数（时间）逐渐增加，而随着深度的增加逐渐衰减，说明夯击过程中，一定范围的土层逐渐产生塑性压缩而密实.可以看出，至8～10m深度处，塑性应变已基本衰减至0，说明了强夯的影响深度，与前述分析一致.

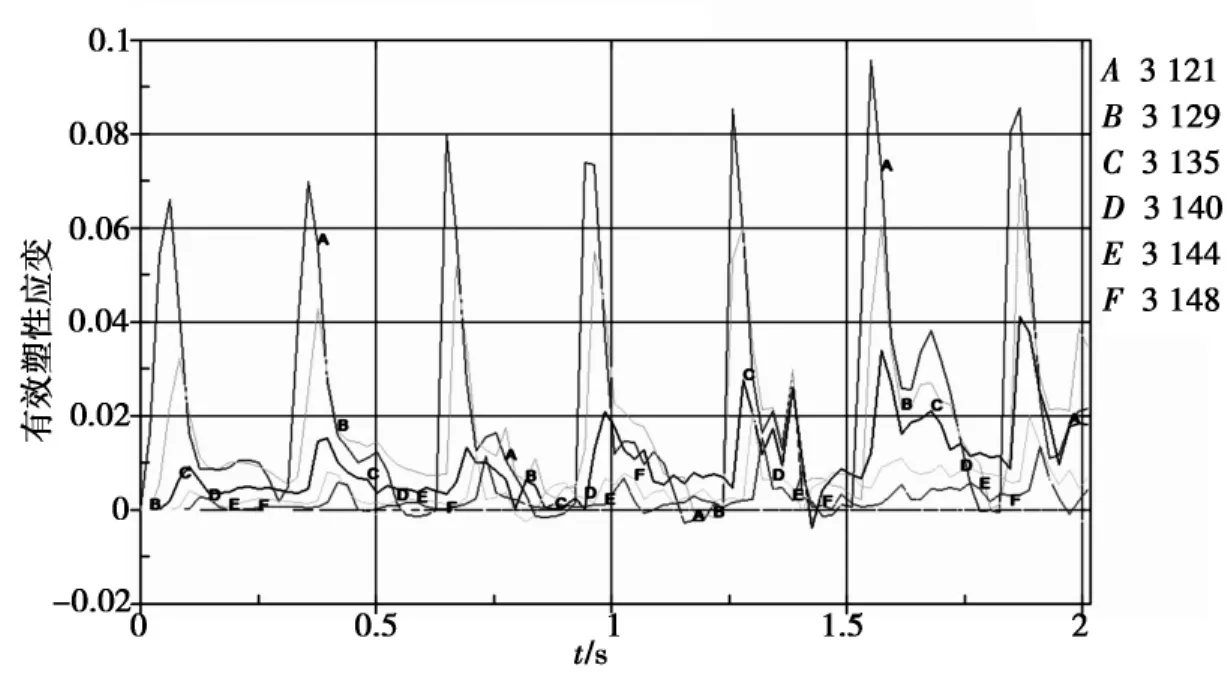
图11 不同深度处塑性应变时程曲线Fig.11 Plastic strain history curve in different depth

3 结 论

上述分析表明，采用弹塑性大变形动力有限元方法（ANSYS／LS－DYNA程序）模拟风成砂分层地基的强夯处理过程，所建立的数值模型合理可行.另外，本文对数值模拟的沉降、最大主应力和塑性应变时程曲线等结果的分析，在一定程度上揭示了强夯加固风成砂地基的机理.对于该风成砂地基的强夯加固处理（夯击能3 000kN·m），得到如下结论：

1）夯沉量随夯击次数呈非线性关系增加，最大夯沉量11cm左右，夯击7次即可收锤.

2）夯击过程中，沉降随着荷载增长，荷载卸去后，土体发生一定的回弹，但并不完全回弹，表现出弹塑性材料卸载后的塑性变形累积的性状.

3）夯击完成后，土体表面沉降最大，随着深度增加沉降均急剧减小；强夯影响深度约9m，有效加固深度约为6m；随着与夯坑中轴线水平距离的增加，沉降也迅速衰减，强夯在水平方向影响距离约为5m.

4）土中最大主应力随着夯击过程有增大趋势，说明土体强度逐渐增加；随着深度的增加较快衰减，至8～10m深度处已衰减至0.

5）土中塑性应变随夯击次数（时间）逐渐增加，而随着深度的增加逐渐衰减，说明夯击过程中，一定深度内的地基土层产生塑性压缩而密实，在8～10m深度处，塑性应变已基本衰减至0，说明强夯影响深度为9m左右，与沉降、应力分析结果一致.

［1］ 刘端锋.风成砂工程性能探讨［J］.西部探矿工程，2004（9）：31－33.

LIU Duanfeng.Discuss about aeolian sand engineering properties［J］.West－China Exploretion Engneering，2004（9）：31－33.

［2］ 王进.高夯击能强夯加固砂土地基的效果分析［J］.中国矿业，2005，14（11）：82－85.

WANG Jin.Impact analysis of sand ground reinforcement using high energy level dynamic compaction［J］.China Mining Magazine，2005，14（11）：82－85.

［3］ 钱家欢，帅方生.边界元法在地基强夯加固中的应用［J］.中国科学：A辑，1987，29（3）：329－336.

QIAN Jiahuan，SHUAI Fangsheng.Application of the boundary element method in the dynamic compacion of soils［J］.China Science：Volume A，1987，29（3）：329－336.

［4］ 李本平.有限元法分析强夯加固机理［D］.杭州：浙江大学，1993.

LI Benping.Finite element method analysis of the mechanism of dynamic compaction［D］.Hangzhou：Zhejiang University，1993.

［5］ 蔡袁强，陈仁伟，徐长节.强夯加固机理的大变形数值分析［J］.浙江大学学报：工学版，2005，39（1）：65－69.

CAI Yuanqiang，CHEN Renwei，XU Changjie.Numerical analysis of dynamic compaction using large deformation theory［J］.Journal of Zhejiang University：Engineering Science，2005，39（1）：65－69.

［6］ 周世良，王多垠，吴友仁.强夯处理高填方的大变形有限元数值模拟［J］.应用力学学报，2008，25（1）：89－93.

ZHOU Shiliang，WANG Duoyin，WU Youren.Nunmerical simulation for stepped reinforced soil retaining wall［J］.Chinese Journal of Applied Mechanics，2008，25（1）：89－93.

［7］ 李裕春，时党勇，赵远.S11.0／LS－DYNA基础理论与工程实践［M］.北京：中国水利水电出版社，2008.

［8］ 王桂尧，胡振南，匡希龙.红砂岩路基强夯处理大变形数值模拟方法与效果分析［J］.岩土力学，2008，29（9）：2451－2456.

WANG Guiyao，HU Zhennan，KUANG Xilong.Large－strain numerical simulation and experimental result reseach about improving red－sandstone embankment by dynamic compaction［J］.Rock and Soil Mechanics，2008，29（9）：2451－2456.

［9］ 彭建兵，陈立伟，邓亚虹，等.车辆动荷载作用下黄土暗穴对路基稳定性影响的数值分析［J］.中国公路学报，2006，19（4）：17－22.

PENG Jianbing，CHEN Liwei，DENG Yahong，et al.Numerical analysis of subgrade stability influenced by hidden holes in loess under dynamic load of vehicles［J］.China Journal of Highway and Transport，2006，19（4）：17－22.

［10］ 牛志荣，杨桂通.冲击荷载下土体位移特征研究［J］.岩土力学，2005，126（11）：1743－1748

NIU Zhirong，YANG Guitong.Studies on the displacement of soils subjected to the impact loading［J］.Rock and Soil Mechanics，2005，126（1）：1743－1748.

［11］ 郭见扬.强夯夯锤的冲击力问题：强夯加固机理探讨之一［J］.土工基础，1996，10（2）：35－39.

GUO Jianyang.Impact force of dynamic hammer（one of discusses about mechanism of dynamic compaction［J］.Soil Engineering and Foundation，1996，10（2）：35－39.

［12］ 徐至钧，张亦农.强夯和强夯置换法加固地基［M］.北京：机械工业出版社，2004.

（责任编辑：王兰英）

Numerical simulation analysis of treating aeolian sand foundation using dynamic consolidation method

ZHANG Jianhui，YANG Peixuan
（College of Civil Engineering and Architecture，Hebei University，Baoding 071002，China）

The Ansys LS－DYNA program was used to establish the 3Dfinite element model and the numerical simulation of the aeolian sand foundation treatment by dynamic compaction was conducted.The settlement，stress and plastic strain time－history curve of the foundation were obtained and analyzed，and the improvement mechanism was investigated.The analysis showed that the method was fit for the simulation of the aeolian sand foundation treatment by dynamic compaction.The results on the improvement mechanism were obtained，and could become a reference for engineering practice.

dynamic consolidation；aeolian sand；foundation treatment；numerical simulation

O178

A

1000－1565（2013）02－0127－07

10.3969／j.issn.1000－1565.2013.02.004

2012－05－04

河北省自然科学基金资助项目（E2011201057）

张建辉（1963－），男，河北辛集人，河北大学教授，主要从事工程力学、地基与基础相互作用研究.E－mail：hbuzjh＠hbu.edu.cn