相空间重构的极端学习机短期风速预测模型

武峰雨，乐秀璠，南东亮

（河海大学能源与电气学院，南京 210098）

开发与利用新能源是21世纪的重要能源战略。风力发电因具有环保可再生、全球可行、成本低且规模效益显著等优点，已经受到了广泛的重视，并成为发展最快的新型能源[1]。由于风速受许多因素影响，具有很大的持续波动性，因此对风速的准确预测变得至关重要[2]。

风速被认为是最能准确预测的气象参数之一。目前关于风速预测的方法有很多，时间序列预测法是应用较多的一种方法。该方法中的因变量和自变量均可以是随机变量，且风速是一个随机性的序列，因此可设定因变量为待预测风速，自变量为风速自身的历史值[3，4]。与神经网络等方法相比，该方法更适用于短期风速预测，但由于模型的阶数不好确定，所以受气候变化影响较大。人工神经网络是用于风速预测较早的机器算法之一，使用非常广泛。该方法具有并行处理、分布式存储与容错性等特征，具有自学习、自组织和自适应能力，可以实现联想记忆、分类与识别等功能，对于求解复杂问题十分有效，文献[5，6]分别采用BP神经网络和径向基神经网络进行风速预测，但其算法容易陷入局部最小问题而得不到最优解，算法收敛慢。文献[7，8]将最小二乘支持向量机应用到风速预测中，较之神经网络，该方法具有更高的精度和更强的鲁棒性。空间相关性法的发展还不是很成熟，与上述方法不同，它需要考虑所预测地点以及与之相近几个地点的风速序列，运用几个地点风速之间的空间相关性进行预测。然而该方法需要很大的数据量，输入信息丰富，可能会在一定程度上提高预测精度[9]。

通过Lyapunov指数可以证明风速时间序列具有混沌特性，而混沌序列短期是可以预测的。因此，利用相空间重构理论可以还原风速时间序列的非线性动力特性，然后利用一定的预测模型可以进行短期风速预测。本文利用相空间重构获得一组最佳的嵌入维数和延迟时间，最后利用极端学习机对重构后的样本进行建模预测，对某风电场的风速时间序列进行短期预测。实例表明，该方法的预测速度快，泛化性能好。

1 相空间重构理论

1.1 概述

Takens定理认为系统中任一分量的演化均由与之相互作用的其他分量所决定。因此，这些分量的信息隐含在任一分量的发展过程中，重构系统相空间只需考察一个分量，通过某些固定的延时点上的观测值重构出原系统，重构空间与原动力系统拓扑等价[10-12]。

对于实际测得一组时间序列

如果嵌入维数和时间延迟为m和τ，则相空间中的相点个数为

重构后构造出的相空间向量Xi（i=1，2，…，N）为

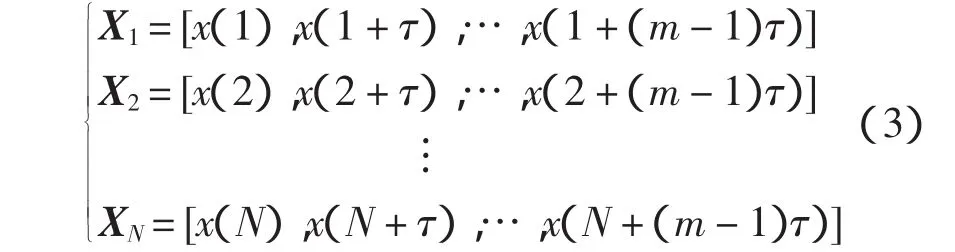
相空间重构是混沌预测的关键，而重构相空间的关键是嵌入维数m和延迟时间τ的选取。

1.2 相空间重构参数的同步计算法

相空间重构参数的同步计算法能够同时估计出延迟时间τ和嵌入窗宽τw，根据

可以求出嵌入维数m。

将时间序列{X（i）}（i=1，2，…，N），分成t个不相交的时间序列，长度为int（N/t），int为取整函数。计算每个子序列的统计量 S（m，N，r，τ）和差量 ΔS（m，N，t），具体过程及符号含义详见文献[11]。随后，得方程

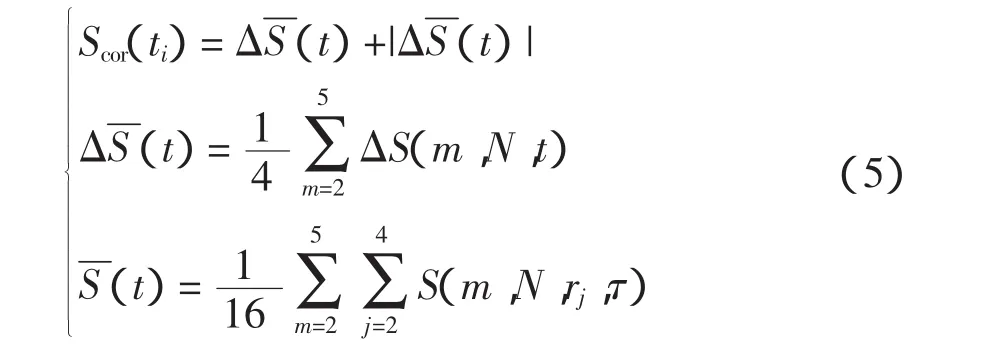
2 极端学习机原理

单隐含层前馈神经网络以其良好的学习能力在许多领域中得到广泛应用，然而传统的学习算法（如BP算法）固有的一些缺陷，成为制约其发展的主要问题。传统的网络大多采用梯度下降法，该方法有以下缺点：①训练速度慢。因为其计算过程需要多次迭代来修正权值和阀值，因此时间长。②容易陷入局部极小值，无法达到全局最优。③学习率选择敏感。学习率对神经网络性能影响较大，若学习率太小，则收敛速度慢，消耗时间长，若学习率太大，则训练过程可能不收敛。探索一种速度快、具有良好泛化能力、获得全局最优解的算法时近年来研究的热点。Huang等[13]提出了极端学习算法，该算法随机产生输入层与隐含层间的连接权值及隐含层神经元的阈值，而且在训练过程中无霜调整，放弃梯度下降法的迭代调整策略，只需要设置隐含层的个数，便可以获得唯一的全局最优解。极端学习机极大地提高了网络学习速度和泛化能力。

给定Q个不同样本的集合，

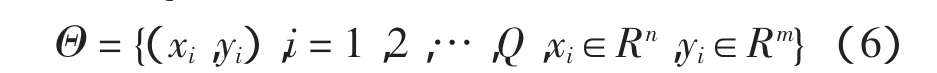
则具有L个隐含层神经元的ELM网络输出[14-16]为

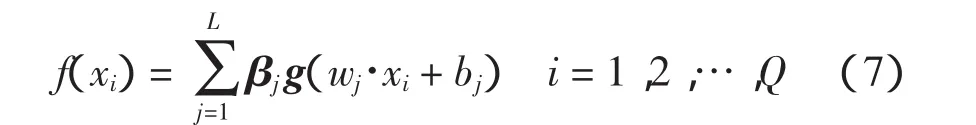
式中：wj=[w1j，w2j，…，为输入节点与第 j个隐含层神经元之间的连接权值向量；bj为第j个隐含层神经元的阈值；βj=[βj1，βj2，…，为第 j个隐含层神经元与输出节点之间的连接权值向量；g（x）为隐含层神经元激活函数。

式（7）可用一个含个方程的线性方程组表示为

式中：H为神经网络隐含层输出矩阵，具体形式为

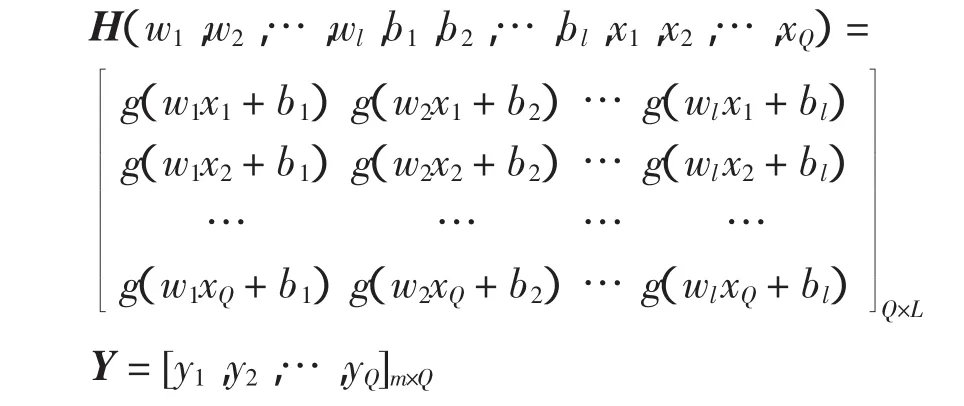
若隐含层神经元个数与训练集样本个数相等，则对于任意的w和b，单隐含层前馈神经网络都可以零误差逼近训练样本。然而，当训练集样本个数Q较大时，则隐含层神经元个数通常取比Q小的数。

当激活函数g（x）无限可微时，单隐含层前馈神经网络参数不需要全部进行调整，w和b在训练前可以随机选择，而且在训练中保持不变。隐含层与输出层连接权值β可以通过解方程组的最小二乘解获得

其解为

式中，H+为隐含层输出矩阵H的Moore-Penrose广义逆。

ELM学习算法主要有以下几个步骤：

（1）确定隐含层神经元个数，设置隐含层阀值b和输入层与隐含层间的连接权值w。

（2）选择隐含层神经元的激活函数，进而计算隐含层输出矩阵H。

（3）计算输出层权值

因此，相比于传统方法，ELM训练过程不需要调整w和b，只需要计算调整β值，这样参数选择过程更加容易，同时可以获得全局最优解，训练速度显著提高。

3 基于相空间重构的ELM风速预测模型

3.1 模型输入输出变量的选择

风速数据是一组随时间变化的序列，记为{xt|t=1，2，…，n}需要利用 Takens理论[17]进行相空间重构，将一维时间序列转化成矩阵形式，以获得数据的关联信息。相空间重构中嵌入维数m和延迟时间τ的大小选取很重要，本文采用上述同步计算法求取嵌入维数和延迟时间。对原数据序列进行相空间重构，构造样本对{Xt，Yt}，其中 Xt={xt-m，xt-m+1，…，xt-1}，Yt=xt，xi为第 i个风速值，m 为输入向量维数。

3.2 样本数据的预处理

数据预处理[18]可以加快模型的训练速度和收敛速度，提高预测精度，因此预测之前需要对原始数据进行处理。样本数据处理的方法很多，本文采用归一化方法，即

3.3 ELM模型参数的选取

ELM预测模型的主要参数是隐含层神经元的数目，它与输入层和输出层神经元的数目有关。据现在的资料表明，对于隐含层神经元数目的确定还没有一个好的方法。极限学习机算法快捷方便，本文研究时，将隐含层神经元初始设为10，再根据训练网络的误差来适当增加，寻找合适的隐含层节点数。误差大于允许范围的增加隐含层节点数，反之，则减少节点数。激活函数选择Sigmoid函数为

3.4 ELM预测模型的评价标准

ELM预测模型的预测效果采用均方误差和平均绝对百分比误差（eMAPE）和来评价，其表达式为

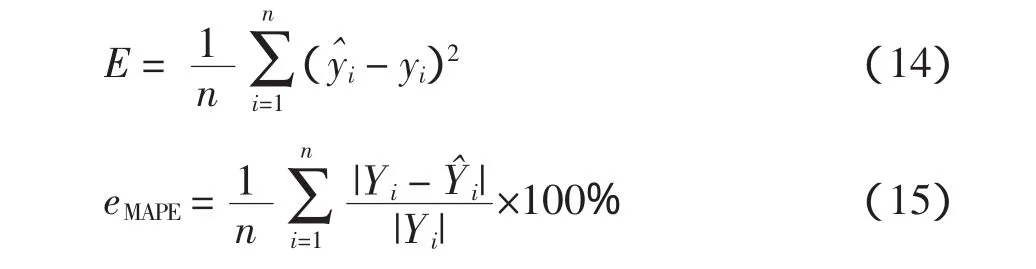
式中，Yi、分别为第i个实际风速值与预测风速值。

4 算例分析

为了验证模型的预测能力，本文利用Matlab编制基于ELM的短期风速预测程序，并进行算例仿真和分析，计算流程如图1所示。

本文采用某风电场前7天的384个实测风速值作为训练样本，数据采样间隔为15 min，建立ELM风速预测模型，对第8天的96个风速值做提前1点（即15 min）的预测。建立模型前对数据进行预处理，选取合理的参数。通过Wolf法估计了最大Lyapunov指数，求得的最大Lyapunov指数为0.239 2，大于0，因此数据具有混沌特性。ELM风速预测模型的输入输出数据采用相空间重构法获得，本文嵌入窗宽为12，延迟时间为2，嵌入维数取7。初始隐含层节点设为10，并且逐渐增加，每个隐含层节点实验20次，查看不同隐含层数的预测效果，仿真结果见表1。

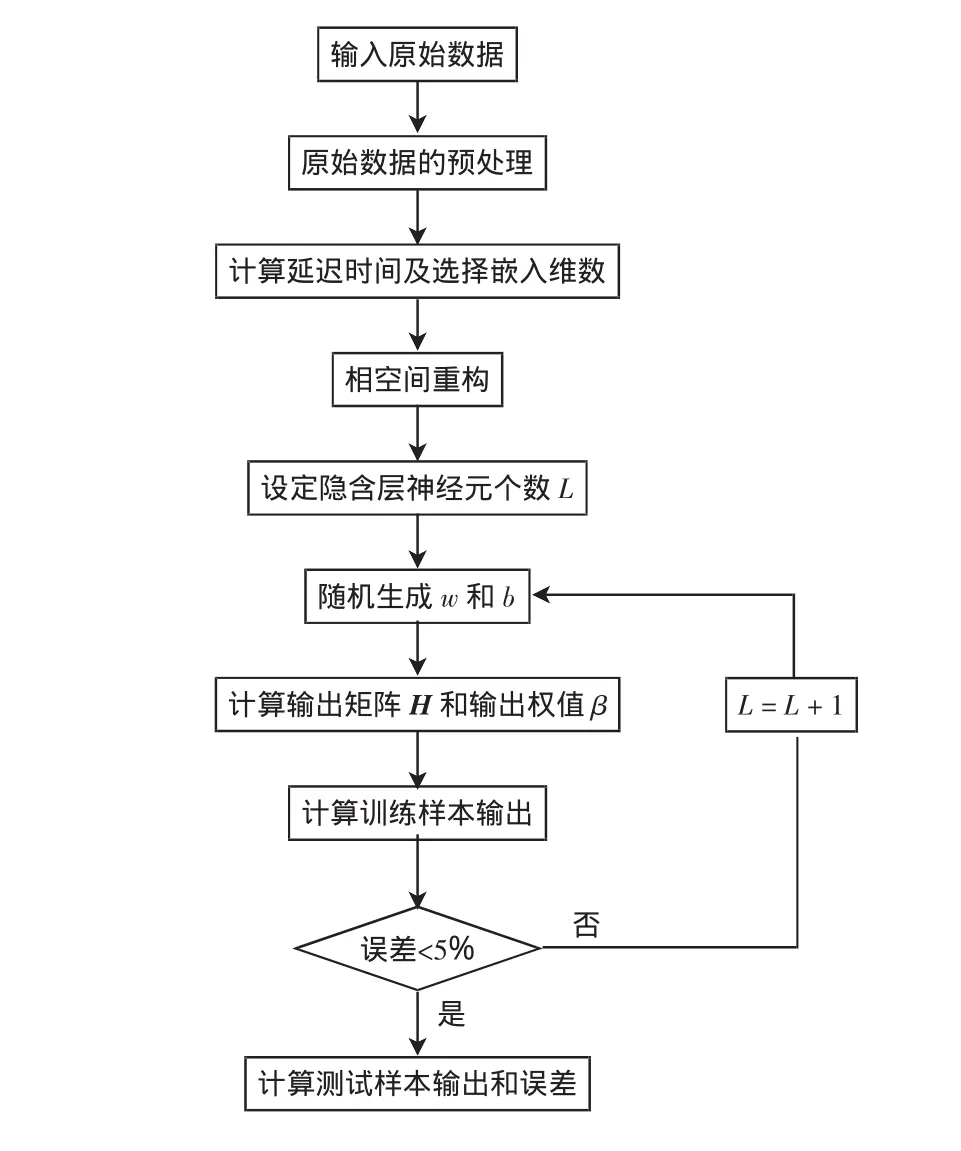
图1 相空间重构的ELM算法流程Fig.1 Flow chart of ELM algorithm with phase space reconstruction

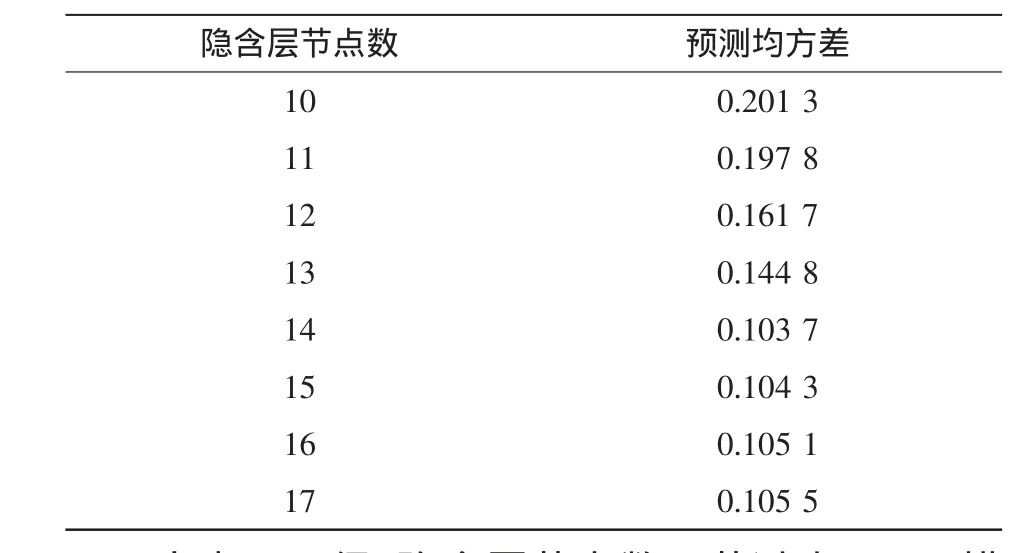
表1 不同数目的隐含层节点对应的预测均方差Tab.1 Predicted standard deviation in accordance with hidden nodes of different number

由表1可得，隐含层节点数目若过少，ELM模型不能很好地学习样本，即均方差很大；隐含层数目过多，泛化能力将变差，而且隐含层节点在14以后均方差都保持在0.103 7左右，因此本文选择隐含层节点数目为14。

ELM预测模型的预测风速值的分布如图2所示，预测结果如表2所示（由于数据较多，篇幅有限，只列取24个点数据）。

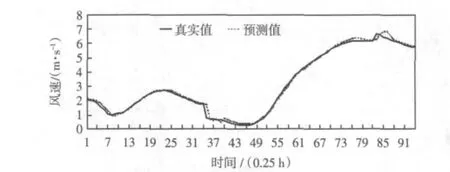
图2 实际风速与预测风速分布Fig.2 Distribution of forecasted and observed wind speed

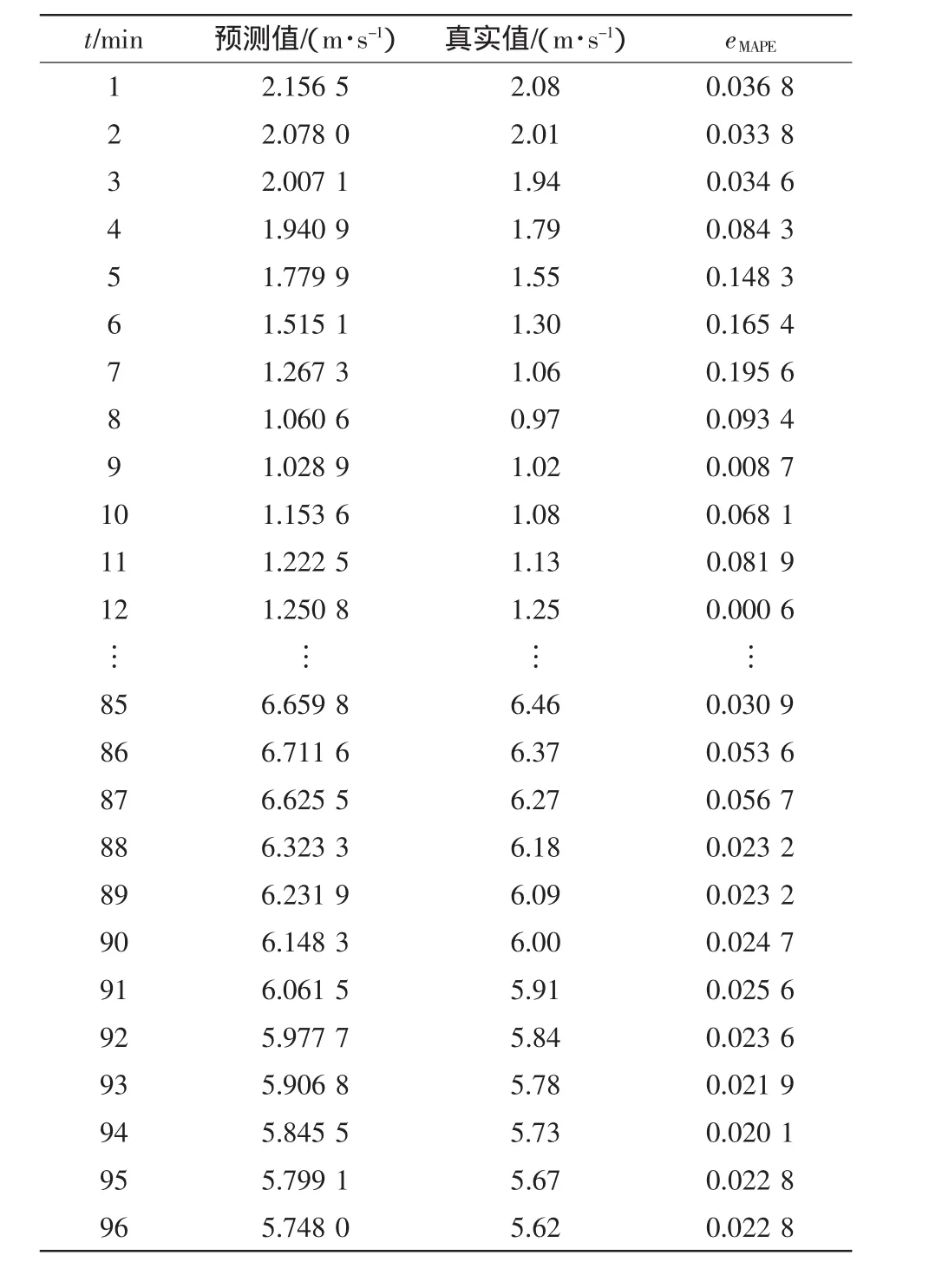
表2 ELM预测模型预测结果Tab.2 Forecasting results of ELM model

从图2和表2可以看出，ELM预测模型对风速提前15 min的预测只有少数点的相对误差较大，大部分预测点的预测较为准确，预测的最大误差、平均相对误差和均方误差分别为15.57%、7.201%和2.52%，结果比较理想，从而验证ELM理论在风速预测中的可行性。

将ELM模型与BP神经网络模型、支持向量机（support vector machine，SVM）模型的预测结果进行相应的比较，这些模型在数据处理上基本一样，这些模型得到的提前15 min的预测风速分布如图3所示，预测结果如表3和表4所示。

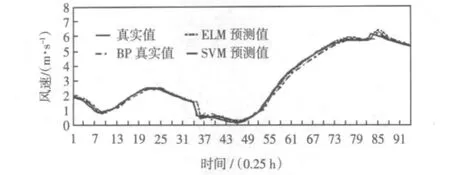
图3 不同模型的预测结果Fig.3 Distribution of wind speed forecasted by different model

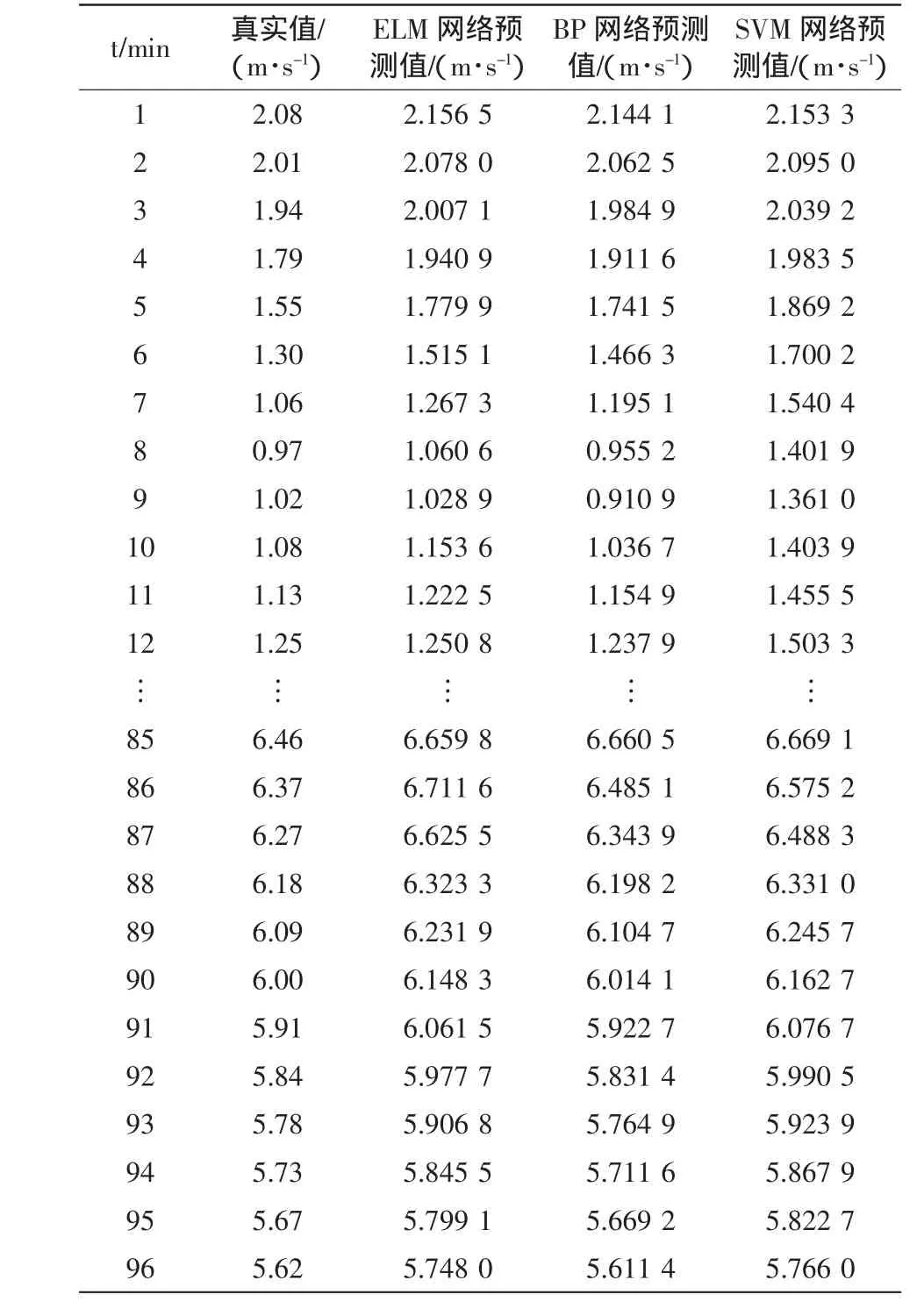
表3 不同模型预测风速值Tab.3 Forecasting wind speed results of different forecast model

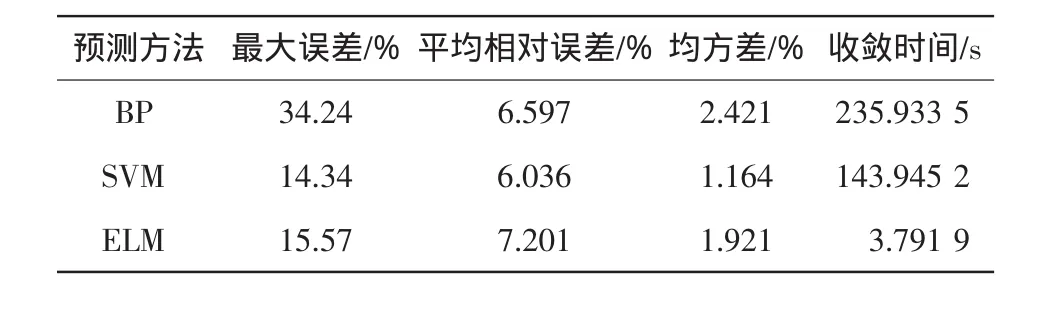
表4 不同模型预测结果Tab.4 Forecasting results of different forecast model

表3和表4分别列出不同预测模型的预测结果和预测误差。由不同模型得到的预测结果可以看出，SVM网络在风速预测中精度较高，预测效果较好，但是比ELM网络其优势并不是非常明显。从表3中的收敛时间可以看出，ELM网络几乎瞬间可以完成预测，而SVM网络所需要的时间约是它的37倍，BP网络需要的时间更多，因此ELM有明显的优势，所以在风速快速预测时，该方法可以达到更好的效果。然而，在实际应用中，不同的风电场有各自的特点，因此根据具体的情况来选择相应的方法才能取得理想的效果。

5 结语

本文运用混沌相空间重构理论，重构样本空间，使新的样本能够表征原始时间序列动态特性，更能反映风速变化特性，采用极端学习机进行了短期风速预测，并与BP网络和SVM网络进行对比，验证了极端学习机在风速预测中的优越性。极端学习机需要设置隐含层节点个数，参数选择容易，且在算法执行过程中不需要调整输入层与隐含层间的连接权值和隐含层神经元阀值，因此学习速度快、泛化性能好，为风速预测提供一种新方法。

[1]尹明，王成山，葛旭波（Yin Ming，Wang Chengshan，Ge Xubo）.风电并网经济技术评价研究综述（Review of economic technical assessment of wind power integration）[J].电力系统及其自动化学报（Proceedings of the CSUEPSA），2010，22（5）：102-108.

[2]Abdel-Aal R E，Elhadidy M A，Shaahid S M.Modeling and forecasting the mean hourly wind speed time series using GMDH-based abductive networks[J].Renewable Energy，2009，34（7）：1686-1699.

[3]丁明，吴义纯，张立军（Ding Ming，Wu Yichun，Zhang Lijun）.风电场风速概率分布参数计算方法的研究（Study on the algorithm to the probabilistic distribution parameters of wind speed in wind farms）[J].中国电机工程学报（Proceedings of the CSEE），2005，25（10）：107-110.

[4]陈国初，杨维，张延迟，等（Chen Guochu，Yang Wei，Zhang Yanchi，et al）.风电场风速概率分布参数计算新方法（New computation method of wind speed probability distribution parameters in wind farm）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（1）：46-51.

[5]蔡凯，谭伦农，李春林，等（Cai Kai，Tan Lunnong，Li Chunlin，et al）.时间序列与神经网络法相结合的短期风速预测（Short-term wind speed forecasting combing time series and neural network method）[J].电网技术（Power System Technology），2008，32（8）：82-85，90.

[6]李文良，卫志农，孙国强，等（Li Wenliang，Wei Zhinong，Sun Guoqiang，et al）.基于改进空间相关法和径向基神经网络的风电场短期风速分时预测模型（Multi-interval wind speed forecast model based on improved spatial correlation and RBF neural network）[J].电力自动化设备（Electric Power Automation Equipment），2009，29（6）：89-92.

[7]杜颖，卢继平，李青，等（Du Ying，Lu Jiping，Li Qing，et al）.基于最小二乘支持向量机的风电场短期风速预测（Short-term wind speed forecasting of wind farm based on least square-support vector machine）[J].电网技术（Power System Technology），2008，32（15）：62-66.

[8]曾杰，张华（Zeng Jie，Zhang Hua）.基于最小二乘支持向量机的风速预测模型（A wind speed forecasting model based on least squares support vector machine）[J].电网技术（Power System Technology），2009，33（18）：144-147.

[9]Damousis I G，Dokopoulos P.A fuzzy expert system for the forecasting of wind speed and power generation in wind farms[C]//International Conference on Power Industry Computer Applications.Sydney，Australia：2001.

[10]张智晟，马 龙，孙雅明（Zhang Zhisheng，Ma Long，Sun Yaming）.混沌理论和支持向量机结合的负荷预测模型（Load forecasting model using chaos theory and support vector machine）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2008，20（6）：31-35.

[11]韩敏.混沌时间序列预测理论与方法[M].北京：中国水利水电出版社，2007.

[12]郑永康，陈维荣，蒋刚，等（Zheng Yongkang，Chen Weirong，Jiang Gang，et al）.一种模糊支持向量的负荷混沌时间序列预测法（Chaotic time series method for load forecasting based on fuzzy support vector）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2007，19（6）：48-52.

[13]Huang Guang-Bin，Zhu Qin-Yu，Siew Chee-Kheong.Extreme learning machine：theory and applications[J].Neurocomputing，2006，70（1-3）：489-501.

[14]刘学艺，李平，郜传厚（Liu Xueyi，Li Ping，Gao Chuanhou）.极限学习机的快速留一交叉验证算法（Fast leave-one-out cross-validation algorithm for extreme learning machine）[J].上海交通大学学报 （Journal of Shanghai Jiao Tong University），2011，45（8）：1140-1145.

[15]潘华贤，程国建，蔡磊（Pan Huaxian，Cheng Guojian，Cai Lei）.极限学习机与支持向量机在储层渗透率预测中的对比研究（Comparison of the extreme learning machine with the support vector machine for reservoir permeability prediction）[J].计算机工程与科学（Computer Engineering&Science），2010，32（2）：131-134.

[16]Huang Guang-Bin，Chen Lei，Siew Chee-Kheong.Universal approximation using incremental constructive feedforward networks with random hidden nodes[J].IEEE Trans on Neural Networks，2006，17（4）：879-892.

[17]Takens F.Detecting strange attractors in turbulence[J].Lecture Notes in Math，1981，898（29）：366-381.

[18]张永明，齐维贵，王军栋（Zhang Yongming，Qi Weigui，Wang Jundong）.基于支持向量机的时间序列交叉负荷预报方法（Time series crossover load forecasting approach based on support vector machines）[J].电网技术（Power System Technology），2007，31（S2）：207-210.