基于细菌群体趋药性算法的配电网无功补偿优化

李学福，胡高峰，冯 光

（虞城县供电有限责任公司，虞城 476300）

配电网具有节点多、分支多、负荷分散等特点，因此配电网的电能质量往往得不到保证，配电网的无功补偿优化是解决这一问题的重要途径。通过配电网的无功补偿优化可以达到减小网损和提高电压稳定性等目的。

配电网的无功优化算法主要有线性规划法[1]、非线性规划法[2]、混合整数规划法和人工智能算法[3]。人工智能算法受初始点影响小，解决具有离散变量的优化问题更精确，鲁棒性好，人工智能算法主要包括遗传算法[4]和粒子群算法[5]等。细菌趋药性（BC）算法[6]是一种基于细菌趋药性微观模型而研究提炼出来的优化算法，是由美国人Muller综合了Bremermann等的研究成果提出的。文献 [7]在BC算法的基础上，加入了细菌的群体信息交互模式，进而提出了细菌群体趋药性（BCC）算法[7-9]。BCC算法将细菌由单个的个体转变成相互之间信息共享的种群，使算法性能上有了很大程度的提高。

本文用BCC算法确定无功补偿点的位置，以3种负荷方式来模拟配电网的运行状况并采用动态无功补偿装置[10]。分别计算最小、一般和最大3种负荷方式下的网络潮流，逐个确定3种负荷方式的补偿容量，并利用动态无功补偿装置的固定部分和可投切部分来实现不同负荷方式下的无功补偿[11]。最后对辐射型配电网络进行仿真测试，验证了BCC算法进行无功补偿的可行性。

1 数学模型

1.1 系统的整体数学模型

在配电网无功补偿计算中，可采取多种不同的目标函数。本文考虑无功补偿的经济性最好，所以以全年电能损失费用与无功补偿设备的投资费用之和作为目标函数。要求配电网在补偿后能在一个良好的状态下运行，电网需满足的约束条件有有功平衡和无功平衡、各节点电压不越界、系统各支路潮流约束等。系统的目标函数如下。

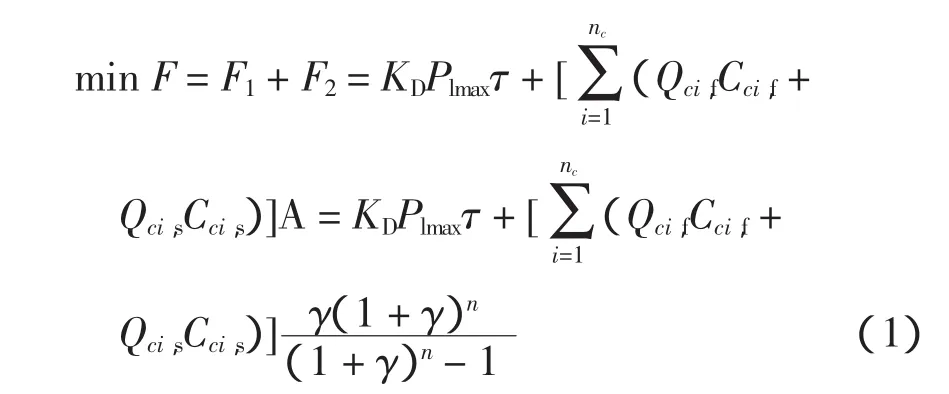
式中：KD为系统电价；Plmax为最大负荷方式下的网损；τ为最大负荷损耗时间；nc为无功补偿点的个数；Qci，f为i节点动态无功补偿装置固定部分的容量；Qci，s为i节点动态无功补偿装置可投切部分的容量；Cci，f为动态无功补偿装置固定部分单位容量投资费用系数；Cci，s为动态无功补偿装置可投切部分单位容量投资费用系数；γ为贴现率；n为设备寿命。

约束条件中的等式约束为系统的功率平衡，即

不等式约束为节点电压约束、无功补偿容量约束和支路潮流约束。

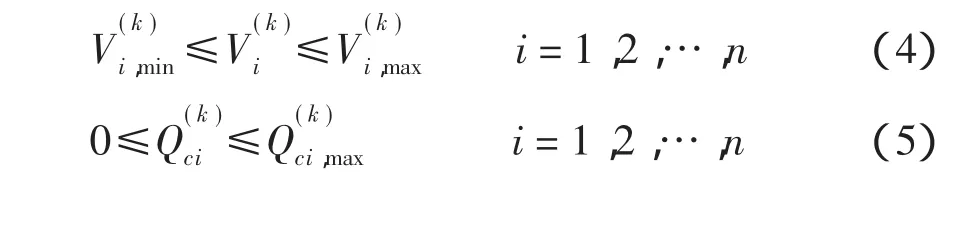
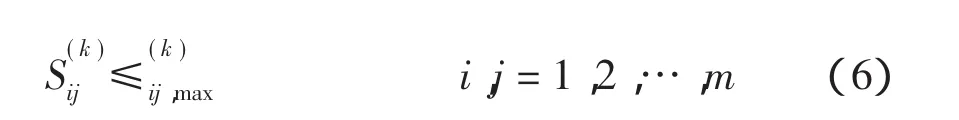
式中：上标 k=（1，2，3）分别代表最大、一般和最小3 种负荷方式；n 为节点个数；Qci，max为 i点可新增电容器补偿的最大容量。

1.2 数学模型的分解与协调

为了减少计算量，把整体优化问题分解为最大负荷方式、一般负荷方式和最小负荷方式3个子优化模型。对于系统新增无功补偿设备的投资费用仅在最大负荷方式子模型时考虑，用最大负荷损耗时间τ来协调统一。

1）最大负荷方式子模型

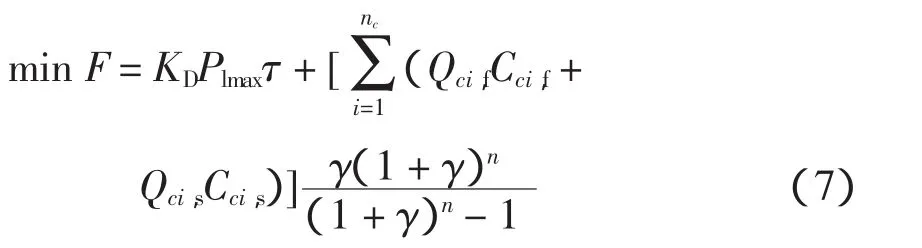
等式约束与不等式约束同式（2）～式（6）。

2）一般负荷方式和最小负荷方式的子模型

新增无功补偿设备的投资在最大负荷方式下计算。在一般和最小负荷方式下，将最大负荷方式下的设备作为现有补偿，不考虑投资问题，故一般和最小负荷方式下的数学模型分别为

2 细菌群体趋药性优化算法及无功补偿点的确定

2.1 算法步骤简述

1）单个细菌移动描述（细菌趋药性算法BC）

（1）选择移动方向。

细菌直线运动，第一次移动的方向为随机方向，之后的运动方向由（Φ1，Φ2，…，Φm-1）决定，其中Φi（i=1，2，…，m-1）由（i，i+1）这个二维空间内的高斯概率分布确定。Φi的概率分布为

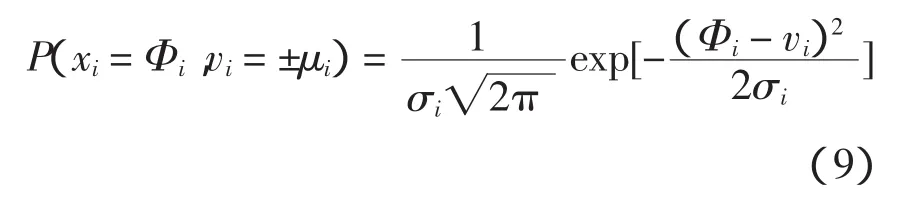
Φi在[0°，180°]范围内，方向向左或向右遵循一个统一的概率密度分布，因此

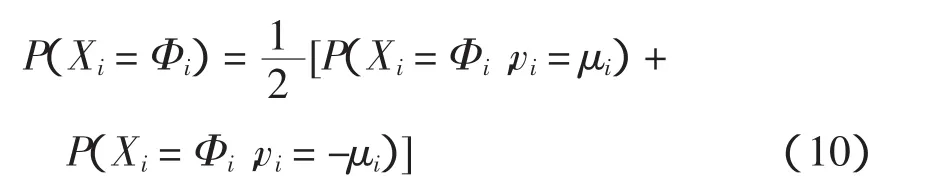
式中：下标 i=1，2，…，m 表示维度；Φi为向左或向右的角度值；x、v、μ、σ为高斯概率密度分布参数，μ为期望，σ为方差。β为当前点与上一点的目标函数值之差，则当β＜0时有

式中：τpr为细菌上一运动轨迹的持续时间；τc为相关时间。

β＞0 时有 μ =62°，σ =26°。

确定了（Φ1，Φ2，…，Φm-1）以后，将（Φ1，Φ2，…，Φm-1）与以前的移动角度求和，就可以得到一个新方向矢量nn，即细菌新的移动方向。

（2）确定移动距离。

在确定移动距离时，以细菌在n维空间中的位置坐标（L1，L2，…，Ln）来描述细菌的位置。移动步长为（l1，l2，…，ln），则有

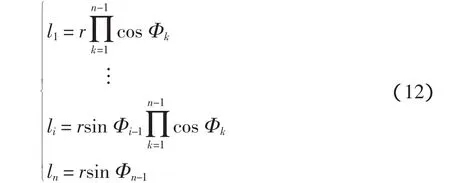
式中，r为细菌的移动半径。

BC算法是一种随机梯度近似的搜索方法，由于运动方向的随机性以及运动方向和距离受到上一步运动的很大影响等原因。BC算法的寻优速度较慢，并且比较容易偏离最优解。

2）细菌群体信息交互模式（细菌群体趋药性算法BCC）

由于BC算法有许多局限性。为了进一步的优化算法，产生了基于细菌群体信息交互模式的细菌群体趋药性算法（BCC）。在群体信息交互模式下细菌的移动方向和移动距离分别应满足条件。

（1）在每次移动完成后，位置最好的细菌坐标称为中心坐标，其他位置的细菌下次移动的方向为向中心坐标移动。

（2）细菌的移动长度为CrandIdis，其中Idis为细菌与更优点细菌之间的距离。Crand为（0，2）之间服从均匀分布的随机值。

在每次移动后，都要寻找中心坐标，确定下次每个细菌的移动方向和移动距离，当寻优结果满足开始设定的精度要求时完成寻优，若不满足条件则细菌群继续移动。

2.2 算法的改进策略

细菌在移动的过程中，由于移动方向和移动距离具有一定的随机性，每次移动后产生的最优个体，在下次移动时有一定概率偏离寻优方向，这样的寻优速度较慢，因此采用如下策略，在细菌群体完成一次移动之后，位置最差（目标函数值最大）的细菌直接移动到位置最好（目标函数值最小）的细菌的位置。这样可以增大最优个体按照最佳寻优方向移动的概率，有效的减少整个寻优过程中细菌群体移动的总次数。

2.3 无功补偿候选点的确定

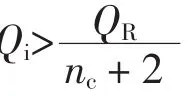
2.4 无功补偿点的确定

应用细菌群体趋药性算法进行仿真计算，确定补偿点。设细菌个数为n，细菌坐标变量的维数由无功补偿装置控制变量个数m来决定，本文采用在节点进行补偿，所以m的值等于可装设无功补偿装置的节点数目，细菌遵循在m维空间中的移动规律进行寻优。

3 潮流计算

配电网一般为辐射型网络，采用前推回代法进行潮流计算。前推回代法分为前推和回代两个部分，前推部分从网络末端向根节点进行推算，仅计算支路的功率损耗而不计算电压降落，求得始端功率。电压在第一次前推计算时采用额定值，第二次和以后计算时采用回代算出来的值。

图1为i，j节点间的潮流计算，前推计算的计算公式为

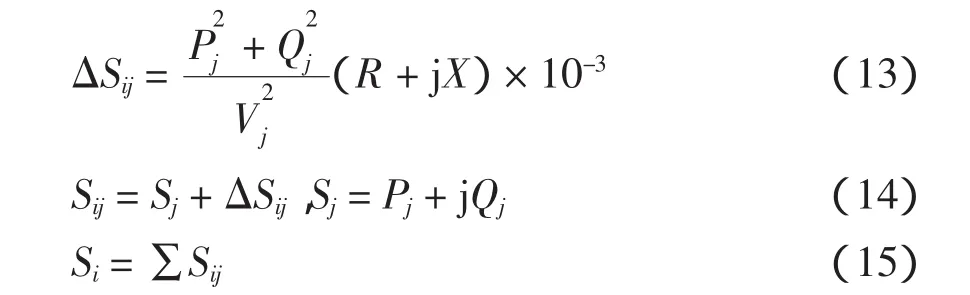
回代部分运用给定的始端电压和已得的始端功率向末端推算电压降落，回代过程不再计算功率损耗。计算公式为

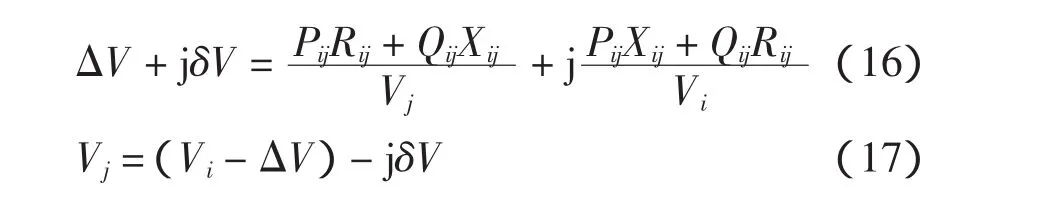
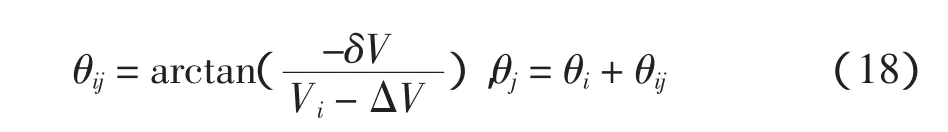
重复上述计算过程，直到连续两次计算得到的节点电压满足约束条件。

式中：k为潮流计算的迭代次数。

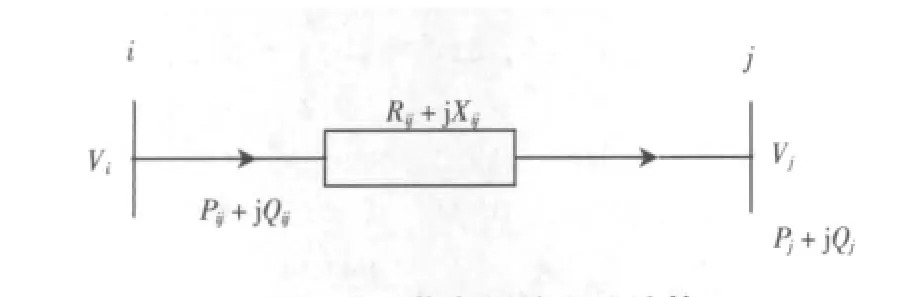
图1 i，j节点间的潮流计算Fig.1 i，j node power flow calculation

4 无功补偿容量的确定及设备的选取

在潮流计算的过程中按照减少线路损耗的原则来进行补偿。对于节点i，最优的无功补偿量大小等于计算功率Qi。在实际确定无功补偿量时应满足约束条件：

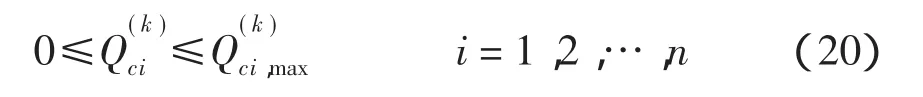
节点电压和各支路潮流也需要满足约束条件

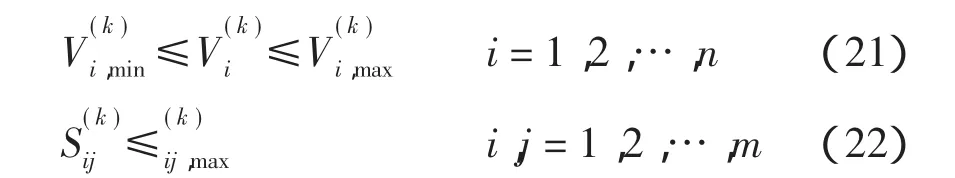
若节点电压或支路潮流出现越限的情况，则应改变无功补偿量的大小，重新进行潮流计算，使补偿结果满足所有约束条件。

本文补偿设备采用动态无功补偿电容器，动态无功补偿电容器由两部分组成：固定部分和可投切部分。最小负荷方式下仅投入固定部分，一般负荷方式下投入固定部分和可投切补偿装置的一部分，最大负荷方式下投入固定部分和全部可投切部分。

5 模型的总体求解步骤

模型的总体求解步骤如下所述。

步骤1 输入系统的原始数据：系统信息（节点数、支路数、无功补偿节点数等）、节点信息（节点负荷、电压上下限等）等。

步骤2 随机产生50个细菌，构成初始细菌群。迭代次数记为0。

步骤3 对于（2）中产生的细菌个体进行潮流计算，分别求出在最小负荷方式、一般负荷方式和最大负荷方式下各个初始补偿节点的补偿容量。确定可投切无功补偿设备固定部分和可投切部分的补偿容量。并求出补偿后3种运行方式的网损，最后求出目标函数的数值，进行比较得到群体最优解。

步骤4 更新细菌的移动方向和细菌位置：按照BCC算法中细菌移动方向的公式，来确定每个细菌的新的移动方向，并乘以移动的速度，得到新的细菌位置。检查细菌位置更新后各变量是否越限，若出现越限现象则取其限值，防止细菌超出可行搜索区域。

步骤5 对于更新后的细菌进行潮流计算，重新确定补偿容量，并计算补偿后3种负荷方式下的网损，比较目标函数的数值，更新群体最优解。

步骤6 判断最优解是否满足终止寻优的约束条件，即前后两次计算的目标函数值之差小于给定的终止精确度εend，如果满足约束条件则执行步骤7，否则转至步骤4继续进行计算，如果达到迭代次数也转至步骤7。

步骤7 输出结果。

6 算例

本文以24节点算例（图2）为例，对其进行仿真计算。设定每组动态无功补偿电容器的固定部分综合投资为8万元/Mvar（包括维护、管理等费用），可投切部分的综合投资为12万元/Mvar，补偿设备有效使用年限取为20 a，贴现率取为0.1，电价取为0.06万元/（MW·h）。节点电压的合格范围为9.5 kV～10.5 kV。系统年运行时间按8 760 h计算，最大负荷方式和最小负荷方式的运行时间均为2 190 h，一般负荷方式的运行时间为4 380 h。满足条件的的无功补偿候选点为 2，3，4，5，6，7，8，11，18，19。

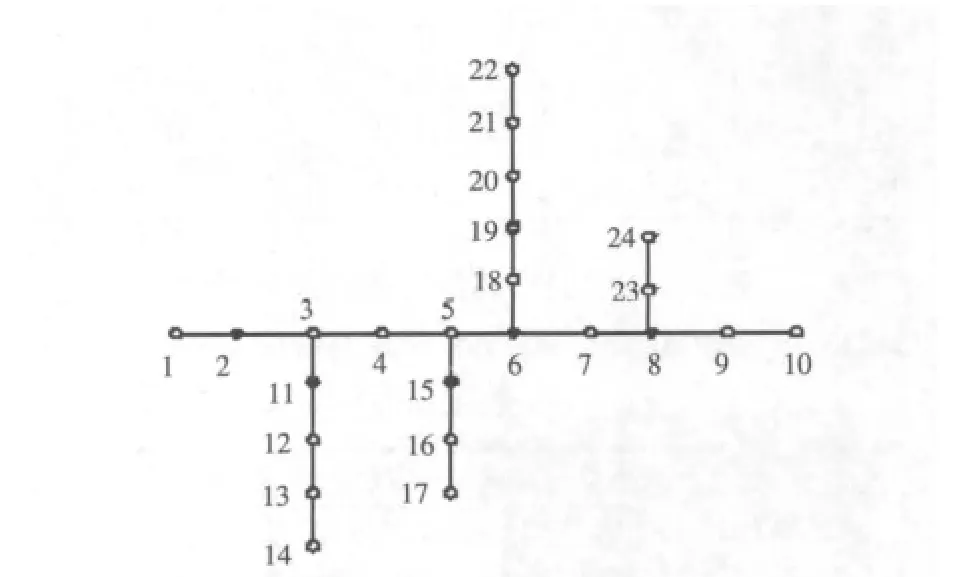
图2 24节点配电网结构Fig.2 Structure of 24-node distribution network

图3的横轴为细菌的移动次数，纵轴为目标函数的数值。本文通过加入改进策略，在每次移动后都将位置最差的细菌移动到位置最好的细菌的位置，使得寻优速度得到加快。对于本算例，BCC算法通过73次寻优得到最优解，在引入改进策略以后，经过51次移动即可得到最优解，在一定程度上提高了计算效率。

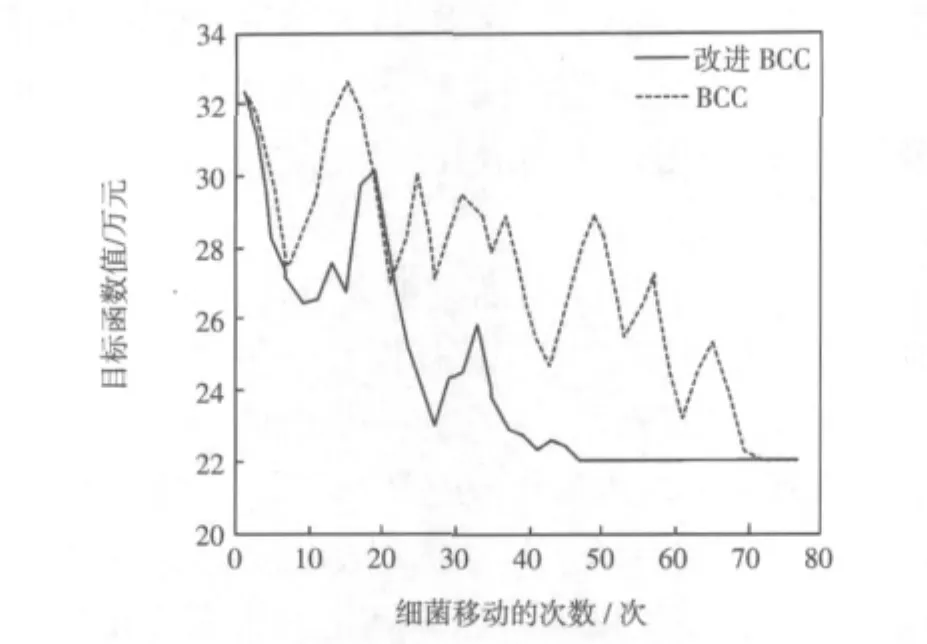
图3 算法的目标函数变化对比Fig.3 Comparison between BCC and improved BCC

从表1和表2中可以看出，在应用了动态无功补偿装置以后，3种负荷方式下的网损均有明显的降低，目标函数值也有明显的降低，说明通过无功补偿，电能质量得到了改善，同时也获得了一定的经济效益。

从表3可见补偿后各节点电压标幺值均有明显的增加，3种负荷方式下的所有节点电压都满足约束条件。

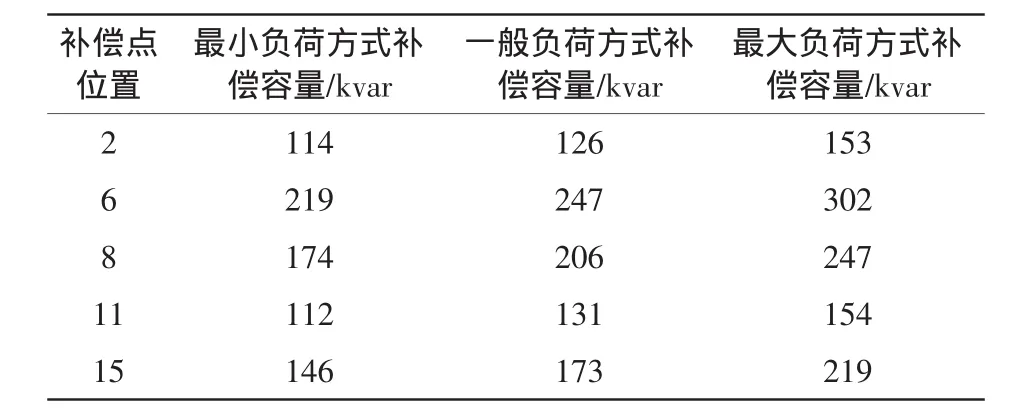
表1 补偿点和3种负荷方式下的补偿容量Tab.1 Capacities of the dynamic reactive power compensation device

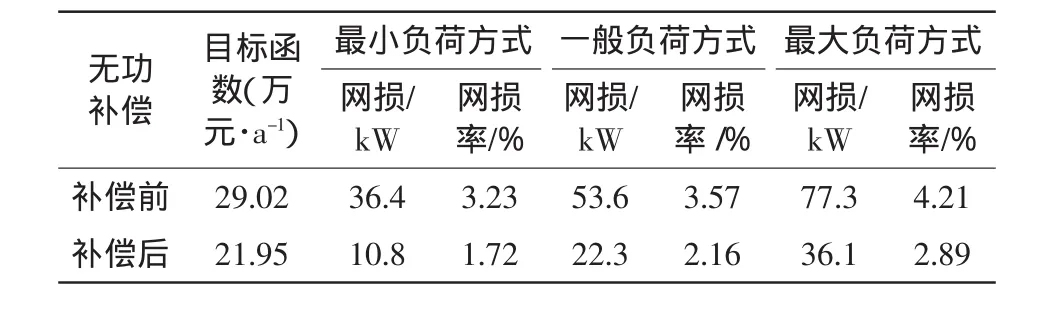
表2 补偿前后的运行费用及网损Tab.2 Operating cost and network loss before and after compensation

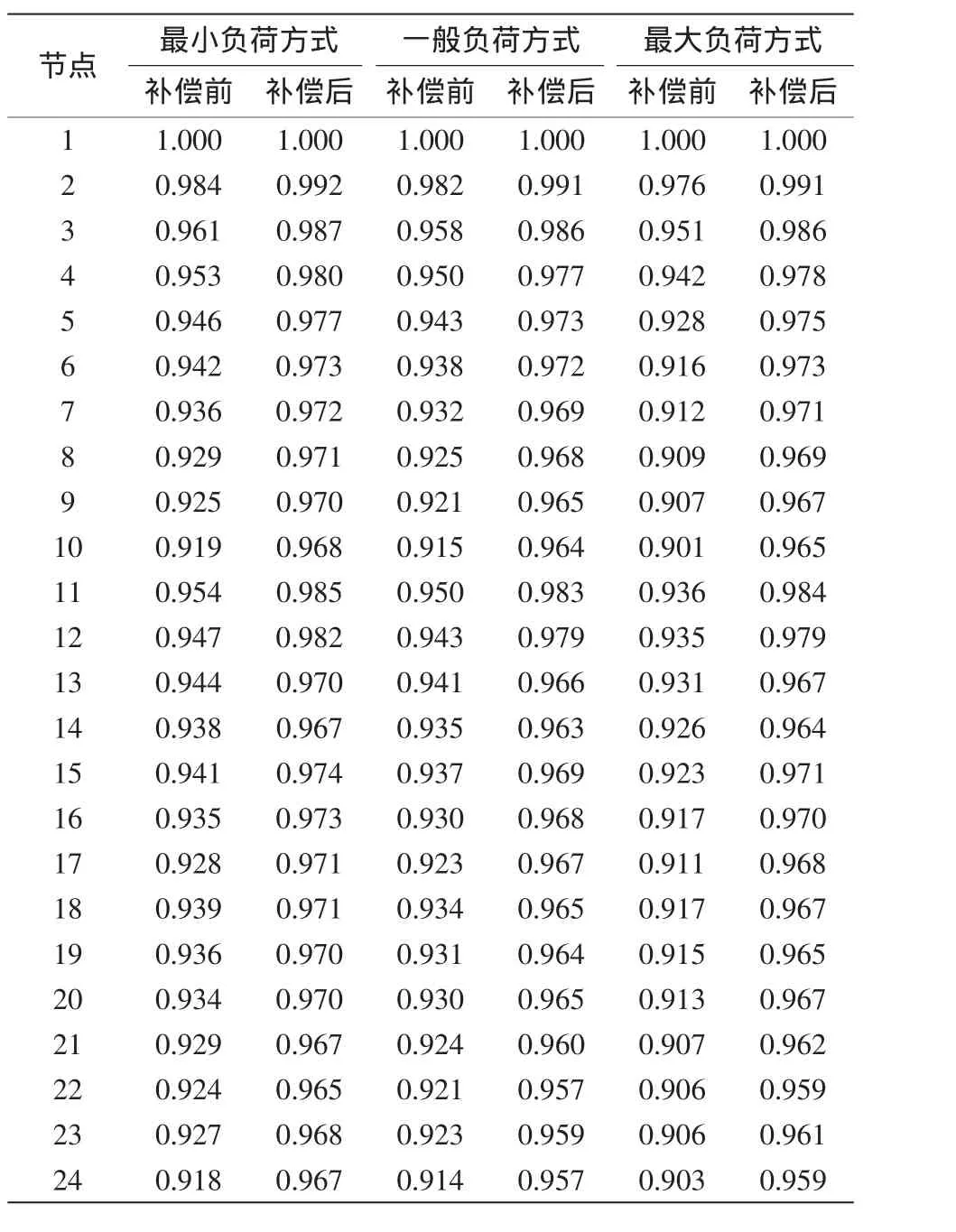
表3 补偿前后各节点电压Tab.3 Node voltages before and after compensation

7 结语

本文的目标函数同时考虑了动态无功补偿设备的投资费用和配电网的网损，在经济评价方面更合理。应用细菌群体趋药性优化算法确定无功补偿点的位置，并通过对算法进行改进，使得寻优速度得到提升。利用动态无功补偿装置，可以对三种负荷方式分别进行补偿，使得三种负荷方式下的网损都得到很大程度的降低。对算例的计算结果表明，本文所提到的方法用于处理配电网无功优化问题，可以得到较好的结果。

[1]Urdaneta A J，Gomez J F，Sorrentino E，et al.A hybrid ge netic algorithm for optimal reactive power planning based upon successive linear programming[J].IEEE Trans on Power Systems，1999，14（4）：1292-1298.

[2]Hua Wei，Sasaki H，Kubokawa J，et al.An interior point nonlinear programming for optimal power flow problems with a nove1 data structure[J].IEEE Trans on Power Systems，1998，13（3）：870-877.

[3]许文超，郭伟（Xu Wenchao，Guo Wei）.电力系统无功优化的模型及算法综述（Summarize of reactive power optimization model and algorithm in electric power system）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2003，15（1）：100-104.

[4]周晓娟，蒋炜华，马丽丽（Zhou Xiaojuan，Jiang Weihua，Ma Lili）.基于改进遗传算法的电力系统无功优化（Reactive power optimization of power system based on improved genetic algorithm） [J].电力系统保护与控制（Power System Protection and Control），2010，38（7）：37-41.

[5]张斌（Zhang Bin）.基于粒子群算法的配电网无功补偿优化规划（Reactive power compensation of distribution network based on particle swarm optimization）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2010，22（2）：157-160.

[6]Muller S D，Marchetto J，Airaghi S，et al.Optimization based on bacterial chemotaxis[J].IEEE Trans on Evolutionary Computation，2002，6（1）：16-29.

[7]李威武，王慧，邹志君，等（Li Weiwu，Wang Hui，Zou Zhijun，et al）.基于细菌群体趋药性的函数优化方法（Function optimization method based on bacterial colony chemotaxis）[J].电路与系统学报（Journal of Circuits and System），2005，10（1）：58-63.

[8]黄伟，张建华，张聪，等（Huang Wei，Zhang Jianhua，Zhang Cong，et al）.基于细菌群体趋药性算法的电力系统无功优化（Reactive power optimization in power systems based on bacterial colony chemotaxis algorithm）[J].电力系统自动化（Automation of Electric Power Systems），2007，37（7）：29-33.

[9]刘文霞，刘晓茹，张建华，等（Liu Wenxia，Liu Xiaoru，Zhang Jianhua，et al）.基于微分进化和混沌迁移的细菌群体趋药性算法（Bacterial colony chemotaxis algorithm based on differential evolution and chaos migration）[J].控制 理 论 与 应 用 （ Control Theory&Applications），2009，26（4）：353-357.

[10]刘甲庆，张浩，章健（Liu Jiaqing，Zhang Hao，Zhang Jian）.中压配电网计及动态无功补偿装置的理论线损计算（Theoretical line loss calculation on medium voltage distribution with dynamic reactive power compensation devices）[J].电力系统保护与控制（Power System Protection and Control），2010，38（6）：92-95，140.

[11]李林川，刘娜，顾丽梅（Li Linchuan，Liu Na，Gu Limei）.考虑静态电压稳定裕度的配电系统无功补偿优化配置（Structure design of output filter in STATCOM and its parameter optimization）[J].电工技术学报（Transactions of China Electrotechnical Society），2008，23（4）：119-124，142.