基于两种改进方法的电能质量综合评估

何吉彪，程浩忠，姚良忠，Masoud Bazargan

（1.上海交通大学电气工程系电力传输与功率变换控制教育部重点实验室，上海 200240；2.国网电力科学研究院，南京210061；3.阿尔斯通电网集团研究与技术中心，斯塔福德ST17 4LX，英国）

我国现有七项电能质量标准，分别对电压偏差、频率偏差、谐波、间谐波、电压三相不平衡度、电压波动与闪变、暂时过电压和瞬态过电压进行了限定，且目前电能质量测量仪能够判断这些电能质量指标是否满足标准要求[1]。但如何从总体上对电能质量做出综合评价现在仍然是研究的难点和热点之一。

文献[2]在国家标准规定的相关电能质量指标限值基础上，建立了同一尺度下的统一型电能质量指标体系，提出了一种基于雷达图法的电能质量综合评估方法。文献[3]通过主观权重和客观权重的组合来构建电能质量的综合指标，但其客观权重的确定方法还值得商榷。文献[4]用二阶段线性规划的方法得到各项指标权值，然后采用概率统计的方法将各项指标综合量化，得到综合评价电能质量的唯一量化指标。文献[5]构造出模糊神经识别网络，构建了电能质量综合评估的模糊神经网络模型。目前的电能质量评估方法逐渐趋向于复杂化，在实际推广应用中可能会造成一定的困难。

本文通过分析AHP中判断矩阵的不一致性与比较矩阵的关系，调整对一致性影响最大的元素，得到合理的权值。分别以电能质量国标中的规定值和限制值作为加权TOPSIS的绝对理想解和绝对负理想解，改进了加权TOPSIS法只对各个评价对象排序而无法进行定性分级的不足，同时解决了逆序的问题。该综合评估方法操作简便易行，可以根据不同类型的负荷的敏感程度来确定各单项指标的不同权重，所得评估结果客观，合理。

1 层次分析法和加权TOPSIS法的改进

1.1 层次分析法的改进

层次分析法是一种定性与定量相结合的决策分析方法。它的基本思路可以分为以下4个步骤。

（1）将复杂的问题层次化，形成由目标层、准则层、指标层和方案层组成的递阶层次结构；

（2）采用“1-9标度法”，规则如表1所示，形成判断矩阵；

（3）检验判断矩阵的一致性；

（4）通过逐层计算，得到方案层对目标层的权重，确定出最优方案。

表1 判断矩阵标度及含义Tab.1 Scale and meaning of judgment matrix

AHP法的关键是要给出一个具有一致性的判断矩阵A=（aij）n×n。通过设定一个比较矩阵P，可对影响最大的元素进行微调，改进判断矩阵的一致性。

改进判断矩阵一致性的方法步骤如下。

步骤1 由评估专家给出判断矩阵An×n的上三角元素，根据aij=1/aji的准则确定下三角元素，保证A为正互反矩阵；

步骤2 计算判断矩阵A的排序权值ω；

步骤3求出比较矩阵P=（pij）n×n，

令

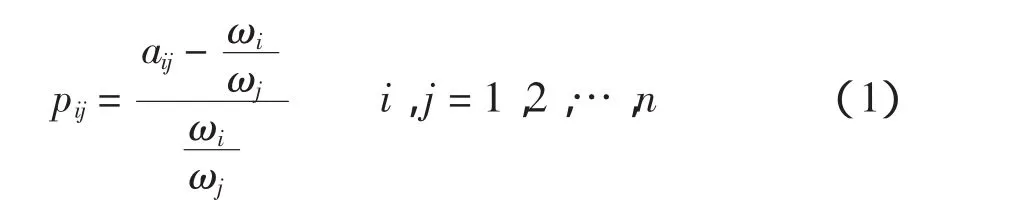
称矩阵P=（pij）n×n为判断矩阵A的比较矩阵；

步骤4 将矩阵P中绝对值最大的元素pij的下标 i，j对应记为 s，t；

步骤5 当pst>0时，若ast为整数，令ast′=ast-1，若ast为分数，令ast′=1/（1/ast+1）；

当 pst<0 时，若 ast为整数，令 ast′=ast+1，若 ast为分数，令ast′=1/（1/ast-1）；

步骤6 令 ats′=1/ast′，aij′=aij，i，j=1，2，…，n且 i，j≠s，t；

（7）计算新生成矩阵 A′=（aij′）n×n的 CR 值，若CR（A′）<0.1，A′即为所求；否则，将矩阵 A′代入步骤1继续求解。

进行上述求解步骤的原因是矩阵A为完全一致性矩阵的充要条件是矩阵P中元素全部为0，即pij=0。因为，若判断矩阵A为完全一致性矩阵，则有 aij= ωi/ωj，从而 pij=0（i，j=1，2，…，n）；若有 pij=0（i，j=1，2，…，n），从而 aij= ωi/ωj，即 A 为完全一致性矩阵。

由此可知，判断矩阵A是否为完全一致性矩阵可由P中是否存在不为0的元素判断。aij对A的不一致性的影响越大则对应的pij偏离0越大。一般情况下，专家给出的判断矩阵不会出现较大偏差，可通过对影响最大的元素增减1来逐步改进判断矩阵的一致性。当pij>0时，aij偏大，应该减小；当pij<0时，aij偏小，应该增大。

1.2 加权TOPSIS法的改进

1.2.1 加权TOPSIS法及逆序问题

在多指标的决策问题中，TOPSIS法是一种逼近理想解的排序方法，借助于多指标问题中的正理想解和负理想解对方案集中的各方案进行排序。在欧氏空间中，离正理想解距离越近、而离负理想解距离越远的方案越优。正理想解是方案集中并不存在的虚拟的最佳方案，其每个指标值都是决策矩阵中该指标的最优值；负理想解则是虚拟的最差方案，其每个指标值都是该指标的最差值。而加权TOPSIS法强调了参与评估的各指标重要性的不同，使评价结果更趋合理。

逆序是指当使用加权TOPSIS法时，n个方案x1，x2，…，xn的评价结果是方案xi优于xj（i≠j），但是当增加（或减少）若干个方案后，得出的结果却是方案xj优于xi，这就是逆序问题[7]。逆序问题将使得原来所做的所有工作（包括最后的决策结果）都变得毫无意义。

假设有两个指标均为高优指标，每一个属性的权值相等，即w1=w2=0.5；设有5个可行方案，分别为

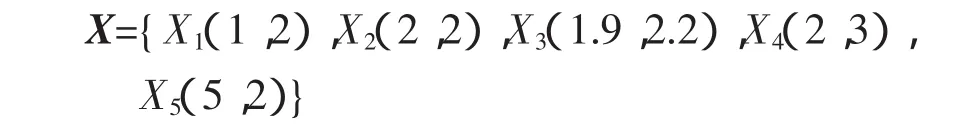
按照传统的TOPSIS法进行计算，当考虑前4个方案时，规范化预处理各方案的原始数据，有

最后的排序结果为

当考虑5个方案时，对方案的原始数据进行规范化预处理，有

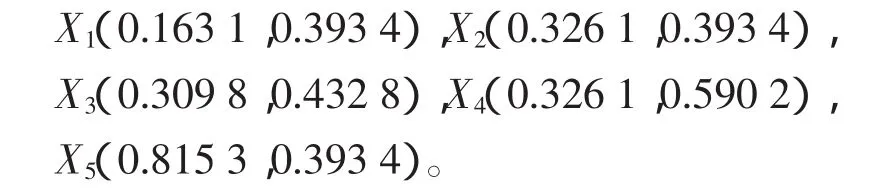
最后的排序结果为

由上面两次的结果可知，X2和X3在方案增加前后的排序不同，即出现了逆序。对于给定的两组方案的数据，虽然指标值的变化都是保序变化，但是在两次决策中的理想解是不同的。在只有前4个方案的方案集中，多指标问题的正理想解为（0.563 4，0.642 0），负理想解为（0.281 7，0.428 0）；当方案集中有5个方案时，多指标问题的正理想解为（0.815 3，0.590 2），负理想解为（0.163 1，0.393 4）。可见方案的增加（或减少）造成的影响是引起了正理想解、负理想解和参照标准的改变，从而可能导致逆序的产生。

如果简单地将加权TOPSIS法应用于电能质量的综合评估，除了存在逆序问题之外，还有一个问题是，它只能对各个评估对象进行排序，选出电能质量较好的一个，但是不能评估其好坏程度，无法与电能质量的国标值联系，以国标值为参考进行评估。

1.2.2 加权TOPSIS法的改进

由上述分析可知，正理想解和负理想解的改变是TOPSIS法产生逆序的一个很重要的原因。为了克服这一缺点，引入绝对正理想解和绝对负理想解，同时结合电能质量评估的特点，将电能质量国标中的规定值作为绝对正理想解，限制值作为绝对负理想解，添加到评价对象的数据矩阵中一起进行运算处理，不仅可以对各评估对象进行排序，克服逆序问题，还能以国标为准则判断对象是否合格并进行定性分级。

改进后的加权TOPSIS法的步骤如下。

（1）以电能质量国标中的规定值为理想解，限制值为负理想解；

（2）将理想解和负理想解指标与各评估对象的数据一起进行同趋势化和归一化处理；

（3）计算理想解与负理想解之间的距离D；

（4）计算各评估对象与理想解和负理想解间的距离Di+和Di-；

（5）计算各评估对象与理想解的接近程度Ci；

（6）根据D与Di+的关系判断评价对象是否合格，由Ci对合格的评估对象进行分级评估。

2 基于改进AHP和加权TOPSIS法的电能质量综合评估

上文对层次分析法和加权TOPSIS法的改进进行了阐述，基于两者的电能质量综合评估的具体方法如下。

假设针对m个评估对象的电能质量情况进行综合评估，评价的电能质量指标类型为n个，则数据矩阵为 Xm×n。

（1）运用改进的AHP法求解各电能质量指标的权值，得到权值相量 ω =（ω1，ω2，…，ωn）T。

（2）将n个电能质量指标对应的国标中的规定值和限制值分别设定为理想解和负理想解。

（3）数据的同趋势化和归一化。

将理想解与负理想解加入到评估对象的指标数据矩阵中，得矩阵为 X（m+2）×n。

一般的电能质量指标为低优指标，如频率偏差、闪变、谐波畸变率等，都是数值越小越好。如果有不同趋势的指标，可用倒数法或插值法将所有指标同趋势化，所得矩阵为 X′（m+2）×n。

同趋势化后，为了消除计量单位的影响，需要按照式（2）进行向量归一化处理，得到归一化矩阵Z中元素为

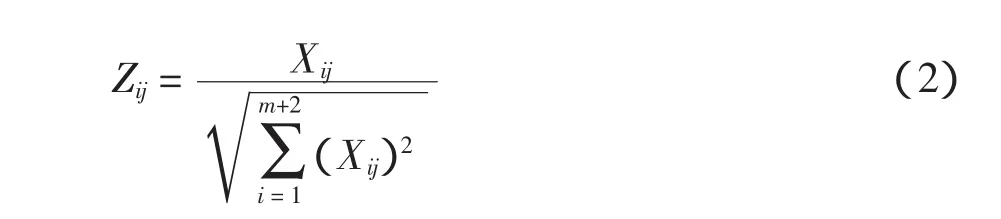
分别用 Z+=（Z1+，Z2+，…，Zn+）和 Z-=（Z1-，…，Zn-）表示评价指标的理想解与负理想解。+为处理后的第j个电能质量指标的国标规定值为处理后的第j个电能质量指标的国标限制值。

（4）计算理想解与负理想解之间的距离D。

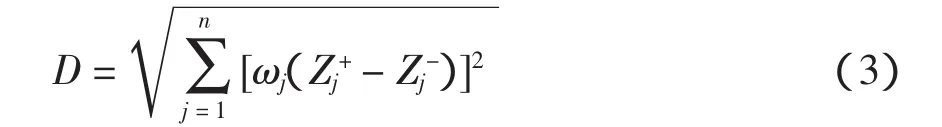
（5）计算各评估对象的指标值与理想解及负理想解之间的距离和，计算公式为

（7）计算合格的评估对象与理想解的接近程度为

图1 电能质量综合指标分级Fig.1 Grading of power quality comprehensive indexes

3 实例应用分析

用本文提出的电能质量综合评估方法对两个光伏发电系统的电能质量情况进行评估。这两个光伏发电系统分别安装于两个110 kV变电站的站用电系统中，系统A容量为4.8 kW，系统B容量为30 kW。评估的基础为在光伏发电系统并网点测得的实际数据。

案例中选取的电能质量指标为两个系统的电能质量测量结果中共有的指标，包括电压偏差、闪变、谐波畸变率、三相不平衡度、频率偏差；经过专家调查，按表1规则给出判断矩阵A。如果采用更多的单项评估指标，可采用相同的方法进行评估，只是判断矩阵的维数不同。

用第1.1节的方法求得的权重相量为

ω =（0.1844 0.1063 0.4589 0.1844 0.0660）T

将两个光伏发电系统测得的各项电能质量指标数据与国标规定值和限制值一起同趋势化和归一化后，所得的矩阵为

其中第一行为理想解，最后一行为负理想解。

用式（3）～式（5）计算得到两个光伏发电系统的电能质量评估结果如表2所示。

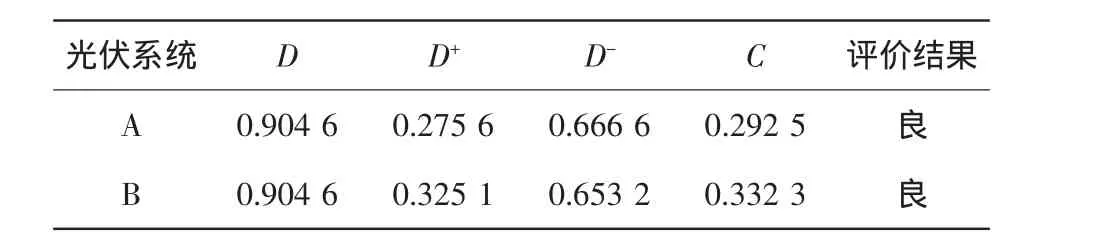
表2 评估结果Tab.2 Results of evaluation

首先两个系统的D+值均小于D值，表明两个系统的指标值均合格。再根据图1的分级标准，两个光伏发电系统的电能质量综合评估结果均为良。系统A的C值小于系统B的C值，说明系统A的电能质量综合评估结果比系统B更接近于国标的规定值，更远离国标的限制值，所以光伏发电系统A的电能质量综合情况优于系统B。系统A的容量小于系统B，评估结果说明了光伏发电系统容量增大将对所接入的电网的电能质量造成更大的影响，体现了该方法的合理性。

4 结论

（1）通过分析判断矩阵的不一致性与比较矩阵的关系，简单有效地改进了判断矩阵的一致性，得到更为合理的指标权重。

（2）将电能质量国标的规定值设为理想解，限制值设为负理想解，解决了将加权TOPSIS法应用于电能质量评估时可能产生的逆序问题，以及弥补了只对各个评价对象排序而无法进行定性分级的不足，结合改进AHP所得的权值，使得评估方法更加简便，具有实用性。

（3）通过案例的实际应用，得到了综合性的分级评估结果，证明了这种方法的简便易行，可以客观、全面、合理地对评估对象的电能质量进行综合评估，具有较好的应用价值。

[1]谭家茂，黄少先（Tan Jiamao，Huang Shaoxian）.基于模糊理论的电能质量综合评价方法研究（Research on synthetic evaluation method of power quality based on fuzzy theory）[J].继电器（Relay），2006，34（3）：55-59.

[2]李国栋，李庚银，杨晓东，等（Li Guodong，Li Gengyin，Yang Xiaodong，et al）.基于雷达图法的电能质量综合评估模型（A comprehensive power quality evaluation model based on radar chart method）[J].电力系统自动化（Automation of Electric Power Systems），2010，34 （14）：70-74.

[3]刘兵，李群湛，董祥（Liu Bing，Li Qunzhan，Dong Xiang）.基于时变权重的电能质量综合评估研究（Comprehensive assessment study of the power quality based on the timevarying weight）[J].电力系统保护与控制（Power System Protection and Control），2009，37（14）：6-9.

[4]熊以旺，程浩忠，王海群，等（Xiong Yiwang，Cheng Haozhong，Wang Haiqun，et al）. 基于改进 AHP 和概率统计的电能质量综合评估（Synthetic evaluation of power quality based on improved AHP and probability statistics）[J].电力系统保护与控制（Power System Protection and Control），2009，37（13）：48-52，71.

[5]周林，栗秋华，刘华勇，等（Zhou Lin，Li Qiuhua，Liu Huayong，et al）.用模糊神经网络模型评估电能质量（E－valuation of power quality by fuzzy artificial neural network）[J]. 高电压技术 （High Voltage Engineering），2007，33（9）：66-69.

[6]陶顺，肖湘宁（Tao Shun，Xiao Xiangning）.电力系统电能质量评估体系架构（Infrastructure of the power quality assessment system of power systems）[J].电工技术学报（Transactions of China Electrotechnical Society），2010，25（4）：171-175.

[7]黄德才，郑河荣（Huang Decai，Zheng Herong）.理想点决策方法的逆序问题与逆序的消除（Study on the problem and elimination of rank reversal existing in ideal point multiple attribute decision making）[J].系统工程与电子技术（Systems Engineering and Electronics），2001，23（12）：80-83.

[8]张弛，程浩忠，奚珣，等（Zhang Chi，Cheng Haozhong，Xi Xun，et al）.基于层次分析和模糊综合评价法的配电网供电模式选型（A study of distribution network feeding modes selection based on analytic hierarchy process and fuzzy comprehensive evaluation）[J].电网技术（Power System Technology），2006，30（22）：67-71.

[9]周群艳，田澎，田志友（Zhou Qunyan，Tian Peng，Tian Zhiyou）.基于几何一致性指数的判断矩阵一致性改进（Consistency improvement of comparison matrix based on geometric consistency index）[J].西南交通大学学报（Journal of Southwest Jiaotong University），2006，41（2）：236-240.

[10]Tanaka H，Tsukao S，Yamashita D，et al.Multiple criteria assessment of substation conditions by pair-wise comparison of analytic hierarchy process[J].IEEE Trans on Power Delivery，2010，25（4）：3017-3023.

[11]张晓花，陈星莺，刘皓明，等（Zhang Xiaohua，Chen Xingying，Liu Haoming，et al）.一种新策略在电能质量综合评价中的应用（Application of a novel strategy in the comprehensive evaluation of power quality）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2008，20（6）：41-46.

[12]胡文锦，武志刚，张尧，等（Hu Wenjin，Wu Zhigang，Zhang Yao，et al）.风电场电能质量分析与评估（Analysis and evaluation on the electric power quality of the wind farm）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2009，21（4）：82-87.