基于产形齿条端面齿廓的相交轴渐开线变厚斜齿轮建模*

陈辰嘉，刘 文，林腾蛟，吕和生

(1.重庆大学 机械传动国家重点实验室，重庆 400044;2.重庆齿轮箱有限责任公司，重庆 402263)

1 引言

渐开线变厚齿轮在外形上沿轴线呈现一定的锥角，可广泛应用于平行轴、相交轴以及交错轴的空间传动中。变厚齿轮的主要特点是在不同的轴向截面上齿形具有不同的变位系数，通常沿轴向线性变化。

对于渐开线变厚齿轮，国内外学者做了较多的研究。Jesper Brauer针对直齿变厚齿轮从参数方程的角度分析了其几何特征［1］;林超、魏沛堂推导了变厚斜齿轮渐开线螺旋面、过渡曲面及齿根面齿面方程，建立了精确实体模型［2］;朱才朝、宋朝省等提出了变厚齿轮直接设计法和间接设计法，分析了设计参数对啮合主方向角的影响［3］，并研究了其啮合动态特性［4］，舒长生针对变厚斜齿轮轮齿左右两侧螺旋角的变化规律提出了附加螺旋角的概念［5］。研究人员在建立变厚斜齿轮齿面方程时都是从产形齿条法面方程着手进行推导，未能直接通过设定齿轮参数得到斜齿轮端面方程，建模过程相对繁琐。

笔者根据齿轮啮合原理，以产形齿条法面齿廓为基础，建立其端面齿廓方程，推导产形齿条与变厚齿轮间的坐标变换关系，求解两齿面相对滑移速度及产形齿条上的单位法矢构建啮合方程，得到渐开线变厚斜齿轮齿面表达式，而后利用UG软件建立相交轴渐开线变厚斜齿轮副的实体模型。

2 产形斜齿条端面方程的推导

在推导渐开线变厚斜齿轮齿面方程时，以假想产形齿条作为刀具加工变厚斜齿轮，产形齿条与被加工齿轮相对位置关系如图1所示。

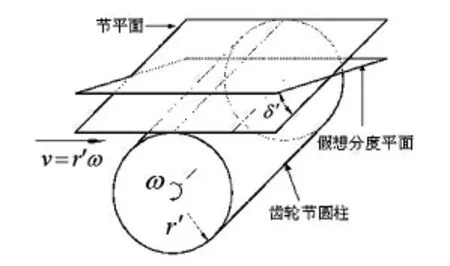
图1 产形齿条和齿坯相对位置关系

图1中，半径为r′的节圆柱与产形齿条节平面相切，节圆柱上的切点线速度r′ω等于齿条平移的速度，假想分度平面与节平面之间呈夹角δ'。

2.1 产形斜齿条法面方程

如图2所示，Sn(Xn，Yn，Zn)是空间固定坐标系，YnZn平面为产形齿条的分度平面，XnZn平面为产形齿条法向对称平面。在法向截面上，产形齿条的左侧齿廓分为AB和BC两部分，其中AB段为圆弧，包络出变厚齿轮齿根过渡曲线;BC段为直线，包络出变厚齿轮的渐开线齿面。

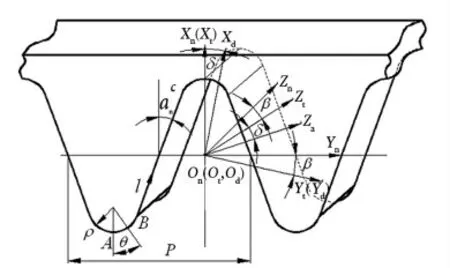
图2 产形齿条法向截面齿廓

BC上任一点在法向截面上方程为:

式中:Rzn为BC段中任意一点在坐标系Sn中的矢径;αn为法面压力角;mn为法面模数;h*an为齿顶高系数;l为BC中任意一点到点B的距离;下标n为刀具法面;–，+分别表示产形齿条左、右侧齿廓。

AB上任一点在法向截面上方程为:

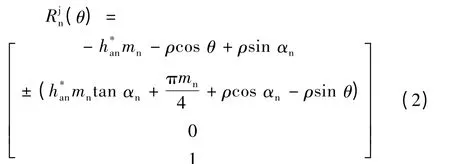
式中:Rjn为AB段中任意一点在坐标系Sn中的矢径;θ为圆弧上任一点与起始点A间的圆心角;ρ为产形齿条齿顶圆角半径。

2.2 产形斜齿条端面方程

将坐标系Sn绕Xn旋转β，得坐标系St(Xt，Yt，Zt)，再将坐标系St绕Yt旋转δ，得坐标系Sd(Xd，Yd，Zd)，如图2所示。

由式(1)、(2)可推导出产形齿条直线段和圆弧段在坐标系St中XtOtYt平面上的表达式如下。

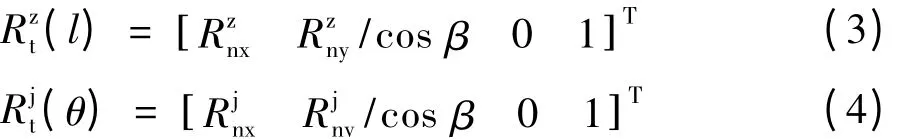
由式(3)、(4)可推导出产形齿条直线段和圆弧段在坐标系Sd中XdOdYd平面上的表达式如下。

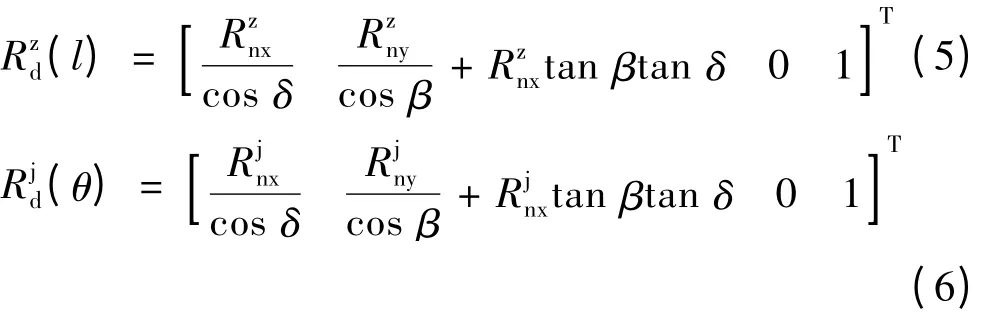
3 渐开线变厚齿轮齿面方程的推导

3.1 产形齿条的坐标变换

建立如图3所示的坐标系，Sd(Xd，Yd，Zd)坐标系与产形齿条固联，将坐标系Sd沿Zd负向移动距离u，然后绕Xd旋转β角得到坐标系Sp(Xp，Yp，Zp)，将坐标系Sp绕Yp旋转δ角得到坐标系Sc(Xc，Yc，Zc)。

图3 坐标系S d、S p、S c之间的位置关系

在坐标系Sc中，产形齿条齿面方程可通过如下坐标变换得到。

式中:Rc和Rd分别表示产形齿条齿面上各点在坐标系Sc和Sd下的矢径，Mpd为坐标系Sd到Sp的坐标变换矩阵，Mcp为坐标系Sp到Sc的坐标变换矩阵。

将式(5)、(6)、(8)代入式(7)，可得坐标系Sc下产形齿条直线段和圆弧段各点的矢径。

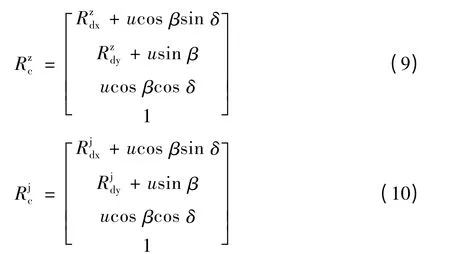
3.2 产形齿条齿面的单位法矢

坐标系Sc下产形齿条直线段(圆弧段)各点的位置表达式为l/u(θ/u)的函数，所以产形齿条齿面的单位法矢可以表示为下式。

3.3 啮合方程

产形齿条加工齿坯的过程，也是产形齿条齿面包络齿坯创成齿面的过程。图4所示为产形齿条与齿轮啮合时的相对位置关系。

图4 产形齿条与与齿轮啮合时相对位置关系

设Sb(Xb，Yb，Zb)为空间固定坐标系，Sj(Xj，Yj，Zj)为与被加工齿轮固联的坐标系。在初始位置，Sj与Sb重合，与产形齿条固联的坐标系Sc的原点Oc位于Xb轴上，与Ob的距离为r'。产形齿条1以线速度ω1r′向左移动，带动被加工齿轮2以角速度ω1绕Zj轴逆时针旋转。若产形齿条由初始位置向左移动r′φ1，则坐标系Sj绕Zj旋转角度φ1。

被加工齿轮绕Zj轴转速矢量可表示为:

设产形齿条上某点K的位置矢量为:

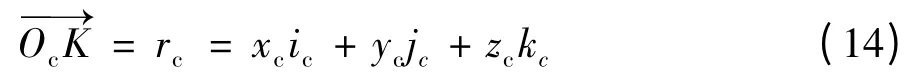
可得:

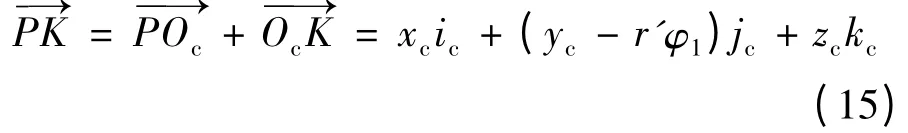
由式(13)、(15)可得，在K点处齿轮相对齿条的速度矢量为:

根据啮合原理，两齿面能在K点正确啮合的条件是K点的相对速度矢量垂直于过K点的两齿面的公法线矢量，即:

其中:nK表示刀具齿面单位法向矢量

将式(16)、(18)代入式(19)解得:

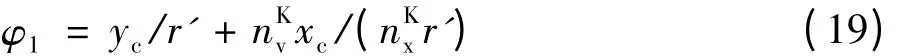
3.4 渐开线变厚齿轮齿面方程

将式(9)、(10)和(11)、(12)分别代入式(19)，解得产形齿条直线段和圆弧段的转角φ1。

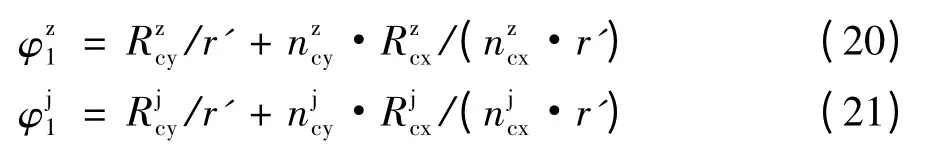
变厚齿轮齿面部分在Sj中的齿面方程为:

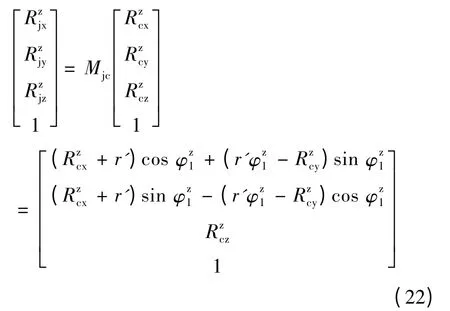
式中:Mjc为坐标系Sc到Sj的变换矩阵。

同理，变厚齿轮过渡圆弧在Sj中的参数方程为:

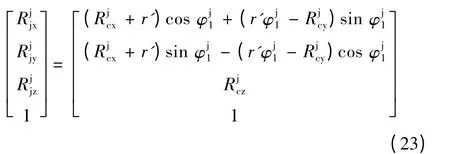
4 变厚斜齿轮副实体模型的建立

相交轴渐开线变厚斜齿轮副的参数如表1所列。

表1 渐开线变厚斜齿轮的参数

4.1 渐开线变原斜齿轮齿面点云生成［6-8］

以输入齿轮为例，在Matlab中根据变厚斜齿轮的齿面方程编写程序，可生成图5所示的齿面点云。图中5(a)为基于产形齿条端面齿廓方程得出的齿面点云，图5(b)为基于产形齿条法面齿廓方程得出的齿面点云。

两者对比分析可见，无论是从产形齿条端面方程还是法面方程出发，都能获得准确的齿面点云;不同的是图5(a)中每层点云都与齿轮端面平行，可通过设定齿轮大端和小端的变位系数，从而方便地建立满足齿宽要求的实体模型，而由图5(b)点云拟合得到曲面后，还需依据齿轮大、小端的变位系数计算轴向切面位置，通过曲面剪切形成变厚斜齿轮齿面，建模过程相对较为繁琐。

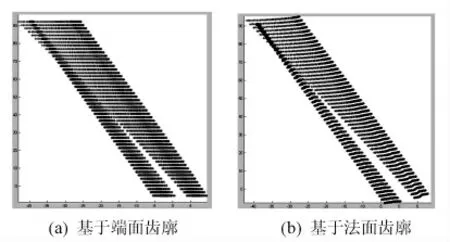
图5 输入轴渐开线变厚齿轮齿面点云

4.2 渐开线变厚斜齿轮建模及装配

相交轴渐开线变厚斜齿轮副的啮合模型，如图6所示。

交轴渐开线变厚斜齿轮副的啮合模型

将基于产形齿条端面齿廓方程得出的齿面点云输入Imageware拟合成变厚斜齿轮齿面，而后在UG中编辑曲面，通过缝合、阵列等操作得到变厚斜齿轮的实体模型。计算齿轮副装配位置，在UG中进行虚拟装配及干涉检验，即可得到图6所示的模型。

5 结论

采用空间啮合原理，基于产形齿条端面方程推导了渐开线变厚斜齿轮的齿面方程，建立了相交轴渐开线变厚斜齿轮副的装配模型，得出以下结论:①基于产形齿条法面齿廓的参数方程，经两次坐标变换可推导出包含螺旋角β和锥角δ两个基本参数的产形齿条端面方程;②从产形齿条端面齿廓方程入手，经坐标变换建立啮合方程，得出了渐开线变厚斜齿轮的齿面方程;③借助Matlab、Imageware、UG等软件建立了渐开线变厚斜齿轮副的实体模型和装配模型，结果显示该相交轴变厚斜齿轮副啮合状况良好。

［1］ Brauer J.Analytical Geometry of Straight Conical Involute Gears［J］.Mechanism and Machine Theory，2002，37(1):127-141.

［2］ 林 超，魏沛堂，朱才朝，等.变齿厚斜齿轮的齿面生成研究［J］.机械传动，2010，34(4):1-5.

［3］ 宋朝省，朱才朝，刘立斌，等.交错轴渐开线变厚齿轮传动节圆锥设计［J］.重庆大学学报，2012，35(8):48-53.

［4］ 宋朝省，朱才朝，Lim T C，等.小角度空间交错轴变厚齿轮传动啮合动态特性研究［J］.振动与冲击，2012，31(8):153-157.

［5］ 舒长生.变齿厚齿轮基圆螺旋角的计算［J］.传动技术，2001(3):5-9.

［6］ 沈永鹤，孙 融.变齿厚渐开线齿轮的应用和加工［J］.机械设计与研究，2003，19(3):83-84.

［7］ 李华敏，韩元莹，王知行.渐开线齿轮的几何原理与计算［M］.北京:机械工业出版社，1985.

［8］ 赵加元.渐开线齿轮轮齿的修形设计［J］.机械，2011(10):67-72.