二叉树上分枝马氏链的强大数定理

党慧,杨卫国,高荣,石志岩

(江苏大学理学院,江苏镇江 212013)

二叉树上分枝马氏链的强大数定理

党慧,杨卫国,高荣,石志岩

(江苏大学理学院,江苏镇江 212013)

首先给出了在可列状态空间取值的二叉树上分枝马氏链定义的离散形式,然后建立了二叉树上分枝马氏链的若干强极限定理,最后研究了二叉树上有限状态分枝马氏链的强大数定理.

二叉树;分枝马氏链;强极限定理;强大数定理

DO I：10.3969/j.issn.1008-5513.2013.05.0013

1 引言

树图T是一个没有回路的连通图,对于任意两个顶点σ/=t∈T,设σt是连接σ与t的唯一路径,路径σt中含有的边数记为d(σ,t),称为σ到t的距离.设T是一个以o为根顶点的局部有限的无限树图.对于T中的任意两个顶点σ,t,如果σ是处在从根顶点o到t的唯一路径上,则记为σ≤t.用σ∧t表示同时满足σ∧t≤t与σ∧t≤σ的离o最远的顶点.对于T上的任一顶点t,|t|表示o和t之间的距离.一个顶点如果其与根顶点的距离为n,则称该顶点位于第n层上.Ln表示T的第n层上所有顶点的子图,Lmn表示T的含有从n层到m层的所有顶点的子图,特别T(n)=Ln0表示T的含有从0层(根)到n层的所有顶点子图.如果树图T的根顶点有N个相邻顶点,而其他顶点有N+1个相邻顶点,称此树为Cayley树,记为TC,N.对于Cayley树TC,N上的每一个顶点t,在它的下一层都有N个相邻顶点,称这N个顶点为t的子代,t为这N个顶点的父代.本文主要研究二叉树TC,2(见图1),为了方便,将TC,2简记为T2.对于二叉树上任一顶点t,记t1,t2为t的两个子代.

设{Ω,F,P}为一概率空间,{Xt,t∈T2}为定义在{Ω,F,P}上的树指标随机过程,设A为T2的子图,记XA={Xt,t∈A},用|A|表示A中顶点的个数,xA表示XA的实现.

树指标随机过程是近年来发展起来的概率论的一个新的研究方向.文献[1]给出了树指标马氏链的定义并研究其常返性及角常返性.文献[2]研究了齐次树上某些平稳随机场的熵率.文献[3]研究了齐次树指标有限状态马氏链的强大数定理和渐近均分性(AEP).文献[4]研究了齐次树指标层非齐次马氏链的强大数定理和渐近均分性(AEP).文献[5]研究了一致有界树指标马氏链的强大数定理和渐近均分性(AEP).文献[6]研究了Cayley树指标有限状态非齐次马氏链的强大数定理和渐近均分性(AEP).文献[7]研究了Cayley树指标非对称马氏链的强大数定理和渐近均分性.文献[8]定义了在任意状态空间取值的二叉树上分枝马氏链,并研究了其极限定理.

图1 二叉树TC,2

本文首先给出在可列状态空间取值的二叉树上分枝马氏链定义的离散形式,然后研究二叉树上有限状态分枝马氏链的强大数定理.在文献[8]中研究的强大数定理要求随机变量是同分布的,并不做此要求,而且与文献[8]不同的是,本文采用的是与文献[7]类似的方法,即通过构造一个非负鞅先建立二叉树上分枝马氏链的强极限定理,然后利用这个强极限定理证明本文的强大数定理.

2 定义

3 强极限定理

4 强大数定理

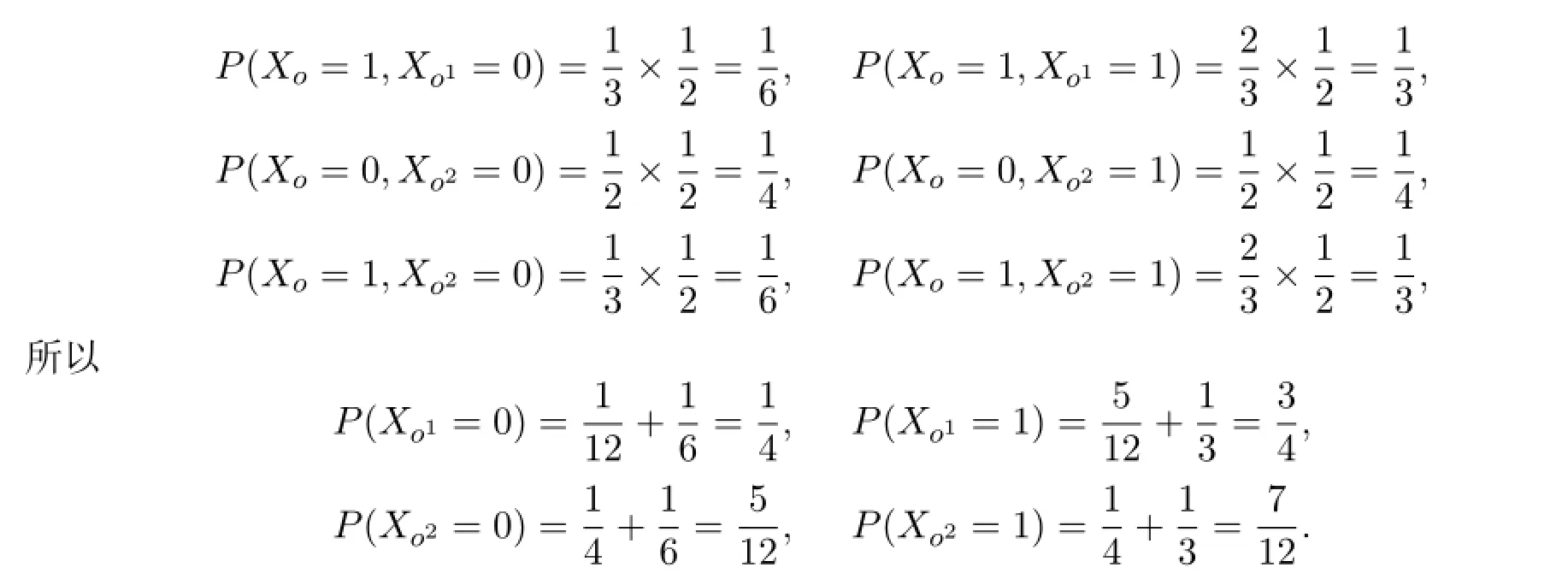
[1]Ben jam ini I,Peres Y.M arkov chains indexed by trees[J].Ann.Probab.,1994,22:219-243.

[2]Berger T,Ye Z.Entropic aspects of random f elds on trees[J].IEEE Trans.Inform.Theory,1990,36:1006-1018.

[3]Yang W G.Som e lim it properties for M arkov chains indexed by a hom ogeneous tree[J].Statist.P rob.Lett., 2003,65:241-250.

[4]Yang W G,Ye Z.The asym p totic equipartition property for nonhomogeneous M arkov chains indexed by a homogeneous tree[J].IEEE Trans.In form.Theory,2007,53:3275-3280.

[5]Huang H L,Yang W G.Strong law of large num bers for M arkov chains indexed by an in fnite tree w ith uniform ly bounded degree[J].Sci.China Ser.A,2008,51:195-202.

[6]Dong Y,Yang W G,Bai J F.The strong law of large numbers and the Shannon-M cM illan theorem for nonhom ogeneous M arkov chains indexed by a Cay ley tree[J].Statist.Probab.Lett.,2011,81:1883-1890.

[7]Dong Y,YangW G.Strong law of large numbers and asym ptotic equipartition probability for nonsymmetric M arkov chain indexed by Cayley tree[J].M athematical Research Exposition,2010,30(6):976-984.

[8]Guyon J.Lim it theorem s for bifurcating M arkov chains.App lication to the detection of cellular aging[J]. Ann.App l.Probab.,2007,17:1538-1569.

Strong law of large num bers for bifu rcating M arkov chains
indexed by a binary tree

Dang Hui,Yang Weiguo,Gao Rong,Shi Zhiyan

(Faculty of Science,Jiangsu University,Zhen jiang 212013,China)

In this paper,we f rst introduce the def nition of the discrete form of bifurcating M arkov chains indexed by a binary tree,then obtain some strong lim it theorem s for bifurcating M arkov chains indexed by a binary tree,and f nally,we obtain the strong law of large numbers for binary tree-indexed bifurcating Markov chainsw ith f nite state space.

binary tree,bifu rcating M arkov chains,strong lim it theorem s,strong law of large numbers

O211. 4;O211.6

A

1008-5513(2013)05-0529-07

2013-04-012.

国家自然科学基金(11071104);江苏大学大学生科研立项(12A 409).作

者简介：党慧(1987-),在读硕士,研究方向:概率极限理论.

2010 MSC:60J10,60F15