多复变数星形映射在某方向上精确的偏差定理
2013-06-27卢金刘太顺王俊
卢金,刘太顺,王俊
(湖州师范学院数学系,浙江湖州 313000)
多复变数星形映射在某方向上精确的偏差定理
卢金,刘太顺,王俊
(湖州师范学院数学系,浙江湖州 313000)
研究了Cn中单位多圆柱上星形映射在某方向上精确的偏差定理.给出了
复Banach空间单位球的某方向上精确的偏差的上界,同时给出了下界的猜测.
星形映射;偏差定理;增长定理
1 引言
平面单位圆盘上的单叶函数的偏差定理是1907年由Kobe给出的,它对单位圆盘上的单叶函数f明确的给出了用|z|来表达|f′(z)|的上下确界的公式.单位圆盘上的正规化双全纯星形函数有完整的偏差定理.

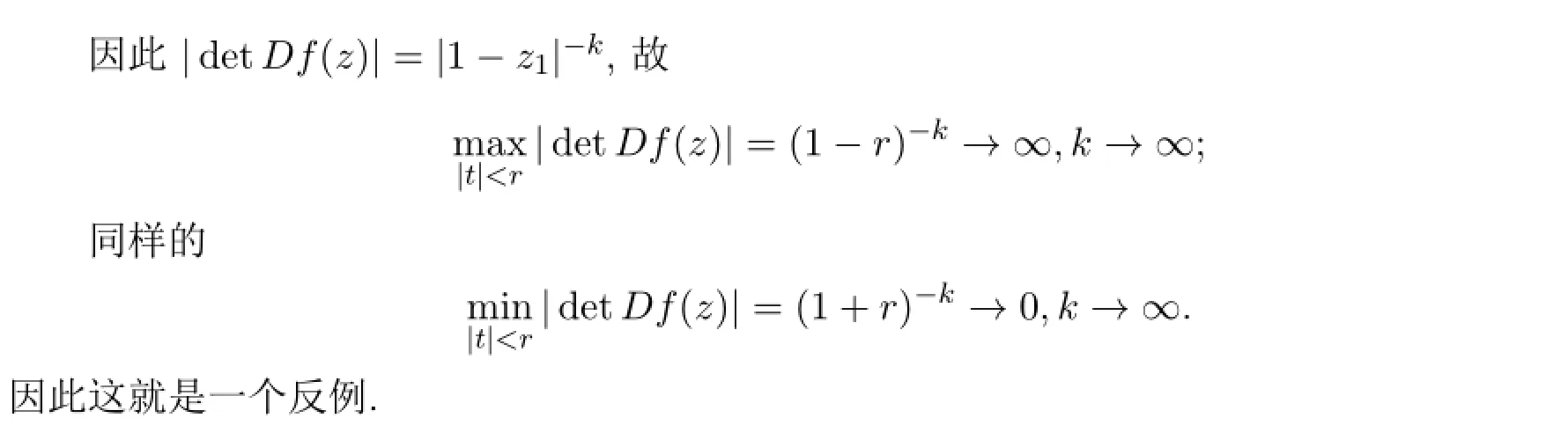
单复变数推广到多复变数中,对|f′(z)|的有很多不同推广,例如文献[3].而最先在多复变数中给出|det D f(z)|的估计是文献[4],给出C2上的正规化双全纯凸映射的偏差定理.然后,文献[5]对单位球Bn上正规化双全纯凸映射建立了矩阵形式偏差定理,1999年,文献[6]将该结果推广到Cn中一般的有界凸圆形域Ω上.2003年文献[7]又将该结果推广到复Banach空间单位球上,给出了下面形式的偏差定理:
定理1.2设B为Banach空间单位球,若f是B上的正规化双全纯凸映射,则∀z∈B, ξ∈X,有

其中FBC(x,ζ)是B上的Carath´eodory度量的无穷小形式,FBK(x,ζ)是B上的Kobayashi度量的无穷小形式.
在单复变数中,若考虑零点的阶数,文献[8]于1996年首先建立了单位圆盘D上的正规化双全纯凸函数f(其中z=0是f(z)-z的k+1阶零点)精确的增长、掩盖定理及偏差定理,同时利用著名的A lexander定理得到了单位圆盘D上的正规化双全纯星形函数f(其中z=0是f(z)-z的k+1阶零点)精确的增长、掩盖定理.多复变数中,文献[4]则最先给出Cn中单位球Bn上正规化双全纯k次对称星形映射精确的增长、掩盖定理.2002年,文献[9]又在复Banach空间中单位球上的得到了正规化双全纯k次对称凸映射精细(但不精确)的增长、掩盖定理.如果在多复变数中引入k阶零点的概念,那么容易知道:若f是正规化k次对称映射,则x=0是f(x)-x的k+1阶零点.反之,却不一定成立.一个十分自然的想法是:在多复变数中若考虑零点的阶数(即x=0是f(x)-x的k+1阶零点),是否有类似单复变数情形的结论?2004年,文献[10]在复Banach空间单位球上星形映射精确的增长、掩盖定理.
星形映射是多复变几何函数论研究的重要内容,文献[11]中给出了星形映射的偏差定理.本文研究了单位多圆柱上星形映射在某个方向上精确的偏差定理.给出了复Banach空间单位球的某方向上精确的偏差的上界,同时给出了下界的猜测.
2 预备知识


3 主要结果


4 猜想

[1]Duren P L.Univalent Function[M].Berlin:Sp ringer-Verlag,1983.
[2]龚昇.多复变数的凸映照和星形映照[M].2版.北京:科学出版社,2003.
[3]殷承元.多复变数的二阶微分从属[J].纯粹数学与应用数学,2003,19(1):83-87.
[4]Barnard RW,FitzGeral C H,Gong S.A distortion theorem for biholomorphicmappings in C2[J].Trans. Amer.Math.Soc.,1994,344:902-924.
[5]Gong S,W ang SK,Yu Q H.Biholom orphic convex m app ings of ball in C2[J].Pacif c J.M ath.,1993,161(2): 287-306.
[6]Gong S,Liu T S.Distortion theorem s for biholomorphic convex mappings on bounded convex circu lar domains[J].Chin.Ann.of M ath.,1999,20B(3):297-304.
[7]Liu T S,Zhang W J.A distortion theorem of biholom orphic convex m app ings in a Banach space[J].Acta. M ath.Sinica.,2003,46A(6):1041-1046.
[8]Graham I,Varolin D.B loch constants in one and several variab les[J].Pacif c J.M ath.,1996,174:347-357.
[9]T Honda.The grow th theorem for k-fold symm etric convex m appings[J].Bu ll London M ath.Soc., 2002,34:717-724.
[10]Liu T S,Liu X S.On the p recise grow th,covering,and distortion theorem s for normalized biholomorphic mappings[J].J.Math.Anal.appl.,2004,295:404-417.
[11]Liu T S,W ang JF,Lu J.D istortion theorem sof starlikem app ingsalong a unit direction in Cn[J].Taiwanese J.Math.,2011,15(6):2601-2608.
On the p recise d istortion theorem s for star like m ap p ings along a unit d irection in several com p lex variab les
Lu Jin,Liu Taishun,Wang Jun
(Department of M athematics,Huzhou Teachers College,Huzhou 313000,China)
We estab lished the precise distortion theorem s of Jacobianmatrix for starlikemappings along a unit direction on the unit polydisc of Cn.We obtained the upper bound estimate of the p recise distortion theorem for starlikemappings on the unit ball of a com p lex Banach space.Finally,a conjectures of the lower bound was considered.
starlikem appings,d istortion theorem s,grow th theorem s
O174.56
A
1008-5513(2013)05-0507-06 DO I:10.3969/j.issn.1008-5513.2013.05.010
2012-03-30.
国家自然科学基金(11101139,11261022,11031008);浙江省新苗计划;湖师院科研项目(KX 21057).
卢金(1981-),博士,讲师,研究方向:多复变几何函数论.
2010 MSC:32A 30,32H 02
