基于多分类相关向量机的变压器故障诊断新方法

尹金良，朱永利，俞国勤

（1.华北电力大学电气与电子工程学院，河北 保定 071003；2.上海电力公司，上海 200025）

0 引言

电力变压器是电力系统的重要设备，其运行状态直接影响系统的安全水平[1-3]，及时发现变压器潜伏性故障，可以防止由此引发重大事故。

由于变压器油中溶解气体的含量与比值可以在很大程度上反映变压器的运行状态[4-8]，基于此已形成了IEC推荐的三比值法、Rogers法等传统方法，以及贝叶斯网络(BN)、支持向量机(SVM)等人工智能方法[4-8]。然而在现场运行中发现传统算法存在缺编码、编码界限过于绝对等主要缺陷[2,5]；BN处理不确定性问题能力强，但需要大量样本数据且计算量大[9]；SVM需要训练样本数据少，泛化能力强，但存在规则化系数确定困难、核函数必须满足Mercer条件等固有局限[10-17]。

多分类相关向量机(Multiclass Relevance Vector Machine，M-RVM)是Damoulasy等人于2008年提出的一种基于贝叶斯框架的统计学习算法[18-19]。M-RVM具有BN和SVM的上述优点，同时克服了二者的缺陷。M-RVM 模型基函数权值只有少数非零，相关向量数量少，模型稀疏度高，计算复杂度低；可以直接实现多分类；更重要的是M-RVM可以输出各类别成员概率，输出具有概率统计意义，便于分析不确定性问题[18-19]。

M-RVM 尚未应用于变压器故障诊断。鉴于变压器故障样本数据少，故障不确定性因素多，故障诊断本质为多分类问题以及M-RVM上述优点，提出了基于M-RVM的变压器故障诊断方法，以克服BN诊断方法需要大量样本数据且计算量大，SVM诊断方法规则化系数确定困难等问题。本文给出了该方法的具体实现和诊断过程，并通过实例验证了该方法的有效性。

1 多分类相关向量机介绍

1.1 M-RVM模型简介

M-RVM 采用分层贝叶斯模型结构，通过引入多项概率似然函数(Multinomial Probit Likelihood)，实现了多分类和输出类别成员概率。

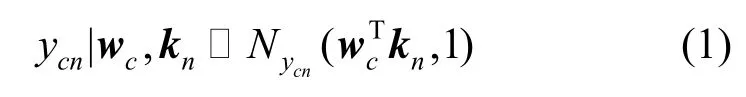
引入多项概率联系函数如式(2)，将回归目标转化为类别标签。

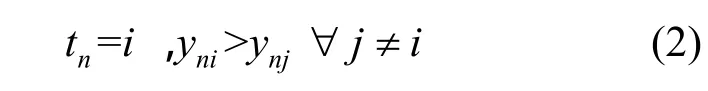
由此产生的多项概率似然函数[21-22]如式(3)，其中 uN(0,1)。

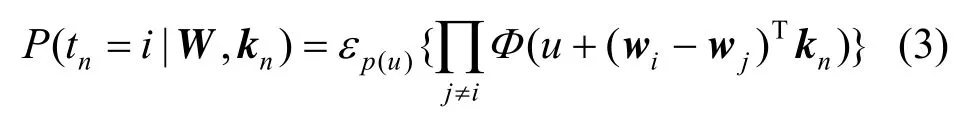
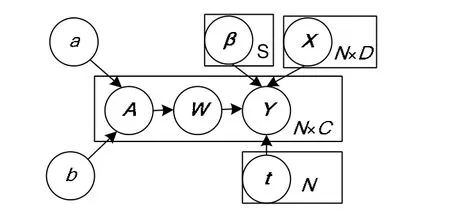
图1 分层贝叶斯模型Fig. 1 Hierarchical Bayesian model

根据图1可以推导出后验概率，其中cA为由A的c列导出的对角阵。

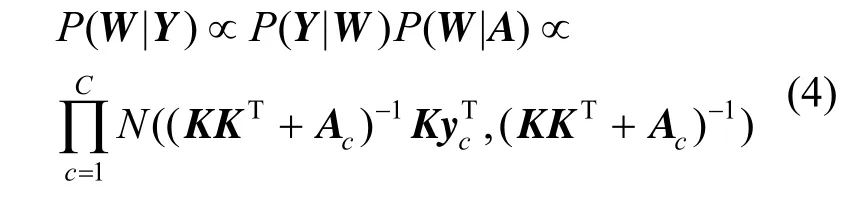
由最大后验概率估计的方法可得

因此给定类别时权重的基于最大后验(MAP)的更新方法如式(6)。

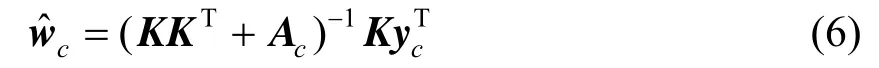
根据式(6)以及文献[23]，可以推导辅助变量的E-step形式，对于i类如式(7)，对于" c≠i如式(8)。

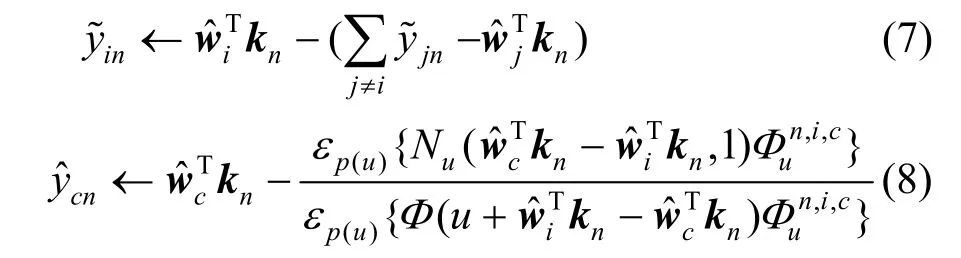
权重向量先验参数的后验概率分布如式(9)。

Gamma分布的均值为

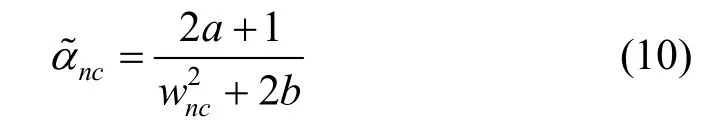
1.2 M-RVM模型学习

本文M-RVM模型学习采用按照贡献标准逐步加入样本的构造方法，该方法采用了快速type-II 最大似然(Fast Type-II ML)和最大期望(EM)参数更新方法[19]。

由log边缘似然函数可以推导出式(11)，其中

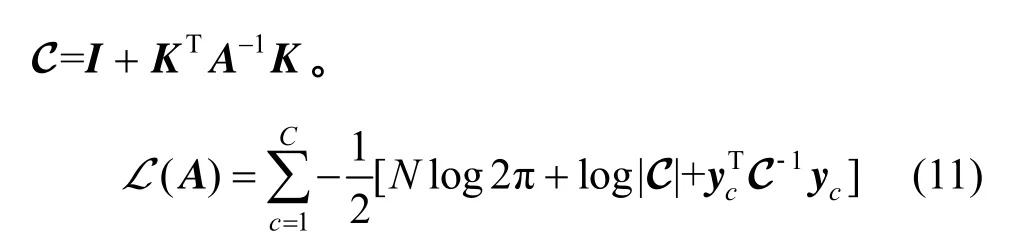
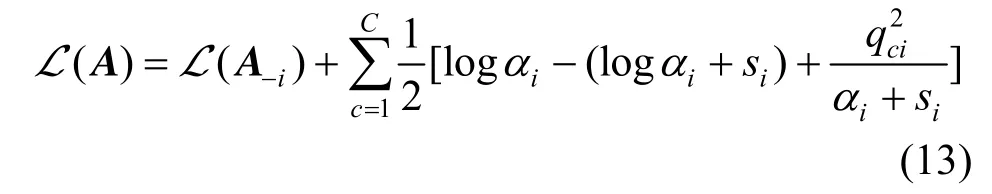
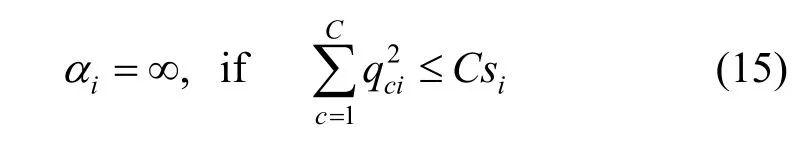
为了便于描述第i个样本对模型的信息贡献量定义 θi。

设迭代过程中有活动集A，活动集样本数为M，在模型学习的过程中，式(6)修正为式(17) ，其中

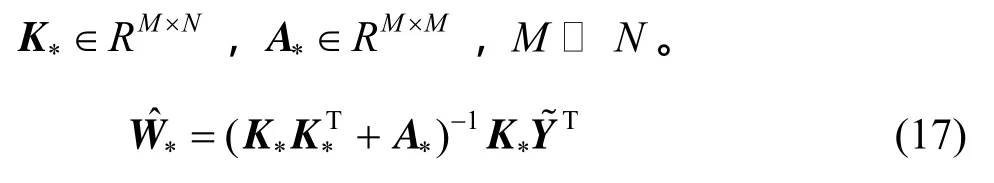
文献[19]给出了ia的初始化公式如式(18)所示，以及样本选择方法和收敛标准，本文收敛标准选用conv1。

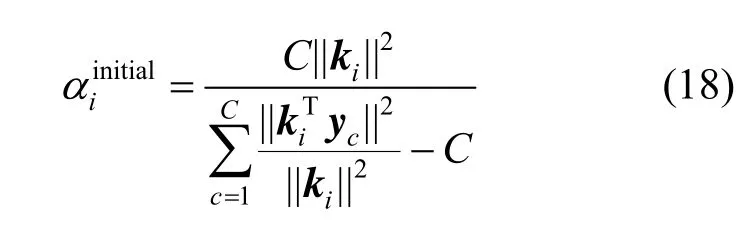
2 基于M-RVM的变压器故障诊断

2.1 选取输入向量

可反映变压器内部故障且大部分在线监测装置能监测到的特征气体主要有H2、CH4、C2H6、C2H4、C2H2五种。本文选取 H2占总气体含量的比值，记为x1，CH4、C2H6、C2H4、C2H2占总烃量的比值，分别记为x2, x3, x4, x5，作为特征输入变量，输入向量的模式为：[x1, x2, x3, x4, x5]。

2.2 确定变压器故障类型的划分及其表示方法

变压器故障诊断本质上是一个多分类问题，由于受可获得样本数据的限制，本文将变压器状态分为正常(N)、低能放电(D1)、高能放电(D2)、中低温过热(T12)、高温过热(T3)、局部放电(PD)六种状态。并分别采用向量[0,0,0,0,0,1]T、[0,0,0,0,1,0]T、[0,0,0,1,0,0]T、[0,0,1,0,0,0]T、[0,1,0,0,0,0]T、[1,0,0,0,0,0]T表示。如果有足够的复故障样本数据，可将变压器状态进一步划分为复故障状态或再细分。

2.3 基于M-RVM的变压器故障诊断的输出向量

M-RVM可以直接实现多分类和输出变压器为各种状态的概率，故障诊断的输出向量模式为：[pPD,pT3, pT12, pD2, pD1, pN]，pPD、pT3、pT12、pD2、pD1、pN分别代表变压器的状态为PD、T3、T12、D2、D1、N的概率，记输出向量的索引集为I={ PD, T3, T12,D2, D1, N }。诊断结果为变压器各种状态中概率最大的状态，即

2.4 选取核函数

常见的核函数有：线性核函数，多项式核函数和径向基核函数(RBF)。本文M-RVM采用变压器故障诊断中通常采用的 RBF核函数，RBF核函数如式(20)所示，其中s为核函数的高宽参数。

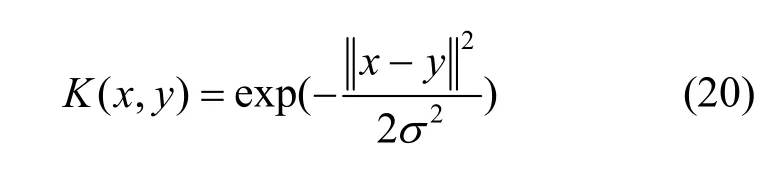
2.5 基于M-RVM的变压器故障诊断过程

基于M-RVM的变压器故障诊断具体诊断过程如下，故障诊断流程如图2所示。

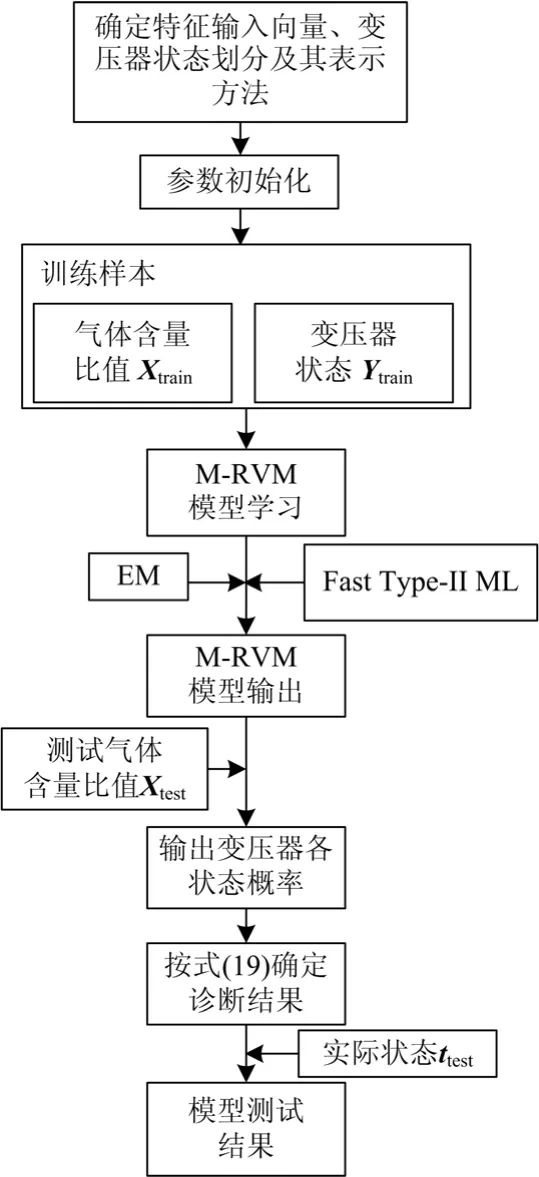
图2 基于M-RVM的变压器故障诊断流程图Fig. 2 Flow chart of transformer fault diagnosis based on M-RVM

(1) 依据可以获取的变压器数据类型选取特征输入向量。

(2) 依据研究问题的特点，划分变压器的状态，并确定各种状态相应的表示方法。

(3) 选取样本数据[X,t]。

(4) 选取核函数，按1/D确定核函数参数[19]。

算法1

(2) 引入一个训练样本数据，按式(18)初始化M-RVM模型；

(3) while 不满足收敛条件 do

(4) if θi>0 and αi<∞ then

(5) 按式(14)更新αi(样本已在模型)

(6) else if θi>0 and αi=∞ then

(7) 按式(14)设置αi(新添加到模型的样本)

(8) else if θi≤0 and αi<∞ then

(9) 设置αi=∞(从模型中删除样本)

(10) end if

(12) M-Step求Y:(7)，(8)

(13) 重新计算θi" iÎ{1,…,N}

(14) if 对于jÏA $ θj>0 then

(15) 寻找 jÏA 使 θj>θn" nÏA

(16) else if 对于jÎA $ θj<0 then

(17) 寻找 jÎA 使 θj<θn" nÎA

(18) else

(19) 随机从A中选取一个样本赋给j

(20) end if

(21) Set i=j

(22) end while

(23) 输出基于M-RVM的变压器故障诊断模型；

(24) 输入测试数据testX ；

(25) 按式(19)确定变压器的诊断结果，与变压器的实际状态testt 进行比较。

3 实例分析

本文选用由河北省衡水市和上海市供电公司提供以及从相关文献下载的变压器DGA数据共355组进行验证。为了验证本文所提方法的有效性，分别采用BN、SVM和M-RVM方法进行变压器故障诊断实例验证。

SVM 核函数选用 RBF，采用“一对一”的分类方法，应用网格搜索与10折交叉验证相结合的方法优化规则化系数和核函数参数；BN采用朴素贝叶斯网络分类器；M-RVM采用快速type-II 最大似然(Fast Type-II ML)和最大期望估计(EM)的方法进行模型推断，具体实现过程如2.5节所述。BN、SVM、M-RVM方法均按2.1节确定输入向量。

笔者经过大量的试验表明，在其他条件相同的情况下：

(1)与核函数选用线性核函数和多项式核函数相比，M-RVM核函数选用RBF时变压器故障诊断正确率比较高。本文核函数选用RBF。

(2) M-RVM诊断方法的诊断速度足以满足工程需求。本文对210个测试样本进行了100次试验，平均用时0.127 9 s。

图3给出变压器故障诊断采用M-RVM方法时，相关向量的数量在模型学习迭代过程中的变化情况。由图3可以看出M-RVM模型最终只需要少量的相关向量，模型稀疏度高，模型确定后，输入新的样本数据进行诊断时，计算复杂度低。

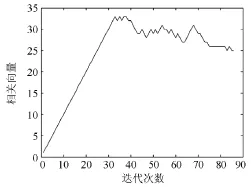
图3 相关向量在模型学习迭代过程中的变化情况Fig. 3 Changes of the number of relevance vector during the iteration process of model learning

表1给出采用BN、SVM、 M-RVM方法的故障诊断结果。

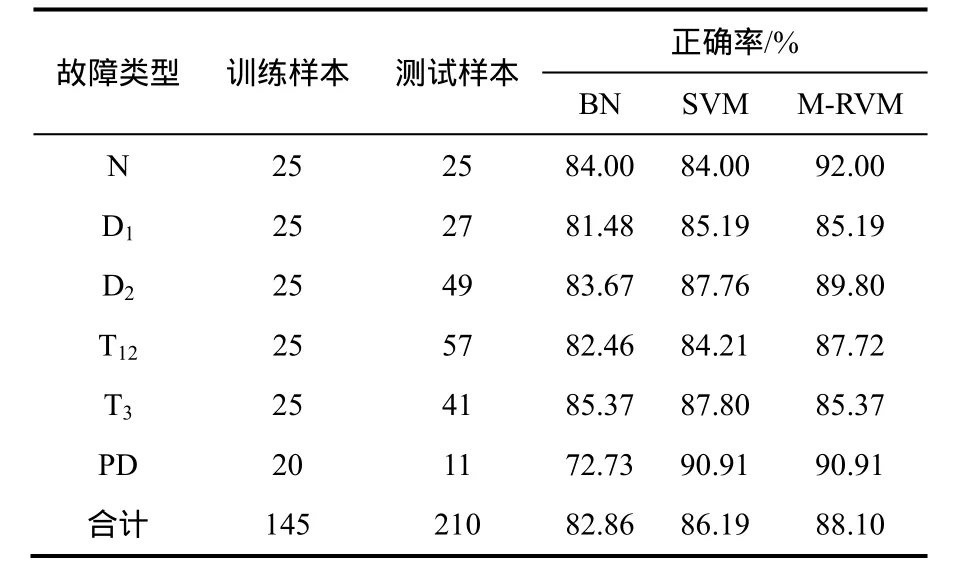
表1 BN、SVM、M-RVM方法的变压器故障诊断正确率Table 1 Comparison of fault diagnosis results among BN, SVM and M-RVM methods

表2列出了不同方法的6组变压器故障诊断的典型实例。

对应于表 2中 6组变压器故障诊断实例，M-RVM输入如式(21)X所示，M-RVM的输出如式(22)P所示。P中的行向量代表以与之相对应的X中的行向量为输入时，变压器的状态为PD、T3、T12、D2、D1、N的概率，按式(19)可得表2给出的M-RVM方法的诊断结果t=[N D1D2T12T3PD]T。

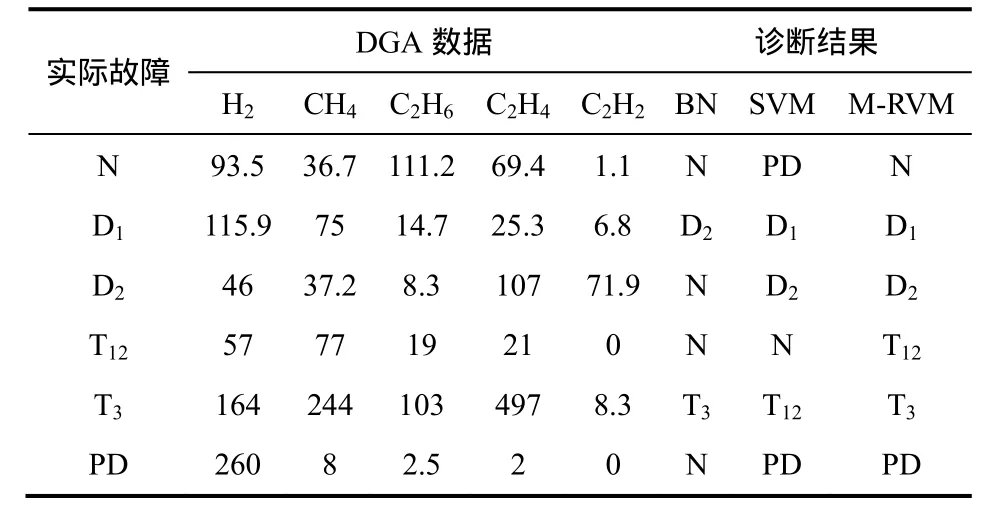
表2 变压器故障诊断实例Table 2 Cases of fault diagnosis for power transformer

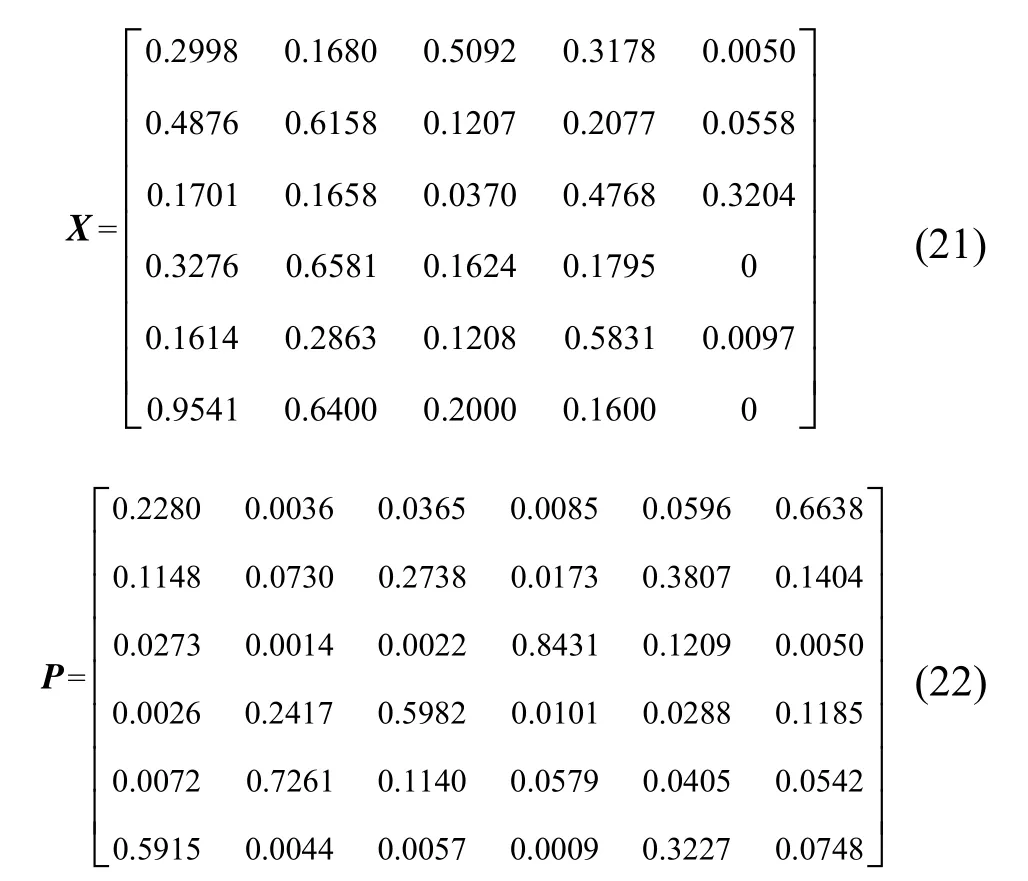
由表1和表2分析可知，与基于BN、SVM的变压器故障诊断方法相比，本文所提方法具有较好的故障诊断效果。由M-RVM的输出结果分析可知，本文所提方法可以输出变压器各种状态的概率，可以为变压器的检修提供更多的可用信息。

4 结论

鉴于变压器故障样本数据少，故障不确定性因素多，故障诊断本质为多分类问题，提出了基于M-RVM的变压器故障诊断方法，以克服BN诊断方法需要大量样本数据且计算量大，SVM诊断方法确定规则化系数困难等问题。该方法可以直接实现多分类，模型输出具有概率统计意义；模型只需少量的相关向量，稀疏度高，故障诊断时计算复杂度低。本文给出了该方法的具体实现方法和诊断过程，通过实例验证了同基于BN、SVM的诊断方法相比，M-RVM故障诊断方法具有较好的诊断效果。

[1] 任静, 黄家栋. 基于免疫 RBF神经网络的变压器故障诊断[J]. 电力系统保护与控制, 2010, 38(11): 6-9.REN Jing, HUANG Jia-dong. Transformer fault diagnosis based on immune RBF neural network[J].Power System Protection and Control, 2010, 38(11): 6-9.

[2] 李中, 苑津莎, 张利伟. 基于自组织抗体网络的电力变压器故障诊断[J]. 电工技术学报, 2010, 25(10):200-206.LI Zhong, YUAN Jin-sha, ZHANG Li-wei. Fault diagnosis for power transformer based on the self-organization antibody net[J]. Transactions of China Electrotechnical Society, 2010, 25(10): 200-206.

[3] 刘丽, 唐杰, 刘卓. 基于改进微分进化优化神经网络的电[J]. 电力系统保护与控制, 2010, 38(20): 106-109.LIU Li, TANG Jie, LIU Zhuo. Fault diagnosis of power transformer based on improved differential evolution-neural network[J]. Power System Protection and Control, 2010, 38(20): 106-109.

[4] Tang W H, Wu Q H. Condition monitoring and assessment of power transformers using computational intelligence[M]. New York: Springer-Verlag Press, 2011:95-104.

[5] 张德明. 变压器分接开关状态监测与故障诊断[M]. 北京: 中国电力出版社, 2008: 121-142.

[6] 贾嵘, 张云, 洪刚. 基于改进PSO的LSSVM参数优化在变压器故障诊断中的应用[J]. 电力系统保护与控制,2010，38(17): 121-124.JIA Rong, ZHANG Yun, HONG Gang. Parameter optimization of least squares support vector machine based on improved particle swarm optimization in fault diagnosis of transformer[J]. Power System Protection and Control, 2010, 38(17): 121-124.

[7] FEI Sheng-wei, ZHANG Xiao-bin. Fault diagnosis of power transformer based on support vector machine with genetic algorithm[J]. Expert Systems with Applications,2009, 36(8): 11352-11357.

[8] 董明, 孟源源, 徐长响, 等. 基于支持向量机及油中溶解气体分析的大型电力变压器故障诊断模型研究[J].中国电机工程学报, 2003, 23(7): 88-92.DONG Ming, MENG Yuan-yuan, XU Chang-xiang, et al.Fault diagnosis model for power transformer based on support vector machine and dissolved gas analysis[J].Proceedings of the CSEE, 2003, 23(7): 88-92.

[9] 孙即祥. 现代模式识别[M]. 北京: 高等教育出版社,2008: 454-494.

[10] Tipping M E. The relevance vector machine[J]. Advances in Neural Information Processing Systems, 2001, 12:652-658.

[11] Bishop C M, Tipping M E. Variational relevance vector machines[C] // Proceedings of the 16th Conference on Uncertainty in Artificial Intelligence, Morgan Kaufmann,2000: 46-53.

[12] Tipping M E. Sparse Bayesian learning and the relevance vector machine[J]. Journal of Machine Learning Research, 2001, 1: 211-244.

[13] 何创新, 李彦明, 刘成良, 等. 基于滑动平均与相关向量机的齿轮早期故障智能诊断[J]. 振动与冲击, 2010,29(12): 89-92.HE Chuang-xin, LI Yan-ming, LIU Cheng-liang, et al.Incipient fault diagnosis based on moving average and relevance vector machine[J]. Journal of Vibration and Shock, 2010, 29(12): 89-92.

[14] 杨成福, 章毅. 相关向量机及在说话人识别应用中的研究电子[J]. 电子科技大学学报, 2010, 39(2): 311-315.YANG Cheng-fu, ZHANG Yi. Study to speaker recognition using RVM[J]. Journal of University of Electronic Science and Technology of China, 2010, 39(2):311-315.

[15] 陶新民, 徐晶, 杜宝祥, 等. 基于相空间 RVM 的轴承故障检测方法[J]. 振动与冲击, 2008, 27(10): 6-10.TAO Xin-min, XU Jing, DU Bao-xiang, et al. Bearing fault detection based on RVM using phase space[J].Journal of Vibration and Shock, 2008, 27(10): 6-10.

[16] Demir B, Erturk S. Hyperspectral image classification using relevance vector machines[J]. IEEE Geoscience and Remote Sensing Letters, 2007, 4(4): 586-590.

[17] Gholami B, Haddad W M, Tannenbaum A R. Relevance vector machine learning for neonate pain intensity assessment using digital imaging[J]. IEEE Trans on Biomedical Engineering, 2010, 57(6): 1457-1466.

[18] Damoulas T, Ying Y, Girolami M A, et al. Inferring sparse kernel combinations and relevance vectors: an application to subcellular localization of proteins[C] //Proceedings of the 7th International Conference on Machine Learning and Applications (ICMLA2008),San Diego, USA, 2008.

[19] Psorakis I, Damoulas T, Girolami M A. Multiclass relevance vector machines: sparsity and accuracy[J].IEEE Trans on Neural Networks, 2010, 21(10):1588-1598.

[20] Girolami M, Rogers S. Hierarchic Bayesian models for kernel learning[C] // Proceedings of the 22nd International Conference on Machine Learning, Bonn,Germany, 2005: 241-248.

[21] Albert J, Chib S. Bayesian analysis of binary and polychotomous response data[J]. Journal of the American Statistical Association, 1993, 88: 669-679.

[22] Damoulas T, Girolami M A. Probabilistic multi-class multi-kernel learning: on protein fold recognition and remote homology detection[J]. Bioinformatics, 2008,24(10): 1264-1270.

[23] Damoulas T, Girolami M A. Combining feature spaces for classification[J]. Pattern Recognition, 2009, 42(11):2671-2683.