裂隙岩体本构模型及数值模拟研究与应用
2013-06-26张兰翔查文华
张兰翔 查文华 王 昆
(安徽理工大学能源与安全学院)
裂隙岩体是含有众多节理裂隙的岩体介质,这些裂隙被称为岩体的初始损伤。在岩体的开挖过程中由于这些裂隙的存在而导致岩体的力学性质发生了变化[1-4]。为了反映裂隙岩体的力学性质的变化,本研究采用裂隙岩体损伤力学理论,在FLAC3D中建立裂隙岩体的损伤演化本构模型,根据FLAC3D提供程序二次开发接口,将自定义开发的本构模型应用于实际的工程中,得到较好的效果。
1 裂隙岩体弹塑性损伤演化本构模型
1.1 裂隙岩体初始损伤本构关系
裂隙岩体损伤的力学表现为损伤岩体的柔度或刚度发生了变化,对于有效应力张量,可以理解为使损伤岩体得到与损伤体在应力作用下相同的应变张量分量,即为Lematie应变等效原理。根据Betti能量互易定理以及压剪应力场中的裂隙扩展过程的能量转换与变化而得出的初始损伤本构关系如下[5]:
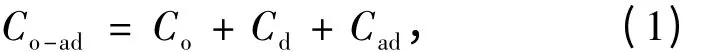
式中,Co-ad为裂隙岩体的柔度张量;Co为无损材料的柔度张量;Cd为由于裂隙存在而产生的附加柔度张量;Cad为裂隙扩展后产生的附加柔度张量。无损岩体的柔度张量Co的值为[6]
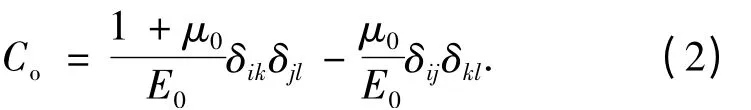
裂隙附加柔度张量Cd的值为[7]
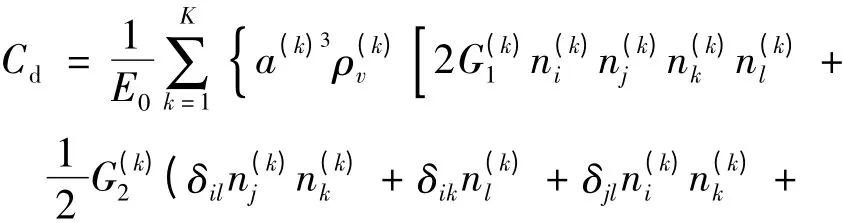

式中,E0为无损岩石材料弹性模量;μ0为无损岩石材料泊松比;a(k)为第k组面积;ρ(k)v为第k组裂隙密度;n(k)i、n(k)j、n(k)k和n(k)l均为第k组法线矢量分量;G1、G2是和裂隙形状及相互干扰有关的无量纲因子,
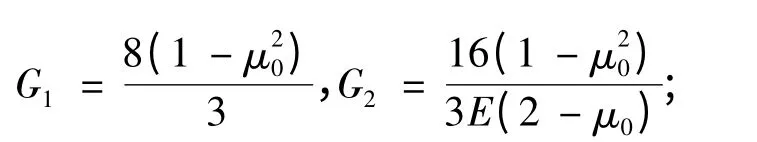
δij、δik、δjl、δkl、δjk为Kronecker符号,可以取值为1或0。
1.2 裂隙岩体损伤演化方程
1.2.1 压剪应力状态下裂隙岩体损伤柔度张量
按照能量可叠加原理,裂隙的损伤单元体扩展后系统内总等效变形能U可表示为[8]

式中,Ueo为裂隙岩体内裂隙未扩展前时应变能,Uad为单元体裂隙扩展后的变形能。裂隙岩体在压剪应力状态下裂隙扩展损伤带来的附加柔度张量[5]:
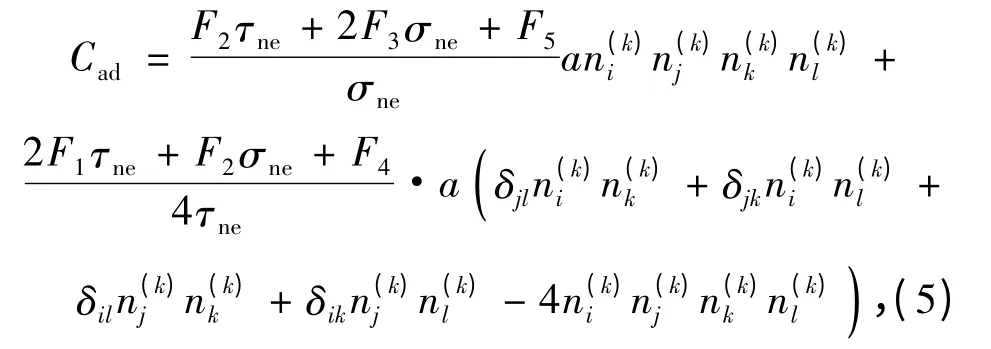
式中,

其中,a为裂隙半径;Fi(i=1,2,3,4,5)为系数;Cv,Cn为传剪、传压系数;σn为不连续面法向应力;ψ为内摩擦角。
根据Kemeny计算模型,分支裂隙的应力强度因子表示如下[9]:
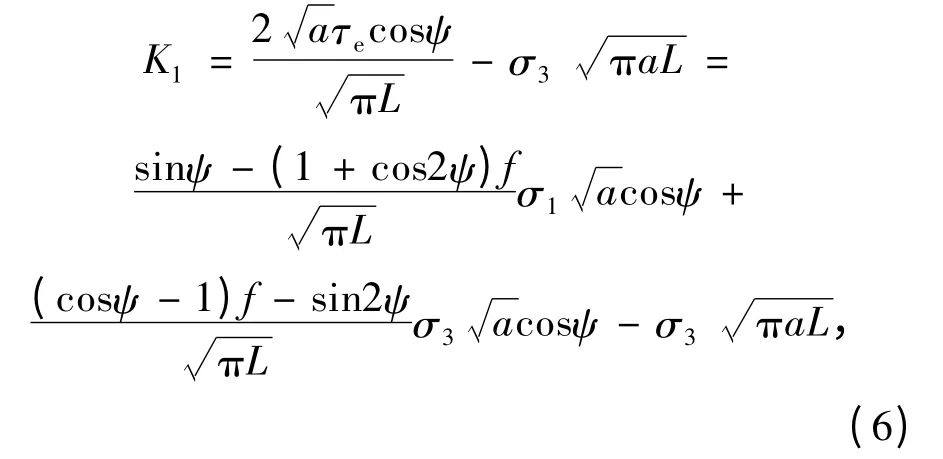
式中,L=l/a,l为扩展长度。当K1达到临界点时,裂隙的扩展就停止了;f为裂隙面摩擦因子。
1.2.2 拉剪应力状态下裂隙岩体损伤柔度张量
依据最大周向应力准则,当裂隙岩体等效Ι型应力强度因子达到断裂临界点时,裂隙就开始扩展。裂隙岩体在拉剪应力状态下裂隙扩展带来的附加损伤柔度张量为[5]

式中,pk为裂隙密度,E、μ为裂隙岩石的弹性模量、泊松比。
裂隙岩体在拉剪应力状态下,裂隙扩展后的应力强度因子为[9]
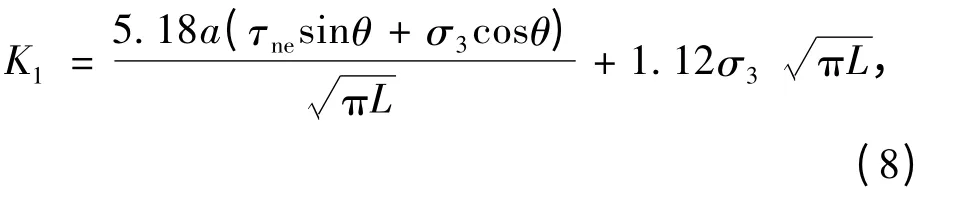
在拉应力的作用下,开裂角θ满足关系式为[5]
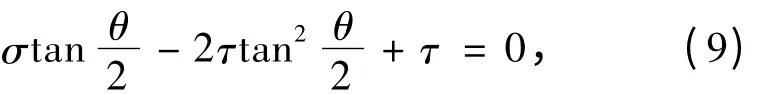
式中,θ为裂隙开裂角;τ为剪应力。
2 工程应用
2.1 工程概况及建模
某煤矿-480 m大巷水平距离为5 m,垂直距离为4 m的直壁半圆拱型巷道,该巷道水平层理,裂隙发育,围岩松软破碎,巷道顶板为泥质砂岩,底板为砂岩,其中裂隙面法向刚度Kn为1.8,裂隙面切向刚度Ks为0.54。根据该巷道的实际地质条件和其所处的空间位置关系,选择了模拟范围。该模拟区域沿X轴方向的长度为150 m,Y轴方向长70 m,Z轴方向长64 m,共划分56 852个单元格,63 418个节点。岩体物理力学参数见表l,建立开挖之后的FLAC3D模型见图1。
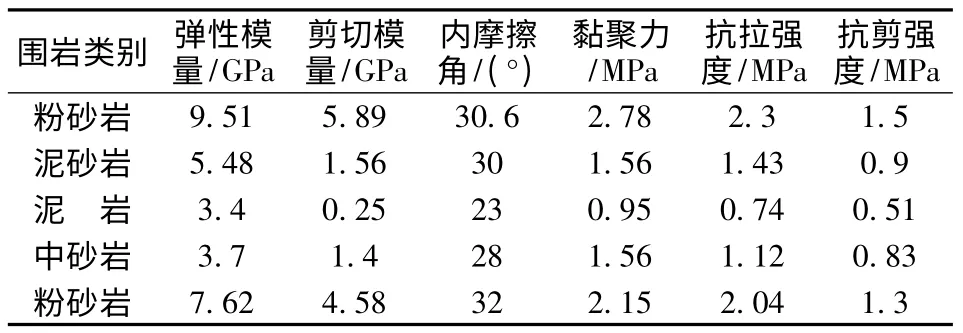
表1 围岩物理力学参数
2.2 计算结果分析
图1 数值分析模型
从图2中可以看出,2种模型条件下的破坏区分布规律基本相符,莫尔-库仑模型的破坏区略小于自定义裂隙岩体本构模型,2种模型所包含的弹塑性应力空间是一致的。总体上巷道塑性区主要集中在巷道帮部、底角及巷道的肩窝处。两帮塑性区范围大致在12 m左右,且巷道周边处围岩基本上都处于剪切破坏状态。

图2 巷道破坏区分布云图
基于2种模型的巷道垂直位移分布图和巷道水平位移分布图见图3和图4所示。2种模型计算的位移分布规律基本相似,在量值上莫尔-库仑模型略小,最大垂直位移都基本上在0.7 m范围左右,围岩最大水平位移为0.57 m。
由以上分析可知,采用自定义裂隙岩体本构模型得到的破坏区、位移分布规律与莫尔-库仑模型比较相符,量值上稍有差异,具体表现为自定义裂隙岩体本构模型的破坏区位移比莫尔-库仑模型大。
2.3 现场监测
为了探究该矿-480 m大巷裂隙岩体的实际变化情况,在大巷断面的顶部和水平两帮布设1组多点位移观测点,每隔10 m布设1个观测断面,共有6个观测断面,用于监测巷道顶底板和两帮的移近量。经过监测得到如图5和图6所示的移近量数据,可以看出,大巷顶底板最大移近量为0.1 m,大巷两帮最大移近量为0.08 m。可见本研究二次开发模型的计算结果与现场监测数据基本吻合,从而验证了程序的可行性。

图3 巷道垂直位移分布云图
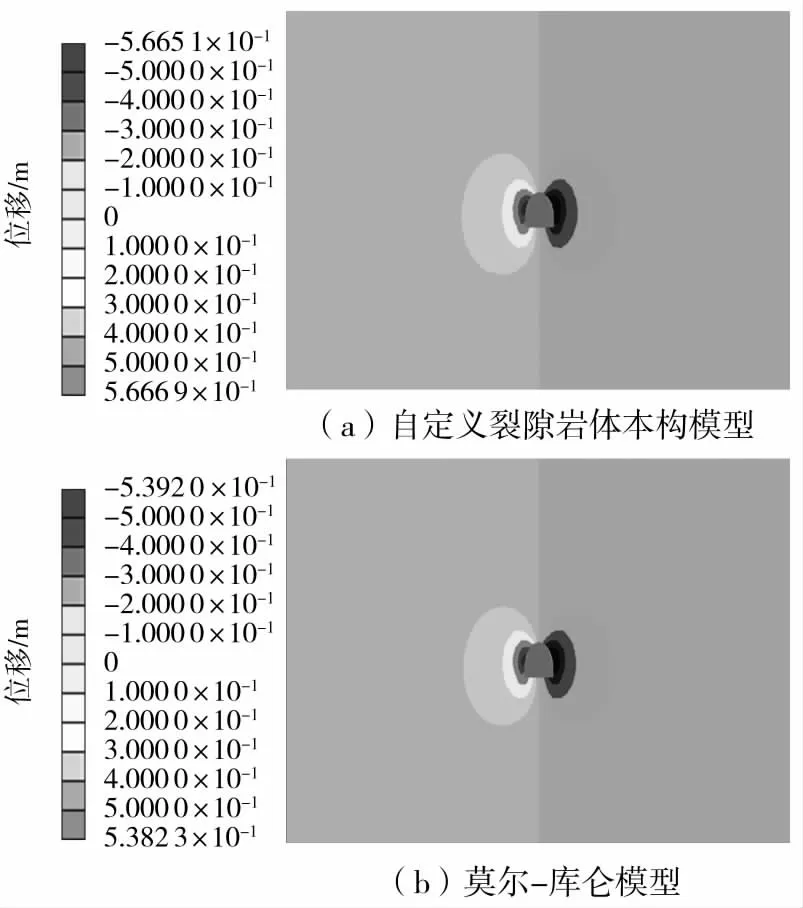
图4 巷道水平位移分布云图
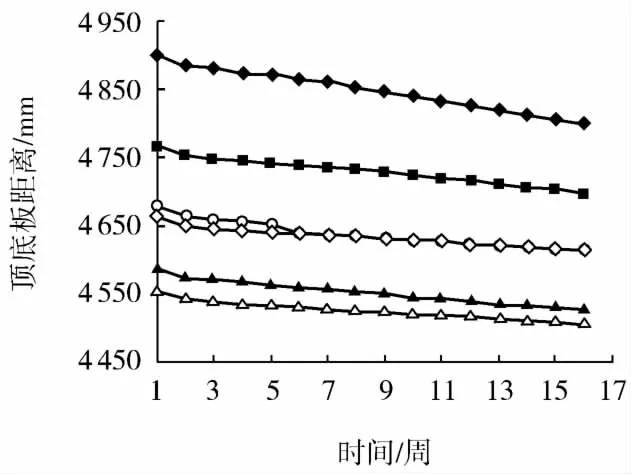
图5 巷道顶底板移近量
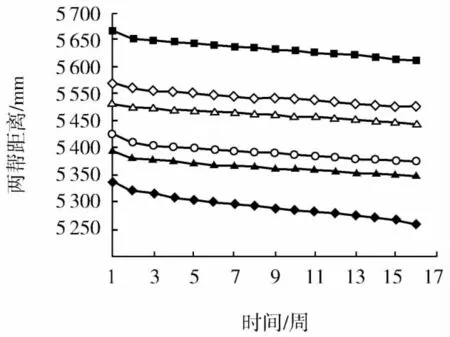
图6 巷道两帮移近量
3 结论
根据裂隙岩体损伤力学原理,研究裂隙岩体在压剪和拉剪应力状态下的损伤演化规律,并根据这一规律模拟出裂隙岩体弹塑性损伤的本构模型。将该模型应用于某实际巷道中,与莫尔-库仑模型的计算结果进行对比,得出裂隙岩体本构模型的位移分布规律均较合理的结论,同时将基于裂隙岩体损伤的本构模型的位移与现场监测到的数据相比较得出基本吻合的结论。因此在工程应用中裂隙岩体本构模型有一定的参考价值。
[1] 易顺民,朱珍德.裂隙岩体损伤力学导论[M].北京:科学出版社,2005.
[2] 周维垣,杨 强.岩石力学数值计算方法[M].北京:中国电力出版社,2005.
[3] 朱珍德,郭海庆.裂隙岩体水力学基础[M].北京:科学出版社,2007.
[4] 周维垣,杨 强.岩石力学数值计算方法[M].北京:中国电力出版社,2005.
[5] 柴红保,曹 平,赵延林,等.裂隙岩体损伤演化本构模型的实现及应用[J].岩土工程学报,2010,32(7):1047-1053.
[6] 伍法权.统计岩体力学原理[M].武汉:中国地质大学出版社,1993.
[7] 蓝 航,姚建国,张华兴.基于FLAC3D的节理岩体采动损伤本构模型的开发及应用[J].岩石力学与工程学报,2008,27(3):572-579.
[8] 郑少河.裂隙岩体渗流场-损伤场耦合理论研究及应用[D].武汉:中国科学院武汉岩土力学研究所,2000.
[9] 中国航空研究院编著.应力强度因子手册[M].北京:科学出版社,1993.
