层次分析法在军事物流中心选址中的运用
2013-06-26张春才吕绍旭顾宏波
张春才,吕绍旭,顾宏波
(后勤工程学院,重庆 401311)
军事物流中心的选址是一个战略问题,在整个军事后勤保障流程中起着连接上游后勤指挥中心、后勤物资生产厂家和下游的各个需求单位的作用。因此,军事物流中心的地位非常重要,合理的选址既可以有效节约建设经费,又可以实现后勤保障中的上下级间的协调与配合,实现快速、准确地保障[1]。层次分析法(Analytical Hierarchy Process)是美国数学家(T.L.Saaty)在20世纪70年代提出的,它是一种定性分析和定量分析相结合的系统分析法,适用于多准则、多目标的复杂问题的决策分析。
一、层次分析法的基本原理
AHP方法首先把问题层次化,按问题性质和总目标复杂的问题分解为各个组成元素,将这些元素按支配关系分组形成有序的递阶层次结构,根据一定的比率标度,通过两两比较的方式,将判断定量化,形成比较判断矩阵,计算确定层次中诸元素的相对重要性。具体是先计算各层指标单排序权值,然后再计算各层指标相对于总目标的组合排序权值,以决定诸元素相对重要性总的顺序。从而得到不同方案的权值,为选择最优方案提供依据。
二、层次分析法的优点和缺点
1.层次分析法的优点
(1)系统性。层次分析法把研究对象作为一个系统,按照分解、比较判断、综合的思维方式进行决策,成为继机理分析、统计分析之后发展起来的系统分析的重要工具。
(2)实用性。层次分析法把定量和定性方法结合起来,能处理许多用传统的最优化技术无法着手解决的实际问题,应用范围很广。同时,这种方法使得决策者和决策分析者能够相互沟通,决策者甚至可以直接使用它,这就增强了决策的有效性。
(3)简洁性。具有中等文化程度的人即可以了解层次分析法的基本原理并掌握该方法的基本步骤,该方法计算也非常方便,并且所得结果简单明确,容易被决策者了解和掌握。
2.层次分析法的缺点
(1)AHP只能用于选择方案,而不能生成方案;主观性太强,从层次结构建立,判断矩阵的构造,均依赖决策人的主观判断,选择,偏好,若判断失误,即可能造成决策失误。
(2)该法中的比较、判断以及结果的计算过程都是较粗糙的,不适用于精度较高的问题。
(3)从建立层次结构模型到给出成对比较矩阵,人的主观因素对整个过程影响很大,这使得有些结果使决策者无法接受。当然可以采取专家群体判断的方法来克服这个缺点。
三、层次分析法的步骤
1.建立问题的递阶层次结构图
在图1中,目标层为最优化的军事物流中心选址方案;准则层为评价军事物流中心选址方案的准则,有环境安全指标、建设技术指标、物资需求指标、军事战略目标;方案层为军事物流中心选址方案。
2.标度及构造两两比较矩阵
判断矩阵是表示针对上一层某要素而言,本层与它有关联的各要素之间的相对优越程度。标度是判断这种重要程度的标志,是指在同一标准下比较两个方案得出的值。在AHP方法中一般选择1~9标度。
3.由判断矩阵计算被比较元素相对权重
把本层各要素对上一层次来说排出优劣顺序,即求出权重,当CR<0.1,认为判断矩阵满足一致性要求,否则需要调整判断矩阵的值。
4.计算各层元素组合权重,并进行一致性检验
利用层次单排序的计算结果,即每一层元素对其上一层各要素的相对权重,进一步计算出层次分析模型中每一层中所有要素相对于目标层的组合权重,这一步是由上而下逐层进行的。最终结果是得出最低层(方案层)元素相对于目标层的组合权重。根据权重的大小即可得到各方案的优劣,从而为选择最优方案、使整个系统达到最优化提供依据。
四、层次分析法在军事物流中心选址中的应用
1.问题的提出
为了在候选的3个地点选定军事物流中心的地址,有关部门对这三个地点进行了考察,给出了有关的数据和资料。主要由以下的因素:军事战略目标因素、物资需求量因素、建设技术因素、环境安全因素。我们就用这四个标准来评判候选地址的满意程度,以便选出满意的地址。
2.构建层次结构图
为解决这个问题,我们首先画出层次结构图,此结构图分为三层:目标层、标准层、决策方案层,如图1所示。
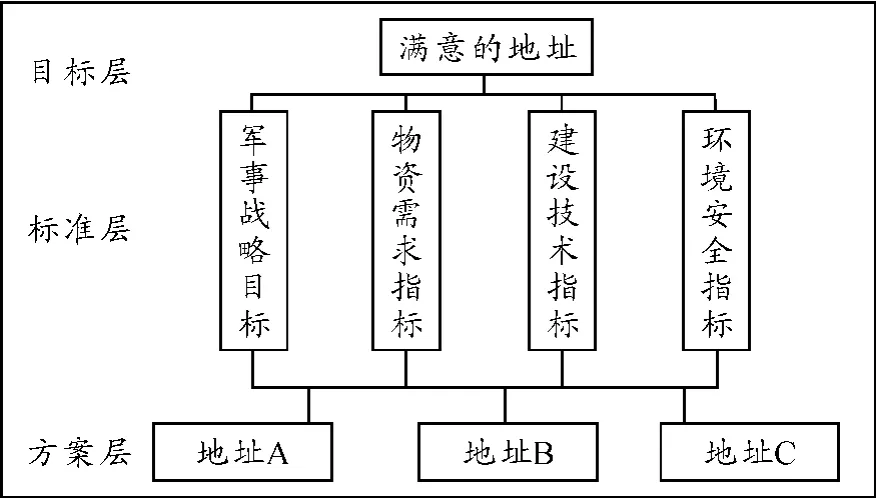
图1 选址层次结构
3.标度及构造两两比较矩阵
为使各个标准两两比较以求得其相对权重,本文引入相对权重的标度,如表1所示。

表1 相对权重的标度
表1中i和j分别表示两个进行比较的标准或在某一标准下比较的两个方案。由标度为元素构成的矩阵称之为两两比较矩阵。方案层的判断矩阵的估计关系到决策质量,因此要选择各个方面的专家参与评估。
用“军事战略目标”标准来评估三个方案,得出决策矩阵如表2。
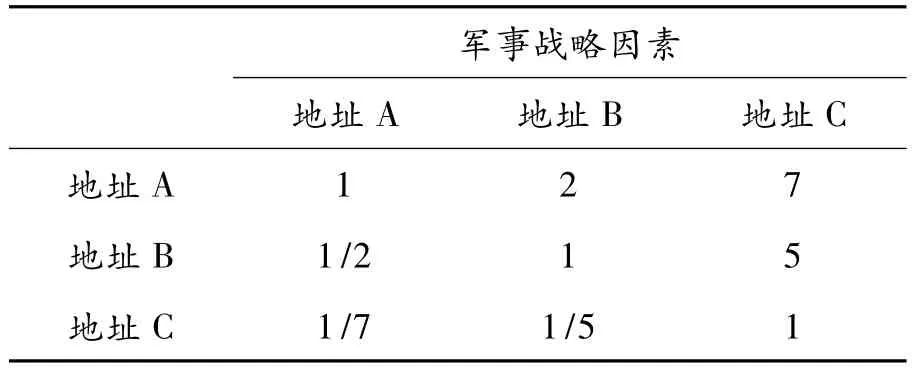
表2 军事战略目标标准决策矩阵
4.求各权重
用两两比较矩阵来求出地址A、B、C在军事战略因素方面的权重。本文使用的是规范列平均法,是一种权重的近似计算法,其他的如方根法、幂乘法就不作介绍了。
第一步:求出两两比较矩阵的每列总和。
第二步:把两两比较矩阵的每一元素除以其相应列的总和,所得商所组成的新矩阵称为标准两两比较矩阵,如表4。
第三步:计算标准两两比较矩阵的每一行的平均值,平均值就是各方案在军事战略因素方面的权重,如表5。

表4 标准两两比较矩阵
从表4中可以得出地址选择问题中军事战略目标方面的特征向量为:
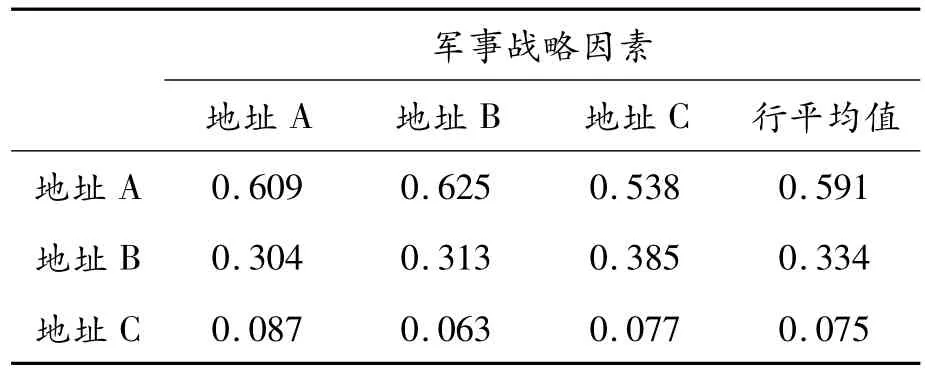
表5 军事战略因素权重
同样的方法可以求得物资需求指标、技术指标、环境安全指标方面的两两比较矩阵,如表6所示。

表6 两两比较矩阵
从表3~6的两两比较矩阵可以求得地址A、B、C在物资需求、建设技术、环境安全三方面的权重,即这三方面的特征向量,如表7所示。
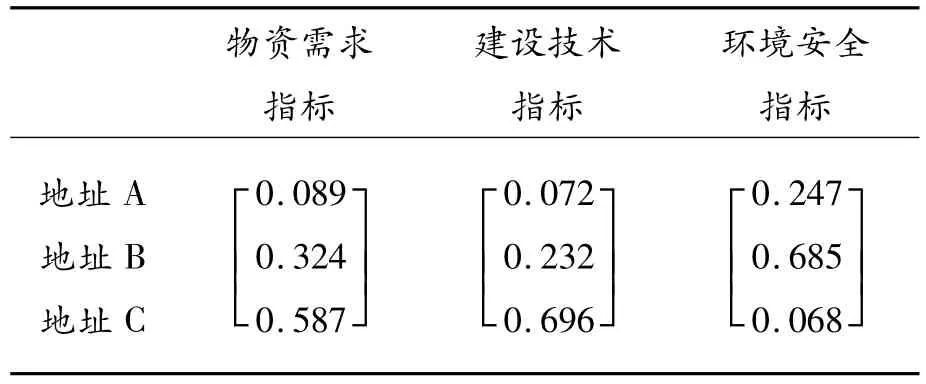
表7 特征向量
另外,还必须取得每个标准在总目标满意的地址相对重要的程度,即是要求得每个衡量标准的相对权重,即评价标准的特征向量。因此,我们把这四个标准比较,取得两两比较矩阵,如表8所示。
通过上面的两两比较矩阵,同样可以求得衡量标准的特征向量,如下所示:

即是军事战略目标的相对权重为0.525,物资需求指标为0.265,建设技术指标为0.061,环境安全指标为 0.155。
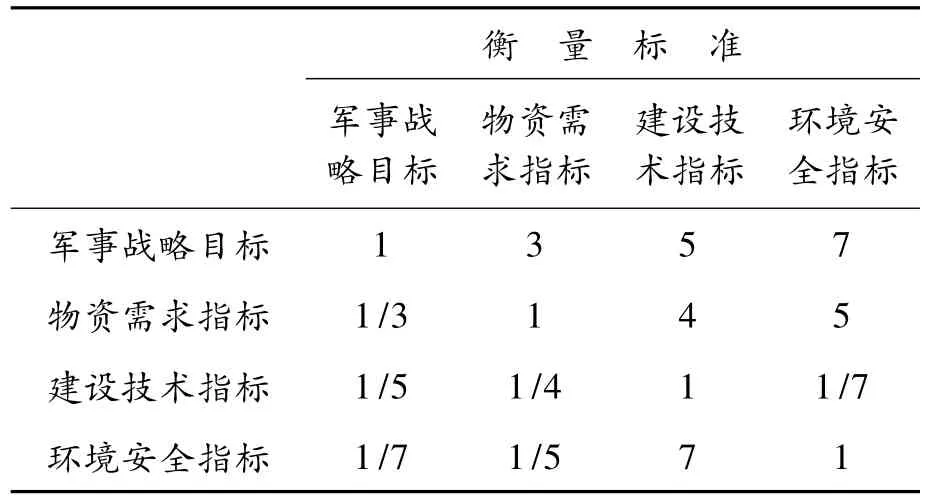
表8 衡量标准两两比较矩阵
5.一致性检验
两两比较矩阵的元素是通过两两比较取得的,在这样的比较中很容易产生一些不一致的结论。如当i,j,k的重要性很接近时,在两两比较中可能得出比j重要,j比k重要,而k又比i重要的矛盾结论,这在考虑因素多的时候更容易发生。要完全达到一致性是非常困难的,因此允许在一致性上有一定的偏差。以军事战略目标为例,具体步骤如下:
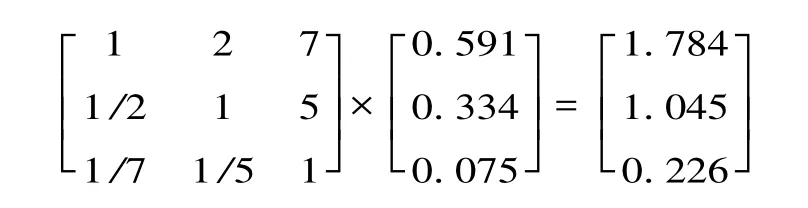
每个赋权和向量的分量分别除以对应得特征向量的分量,
1.784 ÷0.591=3.019
1.045 ÷0.334=3.129
0.226 ÷0.075=3.013
计算上面三个数的均值得:

计算一致性指标CI:

其中n为比较因素的数目,本文中为选址的候选地址,为3。

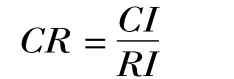
RI是自由度指标,见表9。

表9 自由度指标
计算一致性率CR:
在本文中可以得到:

从上式得出结论,可以认为“军事战略目标”两两比较矩阵满足一致性要求,其相应求得的特征向量为有效。同样可以求得物资需求指标、建设技术指标、环境安全指标以及四个比较标准的两两比较矩阵的一致性率CR值,可以知道他们都小于等于0.10,即其相应求得的特征向量都有效。
6.选取方案
根据求出的四个标准的特征向量和四个单一标准的三个选址方案的特征向量我们可以计算出每个方案的总得分。
地址A 的总得分为:0.591×0.525+0.089×0.265+0.072 ×0.061+0.247 ×0.155=0.377
地址 B 的总得分:0.525 ×0.334+0.265 ×0.324+0.232 ×0.061+0.685 ×0.155=0.381
地址C 的总得分为:0.075 ×0.525+0.265 ×0.587+0.061 ×0.696+0.155 ×0.068=0.248。
通过比较地址B的得分比A稍高,即是B为最优的选址方案。
五、结束语
层次分析法在军事物流中心的选址问题上具有一定的理论价值和实际意义。但层次分析法过分依赖专家评估容易产生偏差,因此具有一定局限性。在考虑有约束条件的多目标、多准则选址问题中,可以将层次分析法和目标规划方法相结合。
