二维三角晶格光子晶体的光子带隙分析
2013-06-25张晓娟
张 晓 娟
(渭南师范学院a.物理与电气工程学院;b.X射线基础研究中心,陕西渭南714000)
光子晶体最基本的特征就是存在光子带隙(photonic bandgap,简称PBG),落在PBG中的电磁波,无论其传播方向如何,都是被禁止传播的.设计性能良好、易控制的PBG非常重要,一般来说,光子晶体的PBG越宽,其性能越好.设计大PBG光子晶体的方法主要是针对某个特定的晶格结构,通过调控其结构参数来实现大PBG优化[1-5],这就限制了优化和设计大PBG研究工作的进一步开展.而影响PBG宽度的因素很多,如晶格结构、材料介电常数、晶格常数、原子半径及缺陷类型等.本文主要采用平面波法[6-7],详细分析影响三角晶格PBG的因素.
1 周期性三角晶格的PBG
对于三角结构晶格中的圆形原子,其单位元为平行四边形,介电常数在倒格子空间的分布不能直接通过倒格矢得到,只能应用数值快速傅里叶变换FFT算法得到.而FFT一般仅用于处理正交空间的问题,要解决非正交空间问题,需要经过坐标变换将非正交坐标系变换到正交坐标系.
三角晶格[8-9]的晶格模型如图1(a)所示.图1(b)为三角晶格的第一布里渊区,图1(c)为三角晶格单位元,对应的单位元经过坐标变换,由非正交坐标系变换到正交坐标系中,得到如图1(d)所示的单位元.Γ、X、M定义了第一布里渊区的基矢量,波矢量k取如图1(b)所示的黑色区域边界.
三角晶格基矢量的选择和正方晶格有所不同,为
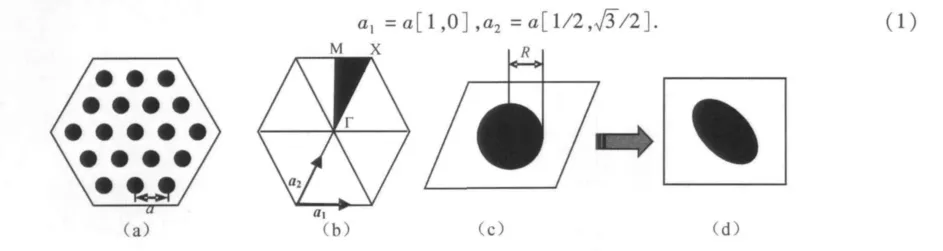
图1 二维三角晶格
为了方便比较[10],选择εa=11.56(磷化铟),εb=1(背景材料为空气),R=0.20a,计算得到周期性三角晶格光子晶体的PBG分布,如图2所示.图中斜线框所示区域为对应的PBG,以下相同,不再重复说明.可以看出,TM波在归一化频率0.28~0.45之间形成PBG,而TE波在归一化频率0.8248~0.8736之间形成PBG.虽然各自都存在PBG,但是相互之间没有重合,不存在完全PBG.即同一种结构的光子晶体,对于同一入射方向不同模式的入射光波的调制不同.这与正方晶格的结果[8]一致.
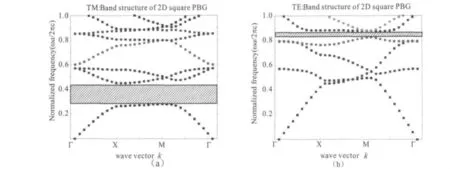
图2 二维三角晶格的PBG分布
2 原子半径R对PBG的影响
选择εa=11.56,εb=1.0,讨论原子半径R不同对PBG的影响.结果如图3(a)所示,其中竖线和点线围起来的区域分别为TM波和TE波所形成的PBG.可以看出,相对于正方晶格而言,三角晶格所形成的PBG更宽,而且,TE波传输时存在PBG,不过仅在R/a比值为0.2附近出现.如果选择εa=1,εb=11.56,则其PBG随原子半径的变化曲线如图3(b)所示,图中竖线区域为TE波形成的PBG,点区域为TM波对应的PBG.可以看出,TE波和TM波在R/a比值0.41之后存在完全PBG,和(a)情况相反,TE波相比TM波更易形成PBG,且TM波对应的PBG范围较窄,仅在空气孔尺寸比较大的情况下.
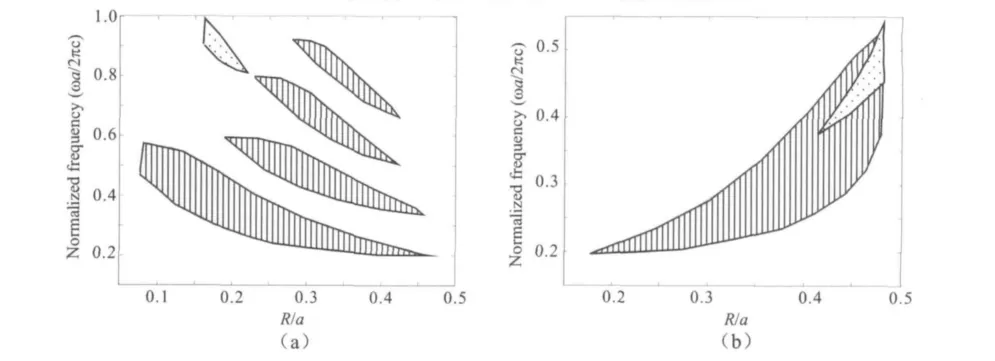
图3 二维三角晶格中PBG随原子半径R的变化
3 原子介电常数εa对PBG的影响
选择R=0.20a,εb=1,改变εa,得到的PBG如图4所示.其中竖线和点线所围区域分别为TM波和TE波形成的PBG.可以看出,TM波和TE波各自形成独立的PBG,但不重合,不存在完全PBG.且随着原子介电常数的增加,TM波的PBG宽度逐渐增加,TE波的PBG宽度逐渐减小.
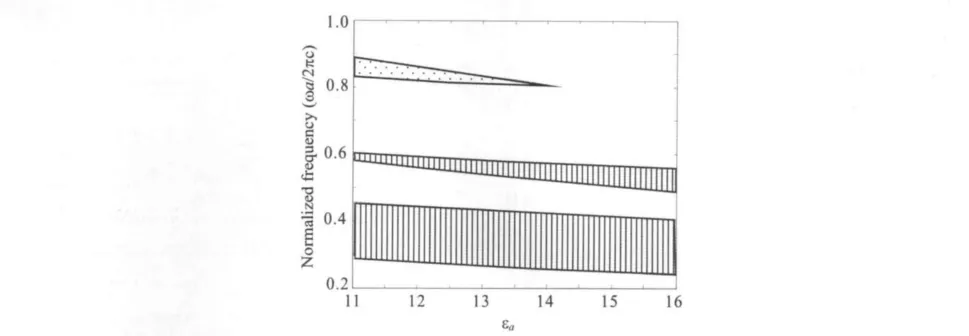
图4 原子介电常数εa对PBG的影响
4 点缺陷对PBG的影响
这里主要讨论两种点缺陷三角结构光子晶体,如图5所示.其中图5(a)为中心去掉一个原子的实心结构,(b)为填充一个大空气孔的空心光子晶体结构.选择参数εa=11.56,εb=1.0,R=0.20a,中心大空气孔半径R1=0.70a.应用超元胞和傅里叶变换等基本理论来实现程序的设计,计算实心三角晶格的PBG,为了清楚地说明问题,这里我们将TM波、TE波所形成的PBG分别做出,结果如图6所示.其中图6(a)和(b)分别为TM波和TE波所形成的PBG,图6(c)是将两者做在一个图上的效果.可以看出,相比没有缺陷的周期性结果(如图2),TM波在原来的PBG中间形成了一个通带,TE波PBG对应的归一化频率降低,如图6(c)所示,形成了两个完全PBG,对应归一化频率范围为0.4158~0.4183及0.4674~0.4869.这与正方晶格的结果有很大不同.
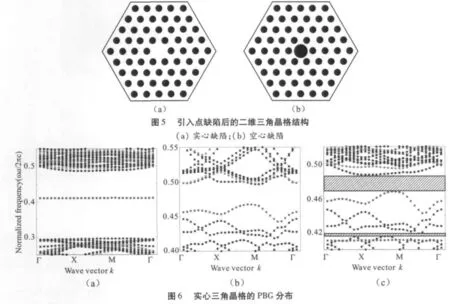
(a)TM波;(b)TE波;(c)TM和TE波
计算得到空心三角晶格的PBG分布如图7所示.同样图7(a)和(b)分别为TM波和TE波所形成的PBG,图7(c)是将两者做在一个图上的效果.可以看出,TM波在PBG中间位置增加了三个通带,TE波PBG的归一化频率也降低,形成三个较窄的PBG,这样入射到光子晶体的光波总可以形成如图(c)所示的三个完全PBG.但相比较而言,其完全PBG的宽度比实心三角晶格的要窄.
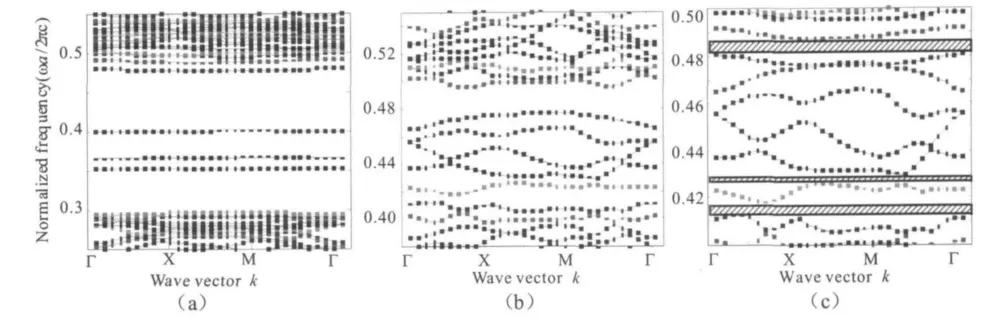
图7 空心三角晶格的PBG分布
5 线缺陷对PBG的影响
在周期性三角晶格光子晶体中去掉中心一排原子,形成如图8(a)所示的线缺陷三角晶格结构.仍选取结构参数εa=11.56,εb=1.0,R=0.2a,得到其能带分布如图8(b)所示.可以看出,不同于正方晶格线缺陷,在光子禁带中间增加了两个通带,但其归一化频率范围很宽,几乎覆盖整个禁带.
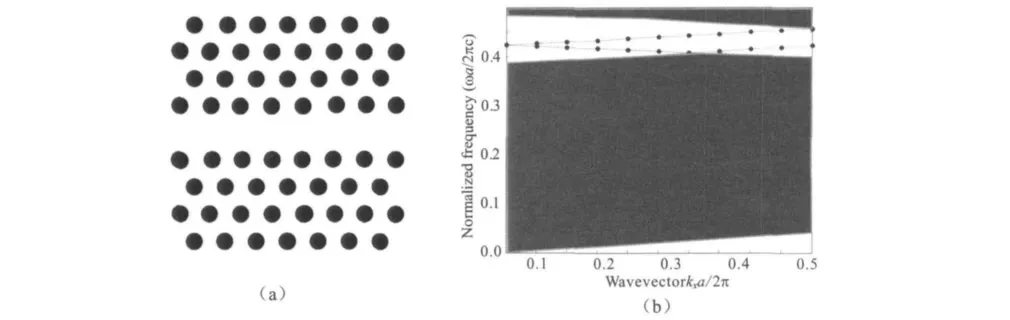
图8 二维三角晶格线缺陷结构及其PBG分布
6 结论
采用平面波法对不同二维三角晶格光子晶体的PBG进行了分析.结果表明,相比正方晶格,三角晶格分布的光子晶体更易形成光子带隙,但一般TM波和TE波所形成的光子带隙并不重合,为了获得完全光子带隙,最好的方式是在周期性光子晶体中引入缺陷.
[1]Yoshino K,Shimoda Y,Kawagishi Y,et al.Temperature tuning of the stop band in transmission spectra of liquid-crystal infiltrated synthetic opal as tunable photonic crystal[J].Appl.Phys.Lett,1999,75(7):932-934.
[2]Zhuang F,Wu L,He S.L.A two-dimensional photonic crystal with six large bandgaps formed by a hexagonal lattice of anisotropic cylinders[J].Chin.Phys,2002,11(8):834-838.
[3]钟凯,张会云,张玉,等,基于六角结构二维光子晶体绝对带隙的优化设计研究[J].物理学报,2007,56(12):7029-7033.
[4]刘剑飞,张伟刚,开桂云,等,可调光子带隙光纤的泄漏损耗特性研究[J].光子学报,2007,36(10):1837-1840.
[5]Pottage J.M,Bird D.M,Hedley T.D,et al.Robust photonic band gaps for hollow core guidance in PCF made from high index glass[J].Opt.Express,2003,11(22):2854-2861.
[6]Guo S P,Wu F,Albin S,et al.Loss and dispersion analysis of microstructured fibers by finite-difference method[J].Opt.Express,2004,12(15):3341-3352.
[7]Guo S P.Photonic crystals:modeling and simulation[D].Virginia:Old dominion university,2003.
[8]Plihal M,Maradudin A A.Photonic band structure of two-dimensional systems the triangular lattice[J].Phys.Rev.B,1991,44(16):8565-8571.
[9]Sakoda K.Optical transmittance of a two-dimensional triangular photonic lattice[J].Phys.Rev.B,1995,51(7):4672-4675.
[10]张晓娟.二维正方晶格光子晶体的光子带隙分析[J].渭南师范学院学报,2012,27(12):37-40.
