三维LOD-FDTD方法在PMC边界处的精确格式*

2013-06-24刘丽娜徐常伟

电讯技术 2013年12期

关键词：立方体导体计算结果

刘丽娜,朱峰,徐常伟

(西南交通大学电气工程学院,成都610031)

三维LOD-FDTD方法在PMC边界处的精确格式*

刘丽娜,朱峰**,徐常伟

(西南交通大学电气工程学院,成都610031)

证明了局部一维时域有限差分(LOD-FDTD)方法实现理想磁导体(PMC)边界时的待求场分量系数与传统的LOD-FDTD方法系数不同。通过在获得该系数前应用理想导体边界条件,得到对应的修正系数。计算了单个PMC立方体和对称的两个PMC立方体的双站RCS。计算结果表明, PMC边界作为理想导体表面时,传统LOD-FDTD方法计算误差较大,采用修正系数的计算结果与传统FDTD方法计算结果更为吻合;PMC边界作为截断计算空间的对称面,采用修正系数的计算结果与传统LOD-FDTD方法计算结果相同。采用修正系数处理PMC边界无需区分PMC边界是理想磁导体表面还是截断计算空间的对称面,具有统一的表达式,计算理想磁导体表面较传统LOD-FDTD方法误差更小。

理想磁导体边界;时域有限差分方法;局部一维时域有限差分方法

1 引言

时域有限差分(FDTD)方法及其改进算法在很多领域得到了广泛应用[1-2],但是Courant-Friedrich -Levy(CFL)稳定条件限制了时间步长,导致传统FDTD方法在数值模拟复杂模型时,所需计算时间过长。基于划分子时间步隐式计算思想的FDTD改进算法,包括局部一维时域有限差分(LOD-FDTD)方法[3]和交替时间隐式时域有限差分(ADI-FDTD)方法[4]等方法,它们能够实现无条件稳定,时间步长的选取不受CFL条件的限制。LOD-FDTD方法将n→n+1的过程分成n→n+1/2和n+1/2→n+1的两个子时间过程,被证明与ADI-FDTD方法有相同的计算精度,且计算时间比ADI-FDTD方法减少55%[5]。LOD-FDTD方法的无条件稳定[6],计算效率[6]、计算误差[7]、相关吸收边界以及与减缩时域有限差分(R-FDTD)方法[8]等相结合的探讨都是研究的热点。人工磁导体在天线领域的应用备受关注[9],PMC边界还可以作为对称面截断计算空间,有效减少内存使用量和计算时间[10]。PMC边界上的切向磁场均为零,当LOD-FDTD计算区域中出现PMC边界时,由于部分场分量被置零,导致待求场分量系数发生变化,如果不对系数进行修正,场分量的计算结果会出现误差。

本文考虑三维LOD-FDTD情况,在得到待求场分量系数之前应用PMC边界条件,推导出LODFDTD方法在理想导体边界处待求场分量的修正系数。对于PMC边界作为理想导体表面和截断计算空间的对称面的不同情况加以区分,讨论了修正系数与传统LOD-FDTD系数的区别。采用修正系数LOD-FDTD方法计算了单个PMC立方体和具有对称结构的两个PMC立方体的双站RCS,计算结果与传统LOD-FDTD方法和FDTD方法的计算结果进行比较,结果表明对于理想磁导体表面,采用修正系数LOD-FDTD方法的计算结果与传统FDTD方法计算结果更为吻合;PMC边界条件作为对称面截断计算空间的情况,采用修正系数LOD-FDTD方法的计算结果与传统LOD-FDTD方法计算结果相同。修正系数LOD-FDTD方法处理PMC边界的优点在于具有统一的表达式,降低了编程复杂度,无需区分PMC边界是理想磁导体表面还是截断计算空间的对称面,计算理想磁导体表面较传统LOD-FDTD方法有较小的计算误差。

2 理论分析

2.1 LOD-FDTD方法

LOD-FDTD方法将FDTD方法中n→n+1的过程分成n→n+1/2和n+1/2→n+1的两个子时间过程:

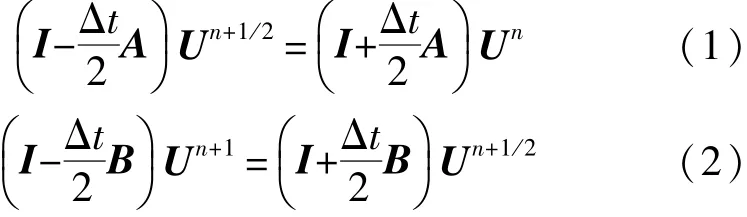
其中,U=[Ex,Ey,Ez,Hx,Hy,Hz]T,I为单位矩阵,矩阵A和B如文献[11]中式(33)和式(34)所示。

将各场分量代入矩阵关系式,可以得到场分量隐式表达式。在n→n+1/2子时间步,Ex和Hz相关联,沿y方向推进;Ey和Hx相关联,沿z方向推进; Ez和Hy相关联,沿x方向推进。由式(1)可以得到n→n+1/2子时间步,仅与Ex和Hz相关的方程:

离散以上两式,得到Ex和Hz的隐式差分方程:

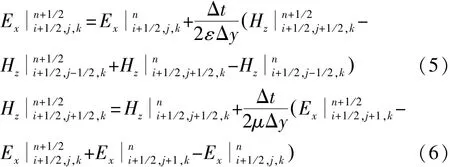
将式(5)中两个n+1/2时刻Hz分量由式(6)表达,整理得到传统LOD-FDTD计算Ex分量的表达式

其中:

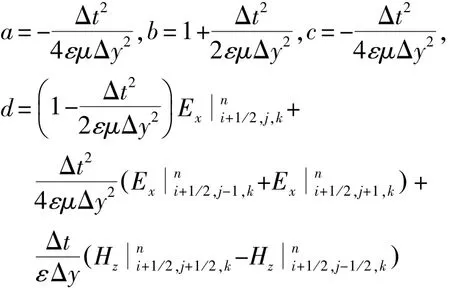
2.2 PMC边界的LOD-FDTD实现

LOD-FDTD方法在n→n+1/2和n+1/2→n+1的两个子时间过程均需要隐式计算电场,再由计算所得电场值,显式计算得到磁场值。LOD-FDTD方法隐式更新电场的特点,决定了PEC边界实现较容易,但PMC边界实现较复杂。下面展开论述三维LOD-FDTD方法实现PMC边界的具体问题。

PMC边界满足切向磁场和法向电场为零的条件,在y=(j0-1/2)Δy处,垂直于y轴设置PMC边界面,分别采用传统LOD-FDTD方法和修正系数LODFDTD方法两种方法处理PMC边界条件。

(1)传统LOD-FDTD方法

得到式(7)之后将PMC边界条件代入:

①如果PMC边界作为理想磁导体表面,则有

②如果PMC边界作为截断计算空间的对称面,应用镜像原理,PMC截断面两侧有可以得到

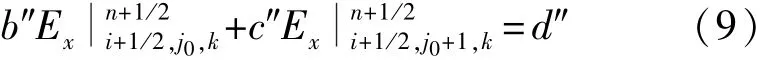
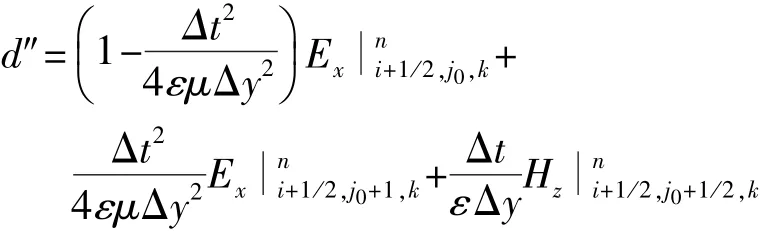
(2)修正系数LOD-FDTD方法

得到式(7)之前,即在式(6)代入式(5)之前考虑PMC边界条件仅将用式(6)展开代入式(5)可以得到

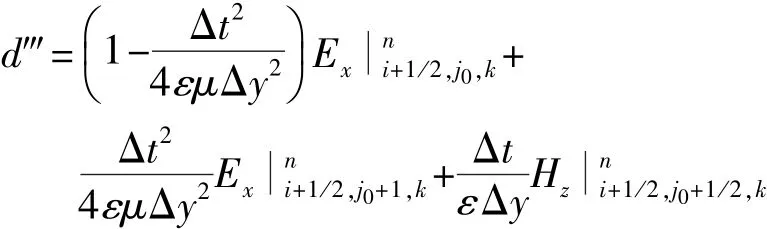
修正系数LOD-FDTD方法不需要区分PMC边界是理想磁导体表面还是截断计算空间的对称面,得到了实现PMC边界的统一格式。对比修正系数LOD-FDTD方法与传统LOD-FDTD方法比较的结果,在处理理想磁导体表面时,等式左端的系数与不同;等式右端的系数,在d‴中为,在d′中为。对于PMC边界作为对称面截断计算空间的情况,截断面的表面虽然同样满足PMC边界条件,但是由于截断面以外的场分量不再为零,修正系数LOD-FDTD方法与传统LOD-FDTD方法表达式相同。n+1/2→n+1的子时间步有类似的情况。

3 数值计算结果

采用修正系数LOD-FDTD方法计算单个PMC立方体和对称的两个PMC立方体的双站RCS,与传统LOD-FDTD方法和FDTD方法的计算结果进行比较。平面波频率3 GHz沿z方向入射,x方向极化。计算空间由PML吸收边界截断。FDTD算法的时间步长Δt=8.333×10-12s,空间步长Δx=Δy=Δz =0.005 m,修正系数LOD-FDTD方法和传统LODFDTD方法的时间步长ΔtLOD=3Δt。

算例1:理想磁导体表面的情况

计算一个PMC立方体的双站RCS,PMC立方体每个面都采用PMC边界条件,立方体边长为L= 0.1 m。计算模型如图1所示,3种方法对比计算PMC立方体的双站RCS如图2所示。分析对比计算结果,对于设置在理想磁导体表面的PMC边界,3种方法的计算结果差别不大,修正系数LOD-FDTD方法的计算结果更接近FDTD方法的计算结果,说明了理想磁导体表面采用修正系数计算的正确性和必要性。

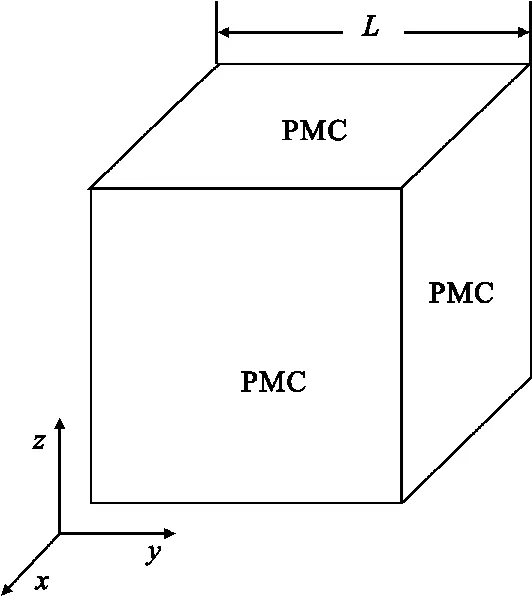
图1 算例1的计算模型Fig.1 The calculation model of Example 1

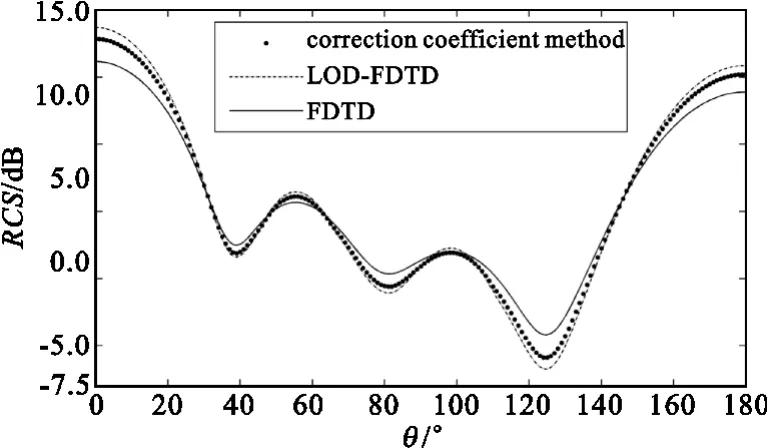
图2 不同方法计算一个PMC立方体的双站RCSFig.2 Different methods comparison of bistatic RCS of a PMC box

算例2:PMC边界截断对称空间的情况

计算对称的两个PMC立方体的双站RCS,每个立方体边长为L=0.1 m,两个PMC立方体中心间距0.2 m。PMC立方体表面均采用修正系数计算。在与y轴垂直的整个计算区域的对称面处设置PMC边界截断,只计算FDTD方法的一半空间。计算模型如图3所示,分别用3种方法处理PMC截断面,对比计算得到的两个PMC立方体的双站RCS如图4所示。

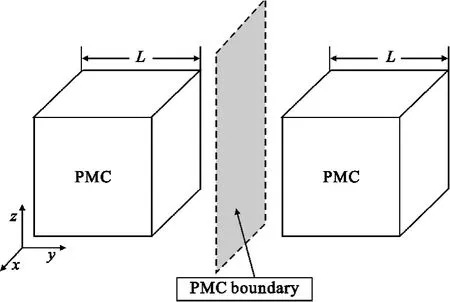
图3 算例2的计算模型Fig.3 The calculation model of Example 2

图4 不同方法计算对称的两个PMC立方体的双站RCSFig.4 Different methods comparison of bistatic RCS of two symmetric PMC boxes

分析对比计算结果,对于PMC边界作为对称面截断计算空间的情况,修正系数LOD-FDTD方法和传统LOD-FDTD方法的计算结果吻合。截断面的表面同样满足PMC边界条件,但是由于截断面以外的场分量不再为零,所以,修正系数LOD-FDTD方法有与传统LOD-FDTD方法相同的表达式。数值计算结果也表明,PMC边界作为对称面截断计算空间,修正系数LOD-FDTD方法和传统LOD-FDTD方法等同。

4 结论

本文考虑三维LOD-FDTD方法,在得到待求场分量系数之前应用理想导体边界条件,推导出在理想磁导体边界处与传统LOD-FDTD方法不同的待求场分量的修正系数。计算了单个PMC立方体和对称的两个PMC立方体的双站RCS,采用修正系数LOD-FDTD方法与传统LOD-FDTD方法和FDTD方法的计算结果进行了对比。数值计算结果表明, PMC边界作为理想磁导体表面时,修正系数LODFDTD方法与传统LOD-FDTD方法相比误差更小; PMC边界作为对称面截断计算空间时,应用镜像原理,修正系数LOD-FDTD方法与传统LOD-FDTD方法等同。修正系数方法处理PMC边界的优点在于具有统一的表达式,降低了编程复杂度,无需区分PMC边界是理想磁导体表面还是截断计算空间的对称面,计算理想磁导体表面较传统LOD-FDTD方法有较小的计算误差。

[1] 冯延彬,李国林,路翠华,等.基于混合信号仿真技术的高功率微波与无线电引信耦合效应分析[J].电讯技术,2013,53(6):807-811.

FENG Yan-bin,LI Guo-lin,LU Cui-hua,et al.Analysis of high power microwaves effect on radio fuse by mixed signal simulation technology[J].Telecommunication Engineering,2013,53(6):807-811.(in Chinese)

[2] 冯延彬,李国林,李春荣,等.基于PSO/FDTD的波导缝隙天线优化设计[J].电讯技术,2013,53(5): 645-649.

FENG Yan-bin,LI Guo-lin,LI Chun-rong,et al.Optimal Design of Waveguide Slot Antenna Based on PSO/ FDTD[J].Telecommunication Engineering,2013,53 (5):645-649.(in Chinese)

[3] Shibayama J,Muraki M,Yamauchi J,et al.Efficient implicit FDTD algorithm based on locally one-dimensional scheme[J].Electronics Letters,2005,41(19):1046-1047.(in Chinese)

[4] Namiki T.3-D ADI-FDTD method-unconditionally stable time-domainalgorithmforsolvingfullvector Maxwell′s equations[J].IEEE Transactions on Microwave Theory and Techniques,2000,48(10):1743-1748.

[5] Liu Q F,Chen Z Z,Yin W Y.An efficient unconditionally stable three-dimensional LOD-FDTD method[C]//Proceedings of 2008 IEEE MTT-S International Microwave Symposium Digest.Atlanta,GA:IEEE,2008:45-48.

[6] Ahmed I,Chua E K,Li E P,et al.development of the three-dimensional unconditionally stable LOD-FDTD method[J].IEEE Transactions on Antennas and Propagation,2008,56(11):3596-3600.

[7] Ahmed I,Chua E K,Li E P.Numerical dispersion analysis of the unconditionally stable three-dimensional LOD -FDTD method[J].IEEE Transactions on Antennas and Propagation,2010,58(12):3983-3989.

[8] 张品,陈亦望,傅强.一种提高内存使用效率的时域有限差分算法[J].电波科学学报,2011,26(4):814 -819.

ZHANG Pin,CHEN Yi-wang,FU Qiang.A memory-efficient FDTD algorithm[J].Chinese Journal of Radio Science,2011,26(4):814-819.(in Chinese)

[9] 鲁磊,屈绍波,马华,等.宽带雷达散射截面减缩人工磁导体复合结构[J].物理学报,2013,62(3):170-175.

LU Lei,QU Shao-bo,MA Hua,et al.A broadband artificial magnetic conductor composite structure for radar cross section reduction[J].Acta Physica Sinica,2013, 62(3):170-175.(in Chinese)

[10] 张岩,吕善伟,苗俊刚,等.FDTD-PWS法用于分析毫米波透镜天线焦面场[J].北京航空航天大学学报,2007,33(6):682-685. ZHANG Yan,LV Shan-wei,MIAO Jun-gang,et al.

Hybrid FDTD-PWS method for focal field analysis of lens antenna at millimeter-wave band[J].Journal of Beijing University of Aeronautics and Astronautics, 2007,33(6):682-685.(in Chinese)

[11] Tan E L.Fundamental schemes for efficient unconditional-ly stable implicit finite-difference time-domain methods[J].IEEE Transactions on Antennas and Propagation,2008,56(1):170-177.

LIU Li-na was born in Tangshan,Hebei Province,in 1981.She received the B.S.degree in 2000.She is currently working toward the Ph.D.degree.Her research concerns electromagnetic scattering and electromagnetic computation.

Email:linaapple329@163.com

朱峰(1963—),男,安徽人,教授、博士生导师,主要研究方向为电磁场与电磁波、电磁场数值计算;

ZHU Feng was born in Anhui Province,in 1963.He is now a professor with the Ph.D.degree and also the Ph.D.supervisor.His research concerns electromagnetic computation,electromagnetic field and wave.

Email:zhufeng@swjtu.cn

徐常伟(1984—),男,河南人,2004年获学士学位,现为西南交通大学博士研究生,主要研究方向为电磁散射、电磁场数值计算。

XU Chang-wei was born in Henan Province,in 1984.He received the B.S.degree in 2004.He is currently working toward the Ph.D.degree.His research concerns electromagnetic scattering and electromagnetic computation.

Accurate Algorithm on PMC Boundary for 3D LOD-FDTD Method

LIU Li-na,ZHU Feng,XU Chang-wei

(College of Electrical Engineering,Southwest Jiaotong University,Chengdu 610031,China)

The field coefficient on perfect magnetic conductor boundary is proved to be different from that in the conventional locally one-dimensional finite-difference time-domain(LOD-FDTD)calculation.The correction coefficient is derived by setting PMC boundary condition before the conventional field coefficient is obtained from the implicit equations.Bistatic RCS calculations of a PMC cube and two symmetrical PMC cubes are provided by using correction coefficient method,conventional LOD-FDTD method and FDTD method,respectively.For the surface of perfect conductor,numerical results of correction coefficient method agree better with those of conventional FDTD.For the symmetry plane truncated computing space,numerical results of correction coefficient method agree well with those of conventional LOD-FDTD.The theory proposed in this paper is validated.Correction coefficient method has unified expressions and it is found that less calculation errors occur than conventional LOD-FDTD method is used.

PMC boundary;finite-difference time-domain(FDTD)method;locally one-dimensional finite-difference time-domain(LOD-FDTD)method

The National Natural Science Foundation of China(No.60971041)

date:2013-09-10;Revised date:2013-11-19

国家自然科学基金资助项目(60971041)

**通讯作者:zhufeng@swjtu.cn Corresponding author:zhufeng@swjtu.cn

TN04;TM153

:1001-893X(2013)12-1638-05