混沌扩频测控系统同步捕获性能分析*

余金峰,杨文革,李 飞,商向永

(1.装备学院,北京101416;2.洛阳电子装备试验中心,河南洛阳471003)

混沌扩频测控系统同步捕获性能分析*

余金峰1,2,**,杨文革1,李 飞2,商向永2

(1.装备学院,北京101416;2.洛阳电子装备试验中心,河南洛阳471003)

混沌序列在扩频测控系统中的应用引起了人们的广泛兴趣,混沌扩频测控系统的捕获性能和跟踪性能是学界关注的重点。由于数字化混沌序列相关函数旁瓣具有随机性,使得扩频系统的信号捕获过程,除了受加性噪声影响之外,又增加了一个影响因素。根据系统捕获原理与混沌码特性,借助于混沌码模糊函数的概念,提出了混沌码相关函数旁瓣随机性影响下检测概率、虚警概率以及捕获时间的计算方法,推导得到了相应的计算公式,探讨了混沌扩频测控系统的信号捕获性能。结果表明,混沌码相关函数随机性的存在使检测概率和虚警概率有所增大,并使捕获时间产生变化;与加性噪声相比,其影响通常较小甚至可以忽略。该结果可以为混沌序列在扩频测控系统中的应用提供理论支持与参考。

测控系统;混沌序列;扩频序列;测距;捕获性能

1 引 言

混沌现象是在非线性动态系统中出现的确定性的类随机过程,这种过程既有界又不收敛,非周期并且对初始值有极其敏感的依赖性[1]。随着非线性理论和混沌理论的不断成熟,混沌学已经由对混沌现象的研究步入了对混沌应用的研究。在通信领域,混沌序列获得了广泛关注。混沌序列可以由简单的映射得到,易于产生,而且混沌序列的随机性、遍历性使其具有良好的平衡性和类似高斯噪声的自相关特性,对初始值的敏感依赖性确保了混沌序列的数目众多,从中可以得到足够多的、有较好相关特性的扩频序列。混沌序列的这些优良特性使得它已成为扩频序列的一种新的来源[2-3]。

近年来,测控领域的研究人员提出了把混沌序列应用到测控系统中的思想,并开展了相关的研究工作[4-6]。本文在已有的研究基础上,分析了混沌序列的特性和优势,探讨了混沌扩频测控系统的同步捕获方法,重点研究包含和忽略混沌序列自相关函数随机性两种情况下系统检测概率和虚警概率的差别,分析混沌序列替换常规伪随机序列后系统捕获性能的变化,为混沌序列在扩频测控系统中的应用提供理论支持和技术参考。

2 混沌扩频测控系统中的同步捕获

扩频信号捕获的核心,就是区分本地码和多普勒频率与输入信号的同步和非同步状态[7-8]。当本地序列和接收序列的相位误差、本地多普勒频率和输入多普勒频率差都小于各自的一个步进时,相关积分的结果要大于其他情况下的积分结果,这是由扩频序列的自相关特性决定的。

直接序列扩频信号的具体捕获方法多种多样。随着数字信号处理技术的发展,扩频信号的捕获方法也在不断变化。截短混沌码与常规扩频码的捕获原理是相同的,现有扩频码的捕获方法对混沌码大多是适用的,只有少数方法不适用(比如序列估计快速捕获法)。在伪码捕获算法中,基于相关值进行处理的方法称为传统捕获方法,这些仍然是目前应用比较广泛的方法。本文以传统捕获法中的顺序相位搜索捕获算法为例,分析混沌序列相关函数旁瓣随机性对虚警概率、检测概率和捕获时间的影响。

顺序相位搜索法只用一个相关器实现捕获。设相关器的积分时间为T,在0～T时间内积分,结果输出送给门限比较器,积分器输出值小于门限时,表示本地参考扩频码序列的相位和接收扩频码序列相位不相同。相位搜索控制器控制本地参考扩频码产生器改变输出序列的相位状态,改变量为半个码元,再次检测积分器输出值。不断地改变本地参考扩频码产生器的相位状态,直到相关器的积分值超过设定的门限而达到最大,表示本地参考扩频码序列的相位与接收扩频码序列的相位一致,实现了扩频码序列的同步捕获。

设扩频码码长为N,搜索步进为半个码元。H0表示未同步状态,H1表示同步状态,H0的虚警概率为Pfa,H1的检测概率为Pd。引用文献[9]中的结果,由马尔可夫链来推导的平均捕获时间公式为

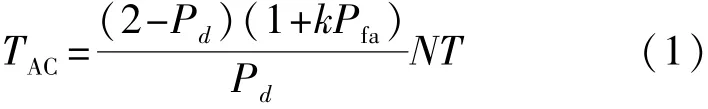
式中,k为虚警惩罚次数,它将虚警情况下的惩罚进行了限定。平均同步时间与检测概率、虚警概率和积分时间和需要搜索的码元数有关,也与虚警惩罚次数k有关。为了突出虚警概率和检测概率的作用,将平均捕获时间表示为NT的倍数,倍数Times of NT用TAC1表示:

由上式可以看出,平均捕获时间TAC与虚警概率Pfa、检测概率Pd和积分时间T有关。当H0检测的虚警概率Pfa为0时,平均捕获时间取决于检测概率Pd;当H1的检测概率Pd为1时,平均捕获时间取决于虚警概率Pfa;当检测概率为1、虚警概率为0,也就是完全理想情况下,平均捕获时间为NT。

3 虚警概率和检测概率

扩频信号的捕获就是要区分同步和非同步两种状态,对接收信号要进行载波剥离和扩频码去除两个处理过程,并采用同相与正交处理模式消除载波相位偏差的影响。捕获原理如图1所示。

图1 信号捕获原理图Fig.1 Diagram of DSSS signal acquisition

图中,r(t)为输入信号,l(t)为本地中频信号, x(t-^τ)为本地混沌扩频信号,~S为相关器输出信号, Ro为判决门限。

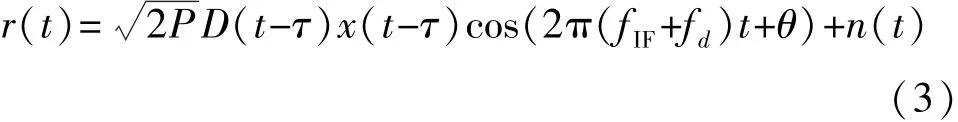
其中,P为信号功率,D(t)为数据码,x(t)为混沌码, fIF、fd、θ分别为中频、多普勒频移和载波初相,n(t)为带限高斯白噪声(均值为零,双边带功率谱密度为N0/2)。

积分时间T应当小于数据位的时间间隔,它的设置应尽量避免使积分跨越数据位边界。为方便起见,假设积分时间T内,数据位D=1。

其中,^fd、^θ分别为多普勒频移和载波初相的估计值。复相关器输出~S为

其中,Δ为各量的估计误差,~η为服从N(0,N0/T)的复高斯随机量。

将复相关器输出~S用x(t)的模糊函数~R[12]表示,可得

式中,~R(Δτ,Δfd)是混沌码x(t)的模糊函数。它的形式与相关函数类似,同时还包含了多普勒频率误差的影响,也就是说它综合了多普勒误差Δfd和码相位误差Δτ的共同作用,而这正是接收机在捕获阶段所要关注的两个变量。

可以将复相关器的输出~S分解为随机分量和非随机分量两部分,非随机部分为P exp(jΔθ) E{},随机部分为′,由的随机性和共同组成:

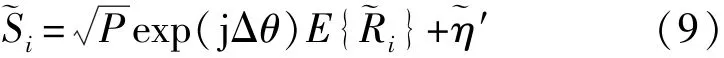
可以近似认为~η′的实部和虚部为相互独立的零均值高斯随机变量,从而可得~η′的方差为Pvar{~Ri}+N0/T。

所以,复相关器输出~S的模近似服从莱斯分布,其模的平方形成的判决量的概率密度函数[10-11]为

其中,I0(·)为零阶修正贝赛尔函数,mi为~Si均值的模,为~Si的方差。由此得到检测概率和虚警概率分别为

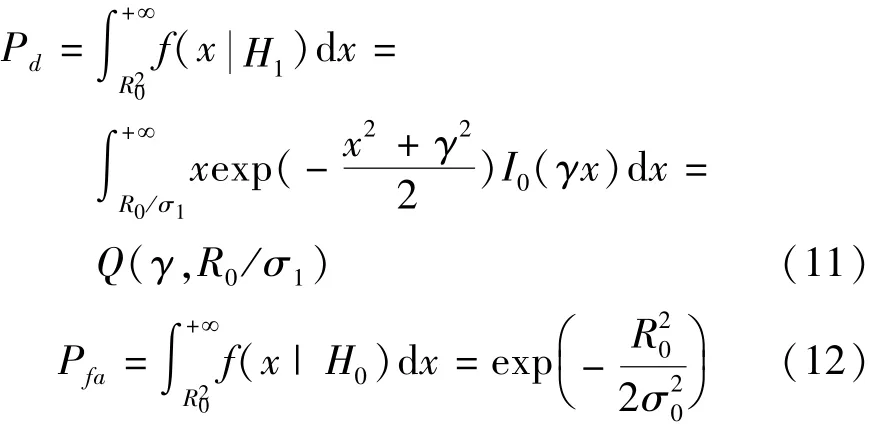
4 混沌扩频测控系统捕获性能

检测概率Pd和虚警概率Pfa是平均捕获时间的主要影响因素。可以看出,Pd、Pfa与复相关器输出~S的均值和方差有关,同步和非同步两种状态下,公式中的参数是不同的。考虑或忽略混沌码相关函数旁瓣随机性,对检测概率和虚警概率也有影响。

4.1 考虑混沌码自相关函数随机性

利用混沌序列的随机性可以求得模糊函数~R的均值E{~R}和方差var{~Ri}[3,12]:

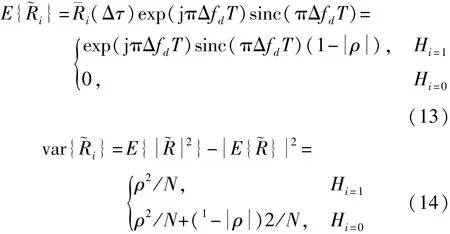
从而可以得到f(x Hi)中的mi和

检测概率和虚警概率计算式中的参数为

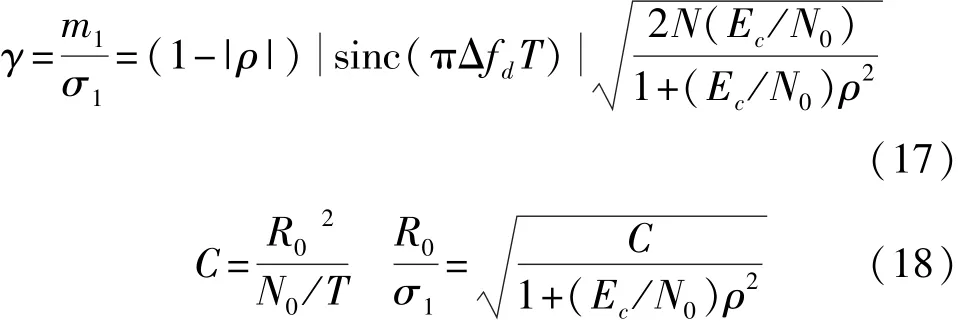
其中,Ec/N0为码元能量噪声功率谱密度比,C为对噪声方差进行归一化的门限值,N为扩频码码长。

4.2 忽略混沌码自相关函数随机性

忽略混沌码自相关函数随机性以后,均值mi与前述一样,没有变化,仅仅是其方差与前不同:

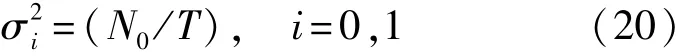
所以,在检测概率和虚警概率的计算公式中,相应的参数也要有所变化:

5 系统捕获性能的计算分析

根据以上公式,可以计算出考虑和忽略混沌码相关函数随机性时,虚警概率、检测概率和平均捕获时间随几个参数的变化关系,比如,多普勒频移ΔfdT、相对时延差ρ、信噪比Ec/N0、归一化门限C等。

计算检测概率、虚警概率时的参数设置为:ΔfdT =0.3,ρ=0.1,C=5,Ec/N0=-10 dB,计算捕获时间时还需要设定惩罚因子k,设k=5,伪码长度N为256。计算时,考察某一参数变化时捕获性能的变化,则所选参数根据要求而变化,其他参数按照设置取值。Pd(1)为考虑自相关函数随机性的检测概率,Pd(0)为忽略自相关函数随机性的检测概率, Pfa(1)为考虑自相关函数随机性的虚警概率,Pfa(0)为忽略自相关函数随机性的虚警概率。结果如图2～5所示。

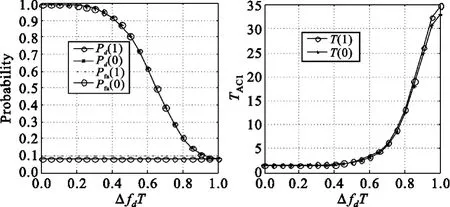
图2 两种情况下Pd、Pfa和NT倍数随ΔfdT的变化Fig.2 Pd,Pfa,TAC1versus ΔfdT with/without correlation randomicity

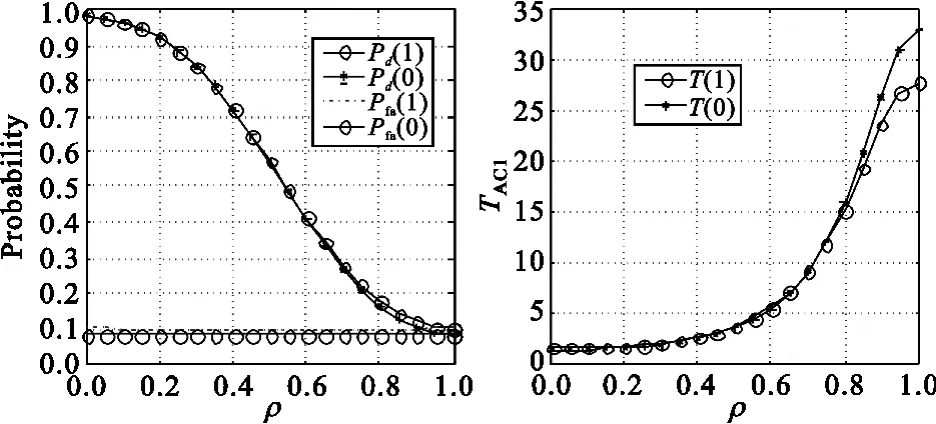
图3 两种情况下Pd、Pfa和NT倍数随ρ的变化Fig.3 Pd,Pfa,TAC1versus ρ with/without correlation randomicity

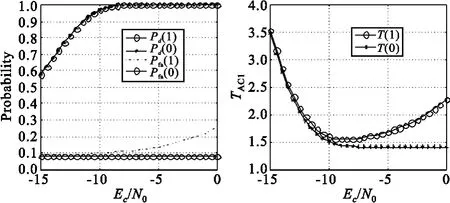
图4 两种情况下Pd、Pfa和NT倍数随Ec/N0的变化Fig.4 Pd,Pfa,TAC1versus Ec/N0with/without correlation randomicity

图5 两种情况下Pd、Pfa和NT倍数随C的变化Fig.5 Pd,Pfa,TAC1versus C with/without correlation randomicity

由以上结果可以看出,忽略混沌序列自相关函数的方差后,会使得虚警概率降低,检测概率增高,并造成系统平均捕获时间的变化。以信噪比的变化对系统平均捕获时间的影响来说,在信噪比较低时,两者的差别很小,信噪比增大时,两者的差别逐渐显现。在Ec/N0=-10 dB时,检测概率分别是0.967 3和0.967 4,虚警概率分别为0.099 2和0.082 1,平均捕获时间分别为NT的1.597 2倍和1.505 6倍,考虑序列自相关函数随机性后,平均捕获时间增大了约6%,通常这是可以接受的结果。在Ec/N0≥-10 dB时,考虑自相关函数的方差时,平均捕获时间增大比较明显;但此时信噪比较高,信号情况良好,检测概率比较高,只是由于混沌码随机性引起的虚警概率变大,从而引起平均捕获时间变大。此时,可以调整门限值C,降低虚警概率。

所以,可以用混沌序列代替现有系统中的伪随机序列,并忽略混沌序列自相关函数的随机性,对捕获结果造成的影响有限,用混沌序列代替现有系统中的扩频序列是可行的。

6 结束语

混沌码的捕获原理与其他扩频码是相同的,所以现有伪码的捕获方法对混沌码来说大多是适用的。文中以顺序相位搜索法为例,分析了平均捕获时间与检测概率、虚警概率的变化关系,研究了非相干平方律检测系统的检测概率、虚警概率与各个系统变量(多普勒频移、码相位误差、门限、信噪比)之间的关系,重点考察了包含和忽略混沌码自相关函数随机性两种情况下检测概率、虚警概率以及平均捕获时间随各参数的变化,并比较了两者的差别。数值仿真结果表明,忽略自相关函数随机性对虚警概率的影响要大于对检测概率的影响,但两者数值都不大,对平均捕获时间的影响也有限。也就是说,在扩频测控系统中,用混沌码替代现有PN码是可行的,不用对系统作过多改动,可以最大限度地利用现有设备和同步捕获方法,同时,系统捕获性能的变化也是可以接受的。文中的内容偏重于混沌扩频测控系统捕获性能的理论分析,其方法与结论的正确性与实用性将在下一步的硬件实现与工程实验中加以检验验证。

[1] Schuster H G.Deterministic Chaos,An Introduction (Second Revised Edition)[M].Federal Republic of Germany:VCH,1988:37-69.

[2] 王亥,胡健栋.改进型Logistic-map混沌扩频序列[J].通信学报,1997,18(8):71-77.

WANG Hai,HU Jian-dong.The improved Logistic-map [J].Journal on Communications,1997,18(8):71-77. (in Chinese)

[3] 余金峰,杨文革,路伟涛,等.满映射Logistic数字混沌序列的产生与特性分析[J].电讯技术,2013,53(2): 140-145.

YU Jin-feng,YANG Wen-ge,LU Wei-tao,et al.The generation and performance analysis of digital chaotic sequence from surjective Logistic-Map[J].Telecommunication Engineering,2013,53(2):140-145.(in Chinese)

[4] 舒卫平,王万斌.混沌码用作测控扩频码的可行性研究[J].航天器工程,2008,17(4):46-50.

SHU Wei-ping,WANG Wan-bin.Research on the Feasibility of Applying the Chaotic Code to the TT&C System as the Spread-spectrum Code[J].Spacecraft Engineering,2008,17(4):46-50.(in Chinese)

[5] 刘嘉兴,文吉.Ka频段混沌扩频测控系统的设想[J].电讯技术,2009,49(5):33-37.

LIU Jia-xing,WEN Ji.Conception for a Ka-band Chaotic Spread Spectrum TT&C System[J].Telecommunication Engineering,2009,49(5):33-37.(in Chinese)

[6] 刘嘉兴,何世彪.混沌测控的概念、特性与实现[J].飞行器测控学报,2011,30(1):1-5.

LIU Jia-xing,HE Shi-biao.Basic concept of chaotic TT&C and main features of chaotic sequence[J].Journal of spacecraft TT&C technology,2011,30(1):1-5. (in Chinese)

[7] 沈允春.扩谱技术[M].北京:国防工业出版社,1995:17.

SHEN Yun-chun.Spread spectrum technology[M].Beijing: National Defense Industry Press,1995:17.(in Chinese)

[8] 田日才.扩频通信[M].北京:清华大学出版社, 2007:198.

TIAN Ri-ca.Spread spectrum communication[M].Beijing:Tsinghua University Press,2007:198.(in Chinese)

[9] Holmes J K.相干扩展频谱系统[M].梁振兴,蔡开基,译.北京:国防工业出版社,1991:135-138.

Holmes J K.Coherent spread spectrum system[M].Translated by LIANG Zhen-xing,CAI Kai-ji.Beijing:National Defense Industrial Press,1991:135-138.(in Chinese)

[10] 孟生云,杨文革,王金宝,等.DS/FH扩频测控信号同步方案的捕获性能[J].宇航学报,2010(8):2036-2042.

MENG Sheng-yun,YANG Wen-ge,WANG Jin-bao,et al.Acquisition Performance of a Synchronization Scheme of DS/FH Spread Spectrum TTC Signals[J].Journal of Astronautics,2010(8):2036-2042.(in Chinese)

[11] Polydoros A,Weber C L.A unified approach to serial search spread spectrum code acquisition-Part II[J]. IEEE Transactions on Communications,1984,32(5): 550-559.

[12] Misra P,Enge P.全球定位系统-信号、测量与性能[M].罗鸣,曹冲,肖雄兵,等,译.北京:电子工业出版社,2008:277-279.

Misra P,Enge P.Global Positioning System Signals, Measurements,and Performance[M].Translated by LUO Ming,CAO Chong,XIAO Xiong-bing,et al.Beijing:Publishing House of Electronics Industry,2008:277 -279.(in Chinese)

作者简介:

余金峰(1969—),男,河南唐河人,2001年于国防科技大学获硕士学位,现为高级工程师,博士研究生,主要研究方向为航天器测量与控制;

YU Jin-feng was born in Tanghe,Henan Province,in 1969.He received the M.S.degree from National University of Defense Technology in 2001.He is now a senior engineer and currently working toward the Ph.D.degree. His research concerns spacecraft TT&C.

Email:yujinfeng2008@sohu.com

杨文革(1966—),男,江西金溪人,2000年于北京理工大学获博士学位,现为教授、博士生导师,主要研究方向为航天测量与控制、雷达信号处理;

YANG Wen-ge was born in Jinxi,Jiangxi Province,in 1966.He received the Ph.D.degree from Beijing Institute of Technology in 2000.He is now a professor and also the Ph.D. supervisor.His research interests include spacecraft TT&C and radar signal processing.

李 飞(1979—),男,河南镇平人,2006年于国防科技大学获硕士学位,现为工程师;

LI Fei was born in Zhenping,Henan Province,in 1979. He received the M.S.degree from National University of Defense Technology in 2006.He is now an engineer.

商向永(1987—),男,河北保定人,2012年于国防科技大学获硕士学位,现为助理工程师。

SHANG Xiang-yong was born in Baoding,Hebei Province,in 1987.He received the M.S.degree from National University of Defense Technology in 2012.He is now an assistant engineer.

Acquisition Performance Analysis of Chaotic Spread Spectrum TT&C System

YU Jin-feng1,2,YANG Wen-ge1,LI Fei2,SHANG Xiang-yong2

(1.The Academy of Equipment,Beijing 101416,China; 2.Luoyang Electronic Equipment Test Center,Luoyang 471003,China)

Chaotic sequence used as the spread spectrum code in spread spectrum system has gained widespread attention because of its excellent characteristics.Besides the bit error rate(BER),which is the main consideration in spread spectrum communication systems,the acquisition and tracking performances are more important in spread spectrum Telemetry Tracking and Control(TT&C)system.In spread spectrum system,signal acquisition is affected by not only additive white Gaussian noise(AWGN),but also the randomness of digital chaotic sequence.The signal acquisition performance is analyzed in this paper.With the aides of chaotic sequence ambiguity function,the effections of chaotic sequence randomicity on detection probability,false alarm probability and acquisition time are studied.According to the results in this paper, the effection of chaotic sequence correlation randomicity is neglectable compared with that of AWGN.The results in this paper provide support and reference for the application of chaotic sequence in TT&C system.

TT&C system;chaotic sequences;spread-spectrum sequences;ranging;acquisition performance

date:2013-09-18;Revised date:2013-11-20

**通讯作者:yujinfeng2008@sohu.com Corresponding author:yujinfeng2008@sohu.com

TN911

:A

:1001-893X(2013)12-1545-06

10.3969/j.issn.1001-893x.2013.12.001

2013-09-18;

2013-11-20