基于有限域的QC-LDPC码编码协作通信及其联合迭代译码技术*

2013-06-24仰枫帆

电讯技术 2013年12期

关键词：译码中继校验

程浩,仰枫帆

(南京航空航天大学电子信息工程学院,南京210016)

基于有限域的QC-LDPC码编码协作通信及其联合迭代译码技术*

程浩**,仰枫帆

(南京航空航天大学电子信息工程学院,南京210016)

为了提高系统的性能和易于工程实现,提出了基于有限域加群构造的QC-LDPC码,通过特殊的构造方法构造出满秩的QC-LDPC码并将之应用于编码中继协作通信系统的源节点和中继节点处,并由此构成了总体校验矩阵,导出了双层Tanner图,目的节点处采用基于双层Tanner图的联合迭代译码算法。仿真结果表明,误码率为10-5、迭代5次时,理想中继协作通信系统的性能好于非协作和非理想中继协作系统的性能,分别为1.3 dB和1 dB;并且S-D与R-D信道的信噪比相等时,S -R信道信噪比越高,非理想中继协作通信系统的性能越好。

协作通信;有限域加群;QC-LDPC码;双层Tanner图;联合迭代译码

1 引言

协作通信技术[1-4]作为多天线技术的扩展,近些年来已经成为通信领域的研究热点,将成为移动通信系统中提高频谱利用率的重要途径之一。协作技术的核心是利用通信网络中多个节点之间的彼此协作,实现路径共享,提高整个通信网络的信道容量,使得在多跳无线通信网中的单天线终端可以有效地抵抗信道衰落,从而通过分布的天线获得空间分集增益,又因多跳的方式降低了功率损耗。

目前协作通信一共有3种方式,即放大转发、检测转发[3]和编码协作[4]。Hunter在2006年最先提出了编码协作模式,并研究了Turbo码编码协作系统的性能。与Turbo码编码协作系统相比,LDPC码编码协作系统[5-7]具有译码复杂度低和硬件实现简单等特点。QC-LDPC码[8]是一类具有低编码复杂度和硬件实现资源消耗低的LDPC码,目前已经被广泛应用于DVB-S2、802.11n/16e,以及CMMB等众多标准。本文将QC-LDPC码应用于中继编码协作通信中,提出了基于有限域加群[9]构造出的满秩QC-LDPC校验矩阵的方案,目的节点采用基于双层Tanner图的联合迭代译码算法,加快了译码收敛速度,提高了系统性能,并且易于在工程上实现。

2 中继信道下基于QC-LDPC码编码协作通信系统

中继信道下基于QC-LDPC码编码协作通信系统模型如图1所示。将要被传输的源信息序列在源节点S处经编码器1编码,然后通过BPSK调制后发送出去。该序列通过源节点S与目的节点D间的S-D信道直接传送至目的节点,同时通过S-R信道发送至中继节点R处。中继节点R包含两个组成部分:译码器1和编码器2。译码器1将接收到的受到噪声干扰的序列进行正确译码,然后送至编码器2重新编码。经过BPSK调制后通过R-D信道发送至目的节点D。目的节点接收两路信号后,利用两路信号的不相关性,根据一定的方案联合译码,以获得更好的译码性能。

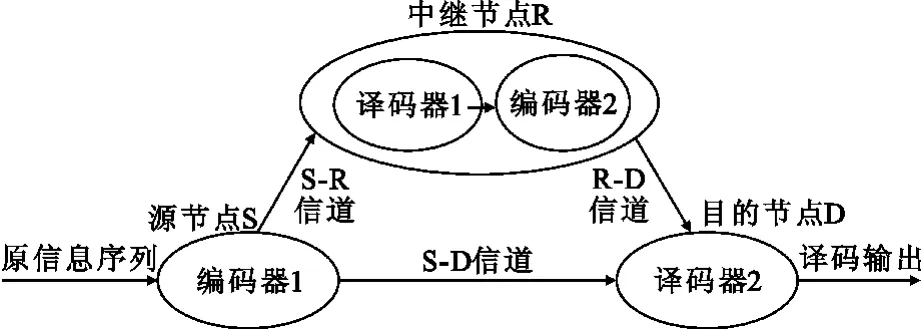
图1 基于QC-LDPC码编码协作通信系统模型Fig.1 The QC-LDPC-Based encoding cooperative communication system model

3 QC-LDPC码协作编码方式

中继信道下基于QC-LDPC码的编码协作通信系统的编码实现方式如下:如图1所示,在源节点S处使用M1×N的校验矩阵H1对输入信息序列编码,生成长度为N的码字序列c1=(c1,c2,…,cN)T,与输入信息序列相比增加了长度为M1的校验位。

中继节点R接收受到S-R信道噪声干扰的信号通过译码器1译码。译码结果作为新的信息序列输入到编码器2并使用M2×(N+M2)的校验矩阵H2再次编码生成码长为N+M2的码字序列c2=(c1,c2,…, cN,p1,p2,…,pM2)T,我们将矩阵H2写成如下形式:

分别通过S-D信道与R-D信道将c1的整个码字和序列c2的校验位部分p=(p1,p2,…,pM2)T发送至目的节点D处。根据校验关系得

由上式可得编码协作系统的整个码字c满足下述校验关系:

其中,c是由c1的整个码字和序列c2的校验位部分p=(p1,p2,…,pM2)T组成的长度为N+M2的复合码字,H是由校验矩阵H1和H2决定的矩阵,它们分别表示如下:

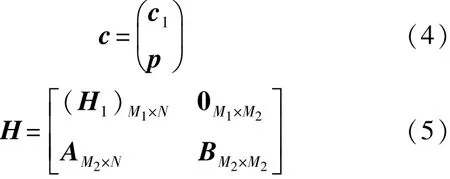
4 基于有限域加群的QC-LDPC码的校验矩阵H构造

本小节主要介绍基于有限域加群的QC-LDPC码的构造以及寻找满足条件的H校验矩阵。

4.1 基于有限域加群的QC-LDPC码的构造

设q是质数,于是整数集{0,1,2,…,q-1}在模q乘法和模q加法运算下构成了有限域GF(q),又称之为原始域。对于有限域GF(q)中的每个元素i,它的位置矢量定义为GF(2)内的q维单位向量,记为z(i)=(z0,z1,…,zq-1),其中1的位置与GF(q)中的元素一一对应。显然,对于GF(q)中的任意元素i,i+1的位置矢量z(i+1)是i位置矢量z(i)的右循环移位一位得到的。

下面给出构造QC-LDPC码的基本步骤。

Step 1:构造在GF(q)上的q×q的基矩阵w,其中i和j的乘法执行的是模q相乘。

Step 2:将上面基阵w的每一行的每一个元素垂直地依次加上GF(q)中的元素,基阵的每一行都被扩展成一个GF(q)上的q×q的矩阵,如下式所示:

其中,矩阵的每一个元素执行的都是模q相乘相加运算。显然,其每列的q个元素都是不同的。wi称为w的第i行wi相加q对折垂直扩展。将wi的每个元素用对应的位置矢量替代,于是得到有q个q× q循环置换矩阵元素的行矩阵,记为Bi=[Qi,0Qi,1Qi,2…Qi,q-1],其中Qi,j由wi的第j列元素的位置矢量替换构成。将wi的第j列元素用对应的位置矢量替代称为相加q对折水平扩展。

Step 3:扩展矩阵w得到GF(2)上的q×q循环置换矩阵构成的q×q校验矩阵:

显然,Q是GF(2)上的q2×q2的矩阵,行列重均为q且不包含0子矩阵。

Step 4:从Q中选择循环子矩阵构造满足行重列重要求的QC-LDPC校验矩阵Qqc。对于行重为ρ列重为λ的的QC-LDPC码,通常选取Q中λ×ρ的循环子矩阵构造Qqc。

需要说明的是,构造出来的Qqc的环长至少为6,我们只需要证明矩阵Q不存在四环即可。用反证法证明如下。

证明:假设Q中存在四环,那么在Q的某个矩形的四角存在4个1分量,由于Q是一个准循环矩阵,这4个分量分别存在于4个不同的子矩阵Qi,s, Qi,t,Qj,s和Qj,t中,其中0≤i,j,s,t＜q,且i≠j,s≠t,不妨设i＜j,s＜t。特别地,假设1分量在Qi,s和Qi,t的第k行、Qj,s和Qj,t的第l行。又因为循环矩阵Qi,s,Qi,t, Qj,s和Qj,t由分量分别为i·s,i·t,j·s,j·t经过相加对折垂直和水平扩散得到。于是有i·s+k+mq= j·s+l(m≥0),i·t+k+nq=j·t+l(n≥0),从以上两式可以得到(j-i)(t-s)=(n-m)q,于是又可以得到[(j-i)(t-s)]mod q=0,由于q为质数,与已知条件矛盾,故Q中不存在四环。证毕。

4.2 校验矩阵H的构造步骤

在本文中仿真采用的数据为q=127,源节点处发送的码字码长为2 032,中继节点处编好的码字码长为4 064。

(1)为了满足要求,矩阵H1和H2可以设定为如下结构:

其中,Pi,j为循环置换矩阵,Di为d=3个q×q的单位矩阵右移si,j位而成,即。其中d为奇数,确保Di可逆,从而矩阵H′可逆,满足这种结构的校验矩阵高斯消元不需要交换列,避免了信息位不匹配的情况。

(2)由于Q矩阵已经避免了四环,那么我们在选取子矩阵的时候在不打乱原来结构的情况下就可以避免H中的四环。如图2所示,H1从BLOCK1中选取,H2从BLOCK2中选取,只需要保证H2的基矩阵的前12列从与H1相同的列中选取得到即可。于是我们构造的H矩阵的结构如图3所示。显然, H1、H2和H都是非正规QC-LDPC校验矩阵。

图2 校验矩阵H1和H2的选取示意图Fig.2 The diagram of the selection of the parity check matrix H1and H2

图3 校验矩阵H结构示意图Fig.3 The diagram of the parity check matrix H

5 基于双层Tanner图的QC-LDPC码联合迭代译码算法

5.1 QC-LDPC码编码协作系统双层Tanner图

LDPC码可以用Tanner图表示,将之推广到QC -LDPC码编码协作通信系统中,如图4所示。其中,第一层对应着码字序列c1的Tanner图,第二层对应着码字序列c2的Tanner图。

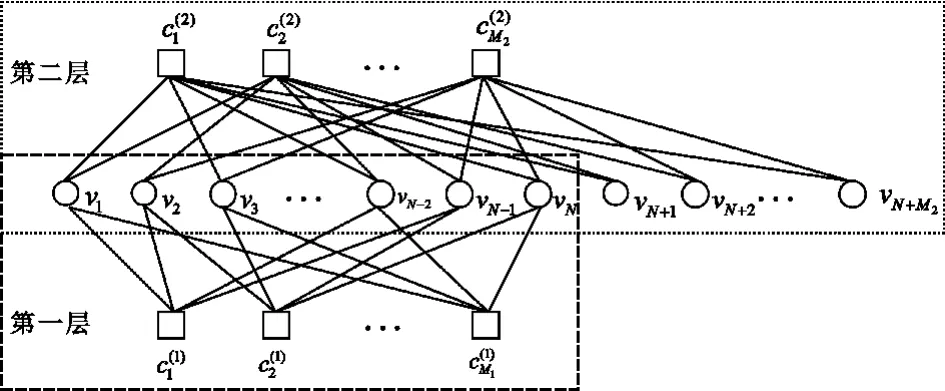
图4 QC-LDPC码编码协作通信系统双层Tanner图Fig.4 The double Tanner graph of QC-LDPC encoding cooperative communication system

在上面的双层Tanner图中,vn(n=1,2,…,N)同时参与了第一层和第二层的校验,即为H1和H2的共同变量节点;vn(n=N+1,N+2,…,N+M2)仅仅参与了第二层的校验,即仅为H2的变量节点。(k=1,2,…,M1)是第一层对应的校验节点,(k= 1,2,…,M2)是第二层对应的校验节点。这种协作通信双层Tanner图又称为联合Tanner图,其本质上仍然是一个Tanner图,将第二层的校验节点(k= 1,2,…,M2)转到第一层校验节点的右半部分,就可以等效为一个非正规的LDPC码对应的Tanner图。

5.2 联合迭代译码算法

我们将LDPC码的BP算法推广到协作通信系统中,于是提出了联合迭代译码算法。先介绍一下公式中使用的符号及其含义。

vn(n=1,2,…,N+M2)是变量节点集合;c(1)m(m =1,2,…,M1)和(m=1,2,…,M2)分别是第一层与第二层中的校验节点的集合;c(vn)是双层Tanner中变量节点vn参与的所有校验关系的集和; v()是与第一层校验节点或者第二层校验节点相关联的变量节点的总和;r=(r1,r2,…,rN, rN+1,…,rN+M2)是目的节点接收到的信息序列向量,其中前N个信息来自S-D信道,后M2个信息来自R-D信道。

准备阶段与初始化阶段详见文献[6]。注意,在BPSK调制中将1调制成-1,0调制成+1。

Step 1:校验节点信息处理(水平处理)

在校验节点处理过程中,双层Tanner中变量节点vn接收到的来自校验节点的信息如下式所示:

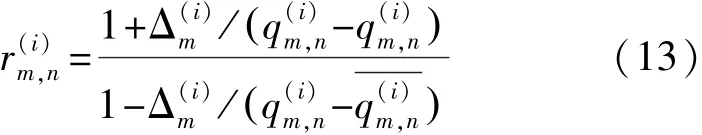
其中:

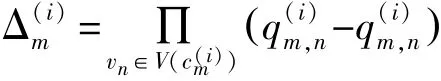
Step 2:变量节点信息处理(垂直处理)

在变量节点信息处理时,第一层Tanner图中第m个校验节点c(1)m接收到来自第n个变量节点的外信息表示如下:

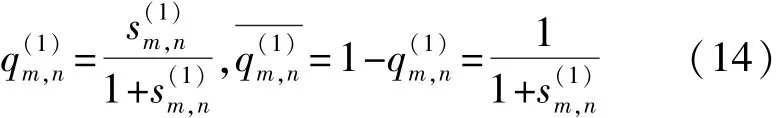
第二层Tanner图中第m个校验节点c(2)m接收到

Step 3:译码判决

重复步骤step1～3的迭代直至到达指定的迭代次数,计算出码字比特的后验概率为2

根据下述准则判决:

由以上处理过程可以看出,在双层Tanner图中第一层和第二层的处理完全相同,对变量节点的处理过程实质上等效于利用校验矩阵H迭代更新。

在仿真时,因为两层都是非正规QC-LDPC码,于是在Tanner图上进行分层迭代译码比利用H迭代译码方便很多。

6 QC-LDPC编码中继协作系统性能模拟

本节通过数值仿真研究了基于联合迭代译码算法的QC-LDPC编码中继协作系统的性能。假设协作系统中的信道相互独立且都是平坦瑞利慢衰落信道,仿真中采用BPSK调制,噪声采用均值为0、方差为1的高斯白噪声。

6.1 理想中继协作系统性能模拟

理想编码协作系统中,S-R信道理想为无差错传输。为了凸显中继编码协作系统的优越性,而且中继节点至目的节点的距离较源节点至目的节点的距离较短,故假设中继到目的节点的信道信噪比比源到目的节点的信噪比高1 dB,写成表达式形式: SNRR-D=SNRS-D+1,源节点至中继节点实现无差错传输。信源节点处采用校验矩阵H1编码,中继节点处采用校验矩阵H2编码。

由图5可以看出,随着R-D信道和S-R信道的信噪比的提高,误码率呈现对数式下降,且误码率在10-5时,在2、3、5这3种迭代次数中,理想协作系统相对于非协作系统分别有1.1 dB、1.5 dB和1.3 dB的性能优势,表明协作系统能够有效地提高系统的增益,这归功于联合迭代译码算法的使用。

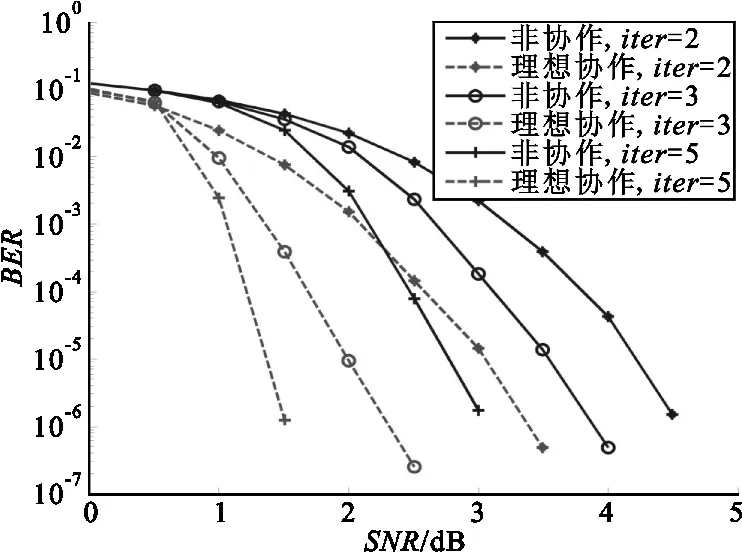
图5 非协作和理想协作系统的性能比较Fig.5 The performance comparison of non-cooperative and ideal cooperation systems

6.2 非理想中继协作系统性能模拟

考虑到源到中继节点的S-R信道不可能实现无差错传输,因此这部分内容主要研究两种非理想的情形:SNRS-R=SNRS-D、SNRR-D=SNRS-R+1时理想与非理想协作系统的性能比较;SNRS-R恒定,SNRR-D=SNRS-D时协作与非协作系统的性能比较。

6.2.1 情形1

由图6可知,源到中继节点和源到目的节点的噪声功率相同时,理想协作系统明显好于非理想协作系统的性能,这是由于中继节点编码后传递给目的节点的校验位存在错误,使得这部分外信息影响了整个系统的性能。可以看出,误码率为10-5时,迭代2次时理想仅比非理想协作性能好0.2 dB,迭代3次和5次时理想比非理想协作性能分别高0.8 dB和1 dB,这归功于中继节点处译出码字的错误减少。

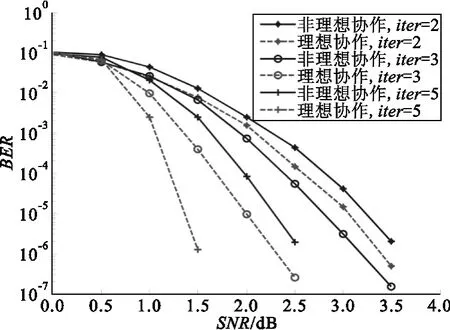
图6 非理想协作和理想协作系统的性能比较Fig.6 The performance comparison between non-ideal system and ideal cooperation system

6.2.2 情形2

图7(横坐标为源到目的节点的信噪比)表明,随着固定的SNRS-R的提高,在相同的迭代次数下非理想协作系统的性能越好,此情形适用于源节点和中继节点位置相对不变的情况。从图中可以看出,在SNR=3 dB和SNR=4.5 dB时,非协作系统的性能和非理想协作系统的性能出现了交叉,这是由于源到中继的链路的信噪比恒定,当源到目的节点链路的信噪比高于SNRS-R时,采用协作的效果将使得接收端的误码率反而不如非协作系统。图7中还仿真了按文献[6]构造的H1(2000,2,8)和H2(4000, 3,6)的系统非规则码构成的LDPC码编码协作通信系统,可知SNRS-R=3 dB,迭代次数为2,误码率为10-5时,该系统与本文中的系统的性能差0.2 dB,而且本文中的系统更易于硬件实现。

图7 非协作和非理想协作系统的性能比较Fig.4 The performance comparison between non-cooperation system and non-ideal cooperation system

7 结束语

本文提出了QC-LDPC码编码协作通信方式,利用基于有限域加群的构造方法构造出了满足满秩和高斯消元时不对校验矩阵中信息位部分的列作交换条件的检验矩阵,并得到了相对应的双层Tanner图及其高效联合迭代译码算法。数据分析表明,源到中继节点链路的可靠性对协作系统的性能影响较大。本文中的联合迭代译码算法可推广至多中继协作系统,使得系统的性能提升更明显;另外,基于QC -LDPC码编码协作通信系统具有硬件实现简单和消耗资源低等优点,可应用于通信系统中。

[1] Janani M,Hedayat A,Hunter T E.Coded cooperation in wireless communications:space-time transmission and iterative decoding[J].IEEE Transactions on Signal Processing,2004,52(2):362-371.

[2] Li Chuxiang,Yue Guosen,Khojastepour M A.LDPC-coded Cooperative Relay Systems:Performance Analysis and Code Design[J].IEEE Transactions on Communications,2008,56(3):485-496.

[3] Hunter T E,Nosratinia A.Cooperation diversity through coding[C]//Proceedings of 2002 IEEE International Symposium on Information Theory.Switzerland:IEEE, 2002:197-198.

[4] Hunter T E,Nosratinia A.Diversity through coded cooperation[J].IEEE Transactions on Wireless Communication,2006,5(2):283-289.

[5] Razaghi P,Yu W.Bilayer low-density parity-check codes for decode-and-forward in relay channels[J]. IEEE Transactions on Information Theory,2007,53 (10):3723-3739.

[6] Chen J,Yang F,Luo L,et al.Joint iterative decoding for simple-encoding systematic irregular LDPC based coded cooperation in non-ideal relay channel[J].Journal of Electronics(China),2010,27(3):305-315.

[7] Kschischang F R,Frey B J,Loeliger H A.Factor graphs and the sum-product algorithm[J].IEEE Transactions on Information Theory,2001 47(2):498-519.

[8] 刘原华,张美玲.一种可快速编码的QC-LDPC码构造新方法[J].电讯技术,2013,53(1):51-55.

LIU Yuan-hua,ZHANG Mei-ling.A New Design Mrthod For Quasi-cyclic LDPC Codes with Fast Encoding Ability [J].Telecommunication Engineering,2013,53(1):51-55.(in Chinese)

[9] Lan L,Zeng L,Tai Y Y,et al.Construction of quasicyclic LDPC codes for AWGN and binary erasure channels:A finite field approach[J].IEEE Transactions on Information Theory,2007,53(7):2429-2458.

CHENG Hao was born in Dongtai,Jiangsu Province,in 1989.He received the B.S.degree in 2011.He is now a graduate student.His research concerns channel coding theory and its application.

Email:ydxxch@163.com

仰枫帆(1966—),男,江苏南京人,分别于1993年和1997年获西北工业大学工学硕士学位和东南大学通信与信息系统专业工学博士学位,现为教授、博士生导师,主要研究方向为网络信息论和信道编码技术、无线通信中的信号处理技术和代数几何码等。

YANG Feng-fan was born in Nanjing,Jiangsu Province,in 1966.He received the M.S.degree from Northwestern Polytechnical University and the Ph.D.degree from Southeast University in 1993 and 1997,respectively.He is now a professor and also the Ph.D.supervisor.His research concerns network information theory and channel coding technology,wireless communication signal processing technology and algebraic geometry codes.

Email:yffee@nuaa.edu.cn

Finite Field QC-LDPC-based Encoding Cooperative System and its Joint Iterative Decoding Technology

CHENG Hao,YANG Feng-fan

(College of Electronic Information Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)

To improve the performance of a communication system and push project realization,the QC-LDPC code based on the additive group of finite field is presented and through a special method,a full rank QC-LDPC(Quasi-cyclic Low-Density Parity-Check)code is constructed and used in coding cooperative communication systems at the source node and the relay node.Thus a general check matrix is constructed. Then the double Tanner graph is derived and the joint iterative decoding algorithm is adopted based on the double Tanner graph at the destination node.Simulation results show that,when BER=10-4and iteration times is 5,the ideal cooperative communication system performance is better than the non-cooperative and non-ideal cooperative systems for 1.2 dB and 0.8 dB;When the SNR for S-D equals that for R-D,the signal-to-noise ratio(SNR)of S-R channel rises,and the non-ideal cooperative communication system performance becomes better.

cooperative communication system;additive group of finite field;QC-LDPC;double Tanner graph;joint iterative decoding algorithm

The National Aeronautical Science Foundation of China(No.20105552031)

date:2013-07-31;Revised date:2013-11-19

航空科学基金项目(20105552031)

**通讯作者:ydxxch@163.com Corresponding author:ydxxch@163.com

TN911.22

:1001-893X(2013)12-1574-06