具有时滞和的离散系统的稳定性分析
2013-06-23焦建民
焦建民
(宝鸡文理学院 数学系,陕西 宝鸡 721013)
时滞现象广泛存在于各类实际系统之中,是引起系统不稳定和性能变差的重要因素,因此,对于时滞系统的研究一直是控制领域的研究热点,并取得了许多研究成果。如文献[1-2]和[3-6]分别研究了连续时滞系统和离散时滞系统的稳定性问题,给出了系统一些稳定性条件。文献[1-6]所考虑的系统中,状态时滞是一种单一的形式,文献[7]指出:在一些实际问题中,如网络控制系统,信号从一点传输到另一点,可能要经过一些网络节点,这些节点在网络传输过程中会导致具有不同特性的时滞出现,这些时滞不能合并在一起进行研究。因此,文献[7]提出了具有时滞和的系统,并给出了系统的一个稳定性准则。文献[8-10]进一步改进了文献[7]的结果,给出了一些保守性更小的稳定性条件。然而,文献[7-10]所考虑的系统均为具有时滞和的连续系统,对具有时滞和的离散系统,相关研究成果还很少见。本文针对具有时滞和的离散系统,基本Lyapunov稳定性理论,应用线性矩阵不等式(LMI)处理方法,研究了系统的稳定性问题,给出了系统新的稳定性准则,并利用仿真实例验证了所给结果的有效性。
本文采用以下记号:对实对称矩阵X和Y,X≥Y(X>Y)表示X-Y为半正定(正定)矩阵;AT表示矩阵A的转置;“*”表示对称矩阵的主对角线以上块矩阵的转置矩阵;I和O分别表示适当维数的单位矩阵和零矩阵。
1 问题描述
考虑如下具有时滞和的离散系统:

其中,x(k)∈R″为系统状态;φ(k)系统初始条件;A,B为已知适当维数的常数矩阵;d1(k),d2(k)表示系统时变时滞,满足:

其中,d1,d2为已知正整数。为叙述方便,后文记:

引理1[3]给定矩阵R>0,正整数d2≥d1>0及向量函数x:[d1,d2]→Rn,下面的不等式成立:
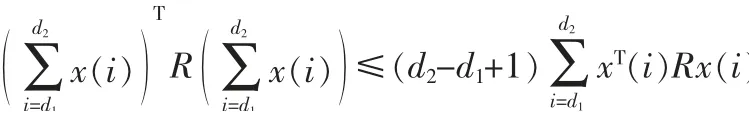
2 主要结果
定理1给定正整数d2≥d1>0,对满足(2)的时变时滞d1(k),d2(k),系统(1)是稳定的充分条件是,存在适当维数的矩 阵P>0,Q1>0,Q2>0,Q3>0,R>0及M1,M2,M3,使 得 下 面 的LMIs(3)和(4)成立:


3 数值实例
考虑离散时滞系统(1),设其系数矩阵为:
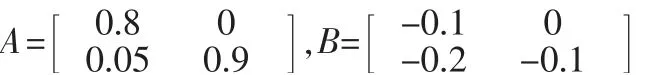
当给定时滞d1(k)上界d1=10,应用定理1可得,使得系统(1)满足稳定的时滞d2(k)上界d2的最大值为7;类似的,当给定时滞d2(k)上界d2=5,应用定理1可得,使得系统(1)满足稳定的时滞d1(k)上界d1的最大值为12,可以看出,本文的定理1是有效的。
4 结束语
文中针对一类具有时滞和的离散系统,通过构造合理的Lyapunov泛函,并保留了Lyapunov泛函差分中的有用信息,得到了基于LMI的时滞相关稳定性充分条件,并应用数值算例验证了所得到的有效性、可行性,为具有时滞和的离散系统控制问题的进一步研究提供了参考。
[1]HE Yong,WANG Qing-guo,LIN Chong,et al.Delay-rangedependent stability for systems with time-varying delay[J].Automatica,2007,43(2):371-376.
[2]Park P G,Ko J W,Jeong C.Reciprocally convex approach to stability of systems with time-varying delays[J].Automatica,2011,47(1):235-238.
[3]GAO Hui-jun,CHEN Tong-wen.New results on stability of discrete-time systems with time-varying state delays[J].IEEE Transactions on Automatic Control,2007,52(2):328-334.
[4]ZHANG Bao-yong,XU Sheng-yuan,ZOU Yun.Improved stability criterion and its applications in delayed controller design for discrete-time systems[J].Automatica,2008,44(11):2963-2967.
[5]FANG Mei.Delay-dependent stability analysis for discrete singular systems with time-varying delays[J].Acta Automatica Sinica,2010,36(5):751-755.
[6]JIAO Jian-min.Robust stability and stabilization of discrete singular systems with interval time-varying delay and linear fractional uncertainty[J].Internal Journal of Automation and Computing,2012,9(1):8-15.
[7]Lam J,GAO Hui-jun,WANG Chang-hong.Stability analysis for continuous systems with two additive time-varying delay components.System and Control Letters,2007,56(1):16-24.
[8]Dey R,Ray G,Ghosh S,et al.Stability analysis for continous systems with additive time-varying delay:a less conservative results[J].Applied Mathematics and Computation,2010,215(10):3740-3745.
[9]Hamed B,Chaabane M,Kalem W.Absolute stability of nonlinear systems with two additive time-varying delay components[J].Internal Journal of Automation and Computing,2011,8(4):391-402.
[10]SHAO Han-yong,HAN Qing-long.On stabilization for systems with two additive time-varying input delays arising form networked control systems[J].Journal of The Franklin Institute,2012,349(6):2033-2046.
