一种基于子带GSC的语音增强算法

邓俊杰，孙 超

（西北工业大学 航海学院，陕西 西安 710072）

近几十年来，语音增强技术得到了广泛研究和发展。然而，直到今天，在实际声场环境中，降低噪声级、提高语音能懂度，仍然是一项富有挑战性的任务。

基于麦克风阵列的语音增强技术，充分利用了信号的空域信息，相比仅利用信号时域信息的单通道语音增强算法，能获得令人更加满意的改善效果，被广泛应用于电视电话会议、语音识别、语音增强、助听器等设备中。迄今为止，人们已经提出了许多基于麦克风阵列的语音增强算法，典型的如延时-求和波束形成、最小方差无失真响应（MVDR）波束形成、自适应波束形成（ABF）等。在众多算法中，Griffiths–Jim于1982年提出的广义旁瓣相消器（GJGSC）[1]，因其结构简单、易于实现，成为了自适应波束形成中最经典也是目前使用最广泛的一种语音增强算法。

但是，GJGSC也有其缺点。其一，它能够有效消除相干噪声，对非相干噪声（如高斯白噪声）或弱相关噪声（如散射噪声）却无能为力。为此，Zelinski[2]提出基于维纳（Wiener）滤波的多通道后置滤波器，Marro等人[3]对Zelinski后置滤波器进行了深入研究，指出该滤波器的传输函数可由输入信号的自相关和互相关功率谱获得，从而使得Zelinski后置滤波器在多通道语音增强中得到普遍运用；其二，GJGSC往存在语音信号对消现象，即产生了语音泄漏，人们为此提出了多种稳健算法[4]，改善了GSC在实际应用中的性能。

文中将DFT调制子带滤波器组同GSC相结合对语音信号进行子带滤波，不仅可以降低运算量并且可以获得更好的去噪效果。同时，算法将噪声相关函数应用于Wiener后置滤波器，从而更加有效地去除了GSC输出语音中残留的噪声。文中首先简单介绍了麦克风阵列中广泛采用的广义旁瓣器（GSC）以及基于DFT调制子带滤波器组，随后对本文所提的语音增强算法作了较为详细的叙述，最后以实验数据对该算法进行测试，并得出结论。

1 子带滤波器

图1 所示为子带滤波器组的结构框图，Hk（z）=0，1，…，K－1称为分析滤波器组，Gk（z）=0，1，…K－1 称为合成滤波器组，↑D和↓D分别是上、下采样器。因为存在采样率的变化，子带滤波器组也称为多速率数字滤波器组。

子带滤波的基本思想是将输入的全带信号进行频带划分，得到位于不同频带上的子带信号，对其下采样后再进行子带滤波处理，最后对滤波后的信号上采样并进行子带信号重构。对于一个自适应滤波算法，设全带滤波完成一次迭代的运算量为 o（lp）或 o（lp2），由于以较低的速度更新较少的系数，相应的子带滤波运算量为全带的K/D2或K/D3其中，lp为滤波器长度。

图1 子带滤波器结构框图Fig.1 Sub-band filter structur

文献[5]提出了一种基于DFT调制滤波器组的高效实现算法，该算法在允许滤器组存在相位畸变的前提下，通过独立地最小化各个混迭成份的幅度，从而使得混迭畸变达到最小。根据该算法，得到如图2所示的子带分析滤波器组的幅频响应。其参数设置如下：滤波器长度lp=128，子带数K=16，采样因子D=8。由图可知，经该方法得到的滤波器组具有相同的主瓣级，且用较少的滤波器抽头数，即可达到较低的旁瓣级（低于-80 dB）。另外，文献[10]已经证明，由该方法得到的分析－合成滤波器组处理后信号其畸变量（包括混叠畸变、幅度畸变和相位畸变）将能够得到有效的控制和降低。

图2 分析滤波器组幅频响应Fig.2 Amplitude-frequency response of the analysis filter bank

2 基于子带GSC的语音增强

基于收敛速度和去噪效果的考虑，本文提出了的基于子带GSC的语音增强算法，其原理如图3所示。将固定波束形成器（FBF）和阻塞矩阵（BM）的输出进行子带分解，然后将下采样后的子带信号送入自适应噪声对消器（ANC）进行子带滤波，最后将处理后的信号上采样后通过子带合成滤波器，得到增强后的语音。为了去除增强后语音中的非相干噪声成份，提高语音质量，框图中加入了Wiener后置滤波器。同时，为了降低增强后语音的失真，算法中加入语音活性检测（VAD）用来标识语音帧的成份类型，并仅在噪声帧（VAD=0）时执行Wiener后置滤波。

设由M个麦克风组成的均匀线列阵接收到的语音信号经延时估计和补偿后为 xm（n），m=0，1，…，M-1，GSC 的主输入采用简单波束形成方法：

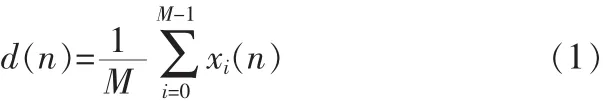
BM的输出为：

图3 系统框图Fig.3 System structure

将 d（n）和 b（n）进行子带分解后的信号，分别作为ANC的主输入和参考输入，通过自适应滤波算法，从主输出中减去与参考输入相关的成份，则可得到增强后的子带语音信号。

考虑到BM信号存在语音泄漏，采用传统LMS算法的GSC（GJGSC）将在语音输出端产生失真，且泄漏越多，失真越大。本文采用范数约束自适应滤波（NCAF）算法[4]，该算法通过对ANC的权值系数向量二范数进行约束，可以有效减小目标语音的对消发生，降低增强后语音的失真度。

令 dk（n）和 uk，m（n）分别为 d（n）和 b（n）经分解得到的子带信号（k=0，1，…，K-1，m=0，1，…，M-2）。 则第 k 个 ANC 第 i次迭代的输出为：

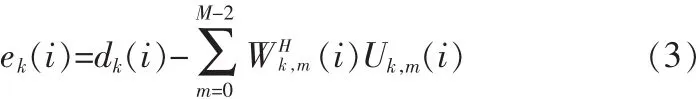
L为ANC抽头个数

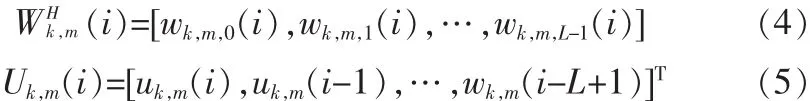
NCAF的权值迭代公式为：

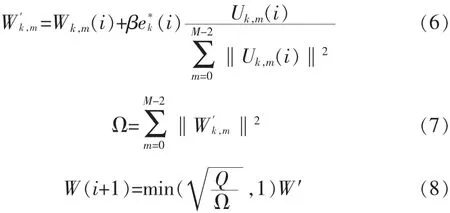
β为迭代步长，Q为一阈值常数。

传统的多通道Wiener滤波器，假定声场环境为非相干噪声场，这种情况在实际中很少遇到。文中将噪声相干函数引入Wiener滤波器中，能够更加有效去除经GSC滤波后语音中的残留噪声。

通道 i和 j（i≠j）之（间的噪声相干函数定义为[6]：

假定语音和噪声不相关，且语音和噪声在各通道上的自谱密度相等，则可得下式：

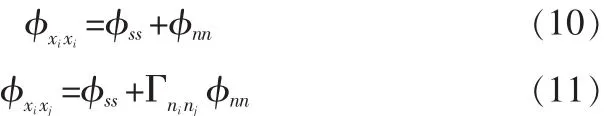
从以上两式可得语音自谱密度的估计值为：

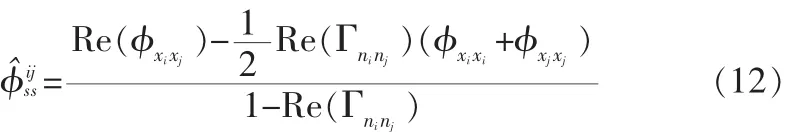
将φˆss代入Wiener滤波器表达式中，可得滤波器传输函数为：

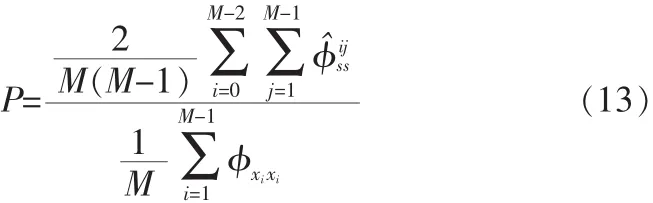
为了测量噪声相干函数，算法中加入了语音活性检测（VAD）[7]，并仅在噪声帧（VAD=0）执行后置滤波操作，后置滤波仅在噪声帧进行也可以减少增强后语音的失真。

3 实验仿真

文中仿真数据取自卡内基·梅隆大学（CMU）实测麦克风阵列语音数据库[8]，该语音库使用由15个麦克风组成的线性嵌套式阵列，其中8号阵元为整个阵列的对称中心，声源即位于该阵元的正前方。该嵌套阵列排列方式为（假定阵元最小间距为d，9-16号阵元的排列方式可由对称得知）：1、2号阵元间距为 4d，2、3、4号阵元间距为2d，4-8号阵元间距为d。录音在一嘈杂的实验室内进行，为了获取参考语音，一头戴式麦克风位于声源近点。麦克风阵列选用由第5-11号阵元所组成的标准线列阵，并使用数据库中的an101-mtmsarrC3A组语音数据，声源到阵列中心的距离为3 m，阵元间距4 cm，数据采样率为16 kHz。参考语音与8号阵元上的语音波形如图5所示。

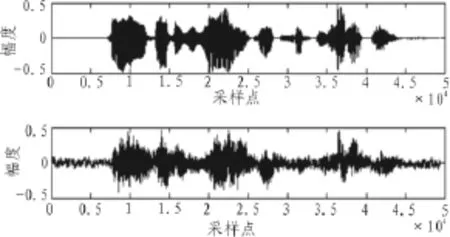
图4 参考语音与加噪语音波形图Fig.4 Reference speech and noisy speech

采用分段信噪比（SegSNR）来评价语音的客观质量，它可以衡量语音时域波形的失真程度，其与主观测试之间的相关系数为0.77，远高于一般信噪比的相关系数0.24。经计算，加噪语音的SegSNR约7.124 7 dB。

图5为采全带GSC与子带GSC增强后语音的波形图，经全带GSC增强后语音的SegSNR为12.669 4 dB，经子带增强后语音的SegSNR为13.694 8 dB，SegSNR提高了1 dB。仿真中，基于全带的GSC经过大约2000次收敛，而基于子带的GSC经过1000次就已收敛，收敛速度提高了一倍。

图5 全带GSC与子带GSC增强后语音波形Fig.5 Enhanced speech with full band GSC and sub-band GSC

图6为采用Zelinski后置滤波器与使用文中所用后置滤波器增强后语音的波形图，其分别SegSNR为13.917 3 dB和16.951 8 dB，SegSNR获得了3 dB提升。若噪声的为已知，即Γ已知，则其改善将得到进一步提升。

图6 不同后置滤波器时增强语音波形Fig.6 Enhanced speech with different pos-filter

4 结束语

文中提出了一种基于子带滤波的GSC语音增强算法，并应用了改进的Wiener后置滤波方法，达到更好的去噪效果。在噪声场未知时，需通过VAD检测并仅在噪声帧内进行Wiener后置滤波，故此时算法在很大程度上依赖于VAD的检测精度（精度越低则增强后语音失真越大）。在实际声场中（比如室内环境），一般可以先在没有语音的情况下获得噪声相干函数，然后运用此算法进行语音增强。此时，则不再需要VAD检测并且能够得到更好去噪效果。

[1]Griffiths L J，Jim C W.An alternative approach to linearly constrained adaptive beamforming[J].IEEE Bans.Antennas Propag，1982（30）:27-34.

[2]Zelinski R.A microphone array with adaptive post-filtering for noise reduction in reverberant rooms[J].Proc.of ICASSP-88，1988（5）:2578-2581.

[3]Marro C C，Mahieux Y Y，Simmer K U，et al.Analysis of noise reduction and dereverberation techniques based on microphone arrays with postfiltering[J].IEEE Trans.Speech Audio Process，1998（6）:240-259.

[4]Hoshuyama O，Sugiyama A，Hirano A.A robust adaptive beamformer for microphone arrays with a blocking matrix using constrained adaptive filters[J].Signal Processing，IEEE Transactionson，1999，47（10）:2677-2684.

[5]de Haan，J M，Grbic N，et al.Filter bank design for subband adaptive microphone arrays[J].Speech and Audio Processing，IEEE Transactions，2003，11（1）:14-23.

[6]McCowan I A，Bourlard H.Microphone array post-filter based onnoisefieldcoherence[J].SpeechandAudioProcessing，IEEE Transactions，2003，11（6）:709-716.

[7]王月，曲百达，李金宝，等.一种改进的基于频带方差的端点检测算法 [C]//中国控制与决策学术年会论文集，2007：301-303.

[8]Tom Sullivan.CMU Microphon array Database[EB/OL].（1996）.Http://www.speech.cs.cmu.edu/databases/micarray/cmu_tms_multimic.tar.gz.