时效约束的高强度快递需求区域车辆调度模型＊

戢晓峰 陈 方 覃文文 肖俊奇

（昆明理工大学交通工程学院1） 昆明 650500） （昆明理工大学社会科学学院2） 昆明 650500）

为了提高快件集散的时效性，快递企业必须减少收派员往返于客户与点部之间的时间，此时就引进了“移动仓库”的概念.移动仓库又称“汽车二程接驳”，就是在收、派量大且稳定的区域，租赁场地建立一个或多个“前沿”交接中转站，配合IVCO 货车的循环流动，节省单个收派员往返于客户与点部之间的时间，相应延长在客户处的服务时间［1］.在此背景下，高强度快递需求区域的快递车辆调度，直接关系到整个收派件过程的效率、快递成本以及顾客满意度，并将会对企业的运营效益产生重要影响.本文针对高强度快递需求区域的车辆调度问题，考虑收派件时效约束与移动仓库容量，建立了有时限的混装卸车辆调度模型，最大限度利用车辆载重量，以保证快递系统的高效运营，提高快递服务水平.

1 问题描述

快件收派配送是快递企业进行客户服务的直接手段和重要环节，车辆调度的合理与否对配送速度、运营成本及经济效益均会产生很大影响［2］.高强度快递需求区域的车辆调度问题本质上是一个车辆优化调度问题（vehicle scheduling problem，VSP），即一个典型的NP 难题.高强度快递需求区域的某个点部中心向n个移动仓库进行收派件，每个工作日共有3批派件进港，要求在下一批派件进港前必须完成上一批的派件任务，每个工作日必须完成上午与下午两个时段的收件任务，且上时段的任务必须在下时段来临前完成，否则会降低时效性或导致移动仓库爆满.求满足上述时间限制、车辆容量限制、移动仓库容量限制且费用最少的车辆行驶路线，即为带时间窗的车辆调度问题.由于收派件任务必须在要求的时间范围内完成，若超出这个时间范围，则得到的解为不可行解，即必须满足时间窗约束，因此为带硬时间窗的车辆路径问题.本文在国内外VSP研究成果的基础上，提出适合高强度快递需求区域车辆调度问题模型的目标函数和约束条件，通过构造时间窗检查约束条件，求解有硬时间窗的VSP.

1）车辆调动建模的条件界定 （1）以一个点部中心为源点，且只有一个源点，即单源点.区域收派件货车从此中心发出，经各移动仓库，最后回到此中心；（2）点部中心拥有k 辆相同的厢式货车来完成点部区域的收派件工作，且每公里成本（包括耗油量及人力成本）相同；（3）根据收派件任务的特点，每天必须在相应四个时段完成四批派件进港任务，在两个大时段内必须完成相应时段所有移动仓库积累的收件任务；（4）每个移动仓库管辖的范围固定不变 且移动仓库的货物存放遵循先进先出的原则；（5）所有快件以标准件进行计算，即以件为单位来计量仓库容量、快件需求量、车辆最大载重量、剩余载重量、装载量、派件量与收件量.

2 车辆调度模型建立

1）系统初始化 令eit＝0，即在工作日开始令每个移动仓库的库存量为0.

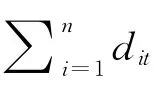
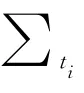
4）车辆的行车路线的确定 每批派件任务采用相同的车型，且车辆的最大载重量为Q，货车的数量没有限制.每辆车派件运行时间需要满足的时间条件为

3 车辆路线求解

针对车辆路线问题采用节约里程法求解，综合考虑路线距离和时间因素，如服务需求稳定且配送时间固定，可采用中间指标：路程长度／平均车速；结合快件服务需求特点及收派件实际流程，可采用指标：路程长度／平均车速＋每个节点的停留时间即收派件的装卸货时间.

如图1所示，点部中心0向第1－n个移动仓库派件，Pαi为第α 批第i 个移动仓库的派件量，件：ti为每个移动仓库的装卸货时间；t0i为点部中心0与第i个移动仓库之间的最短运行时间；tij为移动仓库之间的最短运行时间，h.

图1 点部与移动仓库路径分布车辆路线求解步骤如下.

步骤1 计算点部中心至各移动仓库以及各移动仓库之间的最短作业时间（包括运行时间和装卸货时间），如表1所列.

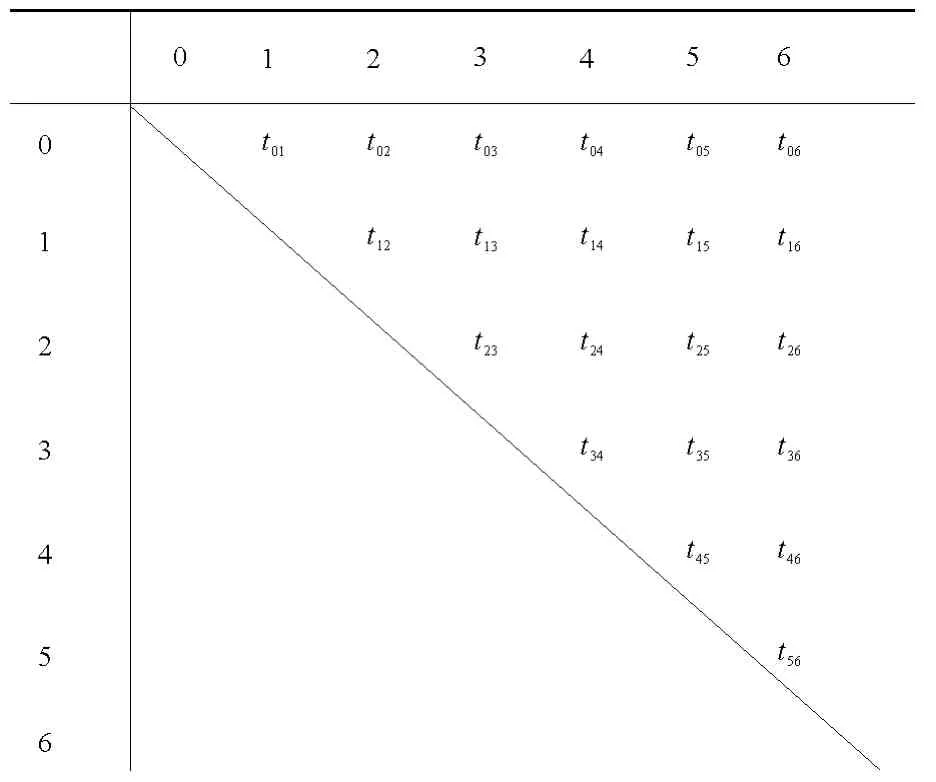
表1 最短时间表

步骤2 由上述最短作业时间计算出由点部中心0到各移动仓库之间的节约时间，并得到节约时间表2（节约时间为负数时，无实际意义，为0），根据节约里程法的基本原理：三角形一边之长必定小于另外两边之和，则节约里程Sij＝D0i＋D0j－Dij，如图2所示（i，j 表示移动仓库）.根据快递收派件的具体流程，得到节约时间为

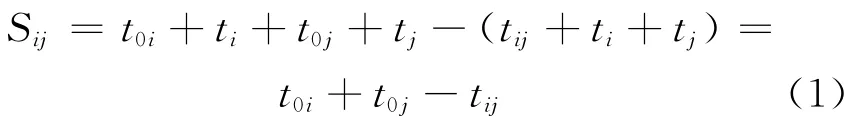
表2 节约时间表

步骤3 根据节约时间多少的顺序，编制节约时间顺序表，以便使得节约时间最多的移动仓库组合装车完成收派件任务.

图2 节约里程法的基本原理

步骤4 根据节约时间顺序表和配车约束（车辆最大载重量限制）、车辆收派件的间限制等约束条件，即

Wk＝∑Pαi≤Q 且ETα≤Si≤LTα且∑（t0i＋tij＋tj0）＋∑ti≤LTα－ETα，得到每辆车的派件路径以及装载货物的分配.由此，得到每一条派件路径后从集合Cαi剔除该次循环 点，进行第二次路径选择，并进行循环.

步骤5 将Cαi中剩余无法分配的点在满足时间条件：ETα≤Si≤LTα且∑（t0i＋tij＋tj0）＋∑ti≤LTα－ETα的前提下，分配到WK＜Q 的车辆，使得车辆的利用率达到最大.如果有剩余派件量，单独派车来完成，最后分配成为x 个组.

4 车辆调度模型优化

1）车辆数k的确定 将以上x 个组合中对应的收派件任务完成时间进行分析，并重新进行二次分组，形成了y 个组合，这些组合的收派件任务完成的作业时间积累量均满足t≤LTα－ETα，单独遗留下z 个组合不能重新进行二次分组，则需要的车辆数k＝y＋z.

2）发车时间的安排 从车场调度出来的k辆车同时发车.针对上述的y 辆车，每辆车根据所派送的任务中对应的移动仓库的优先度积累量进行比较，按照从大到小的顺序依次进行派送，同一辆车根据它的配送任务进行连续发车，直到任务完成，则停止发车.

3）进行派件任务时的收件量分配情况，若0≤dit≤Yαki，则Sαki＝dit；若dit＞Yαki，则Sαki＝Yαki.

若收派件任务完成后，车辆仍有剩余载重量且下一刻没有派件任务，则在满足时间限制ETα≤Si≤LTα且∑（t0i＋tij＋tj0）＋∑ti≤LTα－ETα的条件 下，加入其他移动仓库，进行单独收件，使得车辆的利用率达到最大.

需要指出的是，对于以上调度车辆，在完成派件任务后，在下一批派件任务来临之前，启动单独收件任务管理机制.要求必须在两个时刻T1，T2前完成对应的两个时段的收件积累量，每天收派员的最早工作时间为T0.

5 基于移动仓库优先度的路径优化

鉴于移动仓库服务能力的限制，需要考虑移动仓库的优先度问题，以防止出现仓库爆满现象，本文按照优先度从高到低的顺序得到路径，方法简述如下

1）当每个移动仓库的优先度eit均不相等时，按优先度排列顺序进行相应仓库快件的收取.

2）当存在两个以上的移动仓库的优先度相等时，设这些移动仓库组成的集合为C，针对这几个移动仓库按照基于Dijkstra算法来选择最优路径，使得目标函数满足：

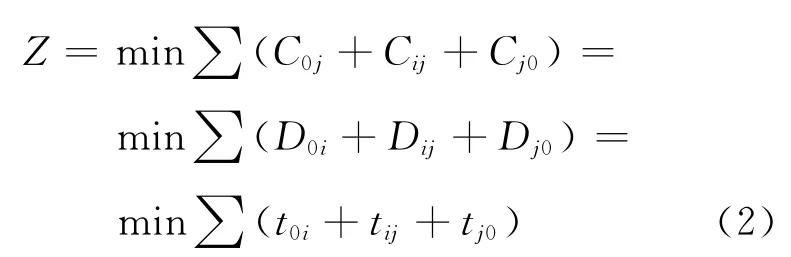
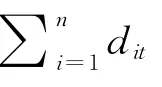
6 结束语

本文针对高强度快递需求区域车辆调度问题的实际需求，建立了有时限的混装卸车辆调度问题模型.通过构造时间窗检查约束条件，求解有硬时间窗的VSP.在解决问题的过程中，对节约里程算法进行适当了修正，基于Dijkstra算法进行路径优化，不但求得满足实际需求的可行解，而且还可分析剩余点对最终线路的影响，能够指导高强度快递需求区域建立移动仓库后的车辆调度实际问题.

［1］教育部高等学校物流类专业教学指导委员会.“SF杯”第三届全国大学生物流设计大赛案例［Z］.北京：教育部高等学校物流类专业教学指导委员会，2010.

［2］李 杰.基于网络的邮政运输车辆调度问题研究［D］.成都：西华大学，2009.

［3］陈晓伟，张悟移，耿继武.节约法在配送路线选择中的应用［J］.昆明理工大学学报：理工版，2003，28（4）：140－143.

［4］王宏勇，卢战伟.嵌入式GIS 最短路径分析中Dijkstra法改进［J］.测绘学院学报，2005，22（1）：43－45.