吴江学院路大桥钢混结合段应力分析
2013-06-19石雪飞
石雪飞 黄 力 阮 欣
(同济大学桥梁工程系 上海 200092)
0 引 言
近年来,随着我国交通基础设施大规模建设的兴起,混合梁斜拉桥建设得到快速发展[1].2010年建成的主跨达926m 的鄂东长江大桥和816m的荆岳长江大桥,均采用混合梁斜拉桥方案,相关研究探讨了其结合段简化计算方法以及合理构造等,积累了较为全面的研究成果.鄂东长江大桥和荆岳长江大桥均为超大跨径混合梁斜拉桥,虽研究成果具有普遍适用性,但对于中小跨径独塔混合梁斜拉桥,在受力和构造上均有所不同.因此,为研究基于中小跨径斜拉桥混合梁结合段的传力机理和构造形式,本文以吴江学院路大桥为例进行应力分析.
吴江市学院路跨京杭运河大桥采用123m+75m 独塔双索面斜拉桥方案,塔、梁、墩固结,边跨设置辅助墩.边跨和主跨距离桥塔中心线22.1m内为混凝土主梁,主跨其余部分设置为钢主梁.主桥主梁形式为分离式双边箱主梁,如图1所示为钢主梁1/2横断面示意图,图2为混凝土箱梁1/2横断面示意图.

图1 斜拉桥钢主梁横断面图(单位:mm)
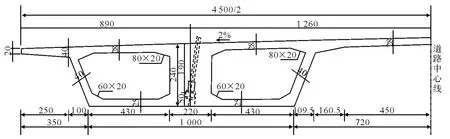
图2 斜拉桥混凝土主梁横断面图(单位:cm)
钢箱梁与混凝土箱梁结合位置选择在主跨第3号斜拉索锚固横梁处.如图3所示,结合段实体混凝土长度为1.5m,结合段钢箱梁套在预应力混凝土箱梁外侧,并与其浇注成为一体.箱梁顶、底板及端承压板通过开孔钢板、焊钉与混凝土梁体连接成整体,并利用混凝土梁内纵向预应力和结合段纵向劲性骨架形成弯矩的传递.通过端承压板紧贴在混合段钢横梁端面上传递轴向力[2].梁中剪力通过开孔板中混凝土抗剪得到传递.2种梁体在结合段和钢箱梁间设置了过渡段,长度为4.6m,通过在钢箱梁上、下翼缘的U 形加劲肋上加焊T 肋并逐渐变高变宽,使结合段刚度突变得到缓解.
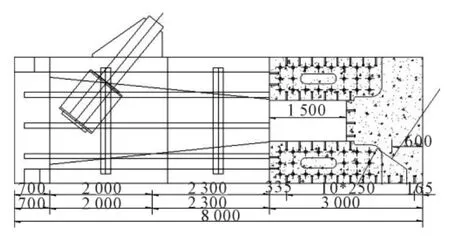
图3 钢混结合段构造图(单位:mm)
1 空间有限元数值计算
1.1 模型建立
本桥主梁钢混结合段共8m 长,为能真实模拟结合段最外侧两截面处受力情况,接近圣维南原理要求,实际建模中结合段分别向钢主梁侧延伸3m,向混凝土主梁侧延伸4.7m,计算模型全长15.7 m,如图4.结合段模型布置有2 对斜拉索,分别为WC3和WC4.

图4 结合段局部模型在整体模型中示意图(单位:m)
1.1.1 Miads模型 Midas空间杆系模型(见图5)考虑了恒载、活载、预应力、沉降、温度变化、收缩徐变作用.计算中根据规范对各种荷载工况进行组合,确定局部模型受力最不利荷载工况组合.
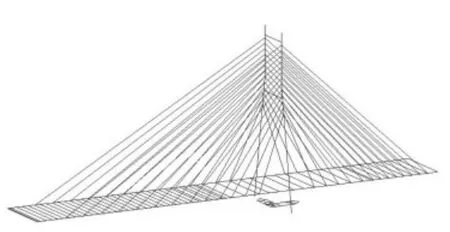
图5 Midas空间杆系模型
1.1.2 Ansys模型 先用大型通用有限元软件Ansys建立全桥双主梁杆系模型.主塔和主梁使用Beam188单元,拉索采用Link8 单元.横梁使用Beam4单元,按实桥位置输入,横梁刚度取实桥等效刚度.
再利用Ansys建立钢混结合段局部实体模型(见图6),采用Shell63壳单元模拟钢箱梁顶、底板及相关加劲肋、横隔板等;采用Solid45单元模拟混凝土箱梁及相关混凝土横隔板、横梁;采用Link8[3]单元模拟梁体纵向、横向预应力钢束和斜拉索.预应力和斜拉索索力采用附初应变方法施加.

图6 钢混结合段实体模型示意图
最后将钢混结合段局部实体模型接入对应Ansys空间杆系模型中,以钢混结合段结合面为控制断面,利用Midas空间模型得到各最不利工况组合与活载的影响线加载位置,进行数值计算.图7为钢混结合段实体模型在全桥杆系模型中的计算示意图.
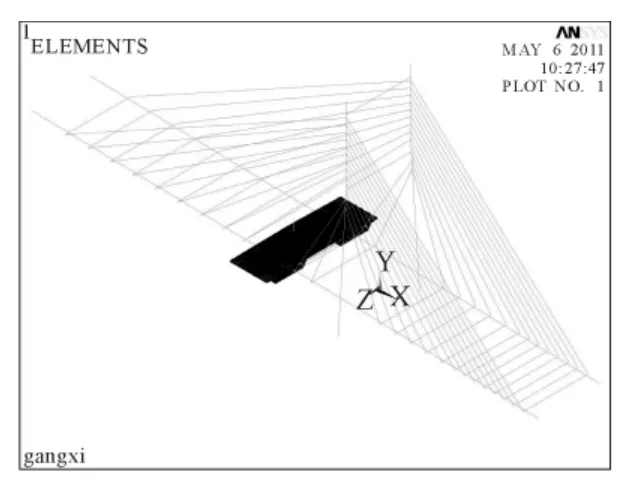
图7 钢混结合段在全桥模型中位置示意图
1.2 计算假定及荷载作用
1.2.1 计算假定 (1)钢混结合段局部实体模型中假定钢主梁与混凝土之间采用刚性连接.为验证此假定,建立考虑剪力钉、开孔板等构造钢格式精细化模型(见图8)[4],由计算结果可知钢与混凝土之间相对位移在73μm 以下,故在整体模型计算中假定没有相对滑移前提是成立,受篇幅限制略去详细计算结果;(2)计算的各最不利工况组合及活载加载影响线位置取自Midas空间杆系模型结构分析结果.
1.2.2 荷载作用 计算模型中考虑恒载、汽车活载、预应力作用、基础沉降、整体温度变化作用、钢混结合段混凝土收缩、徐变效应、钢混结合段梯度非线性温度.
1.3 作用工况
钢混结合段最不利受力状态考虑了施工阶段和成桥阶段两种状态,以结合面为控制断面,运用Midas空间杆系模型进行分析.得出在全桥整体计算中的四种最不利工况荷载组合:(1)结合面最大轴力工况;(2)结合面最大正弯矩工况;(3)结合面最大负弯矩工况[5];(4)结合面最大剪力工况.再在ANSYS混合模型中按照上述荷载组合及影响线位置进行活载加载.

图8 钢格室精细化模型
1.4 边界条件
由于本研究是采用将钢混结合段实体模型接入全桥空间杆系模型中进行计算,不存在结合段边界条件问题.在杆系模型与结合段实体模型接入点处采用刚域方法进行连接.
2 计算结果与分析
2.1 结合段钢箱梁应力
钢混结合段总体应力水平如图9所示,分别为钢梁段纵桥向和Mises应力分布.在最大正弯矩工况下钢梁段纵桥向应力水平较低,结合段钢梁纵桥向正应力范围在40~90 MPa之间.钢混结合段钢梁Mises应力分布与纵桥向应力相近,应力水平一般在100 MPa以下,最大Mises应力为142 MPa,远小于其屈服应力[6].
2.2 结合段混凝土应力
钢混结合段混凝土纵桥向和横桥向正应力分布如图10,除斜拉索锚固区应力集中现象,其应力水平在-12~1.5MPa之间.在横向负弯矩作用下,结合段混凝土悬臂板根部有较小拉应力产生,建议增加横桥向预应力钢束.在斜腹板处由于预应力锚固存在明显应力集中现象.

图9 钢混结合段钢主梁应力云图

图10 钢混结合段混凝土应力云图
由图11可知,钢混结合段混凝土第一主应力范围在-1~1.5 MPa,在混凝土主梁斜腹板和左侧实心箱室处出现较大主拉应力,分别是由于该位置位于横向预应力锚固点与斜拉索锚固区处.结合段混凝土第三主压应力水平大致在-11~0 MPa范围内.

图11 钢混结合段混凝土主应力云图
3 结 论
1)钢混结合段在恒载及活载作用下传力明确可靠,构造合理.计算结果表明结合段钢梁各构件应力分布均匀,变形平顺;结合段混凝土应力变化平顺,应力扩散均匀.
2)利用有限元计算分析钢混结合段应力状态时,必须较准确模拟结合段边界条件与明确最不利荷载工况.可利用Midas建立全桥空间梁单元杆系模型,提供全桥内力值与各计算最不利工况影响线,确定最不利工况荷载加载大小与位置,再利用ANSYS混合模型较真实模拟局部模型实际边界条件.
3)钢混结合段局部实体模型计算中,以钢主梁与混凝土之间无滑移假设为前提.建立钢格室精细化模型,计算结果表明,在其最不利荷载作用下钢主梁与混凝土之间滑移非常小,可认为两者间无相对滑移.
[1]陈开利,余天庆,习 刚.混合梁斜拉桥的发展与展望[J].桥梁建设,2005(2):1-4.
[2]张仲光,黄彩萍,徐海鹰.混合梁斜拉桥钢混结合段传力机理研究[J].华中科技大学学报:自然科学版,2010,38(5):117-120.
[3]王军文,倪章军,李建中,等.石板坡长江大桥钢混结合段局部应力分析[J].公路交通科技,2007,24(8):99-102.
[4]刘 荣,余俊林,刘玉擎,等.鄂东长江大桥混合梁结合段受力分析[J].桥梁建设,2013(3):33-35.
[5]张国泉,戴少雄.独塔斜拉桥钢混结合段应力分析[J].结构工程师,2007,23(3):26-30.
[6]国家标准局信息分类编码研究所.JTG D62—2004,公路钢筋混凝土及预应力混凝土桥涵设计规范[S].北京:中国标准出版社,2004.
