无轴承同步磁阻电机定子电流内模解耦控制方法
2013-06-19王钧铭张汉年刘合祥
孙 刚,王钧铭,张汉年,刘合祥
(1.南京信息职业技术学院,江苏南京210023;2.东南大学,江苏南京210096)
0 引 言
无轴承同步磁阻电机是在普通同步磁阻电机转矩绕组上再叠加一套用以产生支承转子恒定悬浮的悬浮绕组[1],电机的电磁转矩和悬浮力取决于两套绕组中的电流大小。相比其他类型的交流电机,无轴承同步磁阻电机具有突出的高品质特点:控制简单、转矩脉动低、转速高、免润滑等。无轴承同步磁阻电机的转矩控制部分等同于普通同步磁阻电机,而该电机转矩和转速控制一般采用矢量控制技术[2],其基本思路是将静止坐标下的三相转矩绕组电流通过坐标变换为两相电流:励磁分量电流id和转矩分量电流iq,但id和iq存在交叉耦合,这种耦合关系随着转速增大而增强,无轴承同步磁阻电机一般运行于高速状态,这种耦合关系在高速时会对电机转矩和转速控制产生严重干扰。同时悬浮绕组电流产生的径向悬浮力的大小与电机转矩绕组定子电流也有重要关联[2],在旋转坐标系下,电机转矩绕组电流分量的交叉耦合会进一步增大了悬浮力分量之间的耦合关系,影响电机的悬浮控制性能。
内模控制已成功应用于其他交流电机的电流解耦控制[3-4],本文将内模控制理论应用于无轴承同步磁组电机电流解耦控制,仿真结果证实了该控制方案的有效性。
1 无轴承同步磁阻电机内模解耦控制
1.1 电机转矩控制数学模型
在同步旋转d-q坐标系下,无轴承同步磁阻电机转矩绕组的电压方程[5-6]:
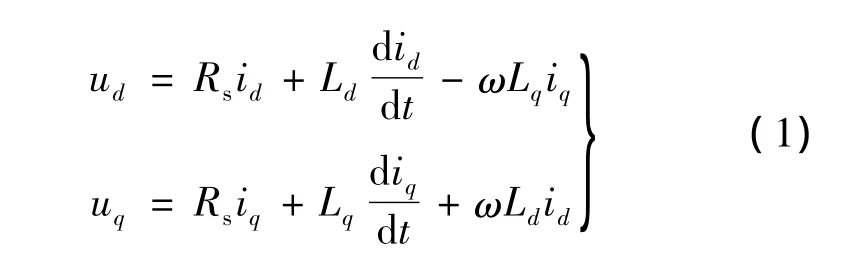
式中:ud、uq为定子电压,Rs为定子电阻,id、iq为定子电流,Ld、Lq为d、q轴电感,ω为转子角速度。
在d、q坐标系下,无轴承同步磁阻电机转矩方程:
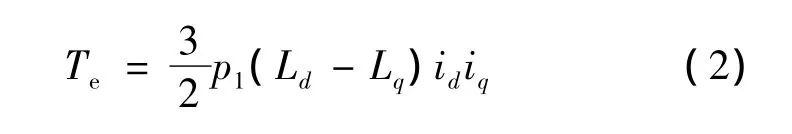
式中:Te为电磁转矩,p1为转矩绕组极对数。
由式(1)、式(2)可见,转矩绕组定子电流两分量之间存在交叉耦合,并相应产生交叉耦合电动势。被控电机转矩和转速控制采用矢量控制技术,当固定id时,电磁转矩受控于iq,但并不能消除d、q轴电流耦合关系,高速时耦合影响更为明显,需对电流进行解耦。
1.2 转矩绕组定子电流内模解耦控制
内模控制的基本原理是把外部输入信号的动态模型引入控制器来构成反馈控制系统,进而设计解耦控制器[7-8]。内模控制及其等效结构图如图1所示,图中R(s)为参考输入,Y(s)为输出,M(s)为内模控制器,D(s)为被控对象,D^(s)为被控对象的估计模型,K(s)为等效的反馈控制器。
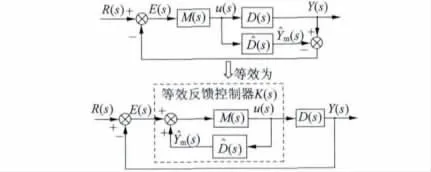
图1 内模控制等效为反馈控制框图
根据内模控制原理,对式(1)进行拉普拉斯变换,可得:
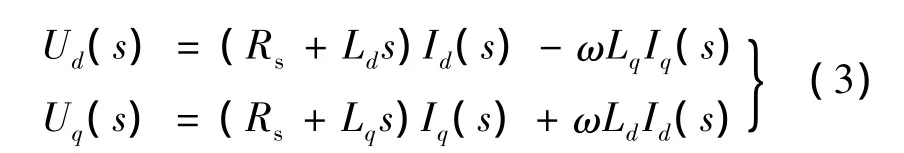
将上式变换可得:
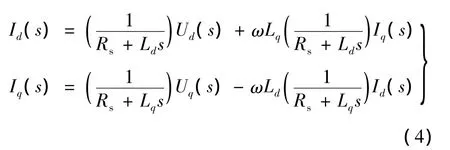
假定U(s)和I(s)分别对应无轴承同步磁阻电机转矩绕组定子电压和电流,令,则有下式成立:
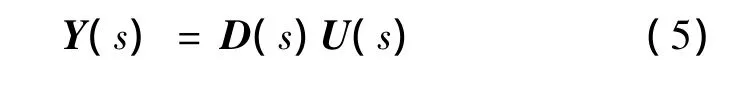
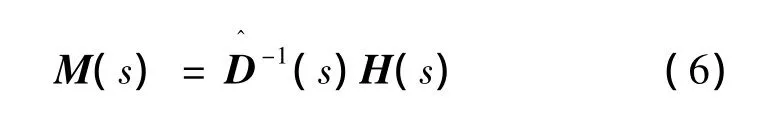
无轴承同步磁阻电机转矩绕组电流传递函数近似为一阶系统,式(6)中低通滤波器H(s)可选为:

式中:k为调节参数,k越大则闭环输出响应越快;I为单位矩阵。
依据式(6)、式(7),构造内模控制器M(s)的表达式:
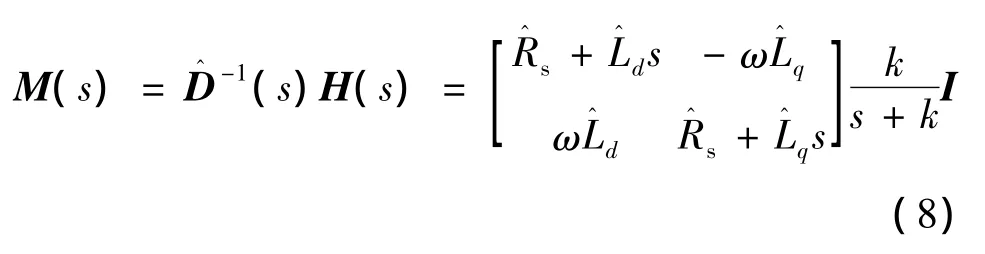
依据图1,将上述内模控制器等效为反馈控制器模型:
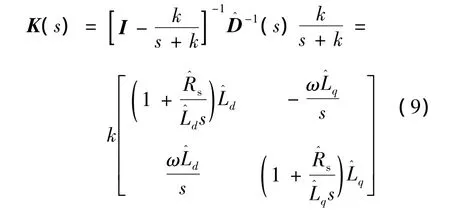
由上式可见,内模控制器增加了反对角线积分项,从而形成解耦网络,将之串接于电机转矩绕组电流耦合模型之前,可消除电流之间的交叉耦合,电流内模解耦框图如图2所示。
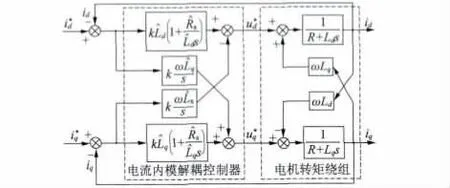
图2 电流内模解耦控制器结构
2 无轴承同步磁阻电机悬浮控制
无轴承同步磁阻电机悬浮系统控制方法是首先建立悬浮力模型,再根据转子位移给定值和检测值之间偏差通过PID调节器生成悬浮力参考值,最终产生悬浮绕组电流信号,实现转子悬浮运行。
在两相静止α、β坐标系下,转子所受悬浮力Fα、Fβ与悬浮绕组电流 iα2、iβ2的关系[9]:
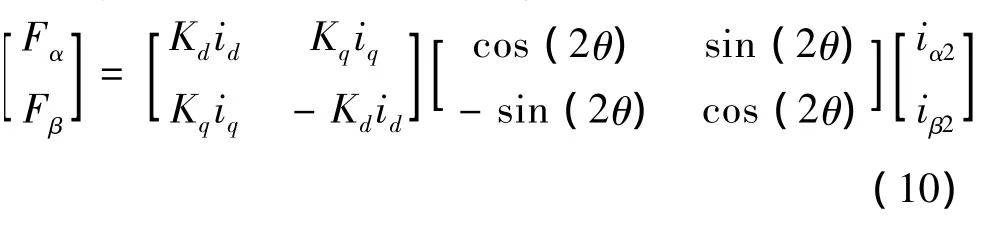
式中:Kd、Kq分别为悬浮绕组d、q轴悬浮力/电流常数[9]。
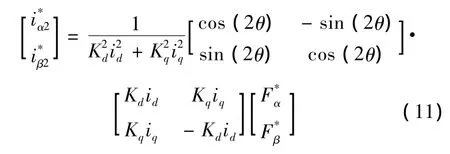
忽略次要因素,理想状态下转子悬浮力与径向位移α、β之间数学方程:
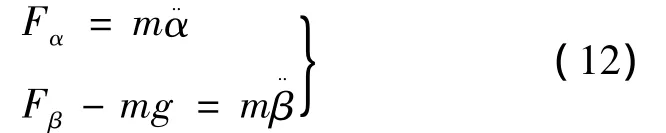
图3给出了包含电流内模解耦控制器、转矩控制和悬浮控制的完整控制系统框图。

图3 无轴承同步磁阻电机内模解耦控制框图
3 仿真结果及分析
在MATLAB环境下进行被控电机内模解耦控制系统的建模和仿真研究,电机仿真参数:Ld=0.05 H,Lq=0.01 H,p1=2,Rs=0.35 Ω;悬浮绕组极对数 p2=1,Lx=Ly=0.04 H,电阻 Rs2=0.3 Ω;转子质量 m=2.5 kg,转子转动惯量 J=0.005 kg·m2,定转子气隙为0.5 mm;电机转子为凸极结构,转子极弧角度为 60°,经估算:Kd=63 N/A,Kq=32 N/A;=0.9Ld、=0.9Lq和=0.8Rs。
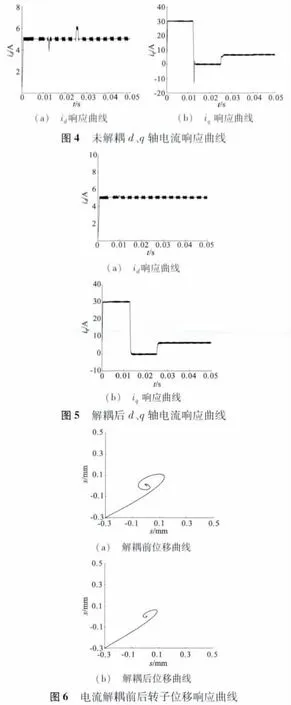
电机转矩绕组励磁电流设定为id=5 A,电机空载起动、在0.025 s时突加5 N·m转矩,同时转速设定为从0上升到1 500 r/min。图4(a)、图4(b)分别是未进行动态解耦的 d、q轴电流响应曲线,可以看出,未进行解耦的两个电流量存在相互影响。
图5(a)、图5(b)分别为采用内模解耦后的d、q轴电流响应曲线,可以看出,解耦后的两个电流动态响应性能良好,相互耦合关系已被解除。
图6(a)、图6(b)分别为内模解耦前后电机转子位移响应曲线,转子初始位置设定为x=y=-0.3 mm,可以看出,电流解耦后悬浮系统控制性能更佳,转子能更好更快地稳定悬浮于x=y=0中心位置。
4 结 语
无轴承同步磁阻电机转矩子系统采用矢量控制时不能对定子电流d-q轴分量进行动态解耦,转矩绕组定子电流分量之间的交叉耦合降低了电机系统的转速和悬浮力控制特性。本文采用了内模控制方法对转矩绕组定子电流进行解耦控制,给出了内模解耦控制器的设计过程,仿真结果表明内模解耦控
制下电机转子具有良好的悬浮运行特性,同时转矩绕组电流分量实现了完全解耦,转速和转矩动态抗干扰能力增强。
[1]Oshima M,Miyazawa S,Deido T,et al.Characteristics of a permanent magnet type bearingless motor[J].IEEE Transactions on Industry Applications,1996,32(2):363 -370.
[2]Hertel L,Hofmann W.Magnetic couplings in a bearingless reluctance machine[C]//International Conference on Electrical Machines.2000:1776 -1780.
[3]范娟娟,骆光照,闫要岗,等.基于内模解耦的IPMSM矢量控制仿真研究[J].计算机仿真,2010,27(10):347 -350.
[4]周渊深,姜建国.异步电动机的动态解耦控制[J].中小型电机,2001,28(2):22 -26.
[5]周立求.ALA转子同步磁阻电机直接转矩控制系统研究[D].武汉:华中科技大学,2005.
[6]Bose B K.现代电力电子学与交流传动[M].北京:机械工业出版社,2006.
[7]杨明,付博,李钊,等.永磁同步电动机矢量控制电压解耦控制研究[J].电气传动,2010,40(5):24 -28.
[8]杨亮亮,周云飞,赵江涛.基于内模电流解耦的PMSM矢量控制研究[J].电气传动,2008,38(9):22 -26.
[9]张汉年,张涛.无轴承同步磁阻电机解耦集成控制策略[J].电气传动,2009,39(9):56-59.