基于正余弦编码器的位置细分技术综述

刘海龙，肖海峰，贺昱曜

(西北工业大学，陕西西安710072)

0 引 言

在高精度、高动态性能要求的伺服系统中，必须实时和精确地测量转子的位置和转速。正余弦编码器正是将旋转轴的机械几何位移转换为数字量的传感器，为转子的位置和转速测量提供了技术解决方案。

正余弦编码器出现于上世纪60年代，在机器人、军工火控等系统中获得了广泛的应用［1－3］。随着伺服系统控制性能要求的不断提高，对转轴位置的定位精度要求也越来越高［4－5］，然而单纯的提高编码器的光栅数，既有成本的限制，又有工艺技术等方面的制约，无法满足高精度及实时性的要求，因此对编码器输出信号进行再细分及滤波等处理方法，一直是重要的研究方向［4－5］。

本文系统地研究了正余弦编码器在电机伺服系统中的应用技术，分析比较了在不同的历史阶段、不同微处理器下的各种典型应用技术方案，总结了各个应用技术方案在不同的工程领域的应用情况，并针对现有方案的研究现状和不足，探讨了在超低速运转时的发展趋势和研究方向。

1 基于单片机的单列脉冲计数技术

正余弦编码器正常工作时，分别输出2N个两路相位相差90°的正弦信号，如图1所示。

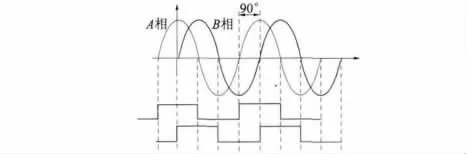
图1 编码器波形

在上世纪80年代及以前，控制系统使用的主控芯片为单片机，使用单片机进行模拟信号处理时效率低、运算复杂，无法满足工程需要。因此采用单片机的系统需要解决以下问题［4－7］:

首先，正弦模拟信号需先转化为脉冲信号，才能输入单片机进行处理。

其次，单片机不能直接识别脉冲到来的先后次序，无法判别转轴的转动方向。

再次，实际应用环境中，由于存在各种各样的干扰因素，码盘必然存在抖动，当码盘在跳变沿处出现往复抖动时，必然会重复计数，导致位置测量失败。

为解决以上问题，众多学者进行了大量的研究。

文献［6］(1994年)设计了一种基于74LS123的鉴向电路，使用两路触发器对称设计，分别将A相和B相脉冲变窄后与另一相信号逻辑“与”操作，就使得单方向旋转时，只有一路脉冲进行计数。此法通过增加专用的计数芯片，完成了模拟信号到脉冲信号的转换及计数功能，降低了MCU的负担;通过同时对两路脉冲分别计数的方式，实现了对运转方向的识别;另外，采用对两路脉冲个数的加减处理，取得了抗抖动的效果。但是，此方案中脉冲变窄后的宽度是由硬件电路决定的，一旦设计完成难以更改，限制了码盘的转速，因此不适合变速旋转场合。尽管如此，该方法在六自由度并联机器人各臂伸长位置测量系统中获得了成功应用。

文献［7］(1995)简化了文献［4］的复杂电路，提出了应用D触发器计数并消除抖动的方案。其消除抖动的依据是脉冲序列的相位关系，即某一相脉冲的上升沿和下降沿必然对应另一相的不同电平状态，若该相两个连续的跳变沿对应相同的电平，则存在干扰。该方法仍然是通过记录一路脉冲个数来进行位置计数，精度低。

2 基于单片机的双列脉冲计数技术

既然用触发器或者延时电路可以计数并进行鉴向，那么通过增加触发器路数，就可以分别处理A相和B相信号，从而同时获得各相脉冲的跳变沿信息，进一步细分精度和消除干扰。使用单片机的系统都是沿着这个思路进行研究的，文献［8－12］就分别提出了使用多路触发器和延时电路将细分精度提高了2倍～4倍，并取得了一定的消除抖动干扰的效果。如文献［9］(1996年)提出的基于D触发器的双列脉冲计数方式，与文献［7］相比，显著的特点就是增加一路D触发器形成对称的网络，从而分别处理正反转时的脉冲信号，细分精度提高了四倍。

另外，文献［8］提出了通用I/O法，利用单片机的通用I/O口直接通过读取编码器脉冲的状态，判断转动方向，同时计量转动角度，如图2所示。

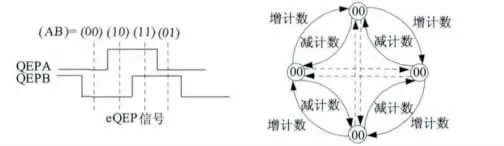
图2 通用I/O口鉴向及计数法

从理论上说，这种方法同时计量了脉冲的上升沿和下降沿，达到4倍的细分效果。另外，抖动时，状态将沿着无效路径变换，通过不进行计数变换从而通过软件方法消除抖动。但这种方法在单片机上使用时存在以下一些问题:首先:该方法需要CPU读取管脚状态，占用了其大量资源，使其效率降低;其次，I/O口的每一个状态都需要及时读取并记录，若下一个跳变沿到来之时，上一个状态尚未读取，将被丢弃，导致时序错误，直接引起系统错误。所以，单片机的读取频率决定了码盘转速，当码盘转速变动时，脉冲序列频率变化与单片机读取间隔不一致，将导致系统无法正常工作，不适用变速控制场合。

3 基于DSP的双列脉冲计数技术

随着微处理器技术的迅速发展，编码器的信号处理技术也得到了不断提高。针对单片机通用I/O口法存在的严重问题［13］，TI等公司的电机控制专用微处理器2812和28335等芯片，集成了两个事件处理器模块(EPWM模块)［17］，该模块包含了正交解码电路，这一电路不依赖CPU而独立运行，正是利用图2的原理，到达了4倍细分的目的。同时，文献［13］还提出通过设置采样频率进行抗干扰滤波的方法。这种计数和滤波方法都不占用CPU资源，极大地提高了控制系统的实时性和效率，已经达到了原始脉冲计数法位置精度细分的极限值。

4 基于DSP的高精度细分技术

随着伺服系统控制精度和性能要求的不断提高以及空间矢量、直接转矩控制等技术的广泛应用，对转子位置测量的精度也有了越来越高的要求。单纯的脉冲计数法无法满足要求。因此，脉冲计数(大角度)加正余弦信号细分角度(小角度)的方式来获得高精度位置信息成为了应用技术研究的重要方案。

因此，自上个世纪90年代以来，特别是最近十年，通过对正交正弦信号进行处理获得相位信息的计算方法吸引了众多研究人员的兴趣。同时，抗抖动算法逐步转化为角度细分算法的研究，因为精度越高，越能识别出真实存在的抖动。当然，由于转轴的机械抖动客观存在，正余弦信号波形本身就会存在畸变，因此需要首先保证正弦信号的质量，才能进一步从中得到精确的位置信息。文献［14］等提出了自适应滤波算法，将正弦信号中的高次波滤除掉，只保留基波，保证了正弦信号的质量，为信号的二次细分技术提供了保障。

文献［15－16］等研究了使用硬件电路比较器法进行角度细分。其思想是:利用比较器设计一个参考电压Up，使正弦信号经过电压比较器，当U≥Up时，电压比较器输出1，当U＜Up时，电压比较器输0。每经过一个Up，比较器便输出一个计数脉冲。选择p个不同的参考电压，比较器便输出p个不同的计数脉冲，相当于将编码输出的脉冲频率提高了p倍，从而精度也提高了p倍。该方法运行速度快、频带范围广，但是硬件电路复杂、成本高、细分精度有限，当细分至12倍频时已经非常复杂，且易引入噪声，抗干扰能力差。

为了得到更高的精度细分角度，在1998年文献［17－18］就分别提出了根据正余弦信号采样值求取反正切值的直接求取法。其思想是对两路正弦信号采样，对比值作反正切计算，直接得到相位值。这种方法可以计算出电机转子的任意位置，精度可以达到微处理器的最高精度，在许多控制精度高的场合获得了应用。

然而求取反正切值需要浮点运算，算法周期长，文献［19］(1999年)提出的闭环跟踪法，避免了反三角函数的计算，对正余弦信号的采样值设置闭环观测器进行相位的识别。在试验中证实了相对于单列脉冲计数法，闭环跟踪法最高达到了2 048倍的细分精度。该方法虽然目前存在运算复杂、迭代步骤不易估计的问题，但也为进一步探索利用其他闭环观测器来获得正弦信号的相位技术提供了一个新的思路。

为了得到更简单的计算方法，文献［20］于2007年提出使用查表法进行角度细分。该方法在微处理器的存储器里预先制定一个表格，根据A/D采样获得的正余弦值来查询表格，从而得到相应的相位值。该方法的精度由A/D采样通道的位数控制，当采用m通道采样器时，相对于单脉冲序列计数法，其细分倍数最高可达2m－2倍。尽管该方法的细分精度不及反正切直接求取法，但表格制作灵活，精度可根据工程需要进行适当调整，相比于硬件方法和反正切求取法有更好的工程实用性。

文献［21］于2011年提出了信号注入法。其原理是根据系统临界稳定原理生成与正弦编码信号等幅值的高频正弦载波，同时采用定时器生成一个与载波相位对应的锯齿波，将高频载波与正弦信号比较，当两者相等时保存锯齿波幅度即可获得正弦信号的相位。该方法易于实现，运行速度快，实时性高，在7 kW无齿轮电梯用永磁同步电机控制系统中获得了良好应用性能。但是该方法需要占用大量DSP的片内资源，精度受反混叠条件等制约，无疑增加了系统成本，应用场合受到限制。

为了得到精度既满足工程需求、计算速度又快的细分角度，文献［22－25］提出了近似线性化方法，研究了函数 Vθ=|sin θ|－|cos θ| 在 θ∈(0，)的范围内近似为线性的特性，根据A/D采样值，将采样结果直接带入线性化公式，根据求解结果进行动态或者查表补偿，得到最终相位值θ。与前述文献提到的方法相比，适当降低了精度，但极大地简化了计算方法，提高了效率，在精度和实时性方面提供了一个平衡点。如本文作者在文献［25］中提到的方法，最高精度可以到达0.12°，而运算速度极大的提高，在某舰载火炮控制系统中获得了成功应用。

5 正余弦编码器发展趋势与研究方向

应该指出，在码盘高速运转时，仅靠脉冲计数计算转子位置误差小，速度快，通常可以满足控制系统性能要求。然而，在一些特殊应用场合，如航天电机控制、太阳能电池板的姿态控制等系统中，电机不仅变速运行，而且运转速度极低，此时位置信息的精度和算法的速度就显得极为重要。然而，目前计算方法中，在极低速时还存在以下问题:细分精度不够;抗抖动方法研究不足;速度计算不合适。因此为了同时提高运算速度，又可以满足工程实际需要的精度，还有以下内容需要进一步研究:

(1)高精度角度细分算法

在运用矢量控制技术、直接转矩控制技术等电机控制系统中，为了提高伺服系统的实时性和稳定性，逆变器的工作频率往往设置为数千赫兹以上，因此进一步简化运算公式、降低运算复杂度，对满足超低速运行时的精度和实时性要求将显得十分重要。

(2)电机极低速运转时的抗抖动研究

在矢量控制技术中，电机转轴的实际转动方向对于调用合适的矢量至关重要。研究中发现，DSP的QEP部分的QDIR位只能用来指示在跳变沿时刻的计数增减方向，当电机运行速度极低时，相邻数次矢量调用都在两个跳变沿之间，无论正转还是反转，此位信息不再变化，因此此时把这个信息位用来作为电机运转方向是不可靠的，有必要进一步展开研究适当的算法，正确识别出电机实际的微小位移，与指令进行适当地逻辑运算，从而确定正确的转动方向，保证下一个矢量调用正确。

(3)电机极低速运转时，速度计算滤波的研究

电机运转时，机械抖动是客观存在的，在极低速时，抖动幅度造成的角位移微分常常会明显高于当前运转速度，造成CPU误判从而输出错误，使电机转速振荡。尽管众多文献分别提出了改进MT法、瞬时速度预估法、变 MT法以及状态观测器法等［26－28］。但是这些方法在极低速时存在执行代码复杂，占用CPU时间太长(瞬时速度预估法和状态观测器法)等问题。

因此，采取何种滤波技术，正确计算电机转子实际的转速，也需要进一步研究。

6 结 语

本文分析了在不同的历史阶段、不同微处理器下的各种典型应用技术方案，指出了各个方案的处理方法、细分精度以及优缺点等，对实际工程中根据系统的精度和实时性要求，选取适当方案具有重要的指导作用。同时，又重点指出了各技术方案进一步研究的方向和建议，根据作者近期的研究成果，提出实际系统工程中在精度和运算速度之间寻找相应的平衡点的思想，提出一些简洁有效的新方案，希望能为相关研究人员提供新的思路。

［1］于春波.关于光学编码器精度和可靠性问题［J］.火控技术，1976(04):67－77.

［2］Beckmann U，Bardenheuer R.High resolution position and velocity measurement with incremental encoders［C］//Proc.SPIE － Int.Soc.Opt.Eng.，1984，444:127 －131.

［3］一机部自动化所.双盘式光电编码器－工业机器人的一种高精度定位检测装置［J］.机械工业自动化，1979(02):39－45.

［4］Lajoie P.Sine wave output improves incremental encoder signal transmission［J］.Control Engineering，1977，24(01):34 －34.

［5］Wrenn RF.A microprocessor－ controlled optical incremental angle encoder system for the picker FACS － I diffract meter［J］.Journal of Applied Crystallography，1979(12):425 －425.

［6］方一鸣.增量式脉冲编码器在绝对位置测量中的应用［J］.自动化仪表，1994，15(08):21 －23.

［7］朱灿焰.抗光电编码器抖动技术［J］.华东交通大学学报，1995，12(04):46 －51.

［8］任作新.提高对增量编码器读数的准确性［J］.自动化仪表，1995，16(12):27 －29.

［9］张锦春，黄树槐.增量式光电编码器在自动测试系统中的应用［J］.自动化仪表，1996，17(02):23 －24.

［10］Ogasawara S.An approach to real－ time position － estimation zero and low speed for a PM Motor Based on saliency［J］.IEEE Trans.Indus.Appli.，1998，34(1):163 －168.

［11］张九才.增量式编码器抗抖性研究［J］.自动化仪表，2005，26(10):38－39.

［12］Chen Minjie，Tian Guozhang.The counter and anti－ jamming circuit for rotary encoder［J］.Application of Electronic Technique，2001(11):70－75.

［13］高伟.增量式光电编码器在交流伺服系统中的应用［J］.电气自动化，2011，33(6):36 －38.

［14］母一宁.应用于增量式光电编码器的相关自适应滤波方法［J］.光子学报，2011，40(10):1452 －1458.

［15］周雪连.正余弦编码器细分技术研究［J］.现代电子技术，2012，35(3):164 －166.

［16］韩念琛.增量式编码器输出信号细分方法研究［J］.太原理工大学学报.2011，42(01):52－54.

［17］Texas Instruments.TMS320F240 DSP － solution for high － resolution position with sin/cos－ encoders［R］.Texas Instruments Insorporated，1998.

［18］Kim Ju － Chan.Ultra precise position estimation of servomotor using analog quadrature encoders［C］//Proc.of IEEE APEC.IEEE，2006:5.

［19］Burke J.Extraction of high resolution position information from sinusoidal encoder［C］//Proc.PCIM － Europe.1999:217 －222.

［20］陈晓荣.增量式编码器的相位编码细分研究［J］.仪器仪表学报，2007，28(01):132 －135.

［21］洪小圆.一种新颖的正弦正交编码器细分方法［J］.电源学报，2011(01):8－11.

［22］Benammar M.A novel rsolver－to－360 degree linearized coverter［J］.IEEE Sensors Jurnal，2004，4(01):96 － 101.

［23］Zhao Ming，Lin Jing，Xu Junhua.The measurement and error analysis of instantaneous angular speed using optical incremental encoder［C］//2011 International conference on optical instruments and technology:Optoelectronic measurement technology and systems.2011:82010Y －82010Y －8.

［24］Alhamadi M A，Benammar M，Ben － Brahim L.Precise method for linearizing sine and cosine signals in resolvers and quadrature encoders applications［C］//Proc.of IEEE IECON.IEEE，2004，2:1935－1940.

［25］刘海龙.麦克劳林级数法求取光电编码器转子位置算法［J］.传感技术学报，2013，26(5):616 －621.

［26］文晓燕.增量式编码器测速的典型问题分析及应对策略［J］.电工技术学报，2012，27(2):185－186.

［27］Liu Zhe.Velocity measurement based on alternate M/T method and incremental optical encoder［J］.Advanced Materials Research，2011，295:2552 －2555.

［28］Ali T，Nayeem S，Faruk M O，et al.Design ＆ implementation of a linear IC based low cost anemometer for wind speed measurement［C］//2012 International conference on Informatics，Electronics and Vision.IEEE，2012:99 －102.