基于WVD－MUISC算法的单矢量水听器DOA 估计＊

张 炜 程锦房 蒋伟涛

（海军工程大学兵器工程系1） 武汉 430033） （91388部队水声对抗技术重点实验室2） 湛江 524022）

0 引 言

波达方向（direction of arrival，DOA）估计是水声信号处理领域中的主要任务.为了突破阵列常规波束形成的空间分辨力限制，出现了基于阵列协方差矩阵特征分解的子空间类MUSIC 算法，实现了向现代超分辨测向技术的飞跃［1－2］；同时为了减小基阵尺寸并能在低信噪比情况下对目标进行高精度方位测量，出现了一类新型水声换能器——矢量水听器，它不仅能获取声压这一声场的标量参数，而且能同时获取质点振速这一声场的矢量参数，为完整地利用声场信息进行后续信号处理提供了充分的可能性［3－4］.单个矢量水听器MUSIC算法能获得阵列信号处理才能得到的高分辨力［5－6］，但是存在着易受外部噪声非平稳性干扰、信号个数受阵元数限制等问题.时频分析是处理非平稳信号的有效手段，它将一维的时间信号变换到二维的时频域，揭示了信号中每一频率分量随时间的变化趋势.将时频分析与MUSIC算法结合起来［7－8］，能同时利用信号的时域与频域的信息提高MUSIC算法DOA 估计的性能.

本文将时频MUSIC算法用于单个矢量水听器，仿真分析了算法的噪声抑制能力、空间分辨能力和多目标分辨能力，为低信噪比下多目标探测阵列的小型化提供技术参考.

1 单矢量水听器MUSIC算法

在各向同性均匀无限大的理想流体介质中，对于单频声波，为简化模型，仅考虑矢量传感器输出同点的声压p（t）和正交的二维振速vx（t），vy（t），ρ0c＝1，则单矢量传感器的数据模型可表示为［9］：

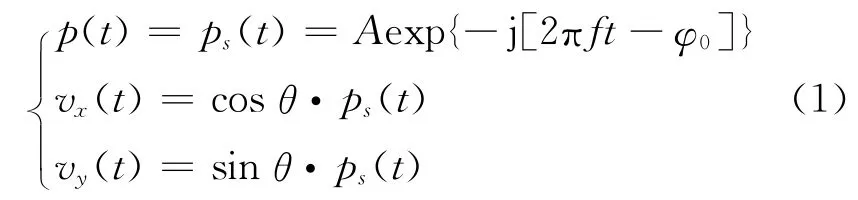
式中：θ∈［0，2π）为入射声波的水平方位角；A 为信号幅值；f 为频率；φ0 为初始相位.上式表明各振速分量只是声压传播方向的余弦加权，且令S（t）＝［p（t），vx（t），vy（t）］T.

考虑到环境噪声场影响的声矢量信号表示为

式中：np（t），nvx（t）和nvy（t）为各向同性噪声干扰.

则采样产生一个3×N 维的矢量水听器阵列矩阵X（t），N 是数据采样点数，在这里，X（t）满足式（2）接收数据模型，此时A（θ）为3×N 维的流型矩阵（由文献［9］），其表达式为

式中：a（θk）＝［1，cosθk，sinθk］T为信号的单矢量水听器阵列流型.单矢量水听器接收数据X（t）的协方差矩阵

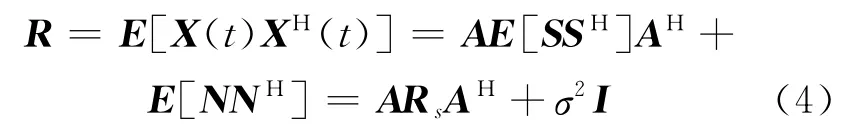
根据子空间分解理论，如果阵列数据的信号分量位于协方差矩阵R 的一个低秩的空间，那么可以通过特征结构类的子空间方法将数据协方差矩阵分解为信号子空间和噪声子空间.

式中：ei为R 的特征值λi对应的特征向量；Λ 为由特征值组成的对角阵；λS为最大的一个特征值；ΛN为（3－1）个较小特征值组成的对角阵，大特征值对应的特征向量构成了信号子空间US，小特征值对应的特征向量构成了噪声子空间UN.

理想条件下数据空间中的信号子空间与噪声子空间是正交的，此时构造入射信号的导向矢量：

育龄期妇女是社会人口的重要组成部分，其也是影响下一代人口质量及人口结构的重要因素。而目前我国育龄期妇女死亡率较高，对社会的稳定发展造成了极大影响，加强育龄期妇女的健康保健工作，如何减少育龄期妇女死亡率是当前社会关注的重点问题[3-4]。本次调查研究显示，育龄期死亡女性中，以45～50岁女性、农民、初中学历、长期在农村居住女性占有率最高，该特征可在一定程度上反映育龄期妇女的死亡特点，可根据上述调查结果，对符合上述特征育龄期妇女实施重点监管，以降低育龄期妇女死亡率。

显然，若导向矢量a（θ）指向信号子空间时，其必与噪声子空间UN正交，则单矢量水听器MUSIC算法的空间谱估计表达式为

2 时频MUSIC算法

2.1 空间时频分布

空间时频分布（spatial time－frequency distribution，STFD）的中心思想是利用wigner－ville分布（wigner－ville distriburtion，WVD）的时频聚集性构造空间时频分布（STFD）矩阵并用该矩阵代替传统的相关矩阵进行DOA 估计，可以有效抑制噪声和干扰，提高算法的稳健性.

WVD－MUSIC算法性能具有显著优势：（1）可以估计数目大于接收阵列通道个数的信号源方位；（2）能对在时频面可以区分而在空间上到达角相近甚至重合的信号进行方位估计；（3）对非平稳信号在构造空间时频分布矩阵时可以确定瞬时频率值，因而构造导向矢量时不必进行频域和空域的二维搜索，减少了运算量［10］.

对于离散的矢量传感器接收信号x（t），其WVD 分布定义为

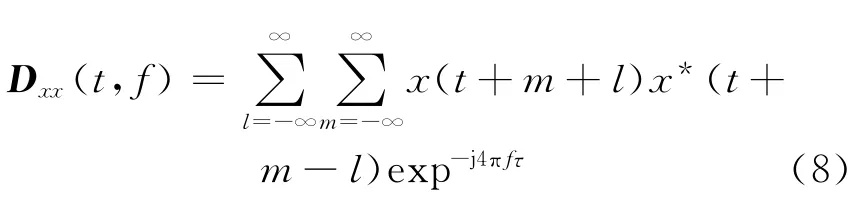
2个离散时间信号x1（t）和x2（t）的互WVD分布定义为

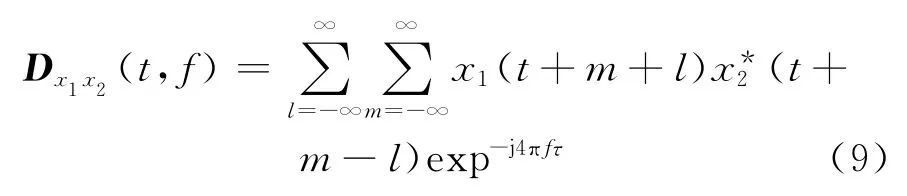
空间时频分布（STFD）定义为

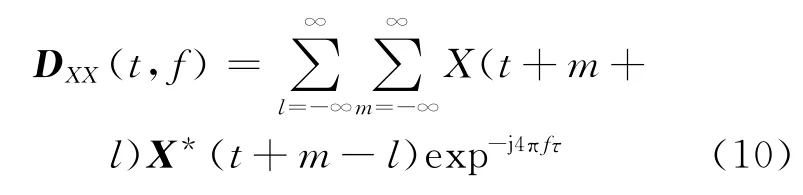
2.2 单矢量水听器时频MUSIC算法

文献［11－12］中证明了空间时频分布矩阵在选定的时频点组成的时频相关矩阵，与数据自相关矩阵特征分解具有相同的信号、噪声空间，表明如MUSIC算法等常规子空间算法的思路和变形可以直接借鉴到空间时频分布中，用接收数据的空间时频矩阵代替空间相关矩阵.

由式（2）和（10），得到单矢量水听器的时频相关矩阵

用CXX代替传统MUSIC算法中的阵列协方差矩阵R，按照单矢量水听器MUSIC算法的步骤，就可以对信号Sk（t）的方位进行估计.通过选择适当的时频点，筛选出相应的有用信号，可以同时抑制其他信号的干扰，因而WVD－MUSIC 算法有很强的信号选择能力.对不同的信号选取适当的时频点分别构造出时频相关矩阵，就能够将各个信号的方位估计出来.为了得到更精确的方位估计结果，可以在不显著增加运算量的情况下，对信号选取一系列的时频点进行估计，将估计结果作平均.

3 仿真分析

对单个二维矢量水听器，分别仿真单目标、双目标和多目标时与原MUSIC 算法对比的结果，验证时频MUSIC 算法的噪声抑制、多目标分辨性能.

3.1 单目标DOA估计

仿真条件：噪声为零均值高斯白噪声，入射信号为θ＝40°，f＝10 Hz的单频信号，采样频率fs＝100Hz，样本点数N＝500，搜索步长为Δθ＝0.01°，计算结果见图1.

从图1中可以看到，WVD－MUSIC 算法的噪声抑制性能和空间分辨力明显优于MUSIC 算法，并且高信噪比时方位估计精度一致，但低信噪比（c）方位估计出现误差时，新方法的方位估计偏差较小.

图1 单目标方位估计仿真结果

3.2 多目标DOA 估计

1）双目标分辨 仿真条件：噪声为零均值高斯白噪声，f1＝20Hz，f2＝10Hz，采样频率fs＝100Hz，样本点数N＝500，且前250个样本数据为f1，后250个样本数据为f2，SNR＝40dB，搜索步长为Δθ＝0.01°，计算结果见图2.

图2 双目标方位估计仿真结果

由图2中可见，随着2目标方位角度从10°减小到2°，MUSIC 算法从能分辨到分辨力减小到不能分辨，并且对比图1可知，由于信号的非平稳性，即使SNR＝40dB，算法的方位估计性能并不比图1a）中SNR＝20dB 时好，而WVD－MUSIC算法首先从时频面上区分信号，因此即使角度很小也能分辨.

2）多目标分辨 仿真条件：噪声为零均值高斯白噪声，入射信号为θ1＝40°，θ2＝30°，θ2＝20°，f1＝20 Hz，f2＝10 Hz，f3＝6 Hz采样频率fs＝100Hz，样本点数N＝500，SNR＝20dB，搜索步长为Δθ＝0.01°，计算结果见图3.

图3 多目标仿真结果

由图3可见，即使信源数等于或者大于单矢量水听器的阵元数，只要信号能从时频面上区分，就能估计出信号方位，突破了原MUSIC 算法信源个数的限制.

4 结束语

本文研究了基于时频MUSIC 的单矢量水听器DOA 估计算法，用基于WVD 时频分析的空间时频矩阵替代MUSIC 算法中的相关矩阵，来进行方位估计，该方法对入射信号选取适当的时频点构造空间相关矩阵，对矩阵分解后通过谱峰搜索得到目标的入射方位.仿真结果表明，新方法有更强的噪声抑制能力和更好的空间分辨力，信号的到达角相近时或信号个数大于阵元个数时，如能从时频面区分信号，就能较准确的估计信号方位角，突破了传统子空间算法阵元数对信号个数的限制.

［1］WANG Xuhu，CHEN Jianfeng.Performance study on several DOA estimation methods based on acoustic vector sensor array［C］∥IEEE International Conference on Signal processing，Communications and Computing，2011（9）：1－4.

［2］姚直象，胡金华，姚东明.基于多重信号分类法的一种声矢量阵方位估计算法［J］.声学学报，2008（4）：305－309.

［3］惠俊英，刘 宏，余华兵，等.声压振速联合信息处理及其物理基础初探［J］.声学学报，2000，25（4）：303－307.

［4］顾晓东，邱志明，袁志勇.基于改进MUSIC 算法的矢量水听器阵列波达方向估计［J］.武汉理工大学学报：交通科学与工程版，2009，33（3）：487－490.

［5］江 南，黄建国，李 姗.单矢量水听器DOA 估计算法研究［J］.仪器仪表学报，2004，25（4）：87－90.

［6］梁国龙，张 锴，付 进.单矢量水听器的高分辨方位估计应用研究［J］.兵工学报，2011，32（8）：986－990.

［7］AMIN M G.Spatial time－frequency distributions for direction finding and blind source separation［C］∥in Proc.SPIE，Vol.3723，1999：62－70.

［8］BELOUCHRANI A，AMIN M G.Time－frequency MUSIC［J］.IEEE Signal Processing Lett，1999（6）：109－111.

［9］孙贵青.矢量水听器检测技术研究［D］.哈尔滨：哈尔滨工程大学，2001.

［10］李秀坤，尹世梅，李婷婷.矢量水听器阵时频MUSIC算法研究［J］.声学技术，2010，29（4）：437－441.

［11］ZHANG Yimin，MA Weifeng，AMIN M G.Timefrequency maximum likelihood methods for direction finding［J］.Journal of the Franklin Institute，2000（337）：483－497.

［12］ZHANG Yimin，MA Weifeng，AMIN M G.Subspace analysis of spatial time－frequency distribution matrices［J］.IEEE Transactions on SP，2001，49（4）：747－759.