交换超立方网的自适应性无死锁路由算法＊

曹入辉，梁家荣，王新阳，豆秋丽

（广西大学计算机与电子信息学院，广西 南宁 530004）

1 引言

互连网络的拓扑结构是计算机科学中的一个重要研究分支，人们已提出了多种互连网络，其中超立方体网络是极具吸引力的网络模型之一。超立方体网络具有正规性、对称性、可靠性、强容错性、可嵌入性、直径短和网络通信能力的可扩展性等优点［1～3］，然而对于n 维的超立方体，在n 值较大时，也就是网络中的节点数很大时，过多的边数使得超立方体网络的实现和扩展很困难，开销和性能提高的对比越来越大。为了保持超立方体网络的优点，同时避开因边数增大给网络的实现和扩展等方面带来的困难，人们转而研究超立方体网络的变种。其中，交换超立方网就是超立方体网络的一个重要变种，它具有非常灵活的结构，可以根据需要很容易地在原有基础上进行扩展；此外，它在和其他超立方体网络的变体比较时有自己独特的优势，即交换超立方网可以作为P2P 环境中的一种逻辑拓扑结构［4］，因此相信交换超立网将会成为未来并行计算机系统中一个重要的应用网络模型。

死锁问题一直是并行计算机系统互连网络路由算法研究中的关键问题，死锁是指系统在某一时刻存在若干信息因彼此等待网络信道资源而永远无法达到终点的情形。在避免死锁的路由算法设计中，可采取以下两种算法：第一种为确定性路由算法，确定性路由算法是指在两个主机之间确定单一的路径；另一种是自适应性的路由算法，它是指在网络节点出错时，算法可通过选择其他路径进行路由，进而提高网络的吞吐量并减少延迟［5］。在无死锁自适应性路由算法的研究中，Dally和Seitz首先提出了虚拟通道的概念，用于建立死锁避免的理论模型。Dinder和Harden把虚拟通道的概念扩展到多个虚拟网络中去，并在此基础上提出了一个无死锁的自适应性路由算法。Chien 和Kim 提出了planar－adaptive算法，该算法是部分自适应性的，并且该算法只需要三条虚拟通道就可避免死锁的发 生。随后，Dong 和Xiang 在planar－adaptive算法的基础上进行改进，提出了一种只需要两条虚拟通道就可以避免死锁的自适应路由算法［6］。

作为未来并行计算机系统中一个重要的应用网络模型，交换超立方网的性能研究具有深远的意义。目前，对于交换超立方网在无死锁路由方面的研究还比较欠缺，开展这方面的研究很有必要。本文首先提出了相似子网的概念，并证明了相似子网和超立方网的同构关系；然后利用将一个物理通道分成两个虚通道进而形成两个不相交的虚拟网络，将不同点之间的路由限定在某一个虚拟网络中的技术，提出了一种自适应性的无死锁路由算法。

2 基本知识和定义

定义1［4］交换超立方网是一个无向图，符号表示为：EH（s，t）＝（V，E），（s≥1，t≥1），其中，V 表示顶点的集合，E 表示边的集合：

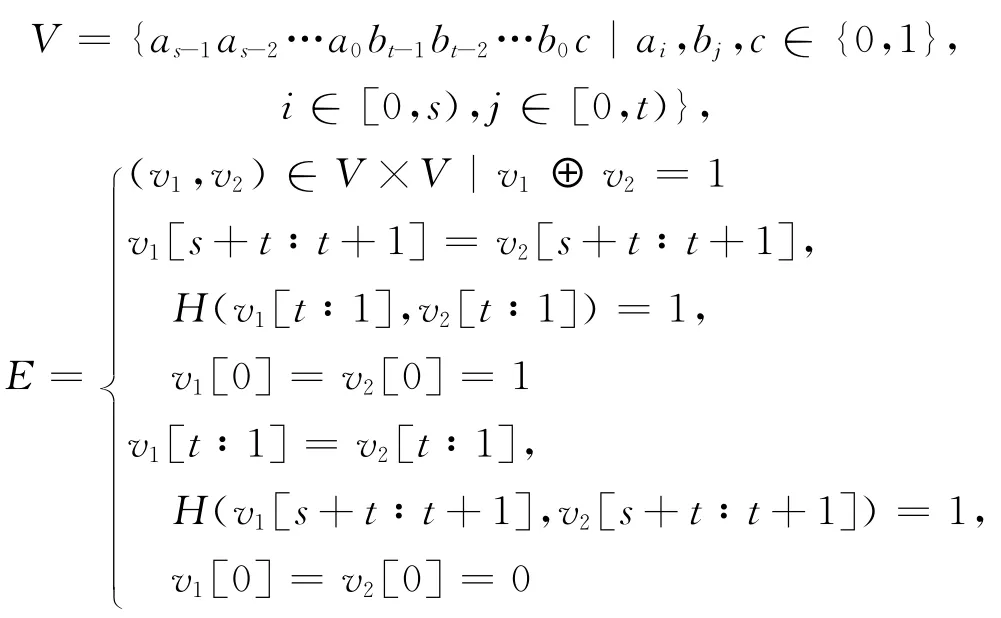
其中，⊕为异或符号；v［x：y］表示字符串v 从x位到y 位的部分字符串；H（x，y）表示点x 到点y的海明距离，并且（x，y）∈V×V。

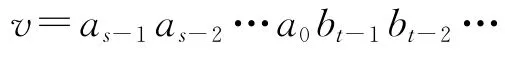
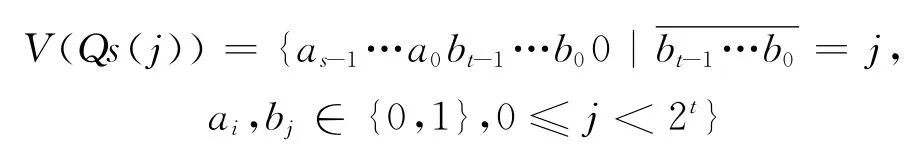
边集E（Qs（j））＝｛（v1，v2）∈E（EH（s，t）），v1，v2∈V（Qs（j））｝。

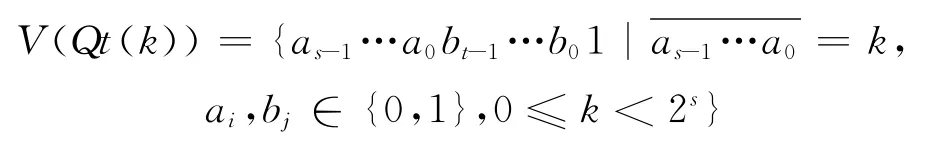
边集为：

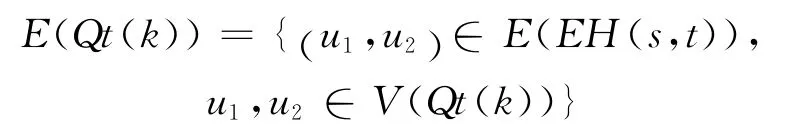
定理1任意Qs（j）与s维的超立方体是同构的，任意Qt（k）与t维的超立方体是同构的。

证明（1）把任意Qs（j）中的节点和s维超立方体网络中的节点进行下列方式的映射：

两个网络的点是一一对应的，并且对应点的边也是一一对应的，则Qs（j）与s维超立方体是同构的。同理可证：任意Qt（k）与t维的超立方体是同构的。

3 无死锁路由算法

对于路由算法的研究是基于文献［7］中等待消息的相关假设。

3.1 超立方体的P－cube路由算法

转弯模型用于超立方体，形成了一种称为P立方路由算法的自适应路由算法［8］。令x＝x1x2…xn和y＝y1y2…yn分别是n 维超立方体Qn中的源节点和目的节点。设集合S 由所有x 和y中不相同的维数构成，即S：＝e＿SCAN（x＋y）。显然S 的大小刚好是x 和y 之间的海明距离。将S 中的元素分成两个不相交的子集S0和S1。如果xi＝0且yi＝1，则ei∈S0；如果xi＝1且yi＝0，则ei∈S1。P－cube路由的基本思想就是将路由选择分成两个阶段。第一阶段，消息先在S0中以任意维序路由，维序的选择取决于选择函数select（）。第二阶段，消息在S1中以任意维序路由，维序的选择也取决于选择函数select（）。如果S0为空，则消息在S1中以任意维序路由，文献［8］中证明了其P－cube算法是无死锁的。下面给出了超立方体的P－cube路由算法。

算法1超立方体最短P－cube算法

3.2 相似子网的最短P－cube算法

算法2s位相似子网的P－cube算法

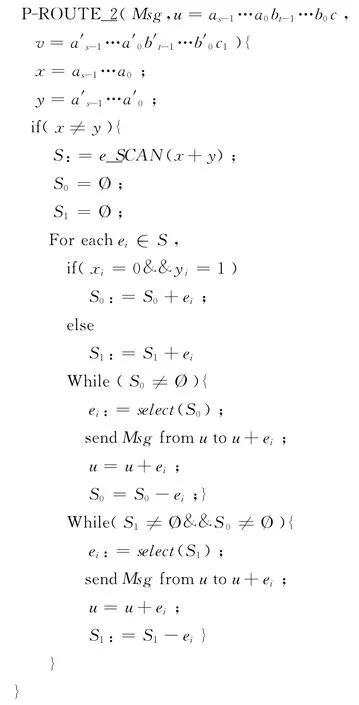
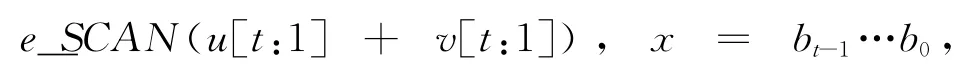
3.3 交换超立方网的路由算法

若所有的节点都只在s位相似子网（或t位相似子网）中路由，只使用算法2（或算法3），算法2和算法3都是避免死锁的，不会出现死锁。若u和v位于不同的相似子网中，s位相似子网和t 位相似子网之间会存在交互，也就是说，在某个s位相似子网（或t位相似子网）发出的消息到达另一个t位相似子网（或s位相似子网），或者经过另一个t位相似子网（或s位相似子网）后到达另一个s位相似子网（或t位相似子网），在这种情况下，就会发生死锁。

为解决这种问题，引入虚拟通道［9，10］（Virtual Channel）构造两个虚拟网络（Virtual Network）来解决路由中出现的死锁问题［11，12］。将每一个物理通道分成两个虚拟通道，分属于两个不同的虚拟网络N1和N2，然后再根据源节点u中的c值判断在哪一个虚拟网络上进行路由。当c＝0时，在N1中路由；当c＝1时，在N2中路由。同时，N1和N2中不存在消息交换，即一旦消息进入了其中一个虚拟网络，它就会在此网络中完成路由，而不会进入到另外一个虚拟网络中。算法如下：

算法4交换超立方网的无死锁路由算法

为了提高路由算法的自适应性，在对s位相似子网和t位相似子网进行路由时采用的是改进后的自适应的P－cube算法。不难看出，算法的时间复杂度为O（s）＋O（t），算法是无死锁的，其无死锁性在3.4节的定理2中得到了证明。

为了验证算法的实用性，在自主开发的交换超立方体网络仿真平台上进行了模拟实验。针对维数为（10，10），（10，15），（15，15），（20，20）的交换超立方体网络，随机设置20对节点进行消息传递，实验结果如表1所示。其中，N 表示交换超立方网的维数，h表示源节点和目的结点不相同维数的个数，path 表示寻得的路径数。从表1中可以看出，算法构建的路径长度path 小于或者等于h＋2，接近于最优路径长度。

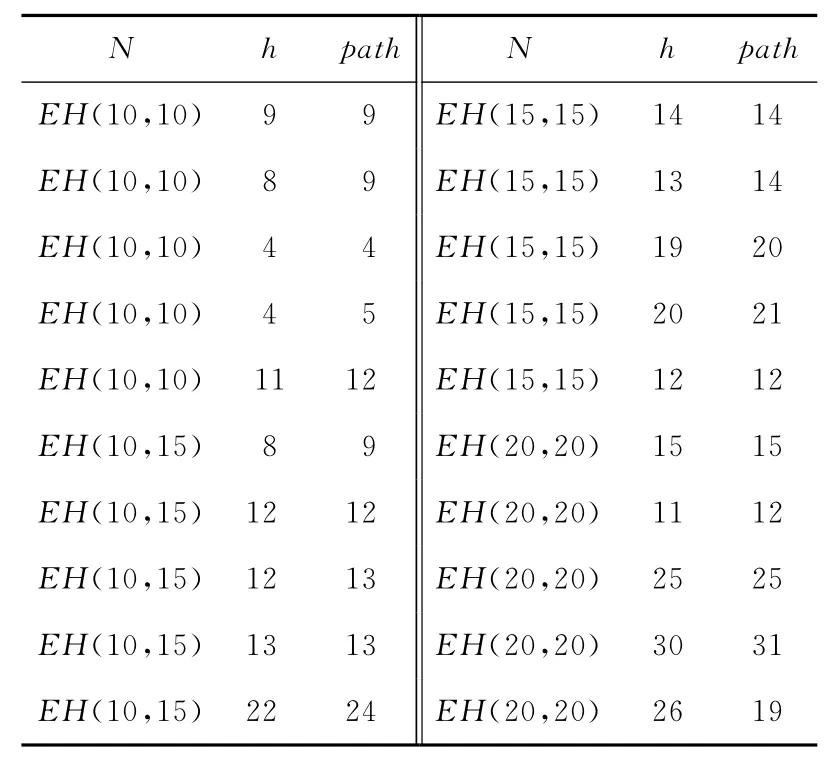
Table 1 Routing result of the algorithm表1 算法寻径结果

3.4 算法4的无死锁性证明

定理2算法4是无死锁的。

证明采用反证法，假设算法4存在死锁。由于路由是在两个互不相交的虚拟网络N1和N2中进行的，故只需分别对N1和N2进行讨论。

假设N1中存在死锁，这就是源节点c＝0时的情况，消息的传送全部在N1中进行。因为在s位相似子网（或t位相似子网）使用的是P－cube算法，故在s位相似子网（或t位相似子网）是不会产生死锁的。那么，当死锁产生时，肯定存在节点u和v 位于不同的相似子网的情况，即s位相似子网和t位相似子网之间存在交互的情况。在分析死锁时，把s位相似子网作为一个网络，把交换超立方网中其他的子网络作为另一个网络来分析，如图1所示。

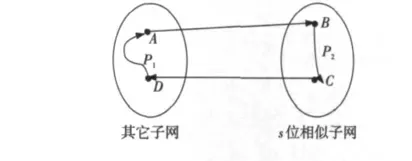
Figure 1 s－dim similar subnet and other subnet图1 s位相似子网与其它子网

设图1 是为一个存在于N1中的死锁配置。A、B、C、D 分别是位于s位相似子网和其他子网的四个节点。AB 和CD 之间有通道相连，节点D 传到A 的消息经过路径P1上的通道，B 到C 经过P2上的通道。作为一个死锁配置，此时应该存在消息占用了通道CD 而申请使用位于P1上的通道。而算法3中在N1路由时，消息在s位相似子网路由完了后再回到其他子网只有一种情况，就是变换C 到达目的节点而不再需要用到其他子网中的任何通道。也就是说，对于从s位相似子网上路由过来的消息，因为D 点已是目的节点，没有消息会在占用CD 通道后再申请位于P1路径上的通道了，这与假设矛盾。因此，算法3 在N1中是不存在死锁的。当c＝1时使用的是N2中的网络。同理可证此时算法中不存在死锁。

综上，由于N1和N2可看成是两个不相交的虚拟网络，彼此间不存在消息交换，故算法4在各自虚拟网络中不存在死锁，整个算法也是无死锁的。

4 结束语

无死锁自适应性路由算法是并行计算机系统互连网络路由算法研究中的关键问题。本文利用虚拟网络技术，即将物理通道分成两条虚拟通道进而形成两个虚拟网络，提出了一种交换超立方网的自适应性的无死锁路由算法，并给予了理论性的证明，这为交换立方体网络安全通信提供了保障。

［1］Sinanoglu O，AlBdaiw B.An inherently stabilizing algorithm for node－to－node routing over all shortest node－disjoint paths in hypercube networks［J］.IEEE Transactions on Computer，2010，56（7）：995－999.

［2］Hsieh Sun－yuan，Chang Nai－wen.Extended fault－tolerant cycle embedding in faulty hypercubes［J］.IEEE Transactions on Reliability，2009，58（4）：702－710.

［3］Liu Ying－ying，Liu Hong－mei.The bipanconnectivity and hamiltonian－connectivity of enhanced hypercube［C］∥Proc of Inte－rnational Conference on Computational Intelligence and Security，2010：454－456.

［4］Loh P K K，Hsu W－J，Pan Yi.The exchanged hypercube［J］.IEEE Transactions on Parallel and Distributed System，2005，9（16）：866－873.

［5］Wang Gao－cai，Wang Guo－jun，Chen Jian－er，et al.Adaptive routing algorithm excel in deterministic routing algorithm［J］.Mini－Micro Systems，2005，26（2）：40－45.（in Chinese）

［6］Xiang Dong.Deadlock－free adaptive routing in meshes with fault－tolerance ability based on channel overlapping［J］.IEEE Transactions on Department and Secure Computer，2011，8（1）：74－87.

［7］Park H，Agrawal D P.A generic design methodology for deadlock－free routing in multicomputer networks［J］.Journal of Parallel and Distributed Computing，2001，61（9）：1225－1248.

［8］Tang Rong－wang，Yang Xiao－fan，Zhu Ce，et al.A deadlock－free routing algorithm for locally twisted cubes［J］.Journal of Chongqing University，2006，29（4）：95－99.（in Chinese）

［9］Zang Ming－xiang，Zhang Xiang－xiang，Jia Wen.Wormhole routing optimization algorithm based on virtual channel switching［C］∥Proc of International Conference on Multimedia Technology，2011：3798－3800.

［10］Dally W J.Virtual－channel flow control［J］.IEEE Transactions on Parallel and Distributed Systems，1992，3（2）：194－205.

［11］Xiang Dong，Wang Qi，Pan Yi.Deadlock－free fully adaptive routing in tori based on a new virtual network partitioning scheme［C］∥Proc of the 37th International Conference on Parallel Processing，2008，10（1109）：612－619.

［12］EI－Darieby M，Rolia J.Hierachical creating of virtual networks［C］∥Proc of IEEE Symposium on Network Operations and Management，2006，10（1109）：220－229.

附中文参考文献：

［5］王高才，王国军，陈建二，等.自适应路由算法优于确定性路由算法［J］.小型微型计算机系统，2005，26（2）：40－45.

［8］唐荣旺，杨小帆，朱策，等.一种基于局部扭曲立方体的无死锁路由算法［J］.重庆大学学报，2006，29（4）：95－99.