短程力分子模拟在Hadoop上的实现及优化＊

焦善飞，何 晨，豆育升，唐 红

（1.重庆邮电大学计算机科学与技术学院，重庆 400065）；2.重庆邮电大学高性能计算与应用研究所，重庆 400065）

1 引言

Hadoop是目前比较流行的开源分布式计算框架，它大大简化了并行程序的设计和开发，使开发者集中精力分析复杂的应用，摆脱并行化过程中的各种困扰。传统的分子动力学模拟研究一般是基于MPI、OpenMP 或Condor网格平台，在可靠性、可扩展性、容错性和动态负载均衡方面均有所欠缺。在传统平台上，个别节点死机时有发生，所有运行的作业都将会受到影响，平台本身缺少自动重新调度子任务的机制，无法在单步内对每个计算节点容错，也不容易在各节点上实现动态负载均衡，以充分利用有限的硬件资源。因此，在Hadoop云计算平台上运行分子模拟程序，具有克服传统平台固有的缺陷、节省各种软硬件投资和缩短模拟时间等意义。

本文在深入研究Hadoop框架及其相关原理的基础上，结合计算化学相关理论，将需要大量计算的短程力有效的分子动力学模拟应用到这种新型平台上来。本文在使用分子动力学模拟常用并行算法，即原子分解法的基础上，提出了三种可行方案并主要实现和测试了其中的“读写HDFS 同步法”，克服了Hadoop实现科学计算类应用的难点——全局通信、同步方式和快速迭代，达到优化模拟、克服传统平台的缺点和提高硬件资源利用率等目的，丰富了Hadoop 在科学计算领域中的应用。

2 云计算和Hadoop

云计算［1］是并行计算、分布式计算、网格计算和虚拟化等技术的综合发展和商业实现，它将大规模的计算任务分解成多个子任务并行运行在大量廉价PC或中低端服务器构成的集群上，具有超大规模、高可靠性、可伸缩性、极其廉价、用户按需使用虚拟化资源池等优点。

Hadoop作为一个分布式系统基础架构，克隆了Google运行系统的主要框架，在底层可以实现对集群的管理和控制，在上层可以快速构建企业级应用。它为应用程序提供了一系列接口，包括分布式计算编程模型MapReduce、分布式文件系统HDFS、分布式数据库Hbase、分布式锁服务Zoo－Keeper等组件。

Hadoop的主从架构如图1 所示，各slave通过网络不断地向master发送heartbeat，获取所要执行的task 或其它操作命令。数据按块（默认64MB）存储在各个DataNode上，NameNode保存元数据并向client提供查询服务。JobTracker接受client提交的作业后将作业划分为多个任务（task），并分发到各个TaskTracker的mapslot／reduceslot（如图1 中mapslot等，表示任务槽）上执行，最后进入reduce 阶段输出执行结果到HDFS。

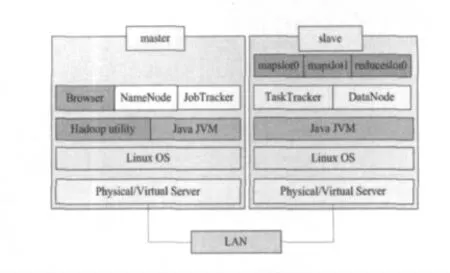
Figure 1 Structure model of Hadoop图1 Hadoop的主从架构模型［2］

Hadoop特别适合高吞吐量、一次写入多次读取类应用，雅虎、淘宝和百度等互联网公司都有多个上千节点规模的Hadoop集群，用于日志分析、数据挖掘和搜索引擎等具体应用，每天运行数万个MapReduce作业，处理PB 级的数据。但是，在科学计算方面的应用还不够广泛，尤其是计算化学中的分子模拟领域，目前在国内外极少有人尝试。

3 分子动力学模拟的概念和原理

分子动力学MD（Molecular Dynamics）模拟是一种在原子级模拟固体、液体和分子性质的常用的计算机模拟方法，广泛应用于物理学、材料科学和生命科学等领域［3］。它主要是通过求解粒子的运动方程，获得其运动轨迹并计算各种宏观物理量。

在模拟过程中需要大量的计算，普通服务器早已不能满足要求，大型机［4］、并行向量机又非常昂贵。使用云计算服务商提供的弹性云计算等方案是比较好的选择，可省去大笔的购置和运维费用，仅需花较少的机时费就可在很短的时间内获得模拟结果，缩短科研周期。因此，将分子动力学模拟这类应用从传统的并行平台迁移到云计算平台上，有着较高的研究意义和实用价值。

下面将分别介绍MD 串行和传统并行算法的基本原理和步骤。

3.1 串行算法

典型的MD 串行算法步骤如图2所示。

Figure 2 Steps of serial MD图2 串行MD 的步骤

模拟体系中每个粒子的运动遵守牛顿运动方程：

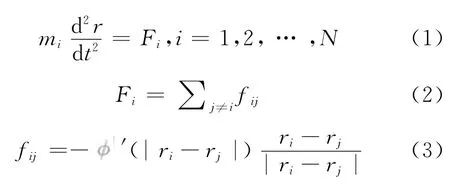
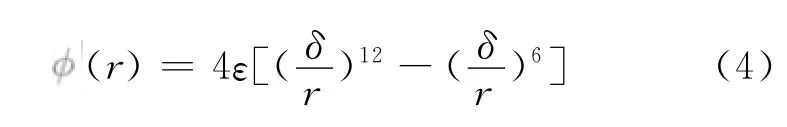
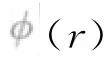
本文使用有限差分法中最常用的verlet－velocity法求解粒子的运动方程：

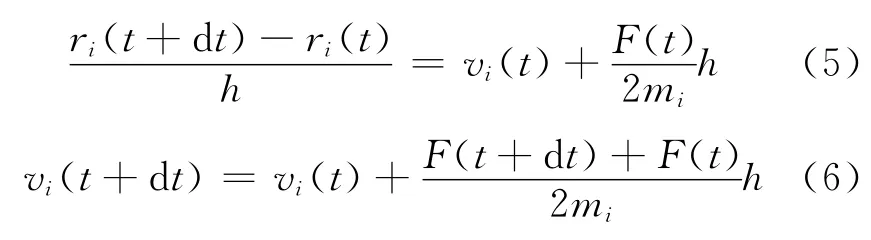
在计算中需要知道上一个时刻的位置、速度和力，首先由方程（5）计算新的位置，然后计算新的力F（t＋dt），再由方程（6）计算新时刻的速度。最后，运用统计物理的方法来计算径向分布函数、总动能、总能量、热传导系数等，达到与实验对照检验，以及指导后续实验研究和预测物质性质等目的［6］。

3.2 并行方案

在模拟过程中，分子间作用力的计算最为耗时，占整体模拟时间的80%左右。有三种并行算法［7］可计算分子间作用力：力分解法、空间分解法和原子分解法。由于Hadoop系统中各计算节点通信时额外开销比较大，不宜频繁通信。而前两种方法都需要频繁的节点间通信，并且并行算法本身也不易负载平衡；原子分解法容易实现，可以实现负载均衡（忙节点少分原子，闲节点多分原子）。因此，本文的程序MRmd采用原子分解法。

传统的MD 并行化是基于MPI、OpenMP［8］或MPI＋OpenMP［9］两级并行的并行机制。MPI是跨节点、消息传递型、进程级并行的编程模型，比较擅长计算密集型应用。OpenMP 是在单机多核平台上、线程级并行的编程模型，由于四路以上服务器价格昂贵，总线和IO 带宽有限，OpenMP 的扩展能力不强。

本文在Hadoop平台上使用MapReduce开源分布式框架来解决MD 这一科学计算问题。采用Hadoop实现MD 相比传统方案有以下优势：

（1）较高的容错性。各节点平等地访问HDFS，每个计算节点（TaskTracker）同时又是数据节点（DataNode）。主节点会把失败的子任务重新调度到另一个节点重新执行，这样就减少浪费宝贵的硬件资源。此外，分布式文件系统的副本策略保证每个数据块都有若干个副本，个别磁盘损坏对整体系统没有影响。而MPI在底层上缺少这种分布式文件系统，一旦中途某个节点宕机，只能将整个作业重新提交；另一方面，在MPI上通常每五个时间步保存一次运行结果，而Hadoop上可以做到保存每一时间步的模拟结果。

（2）较高的资源利用率。每个TaskTracker有多个mapslot或reduceslot，可并行运行多个子任务，最大限度地发挥SMP 和CMP 体系结构的优势，提高资源利用率；另一方面，也不存在MPI上常见的死锁问题。

（3）较强的伸缩性。传统的并行框架伸缩性有限，随着计算规模不断扩大或数据的指数级上升而出现各种瓶颈。而在Hadoop中只需简单地增加节点就能轻松应对新的业务需求。

综上，Hadoop在科学计算类应用和海量数据处理方面都表现出了较好的优势。

4 设计与实现

4.1 难点

常规的Hadoop 应用程序执行流程是：每个maptask（某时刻在mapslot上执行的map 任务）从HDFS取一部分数据作为输入，把每条记录以键值对的形式处理后送到reduce进行规约，再写回HDFS，中间产生的临时数据是先写到本地硬盘再通过网络传输给reducetask（某时刻在reduceslot上执行的reduce任务）。在Hadoop框架中，reduce阶段是实现节点通信的惟一途径。显然，对MD 这种数据相关比较严重并且需要很多次迭代的应用来说，常规执行流程不能满足要求，下一时间步需要上一时间步的全局位置信息。

在Hadoop平台实现MD 的主要困难体现在全局通信、同步方法和快速迭代等方面。当然，在MPI平台上也存在编程困难、通信延迟大、负载不平衡和同步耗时之类的问题。

4.2 解决方案

目前解决方案有：

（1）每个Job计算一个时间步，由Distributed－Cache将上一时间步的全局位置信息分发到各节点的内存中，maptask 负责计算，reducetask 负责汇总全局的新位置信息，然后重新启动一个Job，再进行下一步分发、计算和汇总。这种方法可以用来进行迭代次数不多的模拟，每次迭代要占用大量的作业初始化时间［10］。限于篇幅，本文对该方案的实现和测试不做详细介绍。

（2）读写HDFS同步法。各计算节点平等地访问HDFS，从HDFS 取上一时间步的全局位置信息，把计算好的新位置信息写入到HDFS 供下一时间步的计算节点读取，这是一个很好的实现全局通信的途径。但是，HDFS有自身的缺点——不支持文件的追加，HDFS作为Google GFS的简化版和开源实现，去掉了GFS最复杂的部分，即多个客户端对同一文件的并发追加。程序使用的同步方式为阻塞式通信，直到最慢的节点的计算完成，才能进入下一轮计算。本文的程序MRmd正是采用了这一方案，在设计部分有详细阐述。

（3）使用专门的节点负责同步和分发新的位置信息。此方法又可分为两种：一种是在应用程序上实现，选一个节点（比如taskid＝0所在节点）来收集各计算节点报告的新位置信息，并回复全局位置信息以进行下一时间步的模拟；另一种方法是在Hadoop系统底层实现，各计算节点使用消息传递机制来实现通信。理论上后者能进一步降低全局通信在总时间中的比重，但还未得到实验证明。

4.3 设计

MapReduce采用key－value即键值对的形式序列化每条数据记录［11］，maptask 中有一个用户自定义的map（）函数，该函数接受一个键值对，处理后输出。maptask 处理完split内的键值对后，reducetask便开始复制其输出，以进行shuffle、sort和reduce等工作［12］。

在图3中各模块的具体任务是：

（1）initialize：包括Java JVM 的启动及初始化和为当前 maptask 做的初始化工作，如取maptaskID、分得的原子号列表，申请内存空间保存全局原子的三维坐标、速度和加速度等。

（2）read global：读HDFS中指定的目录下的所有文件，这些文件是由上步计算完成后写入的，提取全局原子ID 及位置信息。

（3）force：对分得的原子号列表中的每一个原子，分别用verlet－velocity 差分和Lennard－Jones作用势计算其新的位置信息。

（4）sync wait：把分得的原子列表中所有原子新位置信息写到 HDFS 中以时间步序号和maptaskID 命名的文件上，进入同步等待阶段，不断检查HDFS的目录下本轮输出文件是否齐全，若不齐全则说明仍有未完成的子任务，循环等待直到所有子任务都完成再进入下一时间步的计算。

（5）reduce phase：map phase完成后输出一个键值对，该键值包括子任务ID、各部分耗时等信息，reduce phase对所有输出汇总，并写到HDFS，以便分析。

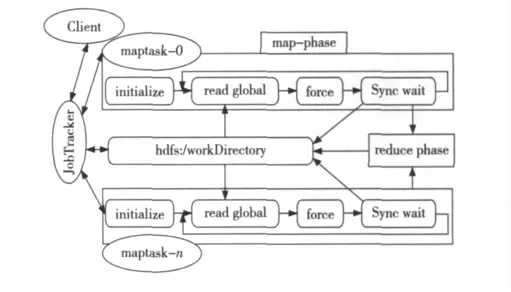
Figure 3 Flow of MRmd图3 MRmd的执行流程图

在模拟结束后，启用另一个Hadoop 程序MRmdEnergy来对所有时间步的位置信息生成统计信息，如每一时间步的温度、动能、势能、总能量、可供jmol软件导入演示动画用的坐标文件和每个子任务的各部分耗时情况。比如maptask0取1～100时间步的所有位置信息，计算其各步的统计信息。为了保证两个reduce phase输出都按时间步有序，设计了特殊的key 并重写了Partitioner－Class。

5 测试与分析

根据Amdahl定律，加速比的定义为：

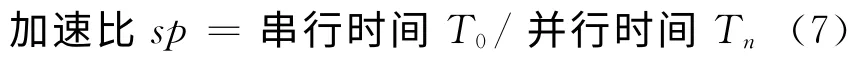
由Amdahl公式知，加速比是有最大限度的，最大值取决于不可并行部分所占的比重。

本文的测试环境为：1个主节点，17个计算节点，配置均为Intel Q6600＠2.4GHz四核CPU，8GB内存，1 500GB 硬盘，百兆网络。每个计算节点配置4 个mapslot，即最多可同时执行4 个maptask。

经典的分子动力学模拟在研究阶段常选用液态氩的分子运动作为研究对象。当氩原子数分别为36 000、60 000和108 000，模拟200步，分别使用maps个子任务对该体系进行测试，测得的加速比（对比MPI＋OpenMP混合并行）如图4所示。从图4中可看出，当原子数为36 000时，Hadoop平台的性能稍逊于传统并行平台，具体原因为上文中所指出的与HDFS通信开销大有关。同步时间、IO 时间和各种附加开销都是不可并行的，即使再增加节点数，加速比也不会有大幅提高。当模拟体系增加到60 000和108 000时，Hadoop表现出了一定优势，在本文实验结果中模拟时间缩短5%。随模拟原子增加，该优势会逐渐凸显，输出文件中模拟体系的总能量随时间变化在十万分位守恒，说明了模拟程序在可接受误差范围内的准确性。

Figure 4 Speedup图4 加速比

当原子数为60 000时，随maps 增加，在所有节点上各部分的平均时间比重如图5所示。

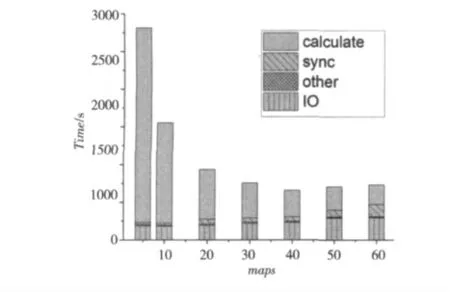
Figure 5 Ratio of cost－time图5 各部分时间比重

（1）其它开销（other）：包括作业初始化1s，分发子任务到所有计算节点、启动JVM、初始化各类参数3s，reduce 阶 段 的shuffle、sort、reduce 占12s，总计16s左右，都是分布式系统框架内必不可少的开销。

（2）平均IO 时间（IO）：读取HDFS得到全局位置信息、写入新位置信息到HDFS 的总时间。由于HDFS是网络上的分布式文件系统，IO 开销＝网络开销＋磁盘开销。

（3）平均同步等待时间（sync）：每一轮检查各子任务是否都同步完成的等待时间。同步越来越耗时是因为每个节点有4个mapslot，可能占了1～4个不等的slot，造成节点负载有轻有重，以及受操作系统的进程调度机制、系统进程不断变化和其他用户进程的影响。

（4）平均计算时间（calculate）：所有子任务有效计算时间的平均值。

总体分析来看，第二种方案本身的通信方式以及集群中百兆网络的低带宽、高延迟，各节点负载不平衡造成同步等待比较耗时，是制约加速比继续提高的重要原因。正因为读写HDFS法实现同步与通信的代价略高，适合用于节点间通信不太频繁、通信量也不大的场合中，所以本程序在大体系模拟时表现更好。

进一步优化程序以实现动态负载平衡，即每一轮都要对比上一轮各子任务的执行时间，如果差值超过一定范围，就把原子重新分配来调整任务粒度，把运算慢的节点上的原子减少，增加给运算快的节点。实验表明，当原子数大于36 000时，负载平衡所引入的额外开销远小于改进前的同步时间。

6 结束语

本文采用MapReduce分布式编程模型结合原子分解法这一并行算法实现并优化了短程力下的分子动力学模拟的并行算法，通过增加适量的IO就可以应对节点失效问题和实现全局通信，并在集群上以模拟不同体系大小的液态氩为例进行了多种测试，取得了较好的加速比、扩展性和容错性。实验证明，Hadoop并行平台在应用于大体系的分子模拟时，不仅在性能上优于传统并行平台，而且弥补了传统平台在负载均衡和容错等方面的不足。但是，Hadoop在科学计算应用上仍然有很多挑战和不足，比如节点间通信不便和实时性不强。为了解决这些问题，下一步将从Hadoop底层通信机制进行改进，探索一种适合此类科学计算的二次开发的并行框架。MD 方面将引入verlet近邻表［13］降低算法复杂度，以加速模拟体系使其尽快达到平衡态。

［1］Weinhardt C，Anandasivam A，Blau B，et al.Cloud computing—a classification，business models，and research directions［J］.Business ＆ Information Systems Engineering，2009，1（1）：391－399.

［2］Liu Peng.Cloud computing［M］.Beijing：Publishing House of Electronics Industry，2010.（in Chinese）

［3］He Mu－jun，Guo Li，Yan Li.Research and analyze of commu－nication performance optimization in large－scale particle simulation system［J］.Computers and Applied Chemistry，2008，25（9）：1－3.（in Chinese）

［4］Zhang Bao－yin，Mo Ze－yao，Cao Xiao－lin.Performance optimization of a molecular dynamics code based on computational caching［J］.Computer Engineering ＆ Science，2009，31（11）：77－83.（in Chinese）

［5］Verlet L.Computer experiments on classical fluids thermodynamical properties of Lennard－Jones molecules［J］.Phys－Rev，1967，159（1）：98－103.

［6］Zhang Qin－yong，Jiang Hong－chuan，Liu Cui－hua.Research of optimization and parallelization for molecular dynamics simulation［J］.Application Research of Computers，2005，22（8）：84－86.（in Chinese）

［7］Wang Bing，Shu Ji－wu，Zheng Wei－min.Hybird decomposition method in parallel molecular dynamics simulation based on SMP cluster architecture［J］.Tsinghua Science and Technology，2005，10（2）：183－188.

［8］Bai Ming－ze，Cheng Li，Dou Yu－sheng，et al.Performance analysis and improvement of parallel molecular dynamics algorithm base on OpenMP［J］.Journal of Computer Applications，2012，32（1）：163－166.（in Chinese）

［9］Li Hong－jian，Bai Ming－ze，Tang Hong，et al.Application of hybrid parallel algorithm for simulating photochemical reaction［J］.Journal of Computer Applications，2010，30（6）：1687－1689.（in Chinese）

［10］Chen He.Molecular dynamics simulation based on hadoop MapReduce［D］.University of Nebraska－Lincoln，2011.

［11］Dean J，Ghemawat S.MapReduce：Simplified data processing on large clusters［C］∥Proc of the 6th Symposium on operating Systems Design and Implentation，2008：1－12.

［12］White T.Hadoop：The definitive guide［M］.California：O’Reilly Media，2009.

［13］Shu Ji－wu，Wang Bing，Chen Min，et al.Optimization techniques for parallel force decomposition algorithm in molecular dynamic simulations［J］.Computer Physics Communications，2003，154（2）：101－103.

附中文参考文献：

［2］刘鹏.云计算［M］.北京：电子工业出版社，2010.

［3］何牧君，郭力，严历.大规模并行粒子模拟系统通信性能优化研究与分析［J］.计算机与应用化学，2008，25（9）：1－3.

［4］张宝印，莫则尧，曹小林.基于计算缓存方法的分子动力学程序性能优化［J］.计算机工程与科学，2009，31（11）：77－83.

［6］张勤勇，蒋洪川，刘翠华.分子动力学模拟的优化与并行研究［J］.计算机应用研究，2005，22（8）：84－86.

［8］白明泽，程丽，豆育升，等.基于OpenMP的分子动力学并行算法的性能分析与优化［J］.计算机应用，2012，32（1）：163－166.

［9］李鸿健，白明泽，唐红，等.混合并行技术在激光化学反应模拟中的应用［J］.计算机应用，2010，30（6）：1687－1689.