Entropy Analyses of Droplet Combustion in Convective Environment with Small Reynolds Number*

ZHANG Xiaobin (张小斌), ZHANG Wei (张伟) and ZHANG Xuejun (张学军)**

Institute of Refrigeration and Cryogenics, Zhejiang University, Hangzhou 310027, China

Entropy Analyses of Droplet Combustion in Convective Environment with Small Reynolds Number*

ZHANG Xiaobin (张小斌), ZHANG Wei (张伟) and ZHANG Xuejun (张学军)**

Institute of Refrigeration and Cryogenics, Zhejiang University, Hangzhou 310027, China

This paper analyzes the entropy generation rate of simple pure droplet combustion in a temperature-elevated air convective environment based on the solutions of flow, and heat and mass transfer between the two phases. The flow-field calculations are carried out by solving the respective conservation equations for each phase, accounting for the droplet deformation with the axisymmetric model. The effects of the temperature, velocity and oxygen fraction of the free stream air on the total entropy generation rate in the process of the droplet combustion are investigated. Special attention is given to analyze the quantitative effects of droplet deformation. The results reveal that the entropy generation rate due to chemical reaction occupies a large fraction of the total entropy generated, as a result of the large areas covered by the flame. Although, the magnitude of the entropy generation rate per volume due to heat transfer and combined mass and heat transfer has a magnitude of one order greater than that due to chemical reaction, they cover a very limited area, leading to a small fraction of the total entropy generated. The entropy generation rate due to mass transfer is negligible. High temperature and high velocity of the free stream are advantageous to increase the exergy efficiency in the range of small Reynolds number (<1) from the viewpoint of the second-law analysis over the droplet lifetime. The effect of droplet deformation on the total entropy generation is the modest.

entropy generation, exergy analysis, droplet combustion, numerical simulation

1 INTRODUCTION

Understanding the physical process of single droplet combustion under various ambient conditions is important for increasing fuel combustion efficiency, a topic that is strongly motivated by the requirement for efficient use of available energy and a clean environment in the operation of power industry and transportation applications. Analysis of entropy generation and exergy loss is an effective tool for evaluating the performance and minimizing the second-law irreversibility in the combustion process of fuel droplets. The conventional energy-based definition of efficiency for a combustion process explains how much thermal energy is obtained from the chemical energy of the utilized fuel, and ascribes the efficiency decrease to external phenomena such as incomplete combustion and heat loss to the surroundings. These analyses fail to identify the deviation from ideality and do not account for the quality of heat as the product of combustion [1]. Several studies have indicated that the combustion process involves interior thermodynamic losses, which significantly limits the conversion of fuel energy into work [2, 3]. These loss mechanisms include the internal mass and heat transfer and the chemical reactions, and can be explained by the exergy-based thermodynamic analysis.

Generally, there are two ways to evaluate the exergy efficiency in a process: exergy analysis approach [3] and minimization of entropy generation approach [4]. The former calculates the exergy flow rate at the boundaries and does not calculate the detailed irreversibility in the process, and therefore does not throw any light on the causes of the irreversibility. A comprehensive documentation of this work can be found in Moran [3]. In contrast, the later approach, based on the principle that a minimization of process entropy generation will lead to the maximum utilization of energy resources, directly evaluates the entropy generation from intrinsic losses. Therefore, the minimization of entropy generation approach can provide more information on the causes of irreversibility and has become a useful tool for studying the exergy efficiency in premixed or non-premixed combustion processes. However, before performing the entropy generation analysis, the basic flow and thermodynamic parameter distributions including temperature, velocity, species concentration and chemical reactions rate have to be known. Thus, the solution of the conservative equations of mass, momentum, species and energy is the first and necessary step for the analysis of subsequent intrinsic entropy generation.

The mass and heat transfer processes associated with single pure droplet combustion in a convective air environment have been analyzed for decades by several researchers [5-7]. According to the developing history, the mathematical strategies used to describe the droplet combusting processes have evolved from one-dimensional [5] to two-dimensional spherically symmetric [6], and now to axisymmetric [8]. The thermophysical properties of the gas mixture are calculated by methods ranging from the “1/3 rule” [9], to those considering temperature and concentration dependence [6, 8]. Although these works provide a picture ofthe quantitative distribution of field variables, no further second-law analysis has been conducted. Even now, publications presenting thermodynamic studies pertaining to an entropy analysis of an evaporating and burning droplet are still few in number. Dash and Som [10, 11] were perhaps the pioneers in ascertaining the entropy generation during the combustion process of a single droplet. In their numerical solutions for the mass and heat transfer processes between the phases, spherical symmetry and quasi-steady conditions were assumed for energy transport associated with the droplets. They found that the irreversibilities in the droplet phase were quite insignificant compared to those in the carrier phase and the most significant contributions were due to the chemical reaction, heat conduction and combined heat and mass convection. The effects of pertinent parameters on the entropy generation rate per surface area of the droplet were specially analyzed and an experiential correlation was derived. Puri [4] analyzed the entropy generation of a droplet burning in a low Reynolds number gaseous stream with the control volume approach, and obtained the optimum transfer number for minimizing entropy generation by comparing the contribution to the entropy generation due to mass loss from the droplet and the drag force. The analysis was based mainly on empirical formula for mass and heat transfer coefficients between the gas and the droplet, and on the assumption that the flame temperature was equal to the average flow temperature. The entropy generation for droplet burning in a quiescent and high temperature gaseous environment was investigated by Hiwase et al. [12] and Lior et al. [13] using spherical symmetry and a one dimensional model. Based on fundamental information of entropy generation in single droplet combustion, the entropy generation analysis for the process of fuel spray evaporation in hot gas surroundings was also made by Som and Dash [14]. Recently, Pope et al. [15] performed an entropy generation analysis for methanol droplets in a quiescent and convective air environment. Som et al. [1] performed a detailed and comprehensive review of the thermodynamic analysis of droplet combustion.

Although significant effort has been made by researchers, there are still various problems that are unresolved regarding the entropy generation for droplet combustion processes, such as the effects of droplet deformation. The present paper addresses these problems by analyzing the entropy generation of a decane droplet combusting in a low Reynolds number and high temperature air-flow medium. Compared to the works by Dash and Som [10, 11], this work (a) eliminates the assumption of a quasi-steady process and spherical symmetry; (b) uses temperature- and species-dependent physical properties for the gas phase in flow field simulations; and (c) provides parametric studies of the effects of temperature, velocity and oxygen fraction in the free stream, and droplet deformation on the entropy generation rate. The flow field simulations of droplet burning in the convective environment have been evaluated in detail elsewhere [16]. Therefore, this paper focuses on the computation of the rate of entropy generation.

2 PROBLEM SPECIFICATION

The configuration for the droplet-air opposing convective flow is illustrated in Fig. 1, which is the same as in a previous publication on mass and heat transfer studies conducted by the present author [16]. The entire computational domain is 20 mm long and 5 mm wide, and is large enough to include the region of influence from the wake, and to ensure that the boundary conditions at the far-stream are truly realized [17]. The air comprising 23% mass fraction oxygen and 77% nitrogen enters the computation domain with a uniform free stream velocity of 0.3 m·s−1, a temperature of 1000 K and a pressure of 1×105Pa. The n-decane droplet was injected into the domain with an initial diameter of 0.1 mm, a temperature of 300 K, and a velocity of 0.05 m·s−1in an opposite direction to the free stream, giving the droplet an initial Reynolds number about 0.26 calculated using air physical properties at the inlet conditions. Once the droplet is introduced, its temperature begins to rise, and consequently, some of its mass begins to vaporize at its surface. The vaporization rate gradually increases as the droplet heats up. Subsequently, combustion is initiated, that being mainly determined for such a low Reynolds number by the diffusion of fuel vapor and oxidizer. Some of generated heat due to combustion will go to the droplet and the rest will heat the ambient gases.

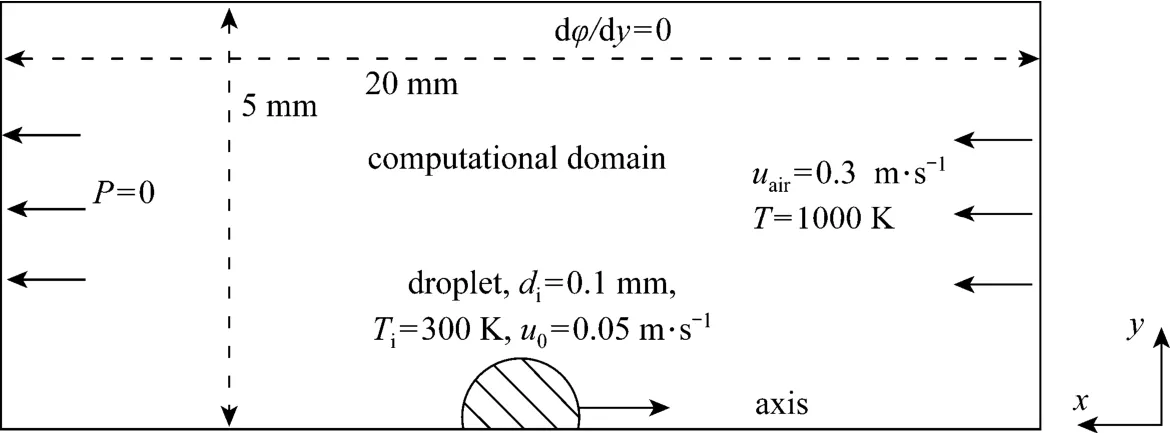
Figure 1 Schematic of droplet vaporization in a convective air flow

In our previous computations using CFD modeling for the mass and heat transfer process [16], the volume of fluid (VOF) mathematical formulation wasused with a 2D axisymmetric model. The simulations successfully captured the transient history of droplet deformation. Other phenomena, such as the temporal flame structure and species concentration distribution were also presented. The resulting velocity, temperature and species concentration distributions have made it possible for the entropy generation analysis of the present work.

3 MA THEMATICAL MODELS

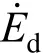
where Δ and σ are the rate of strain and stress tensors, respectively, T is local temperature, µcis chemical potential, s is magnitude of entropy, ω is the chemical reaction rate, and Jmand Jqare respectively the mass and heat flux vectors. The subscript i stands for species. The first term on the right hand side represents the contribution of fluid friction; the second term is the entropy generation rate due to mass transfer, the third due to heat transfer, the fourth due to the coupling between heat and mass transfer, and the fifth due to the chemical reaction. The velocity of flow in the gas phase is very small compared with the local acoustic speed and hence the effect of viscous dissipation, namely the first term of Eq. (2), can be omitted.

The total REG in the whole flow field at any instant is calculated from:

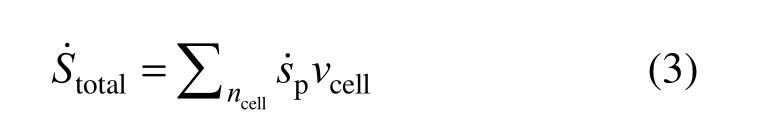
where vcellis the unit cell volume. The total entropy generation over the droplet lifetime is determined by:

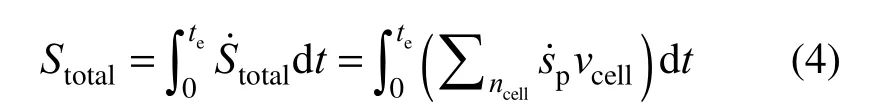
To determine the REG as a function of the temperature, species concentration and chemical reaction rate, each term of Eq. (2) except the first term has to be expanded. The chemical potential of a single species i as an ideal gas reduces to the Gibbs free energy, written as:

where h is enthalpy value. If species i in ideal gas mixture experiences an isothermal transition, Eq. (5) leads to Eq. (6) [3]:

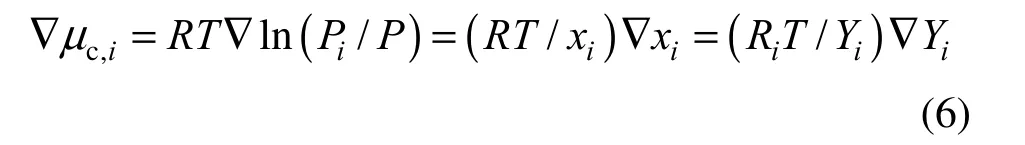
where R is universal gas constant, Riis the gas constant for species i, and Piand P are the partial pressure and total pressure, respectively. The mass and thermal fluxes per unit area Jmand Jqare calculated respectively as:

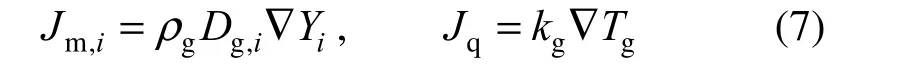
where ρ is density, Diis diffusive coefficient for species i, k is thermal conductivity and subscript g means gas phase. Substituting Eqs. (5)-(7) into Eq. (2), one obtains:

whereiλ′,iλ′ are the stoichiometric coefficients on the reactant side and product side, respectively. The physical quantities in Eq. (8) only comprise the state variables, and all of them can be read directly or indirectly from a previous flow field solution. Therein, the enthalpy of species i is calculated from

and the entropy from

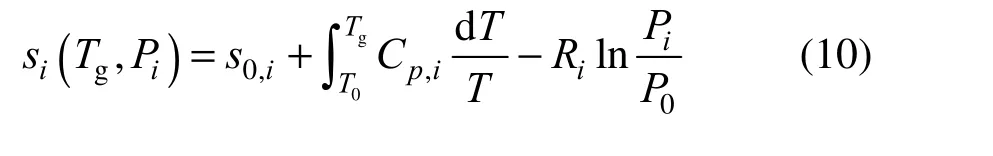
where s0,iand h0,iare the formation entropy and enthalpy of species i, respectively, at reference temperature T0and pressure P0which are set T0=298.15 K and P0=1×105Pa in our case. Cp,iis specific heat of species i, which is calculated as a function of temperature. The chemical reaction rate ω in Eq. (8) for the chemical reaction process

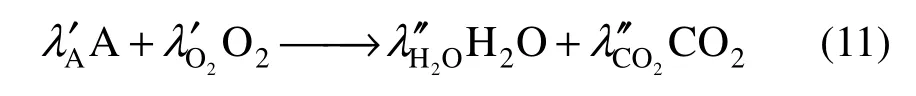
is calculated from

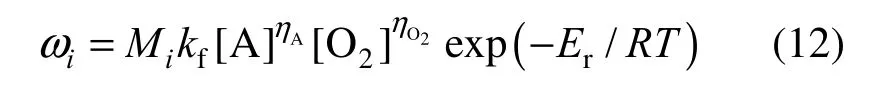
where Miis the molecular mass of species i and kfis the reaction pre-exponential factor. The symbol [ ] stands for the molar concentration of the species, η is a rate exponent and Eris the chemical activation energy. For a decane/air combustion, the following constants are adopted in our simulations: ηA=0.25, ηO2=1.5, kf=2.587×109and Er=1.256×108J·kmol−1[19].

4 RESUL TS AND DISCUSSION

4.1 Effects of free stream

To investigate the effects of the free stream on the total REG of the droplet combustion process, four Cases, from Case (a) to Case (d) listed in Table 1, are modeled. These represent different free stream temperatures, velocities and oxygen mass fractions. The results of the transient histories of the total REG are shown in Fig. 2. For the Cases with the same free stream oxygen mass fraction of 0.23%, all curves exhibit a spike. At the initial time of the process, the total REG is small and gradually increases since the potential gradients, such as temperature and species concentration only exist in very limited regions near the phase interface, and the chemical reaction is insignificant as a result of the low concentration of reactants. As the heat and mass transfer between the phases increases, the droplet heats up, the region of effluence of the droplet extends, and the REG increases. After a certain time, for example, after about 2 ms for Case (a), the increase of REG is obviously accelerated until it reaches a peak value, then, it immediately drops in a decelerated rate. The acceleration can be primarily attributed to the chemical reaction. The chemical reaction rate is relatively small when the fuel concentration is low at the initial stage. Along with the increased diffusion of fuel vapor, the reaction rate and temperature gradually increases, which further intensifies the gas phase reaction and fuel diffusion from the droplet surface. Consequently, the heat release rate and the gas phase temperature as well as the REG increase and accelerate after ignition. Our previous publication [16] has revealed that a rear flame will first form and gradually evolve to an envelope during the droplet combustion in such a low Reynolds number convective environment. For Case (a), it is found that the flame completely envelopes the droplet at t=4.5 ms, which corresponds to the moment associated with the maximum value of total REG in Fig. 2. Subsequently, the flame and its temperature distribution maintain the enveloping state. However, the droplet radius shrinks as it is depleted, and consequently, the REG also drops quickly. Similar unsteady REG variations were also reported by Hiwase et al. [12] and Lior et al. [13] for n-hexane and n-heptane droplet combustion in a quiescent gaseous environment, respectively. Hiwase’s results showed a much slower acceleration of REG before ignition and a flat variance before vanishing compared with our results, which may be attributed to the effects of the convective air flow, because the air flow significantly intensifies the heat and mass transfer between the phases as well as the diffusion in the gases.

Figure 2 also indicates that the increased free stream temperature [Case (b)] and velocity [Case (c)] have a significant effect on the total REG, both of which intensify the heat and mass transfer between thephases compared to Case (a). As a result, the ignition of combustion as well as the peak REG value is advanced. For Case (d) where the oxygen mass fraction in free stream is reduced from the normal value of 23% to 15%, while maintaining the other conditions the same as in Case (a), the ignition as well as the maximum value of the REG, is greatly postponed as a result of the deficiency of the reactant. The total REG over the droplet lifetime is determined by integrating the curves in Fig. 2 [using Eq. (4)]. Because the grid resolution is not good enough to accurately model the last ‘vanishing’ stage, only the results up to 7 ms out of the total approximately 8 ms lifetime [except Case (d)] are presented in Fig. 2, which are considered sufficient to reflect the thermodynamic characteristics. The integrated values from t=1 ms to 7 ms are 66, 59.9, and 61.9 J·K−1for Cases (a)-(c), respectively. Therefore, the results suggest that the increased velocity and temperature of the free stream will lead to a decrease of total entropy generation.

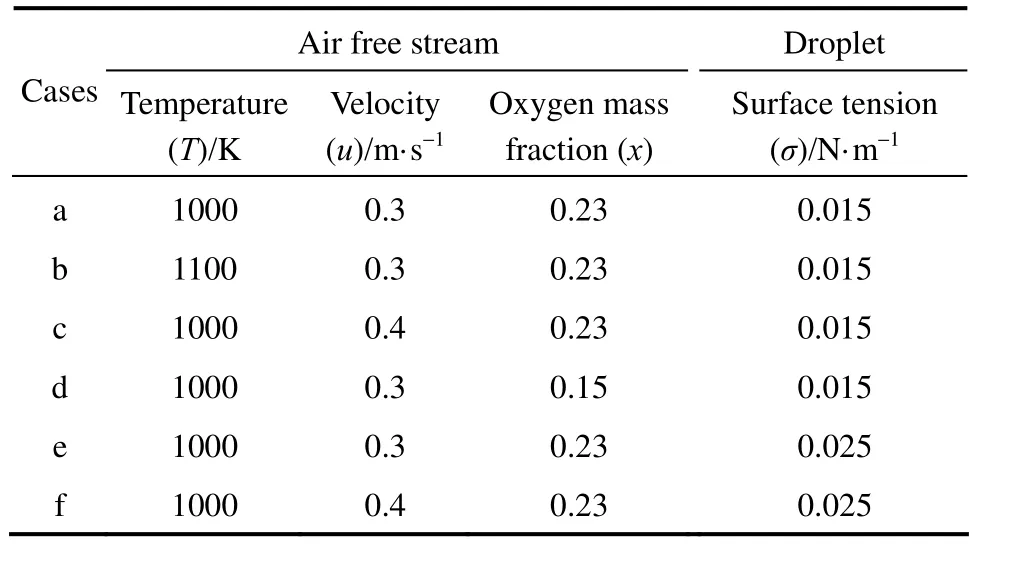
Table 1 Boundary conditions for the simulations of droplet combustion

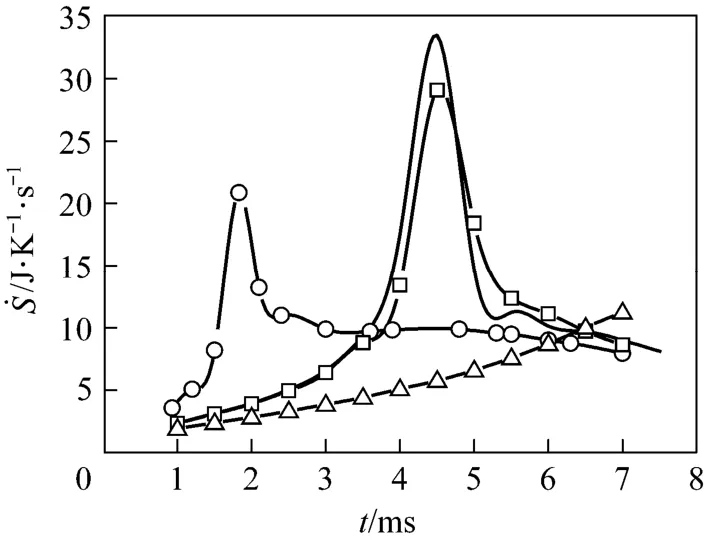
Figure 2 Temporal histories of total entr opy g enerate rate in the process of d roplet combustion in a con vective

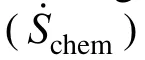
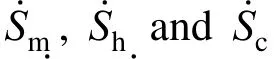
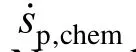
4.2 Effects of droplet deformation

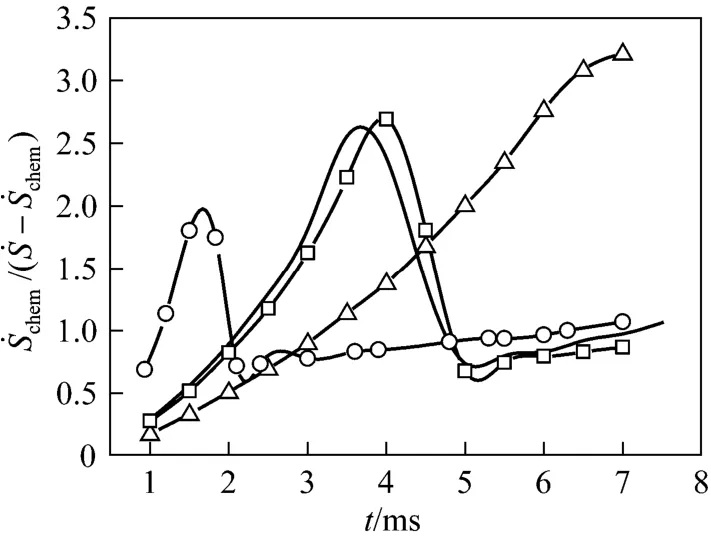
Figure 3 Temporal histories of the ratio of rat e of entropy generation due to chemical reaction to that due to transfer processes during the process of dr oplet combus-

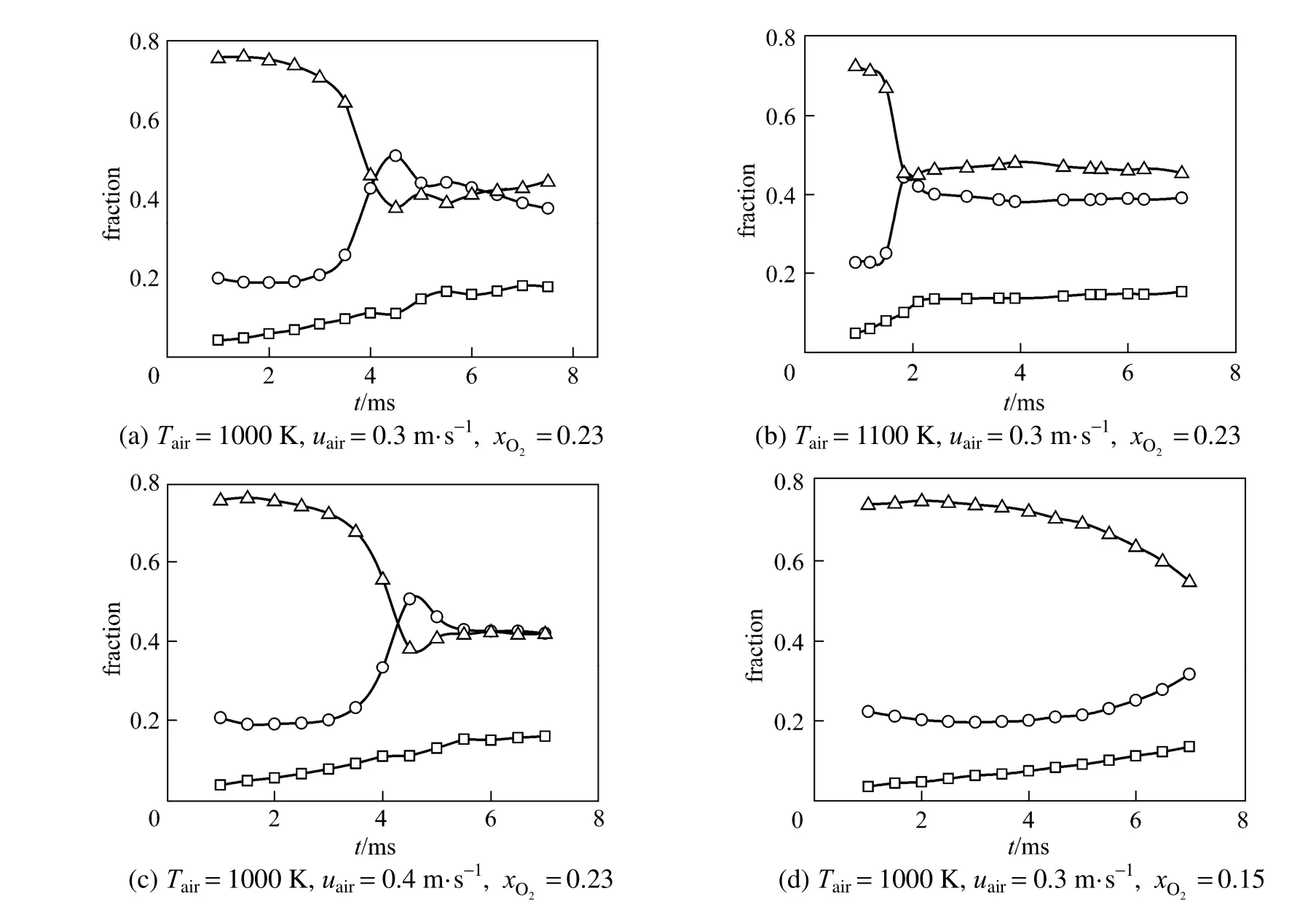
Figure 4 Temporal histories of the relative magnitude of the rate of entropy generation due to mass transfer, heat transfer and combined mass and heat transfer(di=0.1 mm, Ti=300 K, u0=0.05 m·s−1, σ=0.015 N·m−1)

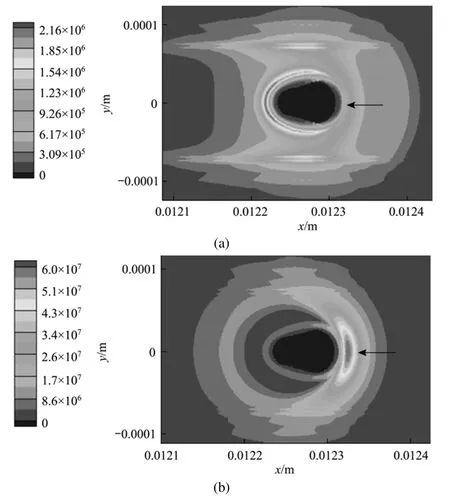
Figure 5 Entropy generation rate per volumep˙s distribution for Case (a) at t=6 ms due to (a) mass transfer, (b) heat transfer, (c) combined mass and heat transfer, (d) chemical reaction(Tair=1000 K, uair=0.3 m·s−1,2Ox=0.23, σ=0.015 N·m−1)

Figures 5 and 7 have clearly displayed the transition of a droplet to a sphere shape. Haywood et al. [8] has numerically demonstrated that during the combusting lifetime, the droplet shape will first change toan oblate shape with its major axis vertical to the mean flow direction, then to a prolate shape with its major axis parallel to the mean flow direction, and finally to an oblate shape again as the first stage nears its vanishing point. The deformation affects the surface temperature as well as the vaporization rate, and eventually the overall heat and mass transfer rates as well as the REG. The degree of deformation can be artificially controlled by changing the liquid surface tension, in order to inhibit the droplet from transforming into a sphere. Two cases [Case (e) and Case (f)] with the surface tension artificially increased to 0.25compared to the value of 0.15 used in Cases (a) and (c) are explored in order to investigate the quantitative effects of droplet formation on the REG.

Figure 5 Entropy generation rate per volumedistribution for case (a) at t=6 ms due to (a) mass transfer, (b) heat transfer, (c) combined mass and heat transfer, (d) chemical reaction

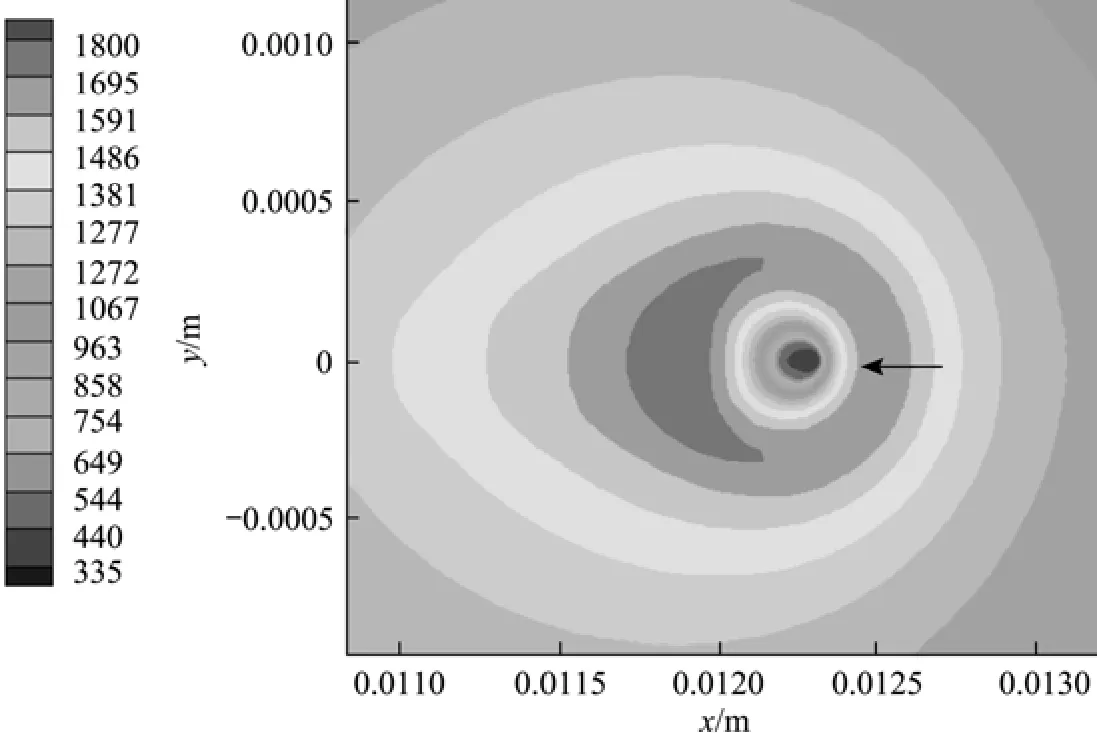
Figure 6 Temperature distribution for Case (a) at t=6 ms(Tair=1000 K, uair=0.3 m·s−1,2Ox=0.23, σ=0.015 N·m−1)

The results reveal that for a surface tension of 0.25, the aspect ratio (droplet axial length to transverse one) always approaches unity compared to the cases when the surface tension is 0.15. For example, the aspect ratio is 1.05 at t=6 ms for the larger surface tension, while it is about 1.5 for the smaller surface tension. Fig. 8 shows the transient histories of the total REG and its constitutions for Cases (e) and (f). For comparison, the curves of Cases (a) and (c) are also depicted. It can be observed that the deformation of the droplet leads to an increase in the maximum value of REG due to chemical reaction, but a decrease in REG due to heat transfer and combined mass and heat transfer. Changes in the REG due to mass transfer alone are negligible. The maximum value of the total REG remains almost the same for the two cases. Prior to the maximum, the total REG is a little bit smaller for the droplet with a smaller deformation, and the situation is reversed after the maximum. As a whole, the total REG is weakly dependent on the droplet deformation over the droplet lifetime for the modeling situations.

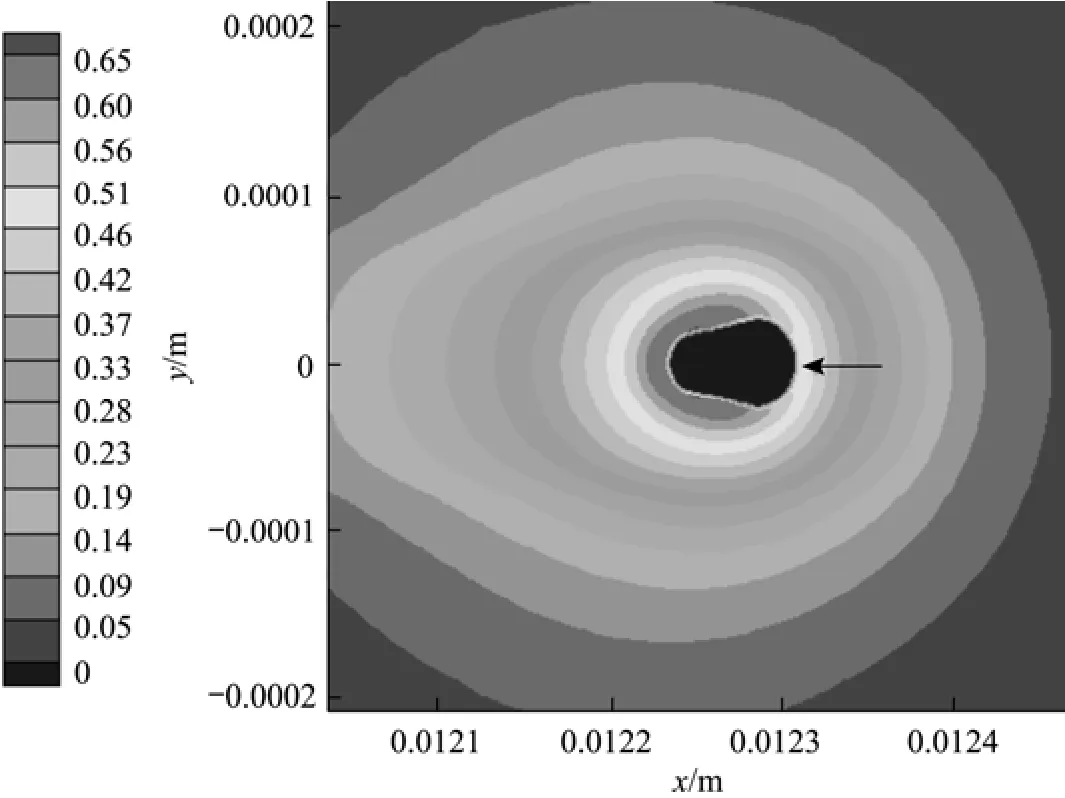
Figure 7 Decane mass fraction distribution for Case (a) at t=6 ms(Tair=1000 K, uair=0.3 m·s−1,2Ox=0.23, σ=0.015 N·m−1)

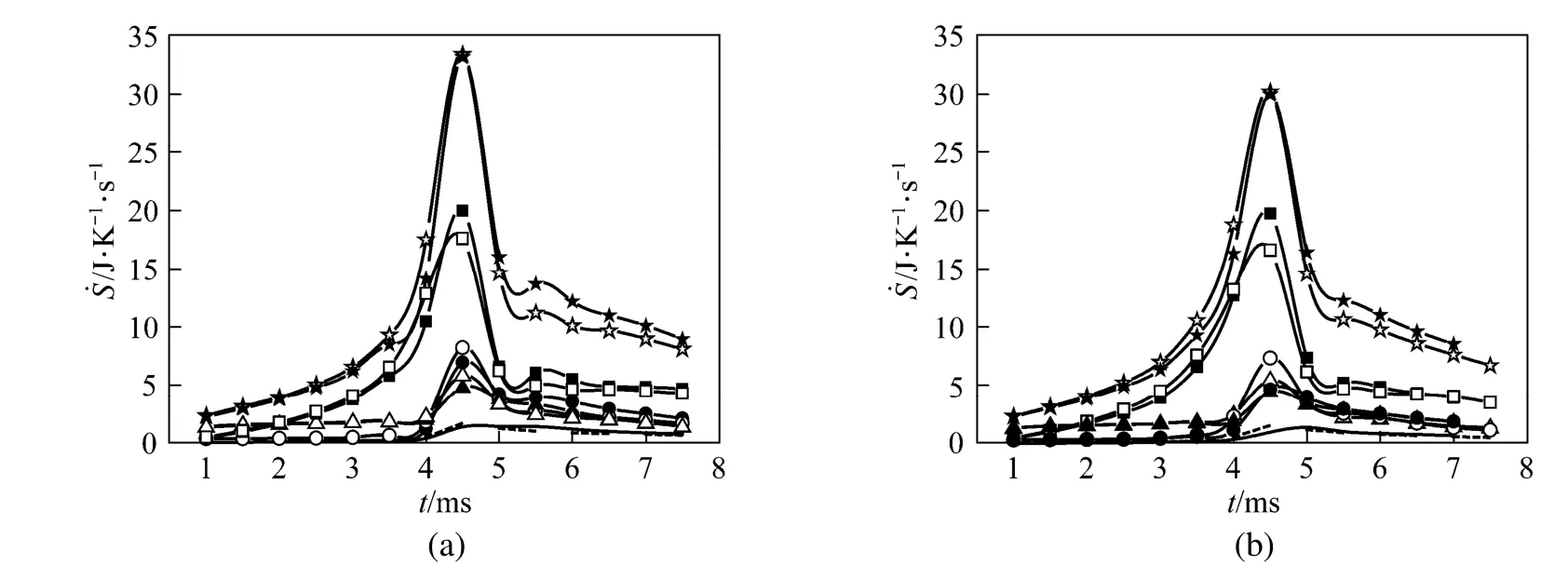
Figure 8 Temporal histories of total entropy generation ratio, and that due to mass transfercombined mass and heat transferfor (a) Cases (a) and (e), and (b) Cases (c) and (f)

5 CONCLU SIONS

This paper analyzed the entropy generation rate during the process of the decane droplet combustion in a high-temperature and forced-convective air flow. The analyses were based on the flow field calculations made previously at small Reynolds. The essential contributions due to the mass transfer, the heat transfer, the combined mass and heat transfer, and the chemical reaction are quantitatively determined. The following conclusions were drawn from the calculations and analyses:

(1) The entropy generation rate due to chemical reaction contributes most to the total entropy generation rate over the droplet lifetime. Entropy generationdue to mass transfer is insignificant; and entropy generation due to heat transfer and combined mass and heat transfer provide equivalent contributions.

(2) The large entropy generation rate due to the chemical reaction mainly results from the large chemical reaction area around the droplet. Therefore, in order to decrease the total entropy generation, a rear flame is preferred to an envelope flame because of the smaller area of coverage associated with the rear flame. A small initial Damkohler number less than the critical one is required to obtain an initial rear flame.

(3) The increases of the temperature and velocity of the free stream are preferred for droplet combustion at small Reynolds number (<1).

(4) The total rate of entropy generation is weakly dependent on the droplet deformation over the droplet combustion lifetime.

NOMENCLATURE

Cpspecific heat at constant pressure, J·kg−1·K−1

D diffusivity, m2·s−1

E˙dexergy destruction rate, J·s−1

Erchemical activation energy, Er=1.256×108J·kg-−1·mol−1for decane

h specific enthalpy, J·kg−1

Jmmass flux vector per area, kg·m−2·s−1

Jqheat flux vector per area, J·m−2·s−1

k thermal conductivity, W·m−1·K−1

M molecular mass

P pressure, Pa

S entropy generation rate, J·K−1·s−1

s specific entropy, J·kg−1·K−1

s˙pentropy generation rate per volume, J·m−3·K−1·s−1

T temperature, K

t time, s

v cell volume, m3

x molar fraction

y mass fraction

Δ rate of strain

λ stoichiometric coefficients

μcchemical potential, J·kg−1

σ stress tensors

ω chemical reaction rate, kg·m−3·s−1

REFERENCES

1 Som, S.K., Datta, A., “Thermodynamic irreversibilities and exergy balance in combustion processes”, Prog. Energy Combust. Sci., 34, 351-376 (2008).

2 Zhou, L.X., Li, K., Wang, F., “Advances in large-eddy simulation of two-phase combustion (I) LES of spray combustion”, Chin. J. Chem. Eng., 20 (2), 205-211 (2012).

3 Michael, J.M., Availability Analysis, Prentice Hall, New York, 45-83 (1989).

4 Puri, I.K., “Second law analysis of convective droplet burning”, Int. J. Heat Mass Transfer, 35 (10), 2571-2578 (1992).

5 Abramzon, B., Sirignano, W.A., “Droplet vaporization model for spray combustion calculations”, Int. J. Heat Mass Transfer., 32 (9), 1605-1618 (1989).

6 Renksizbulut, M., Haywood, R.J., “Transient droplet evaporation with variable properties and internal circulation at intermediate Reynolds numbers”, Int. J. Multiphase Flow, 14, 189-202 (1988).

7 Xu, G.W., Ikegami, M., Honma, S., Ikeda, K., Dietrich, D.L., “Interactive influence of convective flow and initial droplet diameter on isolated droplet burning rate”, Int. J. Heat Mass Transfer, 47, 2029-2035 (2004).

8 Haywood, R.J., Renksizbulut, M., Raithby, G.D., “Transient deformation and evaporation of droplets at intermediate Reynolds numbers”, Int. J. Heat Mass Transfer, 37 (9), 1401-1409 (1994).

9 Jog, M.A., Ayyaswamy, P.S., Cohen, I.M., “Evaporation and combustion of a slowly moving liquid fuel droplet: higher-order theory”, J. Fluid Mech., 307, 135-165 (1996).

10 Dash, S.K., Som, S.K., “Transport process and associated irreversibilities in droplet combustion in a convective medium”, Int. J. Energy Res., 15, 603-619 (1991).

11 Dash, S.K., Sengupta, S.P., Som, S.K., “Transport processes and associated irreversibilities in droplet evaporation”, J. Thermophysics, 5 (3), 366-373 (1991).

12 Hiwase, S.D., Som, S.K., “Entropy balance and exergy analysis o the process of droplet combustion”, J. Appl. Phys., 31, 1601-1610 (1998).

13 Lior, N., Wladimir, S.D., Hassan, S.A., “The exergy fields in transport processes: their calculation and use”, Energy, 31, 553-578 (2006).

14 Som, S.K., Dash, S.K., “Thermodynamics of spray evaporation”, J. Appl. Phys., 26, 574-584 (1993).

15 Pope, D.N., Raghavan, V., Gogos, G., “Gas-phase entropy generation during transient methanol droplet combustion”, Int. J. Therm. Sci., 49 (7), 1288-1302 (2010).

16 Zhang, X.B., Zhang, W., Zhang, X.J., “Modeling droplet vaporization and combustion with the volume of fluid method at a small Reynolds number”, J. Zhejiang Univ-Sci A: Appl. Phys. & Eng., 13 (5), 360-373 (2012).

17 Chiang, C.H., Raju, M.S., Sirignano, W.A., “Numerical analysis of convecting, vaporizing fuel droplet with variable properties”, Int. J. Heat Mass Transfer, 35, 1307-1324 (1992).

18 Wladimir, S.D., “Modeling and exergy analysis of a burning fuel droplet”, M.D. Thesis, Univ. Penn (2004).

19 Westbrook, C.K., Dryer, F.L., “Simplified reaction mechanisms for the oxidation of hydrocarbon fuels in flames”, Combust. Sci. Technol., 27, 31-43 (1981).

20 Wu, G., Sirignano, W. A., “Transient burning of a convective fuel droplet”, Combust. Flame, 157 (5), 970-981 (2010).

2012-05-24, accepted 2012-12-19.

* Supported by the National Natural Science Foundation of China (51276157) and the Natural Science Foundation of Zhejiang Province (LY12E060026).

** To whom correspondence should be addressed. E-mail: xuejzhang@zju.edu.cn