计及多重开关的电磁暂态仿真插值算法

刘 涛，闫贻鹏，金 娜，王旭东，林济铿

（1．天津市电力公司电力科学研究院，天津 300384；2．上海市电力公司青浦供电公司，上海 201700；3．上海市电力公司金山供电公司，上海 201500；4.同济大学电子与信息工程学院电力系，上海 201804）

计及多重开关的电磁暂态仿真插值算法

刘 涛1，闫贻鹏2，金 娜3，王旭东1，林济铿4

（1．天津市电力公司电力科学研究院，天津 300384；2．上海市电力公司青浦供电公司，上海 201700；3．上海市电力公司金山供电公司，上海 201500；4.同济大学电子与信息工程学院电力系，上海 201804）

为解决快速电磁暂态仿真程序中因多重开关动作易引起迭代震荡及仿真精度不高问题，提出一种能避免迭代震荡及具有较高精度的快速电磁暂态仿真插值新算法。该算法首先通过内插技术确定开关动作的准确时刻；然后从最近的开关动作时刻开始对本步长内该开关动作点之后的区间进行后向欧拉法试探积分；进而利用外插回推技术得到开关动作后的变量值作为下一步积分的初始值；最后进行一步梯形法积分并插值回到积分整步点，完成一个完整时步积分计算。算例证明本算法能避免迭代震荡并提高仿真精度，拥有应用前景。

插值技术；电磁暂态仿真；数值振荡；多重开关

目前，电力电子元件及设备在电力系统中的应用非常广泛。由于电力电子元件的快速多次反复动作特性造成了系统的网络拓扑结构也是随时间不断变化，且很可能在一个很短的时间内出现多个开关动作。如何准确地反映及捕捉各个开关动作给网络及系统带来的影响及现象，是所有电磁暂态仿真研究及程序开发所面临的挑战。

基于定步长积分技术而开发的EMTP程序是目前应用最为广泛的电磁暂态仿真程序[1，2]。在开关动作时，若实际开关动作时间出现在非整步点上，而积分过程却只能在整点上反映开关动作情况，往往造成开关动作点延迟，并且会出现非特征谐波[3-5]和数值振荡[6-10]。对于该问题，目前常采用的是插值算法[11-15]，即利用梯形积分中的分段线性化，在开关电流过零点时利用插值技术寻找到精确的开关动作时间。而对于在一个积分时步中包含有多个开关动作，即出现所谓的多重开关[16]时，当前的插值算法大都只是寻找一次开关动作或将多个动作近似到一个时间点上，从而不能准确反映实际情况，且也容易引起积分震荡。如何更准确地模拟多重开关动作问题一直是备受关注的课题。

本文首先对包含有多重开关的电磁暂态积分过程中的数值振荡和非特征谐波的产生机理进行理论分析；在此基础上，针对多重开关动作问题，提出了计及多重开关动作的插值新算法用于电磁暂态仿真积分计算，以消除仿真计算时出现的数值振荡和非特征谐波。

1 非特征谐波和数值振荡

EMTP等电磁暂态仿真程序均采用定步长的梯形积分法，从而只能计算整步点变量值。然而电力电子开关的动作点不一定出现在整步点上，以图1为例，当开关断开后，由于电感电流不能突变，二级管导通，在电感电流衰减至零时二极管关断，假设在td时刻二极管关断，如图2所示，则在第一个整仿真步长时刻（即图2中t-Δt）程序计算得到的二极管电流为正，二极管继续导通，在第二个整仿真步长时刻（即图2中时刻t）程序计算得到二极管电流为负，这个信息直到下一个整仿真步长时刻（即图2中t+Δt）才被处理，将二极管关断。而二极管电流实际上是在第一个仿真步长和第二个仿真步长之间的时刻（即图2中td）过零点。

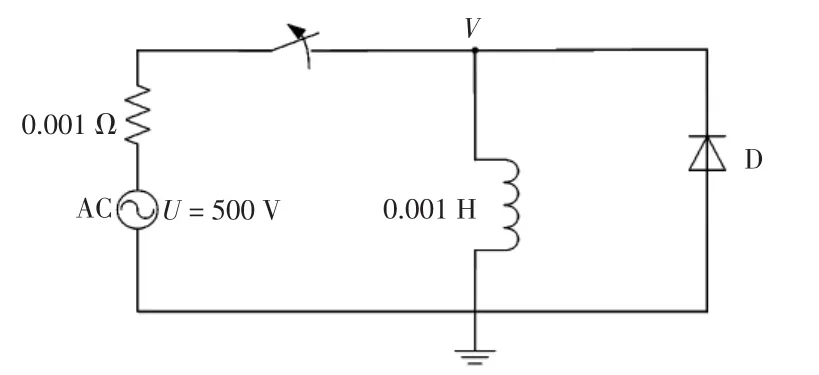
图1 简单电力电子开关电路Fig.1 Simple power electronic switch circuit

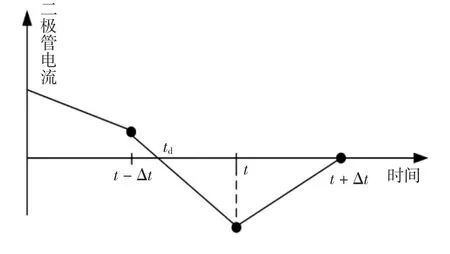
图2 固定步长仿真时开关动作示意Fig.2 Switch action schemes at fixed-step simulation

程序中开关动作时间上的延迟将造成电压电流波形出现不真实的“尖峰”，即非特征谐波。因此，只有找到真正的开关动作点，让仿真中电子开关的动作回归到正确时刻才能消除非特征谐波。

对于图1中电感支路，其梯形法积分公式为

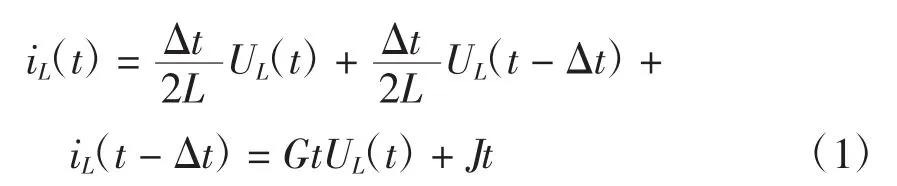
如果开关在td时刻动作，电压u将发生突变，即UL（td-）≠UL（td+），在仿真中应以td+时刻的变量求解td+Δt时刻的值，但实际计算时常用td-时刻非状态变量值计算等值电流源，而由于UL（td-）≠UL（td+），这就造成了数值震荡。

目前常采用向后欧拉法消除数值震荡，向后欧拉法的公式为

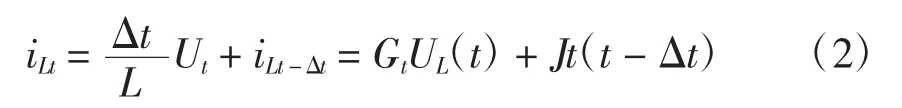
从式（2）可看出，该方法避免了非状态突变量UL（td-）的影响，因此能够彻底地消除数值震荡。

2 新的插值算法

以上分析可知，要仿真电力电子元件的动作过程，首先要寻找到正确的开关动作点，然后采用向后欧拉法，从而既能消除震荡产生，又能正确反应开关动作。基于此思想，同时考虑到快速仿真中往往需采用大步长而导致一个积分时步中可能包括多重开关动作，本文提出一种新的插值算法，既能对多重开关的开断准确反映，又能避免震荡。

算法的核心思想是，在从t积分到t+Δt时刻时检测到开关动作td，以t和t+Δt时刻的变量插值到td，得到td（0-）变量，接着检查在td到t+Δt直接是否有开关动作，若有则以td和t+Δt为基准插值到新的开关动作点td′，再从新的开关动作点用一步1%的向后欧拉法以消除振荡，再通过外插回推得到td（0+）时刻的变量，最后回到整步点，开始下一时步的仿真积分。具体过程如下：

（1）由t-Δt时刻使用一步梯形法积分法到t；

（2）由t时刻使用一步梯形法积分法到t+Δt，此时检测到td时刻开关动作；

（3）由t和t+Δt时刻内插到td时刻值；

（4）改变开关状态，重新形成导纳矩阵，从td时刻以步长为t+Δt-td的向后欧拉法积分到t+Δt时刻，检测td到t+Δt之间是否还有开关动作，若有则由td和t+Δt时刻内插到新的开关动作点，重复步骤（4），若没有，则转入步骤（5）；

（5）在td时刻，用向后欧拉法以1%步长积分一步到td+Δt/100；

（6）由td+Δt/100和td时刻值外插到td-Δt/100时刻值；

（7）在td+Δt/100时刻以1%步长的向后欧拉法积分一步到td；

（8）在td时刻以1%步长的向后欧拉法积分一步到td+Δt/100；

（9）在td+Δt/100时刻用一整步梯形法积分至td+Δt/100+Δt；

（10）由td+Δt/100和td+Δt/100+Δt时刻值内插到t+Δt整步时刻，恢复正常梯形法积分直到检测到下一个开关动作点。插值变化过程如图3所示。

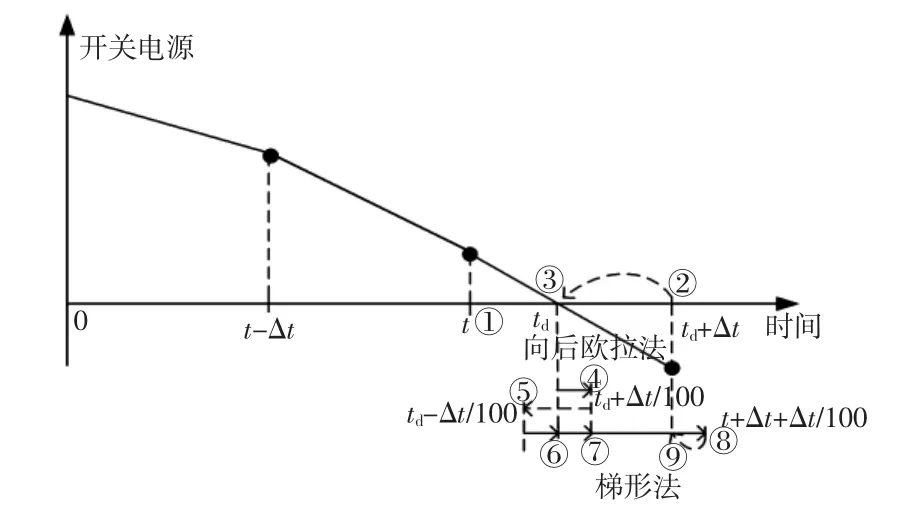
图3 新插值算法的插值变化过程Fig.3 Interpolating process for the new interpolationextrapolation algorithm

上述插值算法的解释和说明：

（1）第（3）步通过内插技术得到开关动作前的变量值；第（4）步进行因开关动作而进行相应的网络拓扑改变；第（4）步继续寻找本步长内的其他开关动作点，并插值到新的开关动作时刻同时改变拓扑结构，直到找到最后一个开关动作点为止；第（5）步利用1%步长的向后欧拉法消除振荡；第（6）、第（7）步利用外插回推过程得到开关动作后的变量值，即td（0+）时刻值；第（8）步利用td（0+）时刻的值向前积分，避免了td（0-）值的影响；第（9）、第（10）步利用内插技术插值到整步点上，完成下一步梯形法积分的准备。

（2）在上述算法第（4）步中，采用了试探检测来寻找同一步长内的多次开关动作，且每次寻找到一个新动作点都进行内插计算和网络拓扑改变，虽要多花去一部分计算时间，但通过该操作后能准确寻找到每一次开关动作时刻，从而为下一步积分提供正确的初始状态，可明显提高仿真精度。

（3）因电磁暂态仿真精度取决于数值积分方法和步长，梯形积分法的精度为二阶，向后欧拉法精度为一阶，因此在第（5）步中采用1%步长向后欧拉法，相比文献[12，13]中采用的半步长向后欧拉法策略既能消除振荡且精度更高。同时，本方法回到了整步点输出，能与导纳矩阵和暂态模型相匹配。由于本方法将计算得到的td（0+）时刻值用于下一步积分，相比文献[14]获得了更加精确的初始值，故总体仿真结果也具有更高精度。

（4）本文方法相对于非插值算法，相同步长下计算时间较长。但相对于插值类算法，虽计算量略有增加，但增加的不大。本文方法的突出优点是具有较高的仿真精度和稳定性，虽有一定的计算量增加，但相对于现在计算机的计算能力，这样的增加几乎可以忽略不计。

3 算例

3.1 算例1

如图1所示，在开关断开后，二极管导通为电感续流，当电感电流为零时二极管关断。分别利用文献[13，14]和本文插值法对该过程进行电磁暂态仿真，给出二极管关断时电压V的波形，并与10 μs步长仿真时的电压波形对比，如图4和图5所示，其中图4采用50 μs步长，图5采用100 μs步长。

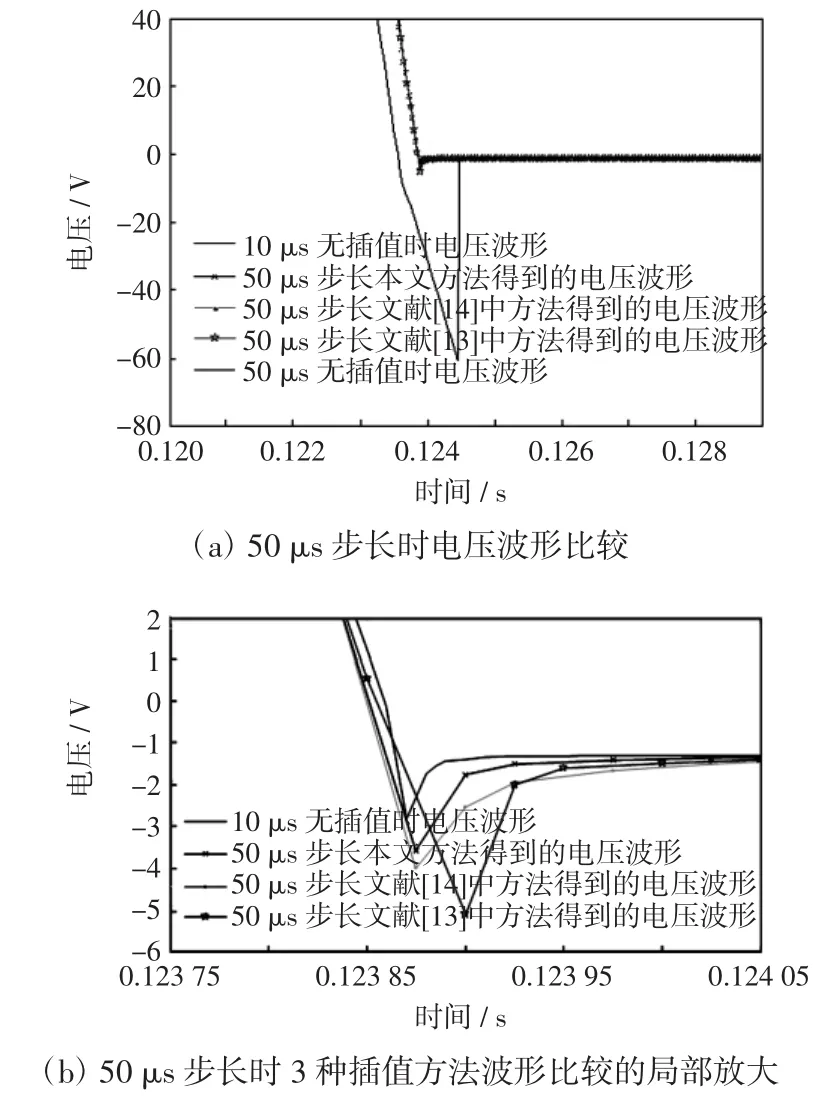
图4 50 μs步长时电压波形比较Fig.4 Comparison of the voltage waveforms at 50 μs time-step

通过图4（a）和图5（a）比较可知，50μs和100μs步长时，不利用插值算法的仿真结果误差很大，而利用插值算法后的仿真波形接近10 μs仿真结果，说明插值技术对程序的精度有很大提高。

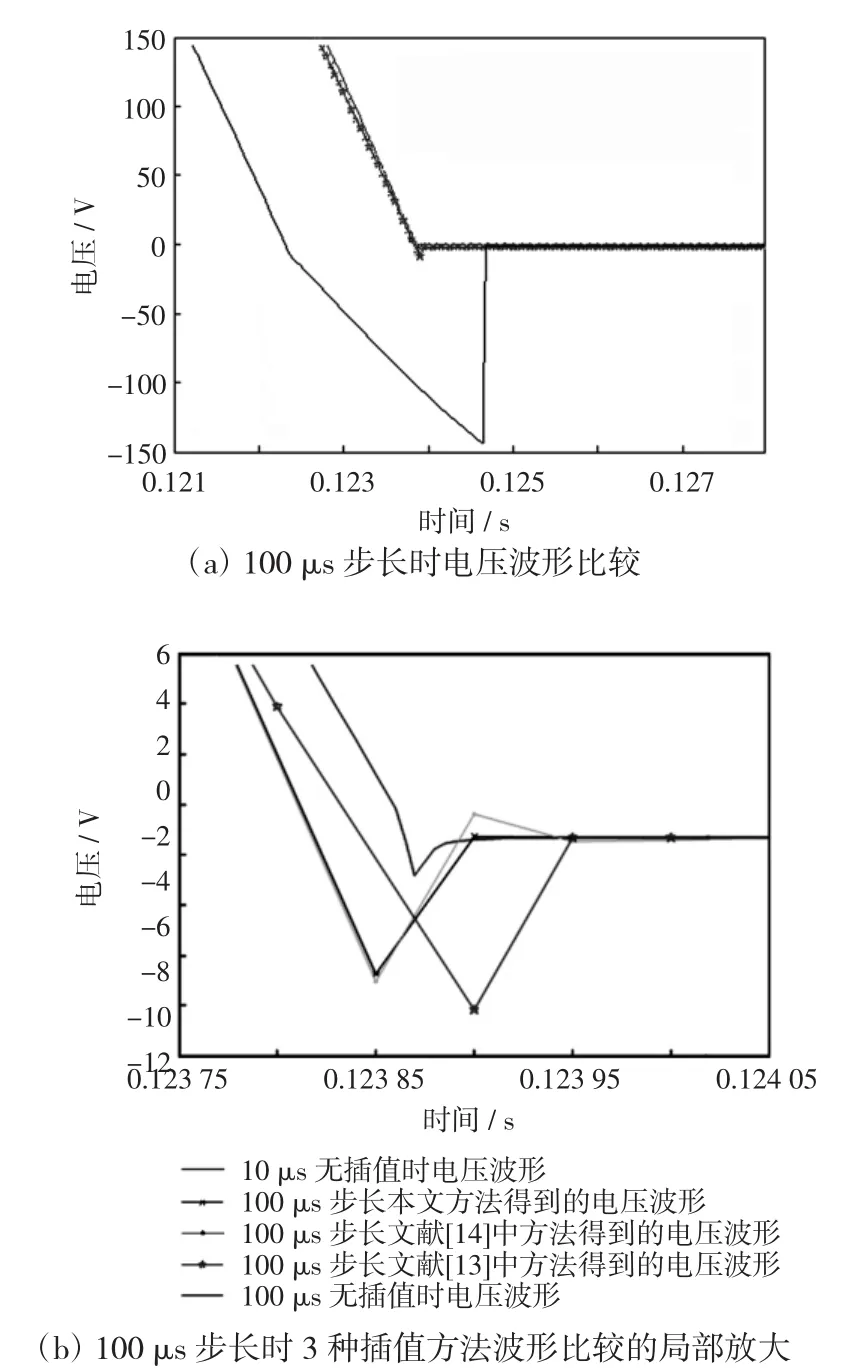
图5 100 μs步长时电压波形比较Fig.5 Comparison of the voltage waveforms at 100 μs time-step

由图4（b）和图5（b）可看出，本文提出的新插值方法相比文献[13]，[14]的方法更接近于10 μs的仿真结果。从而也证明本文方法相较其他方法具有更高的仿真精度和更好的数值稳定性。

3.2 算例2

算例2为一完整整流逆变电路，如图6所示。有4个换流器，24个电力电子开关元件，并包含分布式参数线路，滤波器等元件。在这个电路中，开关动作不仅包括自然换相也包括强制换相，而且用大步长仿真时会出现多重开关问题。本文采用频率50 Hz，仿真步长分别为50 μs和100 μs，整流侧触发角α=15°，逆变侧β=45°，仿真时间为1 s，测量长线路中靠近整流侧端的电压值。

图7和图8分别给出了50 μs和100 μs步长时本文插值方法、文献[13]，[14]中的插值方法以及没有插值时的电压曲线。可看出利用插值方法后，直流电压的振荡较少、波形平稳，说明3种插值方法对于开关动作引起的振荡有很好消除。然而，本文方法相对于文献[13]，[14]方法得到的波形更加平稳，说明在包含多个开关动作的系统仿真中，本文方法更好地消除了数值振荡和非特征谐波，具有更好的仿真精度和数值稳定性。同时从图7和图8的比较可知，步长从50 μs增加到100 μs时，对于本文插值方法得到的波形平稳度基本不受影响，说明本插值方法在大步长时仍适用，即对于大步长的电磁暂态仿真依然保证了一个较高精度，从而适用于大系统快速电磁暂态仿真。

图6 整流逆变系统图Fig.6 Rectifier inverter system

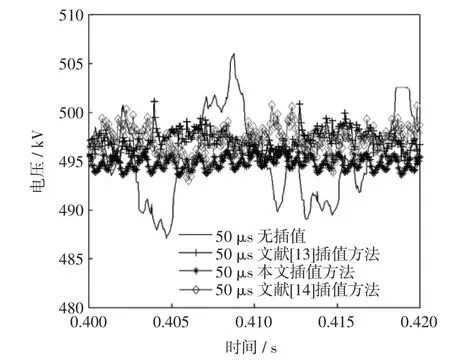
图7 50 μs步长时直流电压比较Fig.7 Comparison of DC voltage waveforms at 50 μs time-step

图8 100 μs步长时直流电压比较Fig.8 Comparison of DC voltage waveforms at 100 μs time-step

4 结语

针对快速仿真中多重开关的问题，本文提出一种适用于快速电磁暂态仿真的插值新算法。该方法的特点是通过内插技术寻找正确的开关动作点，采用试探法寻找一个步长内的多次开关动作，利用1%步长的向后欧拉法有效消除了数值振荡；并利用外插回推技术得到正确的网络拓扑结构和积分初始值。算例表明，本文算法相较于其他方法在处理多重开关时，既能更好地避免数值震荡，又有更高的仿真精度。算例也表明，本文算法在较大积分步长时，仍具有较高的数值稳定性和精度，从而拥有实际工程应用的前景。

[1]Dommel H W．Digital computer solution of electromagnetic transient in single and multiphase networks[J]．IEEE Trans on Power Apparatus and Systems，1969，88（4）：388－399．

[2]De Kelper B，Dessaint L A，Al-Haddad K，et al．A comprehensive approach to fixed-step simulation of switched circuits[J]．IEEE Trans on Power Electronics，2002，17 （2）：216－224．

[3]Watson N，Arrillaga J．Power Systems Electromagnetic Transients Simulation [M]．London：The Institution of Electrical Engineers，2003．

[4]王成山，高毅，王丹，等（Wang Chengshan，Gao Yi，Wang Dan，et al）．考虑直流系统开关特性控制的变步长仿真算法 （Variable-step simulation method considering HVDC controls with switching characteristics）[J]．中国电机工程学报（Proceedings of the CSEE），2009，29（34）：16-21．

[5]刘文焯，汤涌，侯俊贤，等（Liu Wenzhuo，Tang Yong，Hou Junxian，et al）．考虑任意重事件发生的多步变步长电磁暂态仿真算法（Simulation algorithm for multi variable-step electromagnetic transient considering multiple events）[J]．中国电机工程学报（Proceedings of the CSEE），2009，29（34）：9-15．

[6]张益，周群（Zhang Yi，Zhou Qun）．电力系统数字仿真中的数值振荡及对策（Numerical oscillation and its counter measures in power system simulation）[J]．上海交通大学学报（Journal of Shanghai Jiaotong University），1999，33 （12）：1545-1549．

[7]应迪生，张明（Ying Disheng，Zhang Ming）．动态相量法仿真中的数值振荡及消除（Elimination of numerical oscillation in power system simulation using dynamic phasor）[J]．电力系统及其自动化学报（Proceedings of the CSU-EPSA），2007，19（4）：41-45，128.

[8]刘益青，陈超英（Liu Yiqing，Chen Chaoying）．用以消除数值振荡的阻尼梯形法误差分析与修正（Error analysis and correction of damping trapezoidal integration for eliminating numerical oscillation）[J]．中国电机工程学报（Proceedings of the CSEE），2003，23（7）：57-61．

[9]Lin Jiming，Marti J R．Implementation of the CDA procedure in the EMTP[J]．IEEE Trans on Power Systems，1990，5（2）：394-402．

[10]Marti J R，Lin J．Suppression of numerical oscillations in the EMTP power systems[J]．IEEE Trans on Power Systems，1989，4（2）：739-747．

[11]Kuffel P，Kent K，Irwin G．The implementation and effectiveness of linear interpolation within digital simulation[J]．International Journal of Electrical Power and Energy Systems，1997，19（4）：221-227．

[12]Zou Ming，Mahseredjian Jean，Joos Geza，et al．Interpolation and reinitialization in time-domain simulation of power electronics circuits[J]．Electric Power Systems Research，2006，76（8）：688-694．

[13]王成山，李鹏，黄碧斌，等（Wang Chengshan，Li Peng，Huang Bibin，et al）．一种计及多重开关的电力电子时域仿真插值算法（An interpolation algorithm for time-domain simulation of power electronics circuit considering multiple switching events）[J]．电工技术学报（Transactions of China Electrotechnical Society），2010，25（6）：83-88．

[14]Hong S N，Liu C R，Bo Z Q，et al．Elimination of numerical oscillation of dynamic phasor in HVDC system simulation [C]//IEEE Power&Energy Society General Meeting.Calgary，Canada：2009．

[15]王勇，赵锦成，解璞（Wang Yong，Zhao Jincheng，Xie Pu）．基于PSCAD/EMTDC的开关元件的暂态仿真算法研究（Study on transient simulation algorithm of switching element based on PSCAD/EMTDC）[J]．电气开关（Electric Switchgear），2008，5（5）：17-18．

[16]Faruque M O，Dinavahi Venkata，Xu Wilsun．Algorithms for the accounting of multiple switching events in digital simulation of power-electronic systems[J]．IEEE Trans on Power Delivery，2005，20（21）：1157-1167．

Interpolation Algorithm for Electromagnetic Transient Simulation Considering Multiple Switching Events

LIU Tao1，YAN Yi-peng2，JIN Na3，WANG Xu-dong1，LIN Ji-keng4
（1.Electrical Power Research Institute of Electrical Company of Tianjin，Tianjin 300384，China；2．Qingpu Power Supply Branch of Shanghai Municipal Electric Power Company，Shanghai 201700，China；3.Jinshan Power Supply Branch of Shanghai Municipal Electric Power Company，Shanghai 201500，China；4.Department of Electrical Engineering，College of Electronic and Information Engineering，Tongji University，Shanghai 201804，China）

Due to the iteration oscillation and low precision frequently resulted from multiple switching events in electromagnetic transient program，a new interpolation algorithm to solve these problems is presented in the paper.Interpolation technology is applied to find the accurate switching time.The trial backward Euler integration method，considering multiple switching action during the simulation，is then utilized to integrate interval followed the latest action from switching action in current step.Extrapolation and back-ward technology are combined to obtain the variable value after switching points.Thus a correct topology and initial values for the next integration are achieved.Finally，a step of trapezoidal integration combined with interpolating is further proceeded to be back to the integer step point.The results of the samples demonstrate the validity of the proposed algorithm.

interpolation technology；electromagnetic transient simulation；numerical oscillation；multiple switching

TM711

A

1003-8930（2013）06-0143-05

刘 涛（1980—），硕士，工程师，从事电力系统仿真及继电保护试验工作。Email：net_liutao@126.com

2013-04-22；

2013-05-18

阎贻鹏（1987—），硕士，助理工程师，从事电力系统仿真分析工作。Email：yyp1125018@126.com

金 娜（1986—），硕士，助理工程师，从事电力系统仿真分析工作。Email：Jinna198777@163.com