改进GAAA算法在多目标电网规划中的应用

孔祥聪，周步祥，汝锐锐，肖 贤，叶宗斌

（四川大学电气信息学院，成都 610065）

改进GAAA算法在多目标电网规划中的应用

孔祥聪，周步祥，汝锐锐，肖 贤，叶宗斌

（四川大学电气信息学院，成都 610065）

针对多目标电网规划中多维变量问题，该文采用GAAA算法对多目标电网规划的应用进行建模。建立了能够描述电网经济性、可靠性、N-1静态安全的多维动态规划模型。为改善GAAA算法的性能，对该算法分别进行了种群初始化、信息素更新精英策略、变量离散化和越界处理等措施的改进，提高了GAAA算法的收敛性和寻优效率。试验中，通过对一个46节点系统进行测试，该计算结果证明了改进的GAAA算法能有效地解决电网规划含离散性变量的多维组合优化问题。

多目标电网规划；全局寻优；收敛性；离散性变量；GAAA

当今社会，电能是我国社会的重要能源。随着人们对电能需求的增加，电力系统现有的网架结构不能更好地满足电力传输与分配。为此，如何提高电网规划的水平成为了一个重要的研究课题。电网规划具有多目标性、动态性等特点，它需要综合考虑可靠性、经济性、安全性等各种因素。目前，针对多目标电网规划，国内外学者在仿电磁学算法（ELM）、遗传算法GA（genetic algorithm）、粒子群PSO（particle swarm optimization）算法、蚁群AA（ant algorithm）算法等做了深入研究[1～8]。这些算法虽然能使多目标电网规划中的寻优决策、资金投入得到最佳，但是也存在一定的局限性，如有些算法只能局限于单阶段电网规划、目标函数冲突、收敛性差等。为此，本文以此为基础对算法进行改进，并将改进GAAA算法用来解决所建立的多目标电网规划模型。

本文针对多目标遗传算法（GA）、蚁群算法（AA）在电网规划中的应用进行改进，采取的改进策略弥补了基本算法的缺陷，提高了大规模离散组合优化问题的寻优能力。然后利用所建立的模型进行求解，并用46系统节点进行测试，验证了GAAA算法的有效性。

1 电网规划的数学描述

1.1 问题的一般描述

电网规划问题的一般描述为：设电网规划中需优化的目标数为m，且它们之间存在相互抵触的目标函数。其中，假定f1（X），…，fr（X）要求最大化，fr+1（X），…，fm（X）要求最小化，为了处理方便，把各目标函数转化为最小化问题。将最大化目标函数转换为最小化目标函数后，构成的新目标函数形式可表示为

1.2 极值求解问题

设F（X）为n维欧式空间En的区域R上的n元函数，其中X=（x1，…，xn），X∈R。若存在某个ε＞0，对于 X*∈R，当‖X-X*‖＜ε时均满足f（X）≥f（X*），则称X*为f（X）在R上的局部极小点，f（X*）为局部极小值。

若点X*∈R，而对于所有X∈R都有f（X）≥f（X*），则称X*为f（X）在R上的全局极小点，f（X*）为全局极小值。

1.3 Pareto最优方案

多目标优化问题Pareto最优解[9]描述为：当X*为最优解时，即表示∀X∈R（决策空间），有f （X*）≥f（X）；当X*是非劣解时，即不存在X∈R，有f（X）≥f（X*），即至少有一个分量，满足“＞”才成立。这种非劣解在多目标电网规划中常称为Pareto最优解，由意大利经济学家Villefredo Pareto于1896年提出。可描述为：对于式（1）的多目标优化问题，R为决策空间，对于∀X∈R，不存在下述情形时，称X*为Pareto最优解，即

式中：符号“≻”表示优于。

2 多目标电网规划模型

2.1 目标函数

传统电网规划模型一般只考虑经济性，忽略了可靠性、安全性。随着近年来全国各地电力事故的发生，需要综合考虑可靠性、经济性和安全性的重要性日益明显。为此，本文以多目标电网规划问题的一般最优化模型为基础，分别建立了经济性最优、可靠性最优、安全性最优为主要的目标函数。GAAA算法求解多目标电网规划数学模型为

式中：λ1、λ2、λ3为对应信息素的权重，且λ1+λ2+ λ3=1，Xl为第l规划阶段的方案；单位功率损耗的电网投资成本Cl（Xk）能反映经济性多少；电网运行成本CO（Xl）、维护成本CR（Xl）能反映可靠性高低；缺电成本能反映安全性大小；C（X）为成本变量；Wl、Tl为第l中负荷水平的概率和负荷持续时间；Ip为缺电损失评价率；Lq，l为正常状态的切负荷量；Wqt为故障停运率。η（k）为待建线路条数，且有

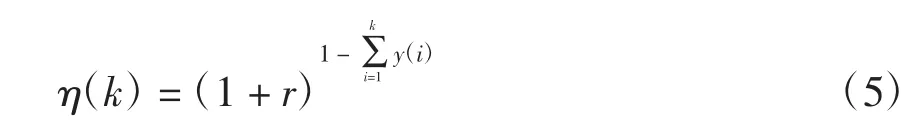
2.2 约束条件

3 改进GAAA算法的实现

3.1 GAAA的基本原理

GAAA算法实质上是GA（遗传算法）和AA（蚁群算法）结合在一起，与单一的GA算法和AA算法不同的是，GAAA算法在搜索过程中。不同的路径产生的信息素对应多目标电网规划中的可靠性、经济性、安全性目标函数，然后结合这些目标函数建立一个适应值函数。在寻优过程中，要确保可靠性、经济性、安全性地位相同，这样才能使蚂蚁等概率搜索。再对种群信息素进行局部更新和全局更新，使蚂蚁朝着可靠性、经济性、安全性最优方向优化，并把每一次的解存放在Pareto最优解集中，不断的迭代求解得到最优解。

3.2 算法改进策略

3.2.1 种群初始化

为使初始蚂蚁产生的信息素满足控制变量的约束条件，将不同蚂蚁产生的信息素X作为控制变量，即

然后随机生成μ组标准正态随机系数Xm′，即

式中，μ为蚂蚁数。

最后形成初始种群为

反复运用式（14），可得到由m×n个体所构成的整数矩阵Am×n。该过程使用了均概率的使用方法，因此能够保证种群初始化对解域的覆盖率，及其分布性和多样性，这为算法更快地寻得全局最优解创造了条件。

3.2.2 信息素更新精英策略

为保存蚁群的优良品质和提高算法的收敛效率。将能找到最优路径的蚂蚁称谓精英蚂蚁，并增大释放的信息素数量。信息素的更改公式为

式中：Q为精英蚂蚁在本次循环中留下的单位长度的信息素量，为常数；L*为精英蚂蚁在循环中所走过的路径长度；τij（t+1）为边z（x，y）信息素强度；ρ表示在时间间隔（t，t+n）内信息量衰减的系数。Δτij（t，t+1）为蚂蚁m在边z（x，y）上单位长度的信息素增量；z（x，y）为本次循环中的部分最优解；δ为精英蚂蚁的个数。

3.2.3 变量离散化及越界处理

多目标电网规划问题是一个含有很多离散变量的组合优化问题，文献[10]只能解决连续变量。因此，需要对全局更新的新变量进行离散化处理[10]，即

式中：τij为信息素强度；M为搜索路径步长。

对于离散变量不满足取整条件的信息素，采用四舍五入；对于越界的信息素，若越出上/下界，则分别取其为上/下界。在整个处理过程中都采用等概率搜索方法，这种方法不仅满足决策变量的约束条件及离散化特点，还维持了种群的多样性，也符合GAAA算法的基本原则。

3.2.4 收敛性判定

当以给定的信息素增量作为收敛判据时，设置的信息素增量过大，将降低算法的效率；信息素增量过小，将不能获得全局最优解。因此，为避免算法受阻于局部极值点，本文采用信息素增量和种群性能差异相结合的双判据方式，作为算法的收敛性判定。即在给定的信息素增量范围内，当种群中各蚂蚁与最优蚂蚁之间的信息素差异不大于给定正数ε时，则认为算法已收敛。

3.2.5 求解步骤

（1）根据求解的优化问题设置基本参数，如初始种群有m个体及个体变量数为n等参数；

（2）种群初始化，即形成矩阵形式解域Am×n；

（3）对当前的各蚂蚁进行局部自适应搜索，并进行更新；

（4）利用GAAA算法计算各蚂蚁的信息素增量Δτij、信息素xi(t)、变异量ρi(t)等；

（5）由精英策略蚁群算法挑选出新一代的种群，计算各蚂蚁的信息素Δτij（t，t+1），并进行存储；

（6）根据式（17）判断寻优过程是否收敛。若收敛，则输出Δτij*（t，t+1）最优解；否则，转至（7）；

（7）判断进化代数是否满足最大停滞代数。若不满足，则在依次施行（8）和（9）后，转至步骤（3）；若满足已设定的停滞代数，则输出“计算不收敛”；

（8）对种群实施精英策略；

（9）对种群进行自适应变异。

4 算例分析

本文在已知规划水平年负荷预测和电源规划的基础上，选择的主要测试对象为46节点的可行系统，仿真运算时的测试平台为Matlab（R2009a）和电力系统潮流计算软件BPA（bonneville power administration）。该系统在规划基础年共有46个节点、76回线路，其网络结构如图1所示，规划年的节点数、线路数及线径等参数主要根据大用户+自然增长率负荷预测获得。测试前，对系统所取的功率基准值SB=100 MVA。限于篇幅，各节点和负荷仍然沿用文献[11]中的数据。经济性和可靠性的指标参数如表1所示，参数信息可参阅文献[12]。在该系统中，每个规划阶段实施完成前后，都需保证网络既定的连通性。

图1 46节点系统的拓扑结构Fig.1 Topology of the 46-bus system

表1 46节点系统的经济性和可靠性指标Tab.1 Economic and reliable parameters of the 46-bus system

为校验本文所确立的权重系统（或模型归一化方法）的优越性，应用文献[13]中的线性加权法对多目标进行协调。为校验该方法的可行性，将人为选取的权系统与其进行了对比，具体比较情况列于表2中。其目标是在安全运行的前提下，根据优化的网架结构、负荷情况寻求一组最优的权重比例。

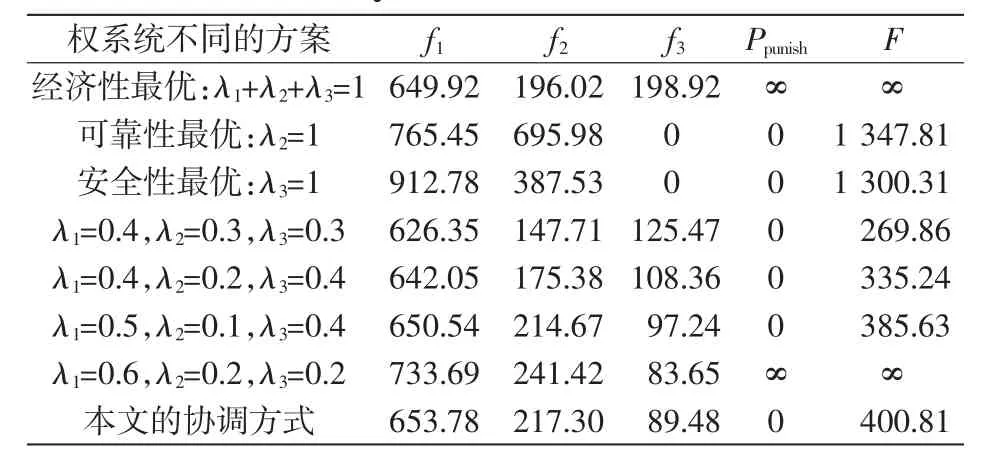
表2 46节点系统不同权系统的规划结果Tab.2 Different weights planning results of the 46-bus system

根据表2可知，文献[13]中的线性加权法不受限于目标函数的个数，适合解决大规模电网规划问题，用GAAA算法求解文中所构造的多目标电网规划模型，求得的单方面最优规划方案不具有较高的综合满意度，更不是最优规划方案。另外，因为规划方案的经济性仍然是其主要约束，故而采用GAAA算法所得的解，与只考虑经济性模型时所获得的最优规划方案相比，本文采用的权系统协调方式能使全局最优解在满足经济性约束的同时，也获得了较高的可靠性，体现了规划方案的综合社会效益。

为验证GAAA在多目标动态电网规划问题应用中的有效性，令权重系统为λ1=0.5，λ2=0.2，λ3=0.3时，采用GA、AA以及GAAA算法，对46节点系统进行求解。其运行对比结果如表3所示。

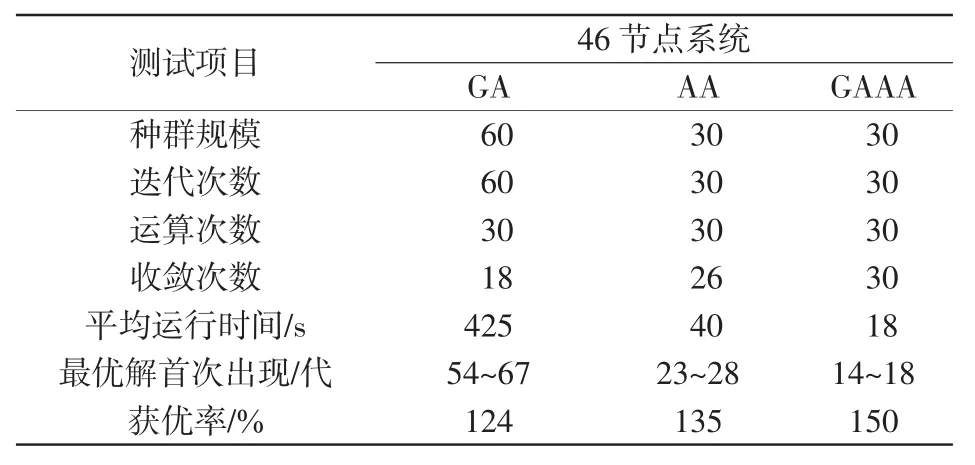
表3 算法性能对比Tab.3 Comparison of algorithm performance

根据表3的仿真比较可知，GAAA算法比GA算法能够很好地解决电网规划多目标的归一化问题，所提供的经济性、可靠性、安全性的变权重值，可以使规划人员灵活地根据实际情况决策优化控制方案。从对比结果中还可以看出，GA算法在解决多目标动态电网规划时，仅需较少的种群规模和迭代次数。通过算法对比，GAAA算法更适于求解多目标、非线性、多峰值、高维数的大规模离散组合优化问题。

5 结论

（1）GAAA算法是一种新型的全局优化算法，自身携带的参数少，操作方便，收敛性好。

（2）本文所提出的模型能较为理想地处理经济性、可靠性、安全性三者之间的关系。

（3）本文引入种群初始化、信息素更新精英策略、变量离散化和越界处理、收敛性判定等改进措施，克服了算法的缺陷，提高了收敛性和寻优效率。

[1]付锦，周步祥，王学友，等（Fu Jin，Zhou Buxiang，Wang Xueyou，et al）．改进仿电磁学算法在多目标电网规划中的应用（Application of improved electro magnetismlike mechanism in multi-objective power network planning）[J]．电网技术（Power System Technology），2012，36 （2）：141-146.

[2] 符杨，孟令合，胡荣，等（Fu Yang，Meng Linghe，Hu Rong，et al）.改进多目标蚁群算法在电网规划中的应用（Application of improved multi-objective ant colony algorithm in power network planning）[J].电网技术（Power System Technology），2009，33（18）：57-62.

[3]伍力，吴捷，钟丹虹（Wu Li，Wu Jie，Zhong Danhong）.多目标优化改进遗传算法在电网规划中的应用（Application of an improved genetic amgorithm in multi-objective power network optimization planning）[J].电力系统自动化 （Automation of Electric Power Systems），2000，24 （12）：45-48.

[4]何井龙，杨红梅（He Jinglong，Yang Hongmei）.基于合作协同进化和IMPSO算法的多阶段多目标电网规划（Multi-stage and multi-objective transmission planning based on IMPSO and cooperative coevolutionary algorithm）[J].电力系统保护与控制（Power System Protection and Control），2008，36（20）：10-14.

[5]王茜，张粒子，舒隽，等（Wang Qian，Zhang Lizi，Shu Jun，et al）.基于阈值选择策略的改进混合蛙跳算法在电网规划中的应用（Application of improved shuffled frog leaping algorithm based on threshold selection strategy in transmission network planning）[J].电力系统保护与控制（Power System Protection and Control），2011，39 （3）：34-39.

[6]Agarwal S K，Torre W V.Development of reliability targets for planning transmission facilities using probabilistic techniques-a utility approach[J].IEEE Trans on Power Systems，1997，12（2）：704-709.

[7]Gomez J F，Khodr H M，De Oliveira P M，et al．Ant colony system algorithm for the planning of primary distribution circuits[J]．IEEE Trans on Power Systems，2004，19（2）：996-1004．

[8]范利国，牛东晓（Fan Liguo，Niu Dongxiao）.基于区间层次分析法的输电网规划综合评价决策（An IAHP-based MADM method in transmission network planning）[J].电力系统保护与控制（Power System Protection and Control），2007，35（12）：47-51.

[9]符杨，孟令合，朱兰，等（Fu Yang，Meng Linghe，Zhu Lan，et al）.Pareto蚁群算法在多目标电网规划中的应用（Pareto ant colony algorithm for multi-objective power network planning）[J].电力系统及其自动化学报，（Proceedings of the CSU-EPSA）2009，21（4）：41-45．

[10]郭壮志，吴杰康（Guo Zhuangzhi，Wu Jiekang）．水电站厂内经济运行的快速仿电磁学算法（Study of fast electromagnetism-like mechanism on in-house economic operation of hydropower plant）[J]．现代电力（Modem Electric Power），2010，27（3）：89-94.

[11]王锡凡．电力系统优化规划 [M]．北京：水利电力出版社，1990．

[12]丁伟，胡兆光（Ding Wei，Hu Zhaoguang）.智能工程理论扩展及其在电网规划中的应用（Intelligent engineering theory expanding and its application in transmission planning）[J]．中国电机工程学报（Proceedings of the CSEE），2008，28（16）：15-21.

[13]程浩忠，高赐威，马则良，等（Cheng Haozhong，Gao Ciwei，Ma Zeliang，et al）．多目标电网规划的分层最优化方法（The lexicographically stratified method for multiobject optimal electric power network planning）[J]．中国电机工程学报（Proceedings of the CSEE），2003，23 （10）：11-16．

Application of Improved GAAA Hybrid Algorithm in Multi-objective Power Network Planning

KONG Xiang-cong，ZHOU Bu-xiang，RU Rui-rui，XIAO Xian，YE Zong-bin
（School of Electrical Engineering and Information，Sichuan University，Chengdu 610065，China）

To solve the multidimensional variables problems of multi-objective power network planning，the paper carries on the modelling from applying the GAAA hybrid algorithm in multi-objective power network planning.A multidimensional dynamic programming model is established to describe the economic efficiency，reliability，and N-1 static security of the power network.To improve the performance of the GAAA，the paper respectively makes better the follwing measures：population initialization，pheromone updating with elitist strategy，the variable discretization and cross-border processing，which can enhance the convergence and optimization efficiency of the GAAA.At last，the paper tests a 46-bus system and draws a conclusion，which shows that the improved algorithm can effectively solve the multi-dimensional combination problems with discrete variable optimization of power network planning.

multi-objective power network planning；global optimization；convergence；discrete variable；genetic algorithm and aolony algorithm（GAAA）

TM715

A

1003-8930（2013）06-0112-05

孔祥聪（1986—），男，硕士研究生，研究方向为电力系统自动化及计算机信息处理、分布式电源等。Email：843425610@qq.com

2013-03-26；

2013-05-08

周步祥（1965—），男，博士，教授，主要从事电力系统自动化、计算机应用等方面的研究工作。Email：hiway_scu@126. com

汝锐锐（1987—），男，硕士研究生，研究方向为电力系统自动化及计算机信息处理、分布式电源等。Email：349690848@qq.com