振动频率对饱和黏土动力特性的影响

郑 刚，霍海峰，雷华阳，张立明

(1. 天津大学滨海土木工程结构与安全教育部重点实验室，天津 300072；2. 天津大学建筑工程学院，天津 300072)

振动频率对饱和黏土动力特性的影响

郑 刚1,2，霍海峰1,2，雷华阳1,2，张立明1,2

(1. 天津大学滨海土木工程结构与安全教育部重点实验室，天津 300072；2. 天津大学建筑工程学院，天津 300072)

为了了解振动频率对饱和黏土动力特性的影响，针对天津临港工业区典型黏土做了一系列原状土与重塑土的动力试验．结果表明，随着频率的增加，原状土变形曲线由破坏型向发展型再向渐稳型过渡，重塑土变形曲线多为直线型．对4种动变形曲线定义了不同的破坏标准，发现随着振动频率的增加，软黏土动强度的变化趋势为先提高，之后增长幅度减小．频率越低，原状土的孔压升高越快；但振动频率对于重塑土孔压发展影响较小，原状土的界限孔压比低于重塑土．振动频率越低，原状土的动弹性模量软化指数下降得越快，并最终稳定在界限软化指数；不同振动频率下，重塑土软化指数的发展较为一致．

振动频率；动强度；动孔压；动弹性模量；软化指数

近年来，沿海城市兴建了大量的建筑物与构筑物，如高层建筑、高速公路、地铁隧道和港口码头等，在这些建筑物与构筑物建设过程与服役期间，土体受到动力循环荷载作用可能造成土体结构性破坏，动孔压的消散带来工后沉降，故其动力特性的变化规律成为人们关注的重点．为保证建筑物的安全稳定，研究黏土在动力荷载作用下的力学性状显得十分重要．

荷载的速率效应一直是研究者比较关注的课题，而在循环荷载中速率效应主要反映为振动频率的改变．不同频率动荷载作用下，土体的动变形、动强度有所不同，并直接影响到动参数的选择．人类的生产生活中存在着各种频率的动荷载，如：地震荷载频率较高；交通荷载的变化较大，其频率与交通工具选取及运行时间段有关，对于地铁，频率一般大于2,Hz；爆破荷载的频率相对比较高；波浪荷载一般小于1,Hz．考虑到不同类型荷载的特点，基于建设中滨海新区地质条件进行不同频率下黏土的动力特性研究，成为加快新区建设、科学合理地利用现有土地资源的重要研究课题．

关于振动频率对饱和黏土力学性状的研究，前人已取得了一些成果[1-3]，但并未得出比较一致的结论．Yasuhara等[1]认为，振动频率对于土体变形几乎没有影响；而张茹等[3]发现，在0.1～4.0,Hz范围内，动强度随频率的升高而增大，但频率继续升高后，动强度却有下降．笔者进行了动力三轴试验，分析了不同振动频率下土体的动力变化规律；着重探讨了振动频率对原状土、重塑土的动变形、动强度、动孔压以及动弹性模量的影响；在此基础上与重塑土进行对比分析，以加深对其动力特性的了解和认识．

1 试验土样与试验步骤

1.1 试验土样

所用土样取自天津临港工业区，深度10,m，地下水位较浅，土样呈灰褐色，中压缩性，可塑状态．具体物理指标如表1所示．

表1 原状土主要物理参数Tab.1 Major physical parameters of undisturbed clay

1.2 试验步骤

试验采用英国GDS动态三轴试验仪，试验中围压与反压精度控制在2,kPa以内，竖向动应力由电磁激振力施加，最大振动频率为5.0,Hz．试验步骤如下所述．

(1) 原状土制备：按规范要求将原状土切成直径39.1,mm、高80,mm的土样，切好的土样放入真空饱和器内抽真空2,h，达到需要的真空度后注入无气水，再抽2,h并静置10,h以上．饱和前可在土样周围裹上一层保鲜膜以防止土样因浸泡时间过长而变软．为确保饱和度达到98%，试验前将对土样进行B检测，若达不到要求，则反压饱和直至满足要求．

重塑土制备：原状土风干后捣碎并过0.5,mm筛，控制土样的干密度为1.5,g／cm3；取一定质量的干土粉，将干土粉分为等量3份，分3次在击实器内制备直径39.1,mm、高80,mm的重塑样．试样制好后同样裹一层保鲜膜并进行抽真空饱和，饱和方法同原状土．

(2) 试样在有效围压σ3，=100,kPa下进行等向固结，以孔压下降到等于反压为固结完成标准．

(3) 施加偏应力qs并马上进行循环剪切．动应力波形采用正弦波，振幅等于所施加偏应力，即σd= qs．在施加偏应力与动力剪切过程中，土样均为不排水状态，动应变、动孔压均为动应力在平衡位置所测．试验主应力变化如图1所示．

图1 动三轴试验主应力与时间关系Fig.1 Deviatoric stress in cyclic triaxial tests

定义动应力比r=σd/2,σ3，．对于原状土，试验在动应力比r=0.200和r=0.225下进行，振动频率分别为0.2,Hz、0.5,Hz、1.0,Hz、2.0,Hz、3.0,Hz和5.0,Hz；重塑土试样强度较低，高动应力比荷载作用下试样很快破坏，为更好表现出振动频率对其变形的影响，重塑土动应力比取较小值，分别为r=0.125，r=0.150，r=0.175，振动频率分别为0.2,Hz、0.5,Hz、0.7,Hz、1.0,Hz、2.0,Hz、3.0,Hz、5.0,Hz．

2 试验结果分析

2.1 动轴向应变

数据经处理发现，不同动应力比下，土体变形随振动频率的变化趋势较一致，故下面仅列出原状土r=0.225、重塑土r=0.150的试验结果．

图2为不同振动频率作用下轴向动应变随振动次数N变化的曲线．可以看出，随频率的增加，相同振次下土样的轴向累积变形减小．当频率为0.2,Hz时，原状土与重塑土的应变曲线均为破坏型，即初期应变增长缓慢，当轴向动应变达到某一临界值后，土样在较小振动次数下迅速增大，发生脆性破坏．

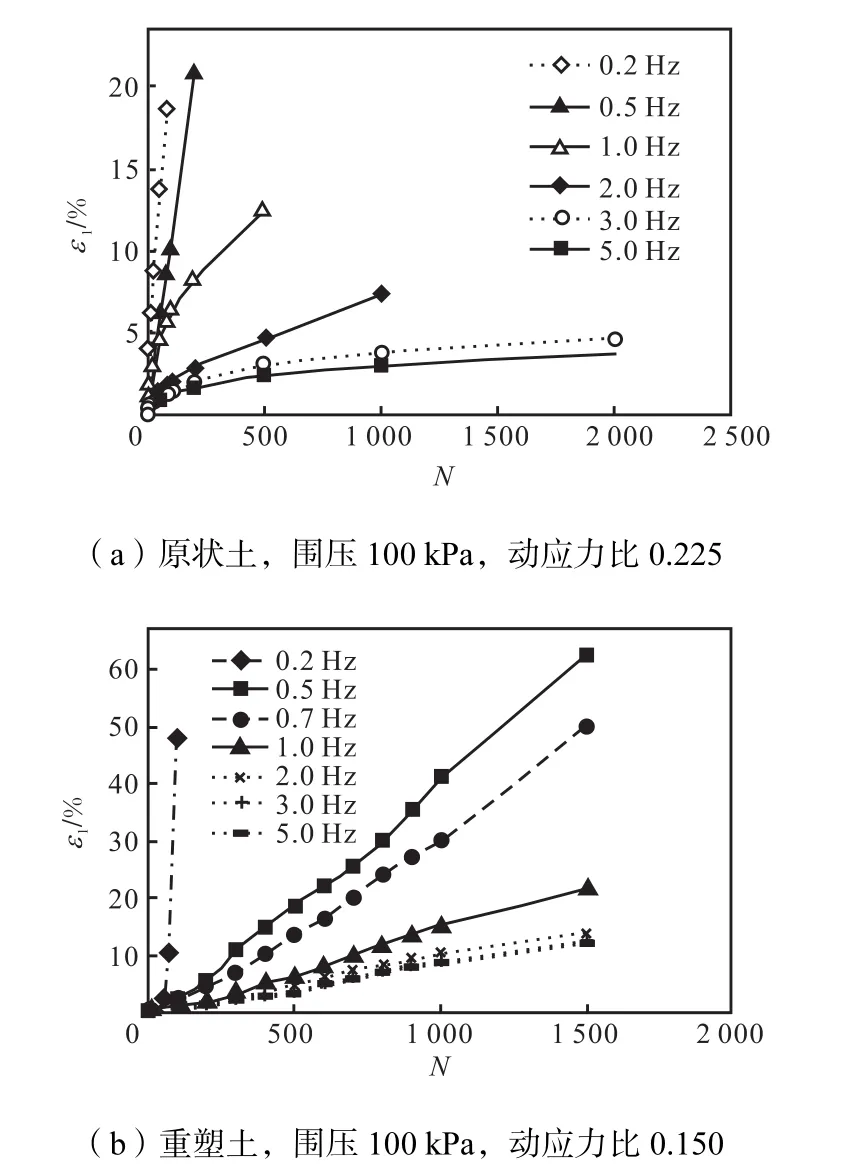
图2 不同振动频率下的轴向动应变发展曲线Fig.2 Axial dynamic strain curves of clay under different vibration frequencies

当振动频率大于0.5,Hz时，原状土应变曲线表现为发展型，即初始阶段轴向动应变增长较快，之后出现转折点，应变继续增加，但增长幅度减小；而重塑土轴向变形曲线则表现为直线型，轴向动应变近似随振动次数的增加而线性增加．

当振动频率大于3.0,Hz时，原状土应变曲线较为接近，振动初期，土样在较小循环振次下，变形增长较快，之后增长幅度减缓并有趋于稳定的趋势，笔者定义该种形式为渐稳型．重塑土的应变曲线则呈直线型，而且从图2(b)可以看出，在高频率下，重塑土样的轴向变形曲线较为接近，即振动频率由2.0,Hz提高为5.0,Hz时，轴向应变的变化远不如振动频率在0.2～1.0,Hz之间变化时引起的轴向应变的变化显著，其中振动频率由3.0,Hz提高为5.0,Hz时，二者对应的轴向应变几乎相同．

2.2 动强度

黏性土动强度的确定与选取的破坏标准有关，目前应用较多的的破坏标准主要有4种[4]．第1种为液化标准，即孔压达到围压使得有效压力为0；第2种为极限平衡标准，即土体的应力状态达到抗剪强度包线；第3种为双幅轴向动应变标准，通常取双幅动应变达到5%时破坏；对于黏性土，由于土颗粒具有黏滞作用，动孔压很难达到围压，双幅轴向动应变一般也低于5%，因此针对黏性土还提出了第4种标准，即累积轴向应变破坏标准．

对于第4种通过轴向累积变形曲线判定破坏的土样，陈颖平等[5]认为，循环荷载作用下，土样轴向变形曲线会出现转折点，转折出现后，很小的振次内动应变迅速增大，发生脆性破坏，可定义应变曲线达到转折点所需的振次为破坏振次．但并非所有动应变曲线均为破坏型，很多情况下应变不出现拐点而是随振次平稳发展或趋于稳定，这时可取一定的轴向动应变作为破坏标准．对于饱和黏性土，达到破坏标准的轴向动应变一般在2.5%～10.0%之间选取[6]，通常情况下破坏应变据建筑物的重要等级而定．

通过对本次试验结果的研究，笔者将循环荷载作用下土样轴向动应变的发展曲线分为4类，分别定义了破坏标准．如图3所示．第1类曲线为破坏型，此种曲线剪切初期应变发展缓慢，随后在较小振次下变形迅速增大，可取转折处为破坏振次．第2类为直线型，取达到一定轴向动应变的振次作为破坏振次．第3类为渐稳型，即变形发展到一定程度后变化较小，有稳定的趋势；此类曲线，如达到选定的轴向应变破坏标准应变值时，可认为此时发生破坏．第4类为发展型，初始阶段轴向动应变迅速增加，之后增幅放缓呈直线型．笔者认为，此两个应变发展阶段分别对应不同的土体内部结构，曲线转折处对应了土体原有结构发生破坏并向新结构转变的过渡，可取为破坏点．

图3 轴向动应变发展曲线Fig.3 Axial dynamic strain curves

图4 (a)为分别在破坏标准取允许轴向应变与本文定义的标准下，原状土破坏振次与振动频率的关系．由图2(a)可以看出，高频率下，轴向变形较小，为方便比较，允许轴向应变取2.0%．两种标准下破坏振次随频率变化曲线较为一致，当振动频率小于3,Hz时，随频率的增加，破坏振次增大；之后上升趋势放缓．图4(b)中重塑土表现出与原状土相似的性质，出现转折时的频率为2,Hz．这与潘林有等[7]的研究结果较为一致，即相比低频循环荷载，振动频率大于2,Hz时，动强度增加幅度会有所降低．

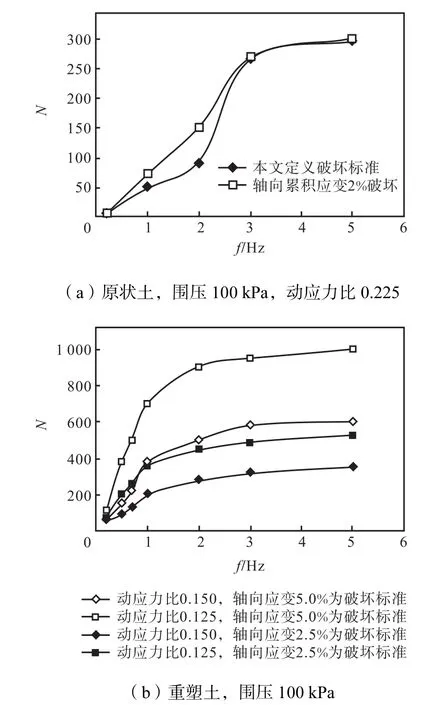
图4 破坏振次与频率关系曲线Fig.4 Curves of relationship between vibration time and vibration frequency

2.3 动孔压

对于饱和黏土，循环荷载作用下土样存在一个界限孔隙水压力ucr，即动孔压总会小于某一界定值，不大可能出现砂土的液化情形[8]．

图5(a)为原状土动孔压比ud/σ'3随振次发展曲线．可以看出，振动频率对于饱和软黏土孔压增长的影响较大．相同振动次数下，频率越大，产生的孔压越小．当频率小于0.5,Hz时，孔压增长很快，振次为200时，孔压比即达到了0.8；频率大于2.0,Hz时，孔压发展缓慢，孔压比在0.7左右达到稳定．

图5(b)为重塑土动孔压比随振次的发展曲线．可以看出，不同振动频率下的重塑土的动孔压发展曲线较为一致．初始阶段上升明显，之后增加趋势放缓，达到界限动孔压比后，孔压基本不再变化．重塑土的界限孔压比大概在0.9，高于原状土的界限孔压比(0.7～0.8)．

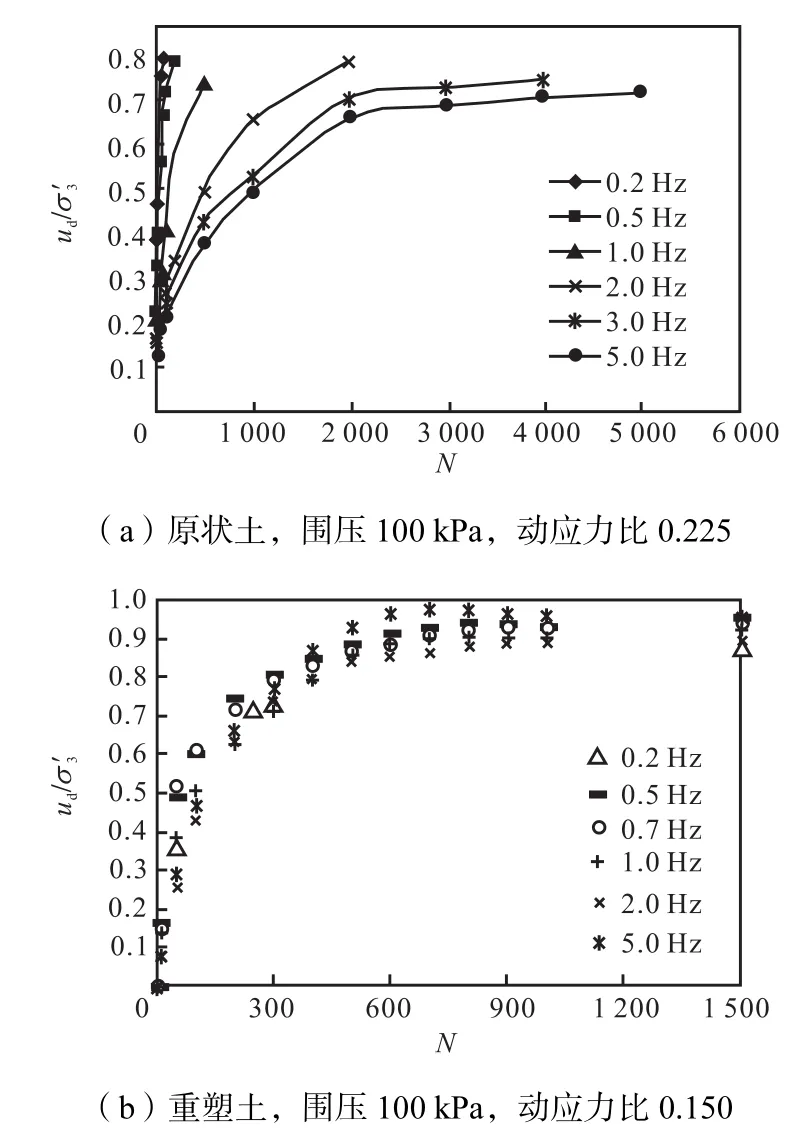
图5 不同频率下动孔压发展曲线Fig.5 Dynamic pore pressure curves of soft clay under different vibration frequencies

2.4 动弹性模量

饱和软黏土在循环荷载作用下，动弹性模量Ed将随着振动次数的增加有所降低，称为黏土的应变软化．本次试验采取等应力幅值控制加载，黏土在循环荷载作用下应力应变曲线具有滞后性，即每一次循环动应变极值较相应的动应力极值的出现会有所滞后．由于本文计算动弹性模量时取应力极值点，故计算值较真实值稍大，但对不同的试验结果进行比较时，其前提条件还是一致的．

根据Idriss等[9]提出的软化指数概念，定义动弹性模量软化指数δ为

式中Ed,1、Ed,N分别为第1次循环与第N次循环的动弹性模量．

图6(a)为不同振动频率下原状土动弹性模量随轴向应变的发展曲线．可以看出不同频率下，饱和软黏土的动弹性模量随应变的增加均有所下降，这与土样在受荷载作用下动孔压的产生以及结构性的破坏有关．较低频率下，动弹性模量初始阶段下降较快，随着动应变的增加，动弹模逐渐趋于稳定；较高频率下，土体轴向累积变形较小，动弹模迅速降低．由图6(a)可以看出，相同轴向应变下，动弹性模量随振动频率的增加而增大 ．

图6(b)为重塑土动弹性模量随轴向应变的发展曲线．可以看出，不同振动频率下，动弹性模量随轴向应变增大不断减小，表现出应变软化的性质．振动频率对于动弹性模量的影响不可忽略，当频率为0.2,Hz、0.5,Hz、0.7,Hz时，起初下降较快，之后下降幅度减缓，但是并不趋于稳定；当频率为2.0,Hz、3.0,Hz、5.0,Hz时，3条曲线几乎重合，且均表现为初始阶段动弹性模量衰减较快，当轴向应变大于5%后，Ed开始稳定，不再发生变化．在相同轴向应变的情况下，随着振动频率的增加，Ed不断增大．较为一致，界限指数大概在0.4左右，对应的变形曲线均为直线型．

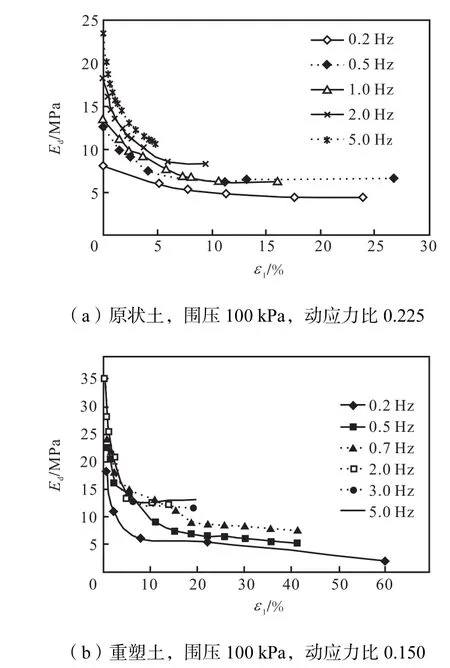
图6 不同频率下动弹性模量随轴向应变发展曲线Fig.6 Relationship between dynamic elastic modulus and axial strain under different vibration frequencies

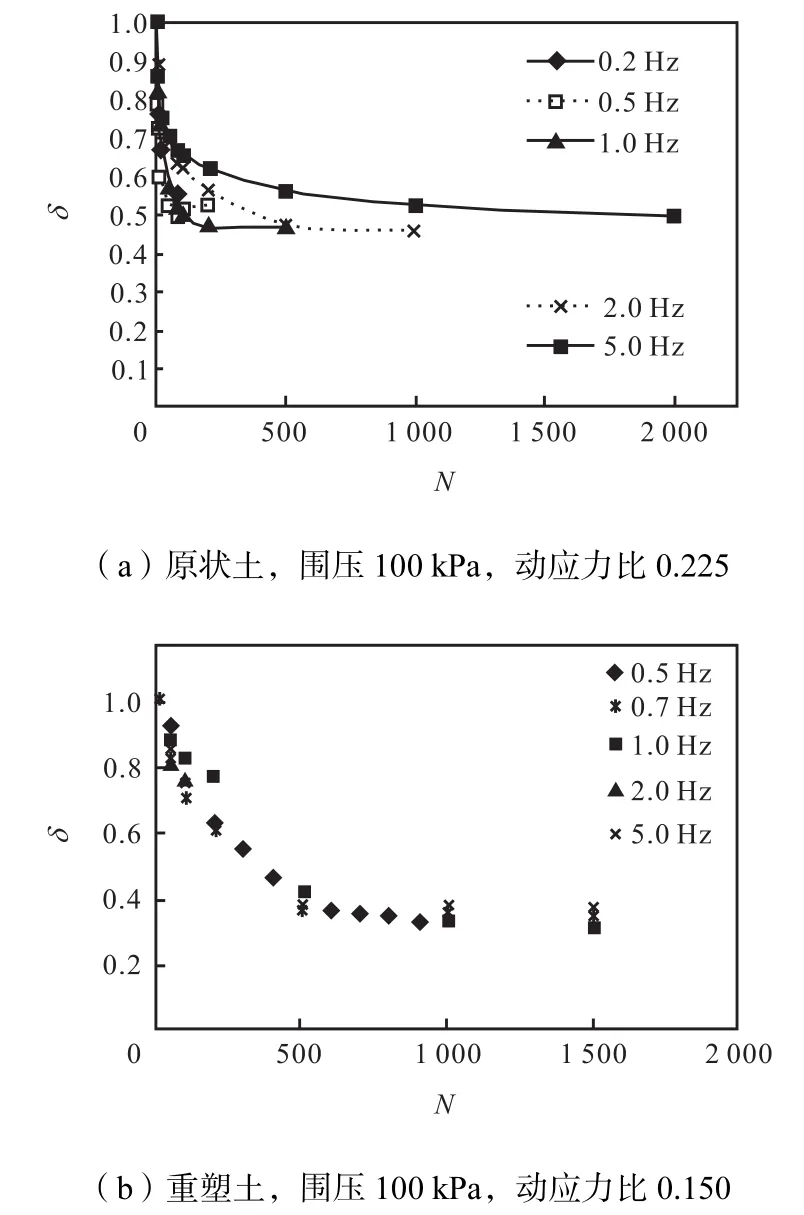
图7 动弹性模量软化指数发展曲线Fig.7 Softening ratio curves of dynamic elastic module

图7 (a)为原状土的动弹性模量软化指数发展曲线．可以看出，不同频率下软化指数曲线的发展模式较为一致；起初下降很快，之后经过过渡阶段稳定在0.5左右．说明在一定的初始状态下，软化指数存在一个界限值，达到界限值后软化指数不再减小，振动频率对于此界限值的确定没有影响．振动频率越低，软化指数下降得越快，达到稳定所需振次越少．

图7(b)为重塑土的动弹性模量软化指数发展曲线．可以看出频率大于0.5,Hz时，软化指数发展曲线

3 结 论

(1) 循环荷载作用下，原状土的轴向应变曲线随振动频率增加，由破坏型向发展型再向稳定型变化．较低振动频率循环荷载作用下，原状土与重塑土均有可能发生脆性破坏．当振动频率大于3.0,Hz时，频率对于土样变形的影响较小．

(2) 对4种动变形发展模式定义了不同的破坏标准，分别为破坏型曲线以转折点作为破坏标准，直线型与稳定型取允许达到的轴向应变值，发展型取转折点处．在此破坏标准下，当频率处于0.2～3.0,Hz之间时，饱和软黏土动强度随频率的增加而增大；频率在3.0～5.0,Hz之间时，动强度增长的幅度放缓．

(3) 相同振次下，原状软黏土的孔压随频率的增加而减小；而不同频率下，重塑土孔压发展较为相似．原状土界限孔压比低于重塑土．

(4) 振动频率越低，原状土的动弹性模量软化指数下降得越快，并最终稳定在界限软化指数；当变形曲线为直线型时，不同振动频率下，重塑土软化指数的发展较为一致．

参考文献：

［1］ Yasuhara Kazuya，Yamanouchi Toyotoshi，Hirao Kazutoshi. Cyclic strength and deformation of normally consolidated clay[J]. Soils and Foundations，1982，22(3)：77-79.

［2］ Hyde A F L，Yasuhara Kazuya，Hirao Kazutoshi. Stability criteria for marine clay under one-way cyclic loading[J]. Journal of Geotechnical Engineering，1993，119(11)：1771-1889.

［3］ 张 茹，涂扬举，费文平，等. 振动频率对饱和软黏土动力特性的影响[J]. 岩土力学，2006，27(5)：699-704. Zhang Ru，Tu Yangju，Fei Wenping，et al. Effect of vibration frequency on dynamic properties of saturated cohesive soil[J]. Rock and Soil Mechanics，2006，27(5)：699-704(in Chinese).

［4］ 赵 慧. 循环荷载作用下粉土的破坏标准及动力特性的试验研究[D]. 南京：河海大学岩土工程研究所，2006. Zhao Hui. Study on Tests of Failure Criterion and Dynamic Properties of Silt Under the Cyclic Loading[D]. Nanjing：Geotechnical Research Institute，Hohai University，2006(in Chinese).

［5］ 陈颖平，黄 博，陈云敏. 循环荷载作用下结构性软黏土的变形和强度特性[J]. 岩土工程学报，2005， 27(9)：1065-1071. Chen Yingping，Huang Bo，Chen Yunmin. Deformation and strength of structural soft clay under cyclic loading [J]. Journal of Geotechnical Engineering，2005，27(9)：1065-1071(in Chinese).

［6］ 朱思哲，刘 虔，包承纲，等. 三轴试验原理与应用技术[M]. 北京：中国电力出版社，2003. Zhu Sizhe，Liu Qian，Bao Chenggang，et al. Triaxial Test Principle and Application Technology[M]. Beijing：China Electric Power Press，2003(in Chinese).

［7］ 潘林有，王 军. 振动频率对饱和软黏土相关性能的影响[J]. 自然灾害学报，2007，16(6)：204-208. Pan Linyou，Wang Jun. Effect of vibration frequency on relevant behavior of saturated soft clay[J]. Journal of Natural Disasters，2007，16(6)：204-208(in Chinese).

［8］ 聂庆科，白 冰，胡建敏，等. 循环荷载作用下软土的孔压模式和强度特征[J]. 岩土力学，2007，28(增)：724-729. Nie Qingke，Bai Bing，Hu Jianmin，et al. The pore pressure model and undrained shear strength of soft clay under cyclic loading[J]. Rock and Soil Mechanics，2007，28(Suppl)：724-729(in Chinese).

［9］ Idriss I M，Dobry R，Singh R D. Nonlinear behavior of soft clays during cyclic loading[J]. Journal of Soil Mechanics and Foundation，1978，104(12)：1427-1447.

Contrastive Study on the Dynamic Characteristics of Saturated Clay in Different Vibration Frequencies

Zheng Gang1,2，Huo Haifeng1,2，Lei Huayang1,2，Zhang Liming1,2
(1. Key Laboratory of Coast Civil Structure Safety of Ministry of Education，Tianjin University，Tianjin 300072，China；2. School of Civil Engineering，Tianjin University，Tianjin 300072，China)

A few dynamic tests are carried out to study the influence on dynamic characteristics of the undisturbed and remolded clay in Lingang industrial area of Tianjin under different vibration frequencies. The test results show that，with the increasing of vibration frequency，the axial strain curves development mode of the undisturbed clays transforms from destructive mode to development-oriented mode，then to the stable one，and that most of the axial strain curves of remolded silty clay are lineal. Failure criteria are defined for four different axial strain curves as the following：as the frequency increases，dynamic strength of both undisturbed and remolded silty clay increases rapidly at the beginning，and then the increase slows down. The lower the frequency is，the more rapidly the pore pressure of undisturbed silty clay goes up，but the vibration frequency has little influence on pore pressure development of the remolded，and the pore pressure ratio limit of the undisturbed is lower than that of the remolded. The lower the frequency is，the faster the soften ratio of undisturbed silty clay goes down. No matter what the vibration frequency is，it will always stable at the softening ratio limit in the end. For the remolded silty clay，the softening ratio curves have a similar tendency under different vibration frequencies.

vibration frequency；dynamic strength；dynamic pore pressure；dynamic elastic modulus；softening ratio

TU443

A

0493-2137(2013)01-0038-06

2011-08-14；

2011-12-09.

国家重点基础研究发展计划(973计划)资助项目(2010CB732106)；国家自然科学基金资助项目(51078262)；天津大学自主创新基金资助项目(2010XJ-0101)．

郑 刚（1967— ），男，博士，教授．

郑 刚，zhenggang1967@163.com．