基于发动机轴系扭振抑制的扭弯减振器分析

舒歌群，谭琳琳，卫海桥，覃 文，朱天宇，刘丽娜，赵文龙

(1. 天津大学内燃机燃烧学国家重点实验室，天津 300072；2. 广西玉柴机器股份有限公司，玉林 537005)

基于发动机轴系扭振抑制的扭弯减振器分析

舒歌群1，谭琳琳1，卫海桥1，覃 文2，朱天宇1，刘丽娜1，赵文龙1

(1. 天津大学内燃机燃烧学国家重点实验室，天津 300072；2. 广西玉柴机器股份有限公司，玉林 537005)

扭弯复合减振器能同时抑制扭转振动和弯曲振动，降低发动机噪声．以发动机轴系扭转振幅最小化为目标，研究了扭弯复合减振器的设计方法，并分析扭振减振器或弯振减振器参数偏离对扭转振幅曲线的影响．分析表明：增大扭振减振器惯量比、降低弯振减振器惯量比，能减小扭转振幅曲线的共振峰值；弯振减振器阻尼比和刚度偏离最佳参数后，能增大曲线共振峰值，但影响程度很小；扭振减振器阻尼比和扭转刚度的偏离能显著增大峰值．

轴系振动；扭弯减振器；扭振抑制

一直以来，发动机轴系振动的研究主要以扭转振动为主，采用的减振方法很多[1-2]，比较常见的是在曲轴自由端安装一个扭振减振器，如硅油减振器、橡胶减振器．近年来也有人研究利用曲轴的飞轮端[3]或联轴器代替减振器进行扭转振动的抑制[4]，但还没达到普遍应用．

发动机轴系振动本身为纵弯扭三维方向，尽管弯曲振动对振动的影响较小，但研究表明，弯曲振动是诱发发动机噪声的主要激励源之一[5-8]．早在19世纪80年代，文献[5]通过实验发现，采用橡胶减振器抑制轴系弯曲振动的同时，还能明显降低发动机转速范围内的声压级，改善乘坐舒适性．

随着发动机的小型化、高功率化以及振动噪声相关法规的日益严格，单减振器已经不能满足人们对发动机振动噪声的要求，越来越多的学者开始进行多个减振器组合研究[9-11]．由扭振减振器与弯振减振器组合而成的扭弯复合减振器，能同时进行轴系的扭振与弯振的控制，改善发动机噪声辐射，因此在发动机减振降噪的研究中逐渐被广泛关注．

文献[12]通过实验研究了几种调频不同弯振共振频率的扭弯复合减振器对弯曲振动加速度及内部声压级的抑制，发现扭弯减振器可明显改善发动机的NVH特性；文献[13]通过实验研究了3种不同共振频率的扭弯减振器对轴系扭振特性的影响．

大量学者通过实验研究发现，扭弯减振器对轴系有着非常显著的减振降噪效果，但关于扭弯减振器参数探讨却鲜有报道．笔者以曲轴自由端安装并联型扭弯减振器[10]后的轴系扭振模型为研究对象，探讨扭弯减振器的最佳参数设计方法及参数偏离最佳参数时对发动机轴系扭振特性的影响．

1 模型建立

发动机轴系的扭转振动分析，常以轴系一阶扭转共振频率为研究对象，此时整个轴系当量简化成无阻尼单自由度系统[1]，当在曲轴自由端安装并联型扭弯复合减振器后，整个轴系可以简化成3自由度系统，如图1所示．

由D’Alombert原理，系统运动方程为

式中：I为转动惯量；K为扭转刚度；C为阻尼系数；M为干扰力矩振幅．

设方程的解为

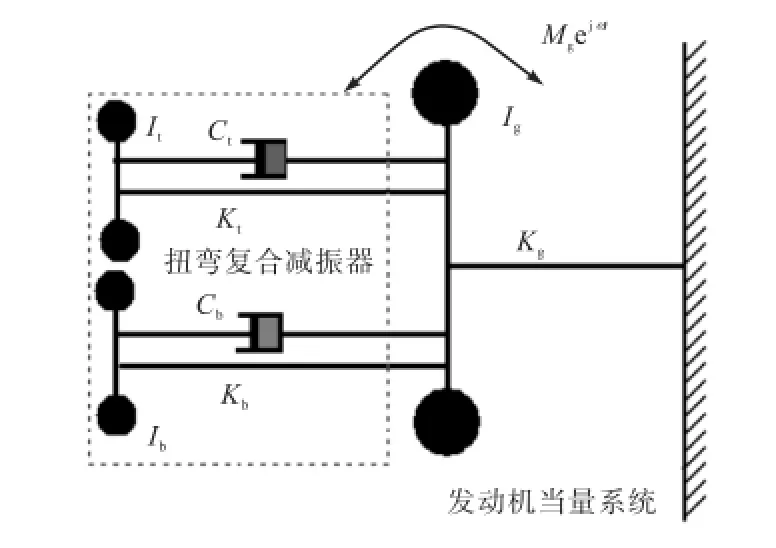
图1 轴系系统等效模型Fig.1 Equivalent model of crankshaft system

将式(2)带入式(1)得

求解矩阵方程(3)，可得

其中

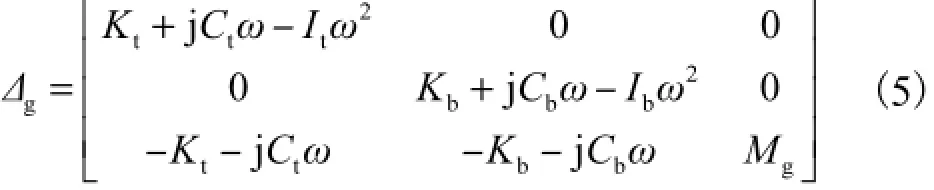
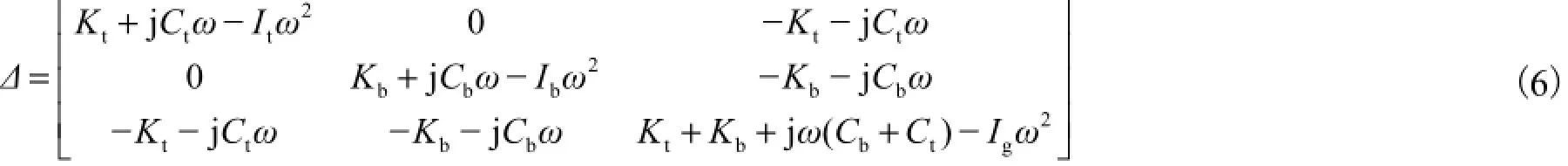
轴系扭转振幅放大因子为

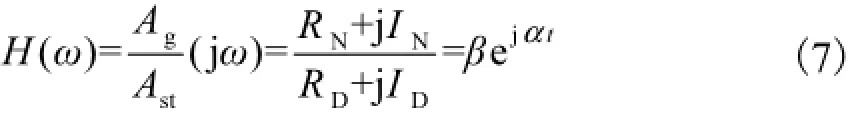
扭转振幅放大系数为

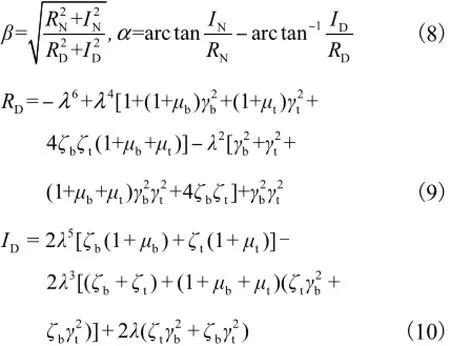
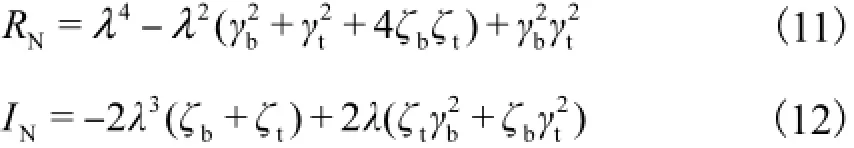
式中：下标g、b和t分别代表发动机当量轴系、弯振减振器、扭振减振器；Ast为轴系当量静振幅；Ag为轴系当量扭转振幅；ωn为轴系自振频率；ω为干扰力频率；λ为频率比；γb和γt分别为弯振减振器和扭振减振器减振器定调比；μb和μt分别为弯振减振器和扭振减振器惯量比；ζb和ζt分别为弯振减振器和扭振减振器阻尼比；

2 参数设计流程

通常研究中，曲轴系的扭振减振器主要为硅油减振器和橡胶减振器，弯振减振器则以橡胶减振器为主，因此图1所示的等效模型可代表轴系安装橡胶-橡胶型扭弯复合减振器．

由式(7)～式(12)可知，扭转振幅放大系数β 是扭、弯减振器的定调比、阻尼比与惯量比6个变量的综合函数．其中，弯振减振器主要调频弯曲振动，总体设计需要根据调频的弯振目标频率而定，因此其扭转振动特性参数有一定约束．假设在分析扭弯减振器对轴系扭振影响时，弯振减振器的固有频率为某一常数，其他参数可变．当弯振减振器定调比取不同常数时，随着扭振减振器定调比与频率比的变化，扭转振幅曲线变化如图2所示．

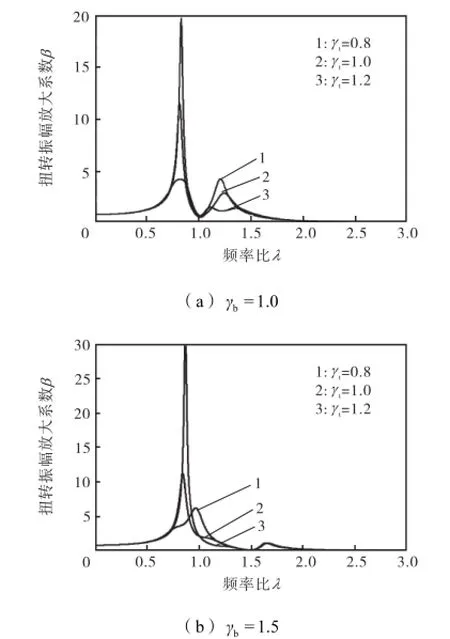
图2 扭弯减振器定调比γb、γt对放大系数β 的影响Fig.2 Influence of different values of γb,γton amplitudemagnification factor β

由图2可知，对于不同定调比组合的扭弯减振器来讲，扭转振幅放大系数曲线一般呈现3个共振峰．当tγ一定时，增大bγ，扭转振幅曲线的第3共振峰逐渐向坐标轴右侧移动，数值降低；当bγ一定且tγ小于1时，扭转振幅曲线的前2个共振峰比较显著，随着tγ的增大，第1共振峰值显著增大，第2和第3共振峰则逐渐降低并向高频方向移动；当bγ增大到1.5，第3共振峰相对于前2个共振峰来讲，数值过小，考虑扭弯减振器设计目标是降低最大共振峰值，因此，曲线的第3共振峰可以不用考虑．

对于发动机轴系来讲，通常危险的弯振共振频率要高于扭振共振频率，弯振减振器设计出来后的自身扭振固有频率通常也高于轴系扭振分析频率．因此当弯振减振器定调比大于1时，扭转振幅曲线将类似图2(b)．本文在求取扭弯复合减振器最佳参数时，仅研究前2个共振峰变化．

当其他参数不变时，在不同弯振减振器阻尼比情况下，改变扭振减振器的阻尼比，扭转振幅放大系数曲线变化如图3所示．

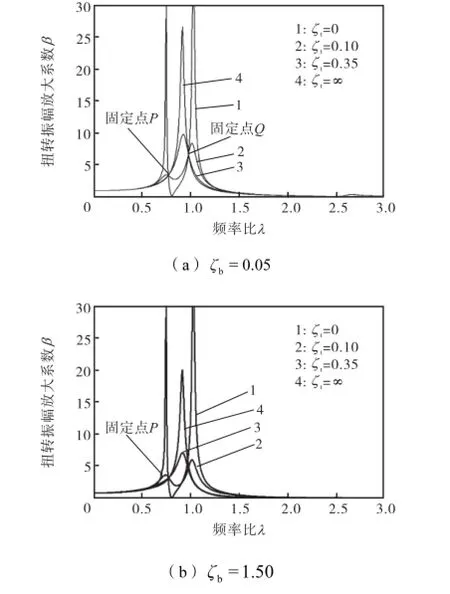
图3 扭弯减振器阻尼比ζb、ζt对放大系数β 的影响Fig.3 Influence of different values ofζb,ζton amplitudemagnification factor β

由图3可知，当bζ很小时，对于不同tζ，扭转振幅曲线始终过2个定点(见图3(a)中点P和点Q)；当bζ非常大时(见图3(b))，第1个固定点位置及振幅值保持不变，原第2个固定点的位置，振幅曲线虽然没经过同一点，但是聚集在该点附近的极小区域内，因此仍可近似认为经过同一固定点，同时发现此处的振幅数值明显比图3(a)中Q点小很多．也就是说，bζ只对第2固定点的振幅值有明显影响，对第1固定点振幅值无影响．

考虑阻尼的作用主要是降低共振处的振幅，而轴系弯振振幅本身很小，弯振减振器主要用来调节轴系弯振频率，对阻尼的要求很小，而实际橡胶弯振减振器的扭转阻尼系数也比较小，因此在进行以下分析时取橡胶减振器阻尼比bζ=0.05[1]．

从扭转振幅系数曲线始终经过2个固定点角度出发，扭弯复合减振器最佳参数求取的主要思路为：

(1) 已知弯振减振器定调比、扭弯减振器的惯量比时，求取使得图3(a)中固定点P和Q振幅相等的最佳扭振减振器定调比tγ；

(2) 改变扭振减振器阻尼比tζ，使得振幅放大系数曲线2共振峰值分别到2固定点P和Q的距离最小，并使得2个共振峰处于同一水平线上．上述步骤的流程如图4所示．

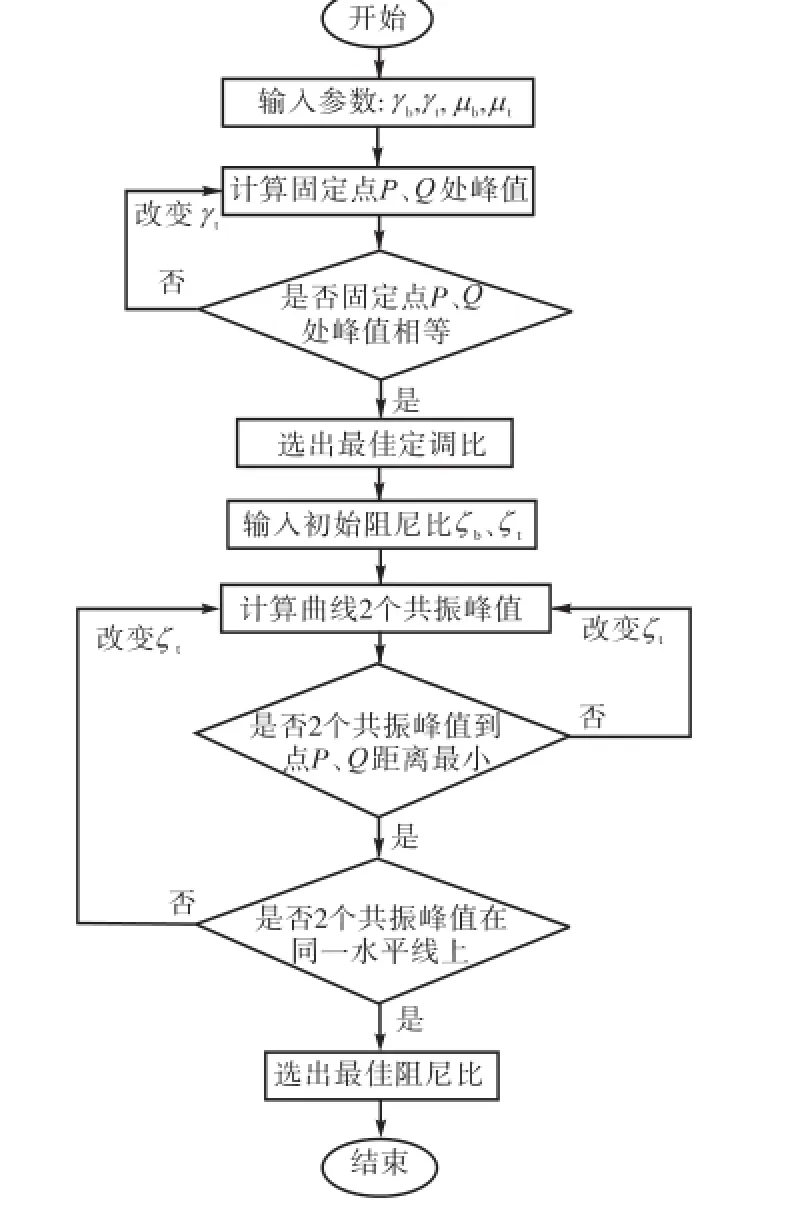
图4 最佳参数计算流程Fig.4 Optimal parameters calculation flowchart

3 算例及结果分析

3.1 扭弯减振器最佳参数设计

[7-8，13]，弯振减振器的扭振自振频率与轴系扭振目标频率之比在2.5～4，由于弯振减振器的扭振频率越高，其对轴系扭转振动的影响越不好，所以拟采用弯振与扭振频率比为2.5，即复合减振器中的弯振减振器定调比取2.5，按照图4的流程，采用Matlab软件编程，进行最佳参数计算[14]．当扭弯减振器惯量比均在0.05～0.21范围内变化时，扭转振幅的共振峰值、扭振减振器的最佳定调比和阻尼比变化情况分别如图5～图7所示．

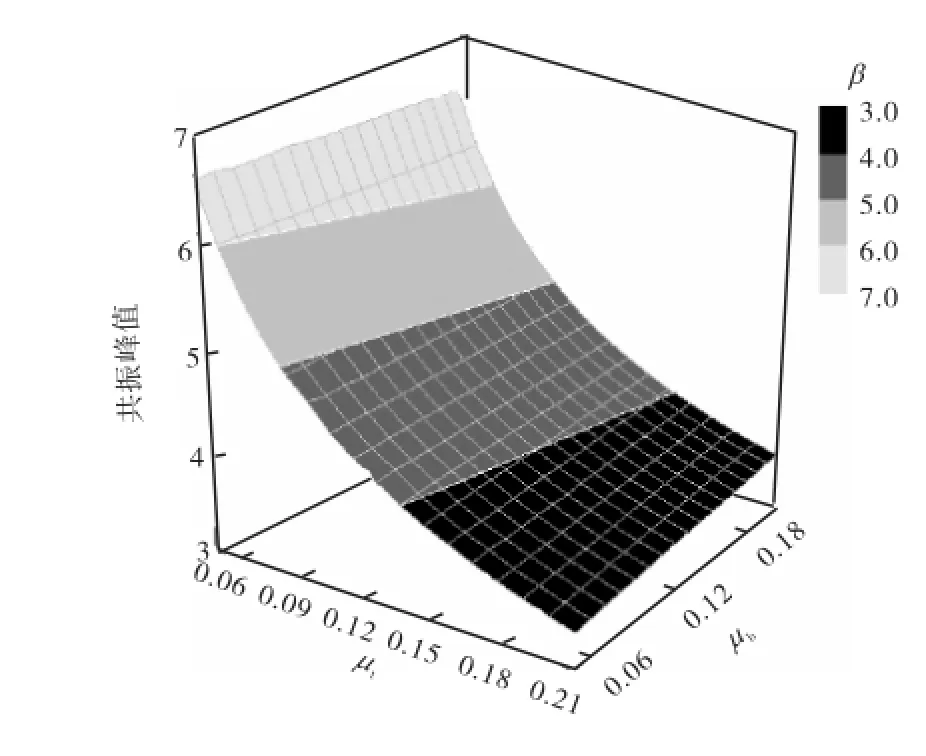
图5 扭弯减振器惯量比μb、μt对放大系数β 的影响Fig.5Influence of different values of μb,μton amplitude magnification factor β

3.1.1 扭振共振峰值

由图5可知，当弯振减振器惯量比bµ不变时，随着扭振减振器惯量比tμ的增大，共振峰值显著降低；当tμ不变时，bµ的增大使得共振峰值缓慢增大．因此可以推测，由于弯曲定调比比1大很多，增加弯振减振器的惯量将削弱扭振减振器对轴系扭转振动的抑制[15]．

3.1.2 扭振减振器最佳定调比

由图6可知，随着扭弯减振器惯量比tμ、bμ的增大，扭振减振器最佳定调比均呈现降低趋势，而tμ的变化对最佳定调比的影响则更大．因此可以推断，由于弯曲定调比比1大很多，弯振减振器的加入削弱了弯振减振器惯量比对扭转定调比的影响．

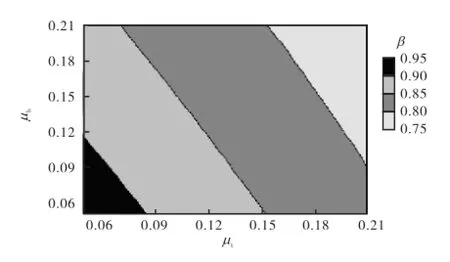
图6 扭振减振器最佳定调比γt与惯量比μb、μt的关系Fig.6 Relationship between optimalγtand μb,μt

3.1.3 扭振减振器最佳阻尼比

由图7可知，当弯振减振器惯量比bµ不变时，增加tμ，最佳阻尼比的取值呈缓慢增大趋势；当tμ不变时，增加bµ将使扭振减振器最佳阻尼比系数降低．

综合图5～图7可知，弯振减振器的加入，将使得扭振的共振峰值略有增大，但是扭振减振器的最佳定调比和阻尼比的取值则略有变小．

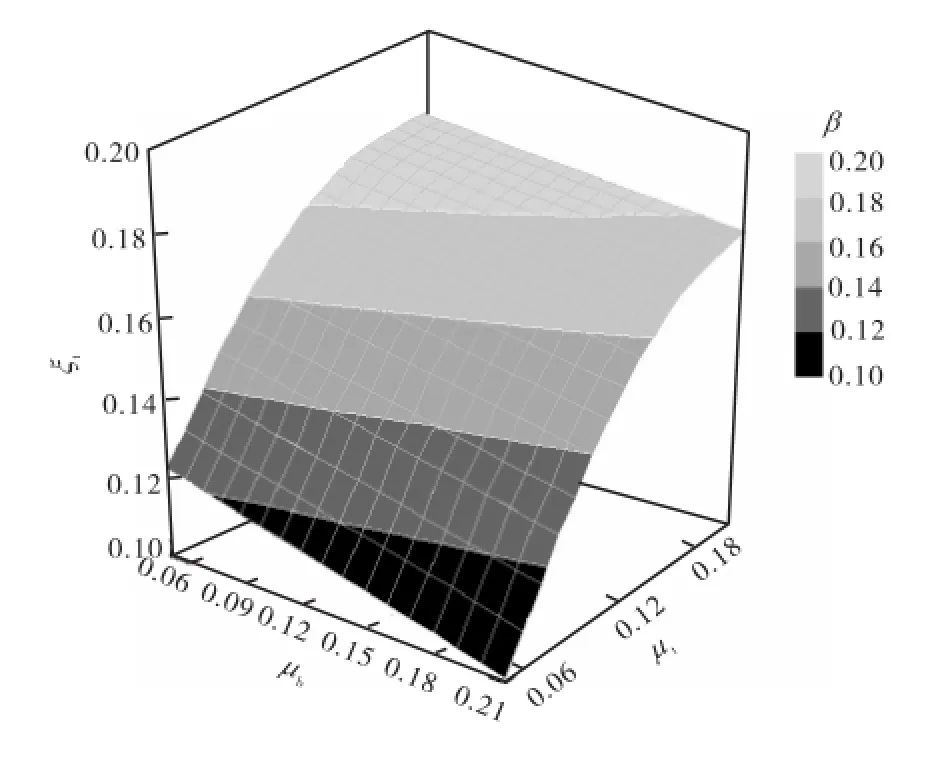
图7 扭振减振器最佳阻尼比ζt与惯量比μb、μt的关系Fig.7 Relationship between optimalζtandμb,μt

3.2 参数偏离最佳时对扭振特性的影响

3.2.1 扭转刚度的影响

当扭弯减振器按照最佳参数设计出来后，由于实际材料限制或随着实际的使用，复合减振器的刚度、阻尼等参数将会与最佳参数有一定的偏离，而使扭转振幅曲线不再有相等的共振峰．

当扭转刚度发生变化时，根据定调比表达式及式(1)～式(6)，可以得出新的扭转振幅放大系数曲线，其变化情况如图8所示．

由图8可知，当扭弯减振器按照最佳参数设计后，如果扭振减振器刚度发生变化，振幅曲线将发生显著的变化，原先的2个相等的共振峰也不再相等，呈现一增一减的趋势；当弯振减振器的刚度发生变化时，尽管2个共振峰也不再相等，但偏离数值较小，尤其当刚度比预设的刚度大时，其影响程度要比小于预设刚度的影响小．

3.2.2 阻尼比的影响

由图9可知，扭振减振器阻尼比tζ的变化能明显改变扭振振幅曲线的趋势，tζ偏离最佳参数会使共振峰数值增大，其趋势如图9(a)所示．改变同等数值时，阻尼比偏大要比偏小对于共振峰的影响更小.由图9(b)可知，当弯振减振器阻尼比bζ偏离预设值时，bζ的改变会使2个共振峰值不再相等，但曲线共振峰值几乎没变．

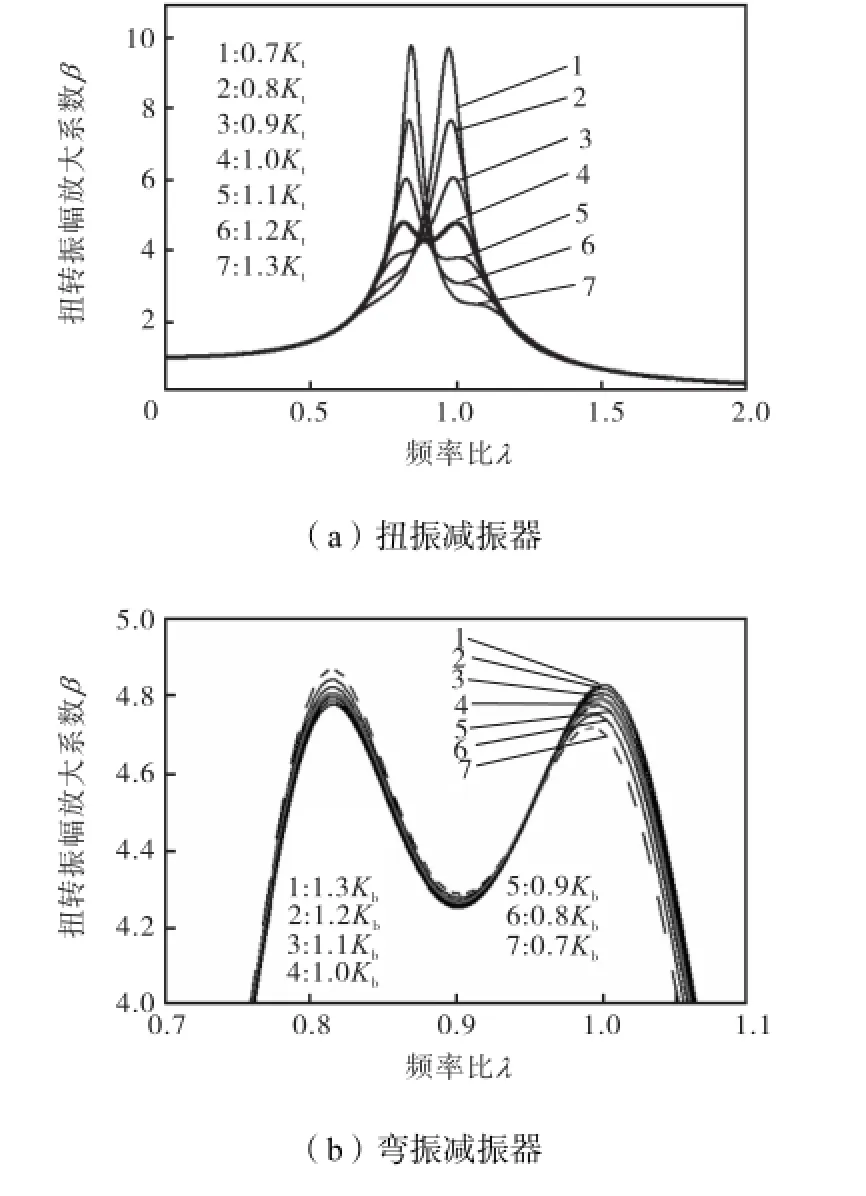
图8 扭弯减振器刚度Kt、Kb对放大系数β 的影响Fig.8Influence of tosional-bending damper’s stiffness Ktand Kbon amplitude magniication factor β

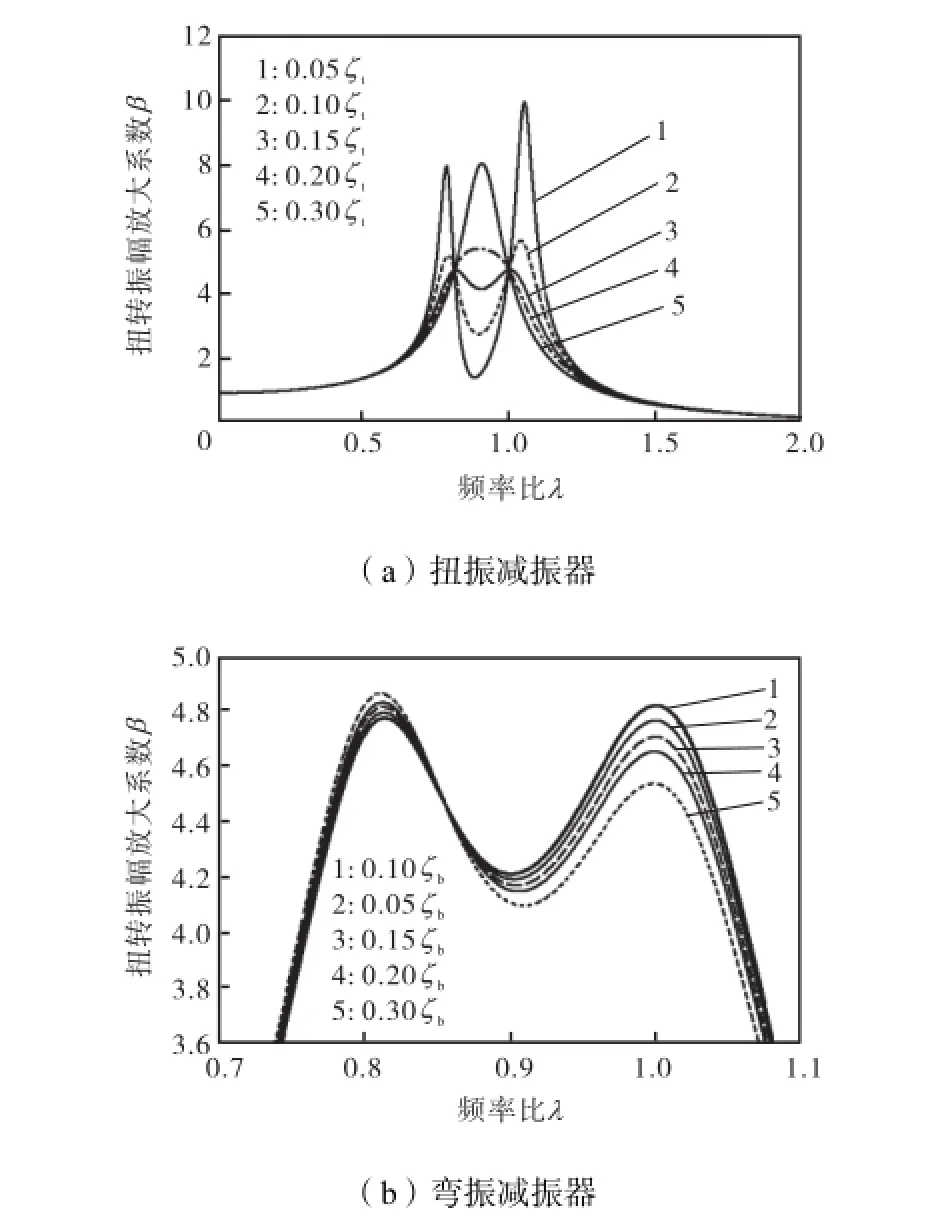
图9 扭弯减振器阻尼比ζt、ζb对放大系数β 的影响Fig.9Influence of tosional-bending damper’s damping ζt, ζbon amplitude magnification factor β

综合以上分析，当扭弯减振器中的阻尼比和刚度发生变化时，对共振峰的影响变化率δ(式(13))如表1所示．

式中：G为改变某一参数时的共振峰值；Gopt为最佳参数下共振峰值．

表1 扭弯减振器参数对共振峰的影响Tab.1 Influence of parameters of torsional-bending damper on resonance peak

从表1可知：当弯振减振器定调比确定且其扭转振动参数偏离最佳参数时，无论是阻尼比还是扭转刚度的改变均使共振峰值增大，扭转振动的抑制效果减弱，但参数偏离造成的影响非常小(上述分析中最大值为1.27%)，且弯振减振器参数高于设计的最佳参数，要比低于最佳参数对共振峰值的影响要小，因此实际二者的选取可适当增大范围；当扭振减振器的参数偏离最佳参数时，阻尼比及扭转刚度参数的增大或减小均显著影响共振峰值，使得共振峰值增大，恶化了扭振的抑制效果．因此实际2个参数的选取比较严格．

4 结 论

(1) 由于扭弯减振器的弯振减振器固有频率比轴系研究的扭振一阶固有频率高，因此带有扭弯减振器的扭转振幅放大系数曲线的前2个共振峰值比较显著，是进行轴系扭振抑制的主要研究对象．

(2) 弯振减振器阻尼比影响扭转振幅放大系数曲线第2处共振峰，对第1处共振峰无影响，在最佳参数求取中可以当成定值．

(3) 在求取扭弯减振器最佳参数时，对于不同的扭弯减振器惯量比，增大扭振减振器的惯量比，会使振幅系数曲线的共振峰值降低、扭振减振器的最佳定调比降低，但扭振减振器的最佳阻尼比升高；而增大弯振减振器惯量比会使上述3者呈相反趋势变化．

(4) 当实际参数偏离预设值时，弯振减振器的阻尼比和扭转刚度的偏离，对扭转振幅放大系数曲线的影响比较小，因此选取范围可适当放宽．扭振减振器的阻尼比和扭转刚度的偏离，明显增大振幅曲线的共振峰值，因此二者选取范围需要严格限制．

参考文献：

［1］ 汪长民，杨继贤，孙业保，等. 车辆发动机动力学[M]. 北京：国防工业出版社，1983. Wang Changmin，Yang Jixian，Sun Yebao，et al. Dynamics of Vehicle Engine [M]. Beijing：China National Defense Industry Press，1983(in Chinese).

［2］ Londhe A，Yadav V H. Design and optimization of crankshaft torsional vibration damper for a 4-cylinder 4-stroke engine[C]// SAE Paper. Detroit，Michigan，USA，2008，2008-01-1213.

［3］ Hu Jianjun，Qin Datong，Zhao Yusheng，et al. study on natural torsional vibration characteristics of dual mass flywheel-radial spring type torsional vibration damper [C]// SAE Paper. Detroit，Michigan，USA，2009，2009-01-2062.

［4］ 苏 芳，马建敏，刘 颖. 柔性联轴器对振动系统响应的影响[J]．噪声与振动控制，2012(1)：163-166.

Su Fang，Ma Jianmin，Liu Ying. Effect of flexible couplings on response of a vibration system[J]. Noise and Vibration Control，2012(1)：163-166(in Chinese).

［5］ Tamotsu K，Tomiaki A，Kazuyoshi T. Toyota’s new tope of crankshaft pulley to improve the compartment tone quality[C]// SAE Paper. Detroit，Michigan，USA，1988，880078.

［6］ 舒歌群，梁兴雨. 曲轴三维振动与机体裙部表面振动的耦合关系研究[J]. 农业工程学报，2006，22(1)：1-5.

Shu Gequn，Liang Xingyu. Coupling relationship between three-dimensional vibration of the crankshaft and surface vibration of the crankcase[J]. Transactions of the CSAE，2006，22(1)：1-5(in Chinese).

［7］ Klnoshlta M，Sakanoto T，Okamura H. An experimen-tal study of a torsonal/bending damper pulley for an engine crankshaft[C]// SAE Paper. Detroit，Michigan，USA，1989，891127.

［8］ Naganuma T，Okamura H，Sogabe K. Experiments and analyses of the three-dimensional vibrations of the crankshaft and torsional damper in a four-cylinder in-line high speed engine[C]// SAE Paper. Detroit，Michigan，USA，1997，971196.

［9］ Iwanami K，Seto K. An optimum design method for the dual dynamic damper and its effectiveness[J]. Bulletin of JSME，1984，27(131)：1965-1973.

［10］ Shangguan Wenbin. Multi-mode and rubber-damped torsional vibration absorbers for engine crankshaft systems[C]// SAE Paper. Detroit，Michigan，USA，2007，2007-01-2292.

［11］ 王红云，蔡锐彬，上官文斌. 发动机曲轴二级并联橡胶扭转减振器优化设计[J]. 车用发动机，2007(5)：52-55.

Wang Hongyun，Cai Ruibin，Shangguan Wenbin. The optimum design of the two staged parallel rubber torsional damper for engine crankshaft[J]. Vehicle Engine，2007(5)：52-55(in Chinese).

［12］ Sinan Lacin，Edson Lopes，Bilal Bazzi. An experimental(in-vehicle)study of a dual modec rankshaft damper for an engine crankshaft[C]// SAE Paper. Detroit，Michigan，USA，2003，2003-01-1676.

［13］ 舒歌群. 弯曲振动减振器对扭-弯减振器扭振减振性能的影响研究[J]. 内燃机学报，1998，16(3)：348-353.

Shu Gequn. Effect of bending vibration damper on properties of torsional vibration reduction for torsionalbending famper pulley[J]. Transactions of CSICE，1998，16(3)：348-353(in Chinese).

［14］ 徐进友，刘建平，宋轶民，等. 考虑电磁激励的水轮发电机组扭转振动分析[J]. 天津大学学报，2008，41(12)：1411-1416.

Xu Jinyou，Liu Jianping，Song Yimin，et al. Torsional vibation analysis of hydrogenerators considering electromagnetic excitation[J]. Journal of Tianjin University，2008，41(12)：1411-1416(in Chinese).

［15］ 杨志安，李文兰，邱家俊. 发电组轴系电磁激发横扭耦合振动[J]. 天津大学学报，2008，41(5)：583-588.

Yang Zhi′an，Li Wenlan，Qiu Jiajun. Lateral and torsional coupling vibration excited by electromagnetism of turbogenerator set rotor system[J]. Journal of Tianjin University，2008，41(5)：583-588(in Chinese).

Analysis on Torsional-Bending Damper for Engine Crankshaft Based on Torsional Vibration Reduction

Shu Gequn1，Tan Linlin1，Wei Haiqiao1，Tan Wen2，Zhu Tianyu1，Liu Lina1，Zhao Wenlong1
(1. State Key Laboratory of Engines，Tianjin University，Tianjin 300072，China；2. Guangxi Yuchai Machinery Company Limited，Yulin 537005，China)

The torsional-bending damper，including a torsional damper and a bending damper，plays an important role in restraining torsional and bending vibration of the crankshaft so as to lower noise. Aiming at minimizing the torsional amplitude，the method to design the torsional-bending damper was investigated，and the influence of the parameters’ deviation on the torsional amplitude was analyzed. Calculation results show that increasing the torsional damper’s interia ratio and decreasing the bending damper’s interia ratio would reduce the maximum peak of the torsional amplitude magnification curve；the deviation of parameters of bending damper’s damping ratio and stiffness can increase the resonant peak value at a small degree，the deviation of the torsional damper’s damping ratio and stiffness，however，would increase the peak value significantly.

crankshaft vibration；torsional-bending damper；restraining torsional amplitude

TK402

A

0493-2137(2013)11-0951-07

DOI 10.11784/tdxb20131101

2012-05-23；

2012-06-27.

国家高技术研究发展计划(863计划)资助项目(2012AA111702).

舒歌群（1964— ），男，博士，教授，sgq@tju.edu.cn.

覃 文，tanwen_2012@163.com．