基于广义逆非负矩阵分解的无线传感器网络节能通信
2013-06-04仵博1吴敏1
仵博1, 2, 3,吴敏1, 2
(1.中南大学 信息科学与工程学院,湖南 长沙 410083;2. 先进控制与智能自动化湖南省工程实验室,湖南 长沙,410083;3. 深圳职业技术学院 教育技术与信息中心,广东 深圳,518055)
无线传感器网络(WSN)是由随机分布的集成有传感器、数据处理单元和通信单元的微小节点通过自组织方式构成的无线网络。WSN具有廉价性、自组织性、动态性和高容错性等优点,在军事领域、医疗保健、环境监控和减灾救灾等领域得到广泛应用[1]。WSN传感器节点能量通常由电池供给,且难以及时补充。因此,如何高效使用能量来最大化网络生命周期是传感器网络面临的重大挑战[2]。WSN能量消耗主要用于传感器感知、通信和数据处理。研究表明:传感器节点的能量消耗主要集中在通信上,传感器结点通信所消耗的能量占整个传感器生命周期内能量的 80%以上。因此,有效降低传感器节点通信能量消耗是最大化 WSN生命周期的关键。通信能耗主要发生在传感器接收、发送和空闲3种状态下,通信能耗降低方法主要3类。一类是对WSN通信协议的改进来降低通信能耗[3-5],延长WSN的生命周期。但是,该类算法缺乏泛化能力,局限于特定的应用。一类算法是根据传感器所处环境的特征,采用部分可观察马尔可夫决策过程(POMDP)建模能量消耗与服务质量[6-7],从而实现能耗与网络性能的优化平衡。但是,该算法针对POMDP近似最优值求解存在“维数灾”问题,只能针对小规模 WSN系统,在大规模或者连续状态下,算法无法实现实时收敛。一类算法通过是压缩原始高维通信数据空间到低维空间,从而实现降低传输能耗的目的[8-9],该类算法具有模型无关性,泛化能力较强。但是,现有算法降维过程复杂,实时性不高。针对目前算法的优缺点,本文提出一种基于广义逆非负矩阵分解(giNMF)的无线传感器网络能量高效通信算法。在采用非负矩阵分解(NMF)降维之前,先采用广义逆分解技术(本文采用奇异值分解(SVD))对原始通信数据矩阵进行初始化操作,从而避免 NMF随机初始化带来的矩阵分解不确定性问题,然后,采用 NMF对奇异值分解后的特征空间进行降维。
1 非负矩阵分解
在实际的应用环境中,传感器传输的信息往往具有高维稀疏性,传输这些高维稀疏信息消耗大量的传感器能量。从认知心理学的理论可知,大脑对外界只会处理其中的“有意义”数据,而对其他数据“视而不见”,即高维信息空间往往可以由低维空间来本质表示。因此,建立传感器的高维数据到低维“有意义”数据的映射,传感器仅传输降维后的数据,将会大大降低通信能耗。
非负矩阵分解方法[10]是将原高维矩阵分解成为 2个低维非负矩阵的积,其原理如图1所示。

图1 非负矩阵分解原理示意图Fig. 1 diagram of nonnegative matrix factorization
给定一个m×n的矩阵 X = [ xi,j]m×n∈Rm×n代表m个变量n个特征值。NMF的目标是找到2个非负矩阵和最小化目标函数Ω。Ω是D(U||V)的损失函数,D为Kullback-Leibler(KL)散度,r<<m,r<<n,U>0,V>0。

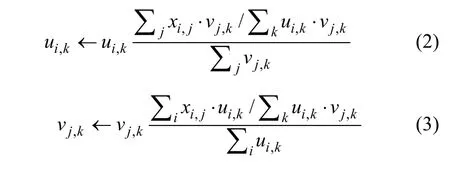
其中: Y = [ y ]= U · VT,如果X=Y,D(U||V)为0。i, j由于 U和 V 2个矩阵有且仅只有一个具有凸特性,因此,很难设计一个使目标函数全局最小的算法。Lee和Seung[10]证明利用式(2)和(3)可以使目标函数局部最小。
非负矩阵分解是处理高维数据集的重要方法,并在模式识别、信号处理、数据聚类和计算机安全等方面得到应用[11]。但是,非负矩阵分解还有一些缺点:(1) 对于大规模数据,计算NMF十分耗时,造成它无法在实时系统中应用[12];(2) 特征空间 r的维数无法预测,因此寻找一个最优的 r比较困难;(3) 无法求解全局最优,分解因子U和V的初始化是随机的,造成每次分解的结果不确定。
2 广义逆非负矩阵分解的通信数据压缩算法
基于非负矩阵分解存在的问题,利用广义逆的快速转换特性[11,13],提出一种基于广义逆非负矩阵分解算法,并将该算法应用于无线传感器网络传输信息压缩,实现能量高效通信。
2.1 广义逆矩阵构建
定义1[13]对于有限维矩阵X,Penrose定义存在一个唯一的广义逆矩阵†X 同时满足:

其中:X*为X的共轭转置矩阵。
定义2[13]令X∈Rm×n,存在2个正交矩阵U∈Rm×n和 V∈Rm×n,奇异值分解如下:

其中:Σ∈ Rm×n为对角矩阵:


2.2 特征空间变换
根据NMF分解原理可知, Xm×n= Um×r·Vr×n,其中,U为权重矩阵,V为基矩阵,特征空间变换过程为式(11)~(13)。

将式(11)两边同时乘以V的广义逆矩阵†V :

如果V的每行都是线性独立的,则,†≈VVI,I为单位矩阵,式(12)可变换为:

通过以上变换步骤,可以很快地将原始输入矩阵变换为权重特征空间。
2.3 广义逆非负矩阵分解的通信数据压缩算法
算法思想:首先对通信数据矩阵X进行广义逆分解,初始化X,快速得到X的特征空间,然后,根据误差约束条件或者时间约束条件,对广义逆分解后的X进行 NMF降维,从而实现对原始通信数据的有效快速降维。
定义3 在KL散度函数中,需要评估X和UV之间的误差,假设每步迭代导致一个ε误差,这个误差增加X和UV之间的距离,那么积累到步n时的误差为:

算法 1:广义逆非负矩阵分解的通信数据压缩算法(giNMF)
输入:原始通信数据矩阵X ∈ Rm×n
输出:U∈Rm×n和V ∈ Rm×n
// 奇异值分解操作
Step 1:采用广义逆奇异值分解方法,将X进行分解;
step 2:取X的前r个较大的奇异值σi及其对应的特征空间ui;
// NMF降维操作

Step 5:当误差约束条件或者时间约束条件满足时,算法终止;否则,循环执行Step 3和Step 4;
Step 6:输出降维后的U和V。
由于在NMF降维算法中,分解因子U和V的初始化是随机的,造成每次分解的结果不确定,有时甚至得到不正确或者不相关的分解结果。NMF算法的时间复杂度为 O(MNr),空间复杂度为 O(MN)。giNMF算法采用广义逆分解(算法Step 1和Step 2),很快得到原始矩阵的特征空间,避免迭代求解分解因子操作。Step 3和Step 4计算极小值的U和V直到循环条件满足,这2步是NMF降维算法,由于经过广义逆分解,所以 NMF降维的规模大大降低,采用乘法更新法则可以很快求解出最终的降维结果。giNMF算法的时间复杂度为O(Nr2),空间复杂度为O(Nr)。
算法giNMF具有通信模式无关性,无论是单跳还是多跳,对giNMF算法并无影响。因此,giNMF算法对通信数据降维具有较强的泛化能力,可以应用到任何模式、任何节点的通信数据传输中。
3 仿真实验
本文的实验对象为传感器采集、发送和接收环境温湿度的信息,传感器采用Crossbow MICA2 Mote,拓扑结构为单跳模式。为降低能耗,传感器往往采用采集多条信息集中发送方式,工作原理如图2所示。

图2 数据压缩工作原理Fig. 2 Operating principle of data compression
传输N个M位长的包,通信总能耗为数据采集阶段能耗、数据压缩阶段能耗、数据发送阶段能耗与数据接收阶段能耗之和。

根据文献[14]可知,数据采集阶段能耗Ea和数据压缩阶段能耗Ec远远小于发送和接收能耗,因此,在本文忽略 Ea和 Ec,只考虑 Es和 Er。根据文献[15],Es和Er计算如下:

其中,d为结点传感器与簇首传感器之间的距离。
本文分别从 3个角度进行实验分析:(1) 与文献[12]的lraNMF算法进行对比分析,比较giNMF算法的降维效果和耗时;(2) giNMF算法与LEACH算法的通信能耗对比分析;(3) giNMF算法与LEACH算法的网络生命周期的对比分析。
3.1 降维效果分析
降维效果比较如图3所示。根据图3可见:本文giNMF降维算法比 lraNMF降维算法具有较高的效率,针对KL散度的收敛速度,giNMF算法更快。对于相同的KL散度,giNMF算法降到的维数最小;而对于相同的降维维数,KL散度最小,也即误差最小。
3.2 通信能耗分析
假设接收和发送单位(bit)能耗为50 nJ/bit,传输数据矩阵M=2 000 bits,N=50。图4所示为giNMF算法与LEACH算法的通信能耗对比实验。从图4可见:giNMF算法能耗要低于LEACH算法,LEACH算法平均通信能耗是 giNMF算法 2倍以上。从而得出giNMF降维算法能够有效降低通信数据规模,去除通信数据的白噪声,实现节能的目的。

图3 降维效果比较Fig. 3 Comparison on compression effectiveness

图4 通信能耗对比实验Fig. 4 Comparison on communication energy consumption
3.3 网络生命周期分析
模拟实验环境为一个100 m×100 m的区域,监控环境的温湿度信息,传感器节点数量N=100,传感器节点与簇首之间采用单跳通信,传感器节点的白噪音服从高斯分布 N(0,2.25),每个传感器结点的初始值为0.5 J,比较对象为文献[15]中的LEACH算法。评价无线传感器网络温湿度监控系统的重要指标是系统生命周期,生命周期越长,系统越好。从图5可见:采用giNMF算法的系统生命周期比LEACH算法的系统生命周期要提高50%左右。

图5 网络生命周期对比实验Fig. 5 Comparison on network lifetime
图5所示为giNMF算法和LEACH算法的网络生存时间进行比较,图5显示了网络中存活节点的变化情况,随着死亡节点数目增多,节点死亡速度均出现加快的趋势。LEACH算法最早出现死亡节点,giNMF约在1 000轮出现第1个死亡节点。LEACH算法在1 300轮左右网络节点全部死亡,giNMF在1 800轮左右节点全部死亡,本文算法网络生命周期最长。比较结果表明:本文算法能够有效地延长网络生存时间。
4 结论
(1) 提出一种基于广义逆非负矩阵分解的无线传感器网络节能通信算法,有效降低通信数据量,从而实现能耗降低。该算法特点是:具有较强的泛化能力,具备通信协议无关性,因此,具有广泛的应用范围;高维数据压缩准确、误差低,压缩后的数据能够真实描述原始状态,具备降维不失真性。
(2) 分别从降维效果、通信能耗、网络生命周期3个角度进行对比分析。仿真实验结果表明:giNMF算法能够对通信数据进行有效压缩,从而降低通信能耗,延长网络生命周期,达到节能的目的。
[1] Mottola L, Picco G P. Programming wireless sensor networks:fundamental concepts and state of the art[J]. ACM Computing Surveys, 2011, 43(3): 19-24.
[2] Srivastava N. Challenges of next-generation wireless sensor networks and its impact on society[J]. Journal of Telecommunication, 2010, 1(1): 128-133.
[3] Keeler H P, Taylor P G. A model framework for greedy routing in a sensor network with a stochastic power scheme[J]. ACM Transactions on Sensor Networks, 2011, 7(4): 34-37.
[4] Veeravalli V V, Varshney P K. Distributed inference in wireless sensor networks[J]. Philosophical transactions of the Royal Society A, 2012, 370(1958): 100-117.
[5] WANG Tian, WANG Guojun, GUO Minyi, et al.Hash-area-based data dissemination protocol in wireless sensor networks[J]. J Cent South Univ Technol, 2008, 15(3): 392-398.
[6] Fuemmeler J A, Atia G, Veeravalli V V. Sleep control for tracking in sensor networks[J]. IEEE Transactions on Signal Processing, 2011, 59(9): 4354-4366.
[7] Han J A, Jeon W S, Jeong D G. Energy-efficient channel management scheme for cognitive radio sensor networks[J].IEEE Transactions on Vehicular Technology, 2011, 60(4):1905-1910.
[8] Varshney K R, Willsky A S. Linear dimensionality reduction for margin-based classification: High-dimensional data and sensor networks[J]. IEEE Transactions on Signal Processing, 2011,59(6): 2496-2512.
[9] Hu W Z, Hao Y, Huang L. Multidimensional data reduction based on compressed sensing for sensor network[M]//Zhang Y.Future Wireless Networks and Information Systems. Heidelberg:Springer, 2012: 721-728.
[10] Lee D D, Seung H S. Learning the parts of objects by non-negative matrix factorization[J]. Nature, 1999, 401:788-791.
[11] Kromer P, Platos J, Snasel V. Fast dimension reduction based on NMF[C]//Proceedings of the 5th International Conference on Advances in Computation and Intelligence. Heidelberg: Springer,2010: 424-433.
[12] Zhou G, Cichocki A, Xie S. Fast nonnegative matrix/tensor factorization based on low-rank approximation[J]. IEEE Transactions on Signal Processing, 2012, 60(6): 2928-2940.
[13] Ben I A, Greville T N E. Generalized inverses: theory and applications[M]. Heidelberg: Springer, 2003: 182-224.
[14] Wang A Y. Low Power RF Transceiver Modeling and Design for Wireless Sensors Network[D]. Boston: Massachusetts Institute of Technology. Department of Electrical Engineering and Computer Science, 2005: 55-77.
[15] Heinzelman W R, Chandrakasan A, Balakrishnan H.Energy-Efficient Communication Protocol for Wireless Microsensor Networks[C]//Proceedings of the 33rd Annual Hawaii International Conference on System Sciences. Hawaii:IEEE Press, 2000: 3005-3014.
