基于ANSYS/LS-DYNA的V150油套管热矫直残余应力
2013-06-04李阳华李红英尹浩邓云喆谢凯意
李阳华 ,李红英,尹浩,邓云喆,谢凯意
(1. 中南大学 有色金属材料科学与工程教育部重点实验室,湖南 长沙,410083;2. 衡阳华菱钢管有限公司 技术中心,湖南 衡阳,421001;3. 三一集团 研究总院研发试验中心,湖南 长沙,410100)
随着石油工业的发展,深井、超深井油田相继增多,开采环境趋向恶劣化,井身结构更加复杂,套管层次增多,井下工况存在较多的不确定性,套管脱扣、螺纹密度失效、磨损、挤毁和腐蚀等损伤失效案例时有发生,极易导致井眼失稳、储层伤害、严重的掉井甚至发生毁井事故,造成重大经济损失。因此,对油套管的服役性能提出了越来越高的要求,必须抗拉、抗压、抗挤毁、抗腐蚀、抗疲劳,此外,还要有较好的耐磨性能、接箍强度和整体密封性[1,2]。油套管经轧制后,往往存在纵向弯曲和横截面圆度误差,必须经过矫直来消除或减小,一般采用 2-2-2型六斜辊矫直机进行热矫直,因为冷矫直会产生较大的残余应力,而矫直后的残余应力及其分布对套管的抗拉、抗压、抗挤毁、抗疲劳、抗腐蚀等性能的影响极大[3-5]。由于钢管在三对旋转的辊子间被反复压扁和弯曲,应力-应变规律极其复杂,实验测量油套管残余应力不仅耗资大,而且很难得到残余应力的分布规律[6-8],采用有限元模拟的方法可以解决这个问题[9]。徐勇等[10-11]通过有限元软件MARC建立P110油套管冷矫直二维模型,研究残余应力沿管体壁厚的分布规律,李连进[12-13]利用有限元软件ANSYS建立P110油套管热矫直的三维模型,研究矫直量与最大残余应力的关系。但是,对残余应力沿轴向分布规律的研究很少,对于比P110更高钢级的V150油套管的矫直后残余应力的研究未见文献报道。本文作者通过有限元软件ANSYS/LS-DYNA建立 V150油套管的三维矫直模型,分析矫直后环向和轴向残余应力的分布情况,并与实验测量结果进行对比,为油套管矫直工艺优化提供理论依据。
1 有限元模型
1.1 显式动力学算法
油套管矫直过程是一个瞬态响应的过程,广泛采用显式直接积分法进行求解[14-16]。采用显式直接积分法,在每一个时间增量内,需要求解系统的运动方程,如下式所示:
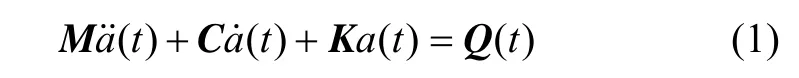
式中:()a t˙,()a t˙和a(t)分别为系统的节点加速度、节点速度和节点位移;M,C,K和Q(t)分别为系统的质量矩阵、阻尼矩阵、刚度矩阵和节点载荷向量。
由中心差分法进行显式时间积分,得到速度和位移表达式如下:
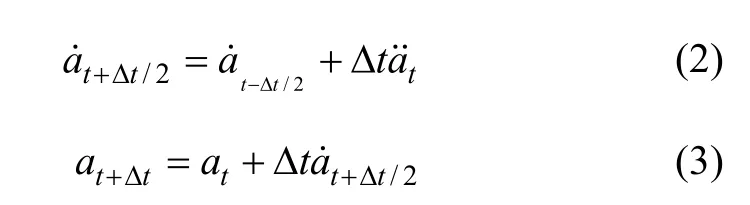
三维矫直有限元模型规模大,涉及到材料非线性、几何非线性以及状态非线性,具有高度非线性的特点,使用隐式算法存在占用内存多,迭代收敛困难,运算缓慢的问题。由式(2)和(3)可以看出:动力显式算法不用求解任何矩阵形式的系统方程,不涉及复杂的求解收敛问题,占用内存少,单次求解速度很快,易于实现大规模的计算,因此,应用显式动力学算法计算此类问题效率较高。
1.2 材料规格与性能参数
V150实验钢管的尺寸规格为φ 177.8 mm×12.65 mm,全长为11.2 m,其热矫直温度为420 ℃,在Instron 3369力学试验机上进行拉伸实验,图1所示为420 ℃下实验钢管的真应力-真应变曲线。由图 1可知:实验钢管的屈服强度为903 MPa,弹性模量为183 720 MPa,切线模量为2 030 MPa,表1所示为模拟需要的材料属性参数。
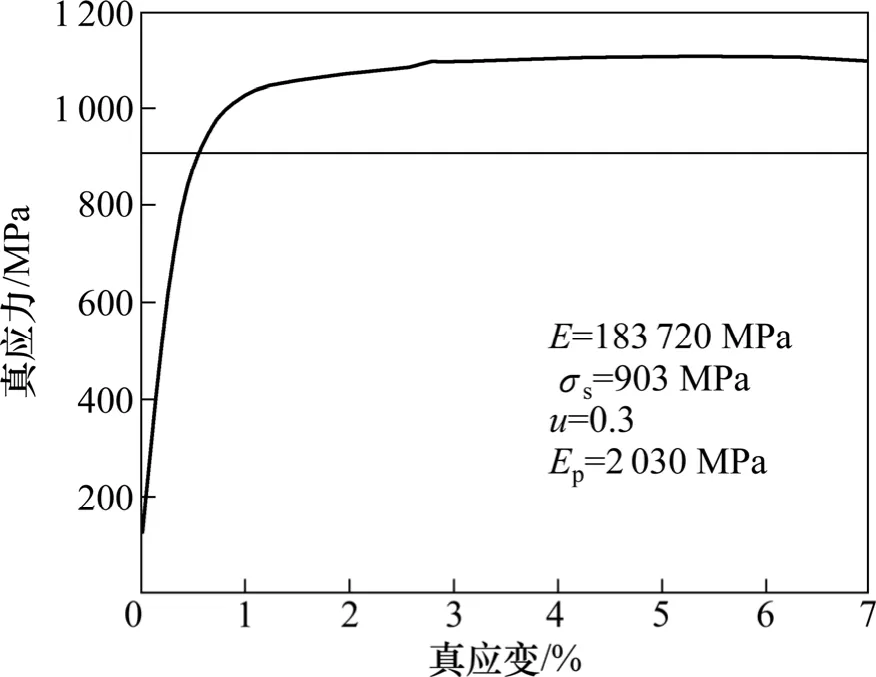
图1 实验钢管的真应力-真应变曲线Fig. 1 True stress-true strain curves of experimental casing

表1 实验钢管的材料属性参数Table 1 Parameters of material properties of experimental casing
1.3 网格划分
采用映射方法划分网格,径向分为5层,环向分为60层,对于轴向网格划分,在重点分析管段采用5 mm划分,其他部分采用15 mm和30 mm混合划分。矫直辊和传送辊可视作刚体单元,但为了更好地描述其几何形状,其网格划分不能太粗化,矫直辊全局尺寸划分为20 mm,传送辊圆周尺寸划分为5 mm,轴向网格划分为1份。图2所示为采用实体单元模拟矫直管和矫直辊的网格划分,矫直管被划分为45 600个实体单元。
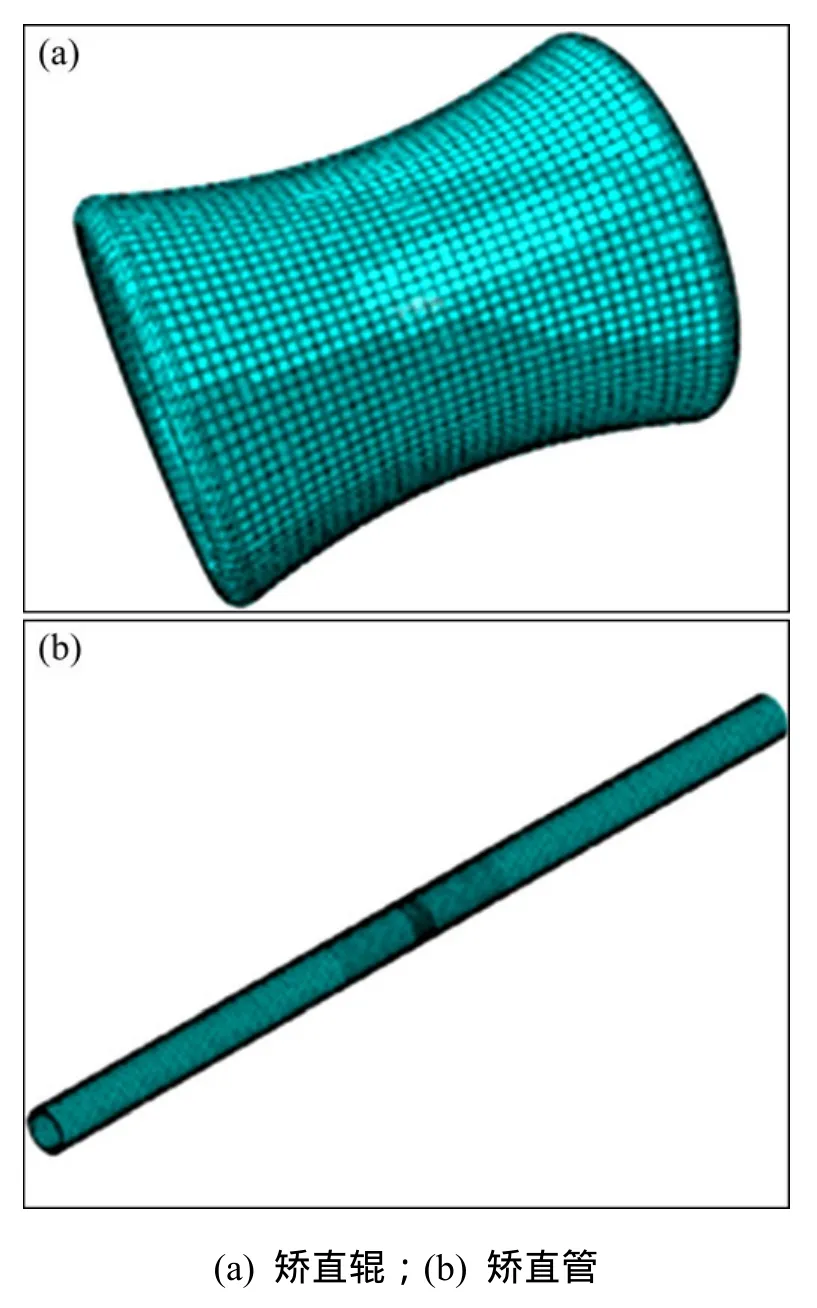
图2 矫直辊和矫直管网格划分Fig. 2 Meshes of roller and casing
1.4 接触条件处理
选择矫直管作为接触从面,矫直辊作为目标主面,接触方式采用自动面-面接触,为更好实现收敛,打开 SMOOTH选项对矫直辊模型进行光滑处理。矫直管与矫直辊间的摩擦因数对于矫直过程的分析影响很大,本研究通过对比用有限元计算的螺距值和实测值来确定摩擦因数的大小。工厂提供的矫直辊的倾斜角是33.5°,矫直管的外径是177.8 mm,矫直速率为650 mm/s,实测的螺距平均值为371.7 mm。图3所示为采用不同摩擦因数模拟计算出的结果,当摩擦因数为0.20时,螺距值最大,为369.36 mm,与实测值最接近,因此确定摩擦因数为0.20。矫直辊的最优倾斜角为32°,相应螺距为349 mm。
1.5 模型求解
三维矫直模拟极为耗时,在频率为 2.6 GHz的AMD单核处理器上,完成一次计算约500 h,因此在普通计算机上模拟时间太长,计算代价很大。本课题在高性能计算机平台上进行模拟计算,每个矫直模型都采用8个CPU进行分布式并行运算,大大节省了计算时间,完成一次计算的时间降低为100 h左右,加速比约为5。图4所示为矫直管通过矫直辊时的应力分布图,通过模拟可以精确获得矫直过程中应力应变的变化以及矫直后残余应力的分布规律。
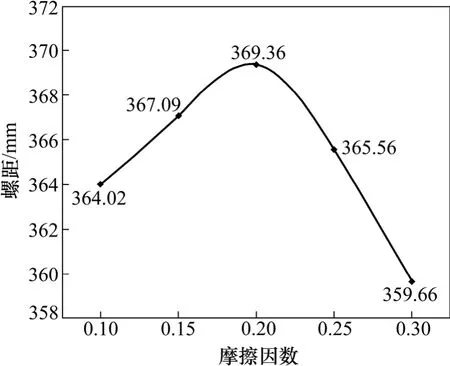
图3 不同螺距对应的摩擦因数Fig. 3 Frictional coefficient of different pitches
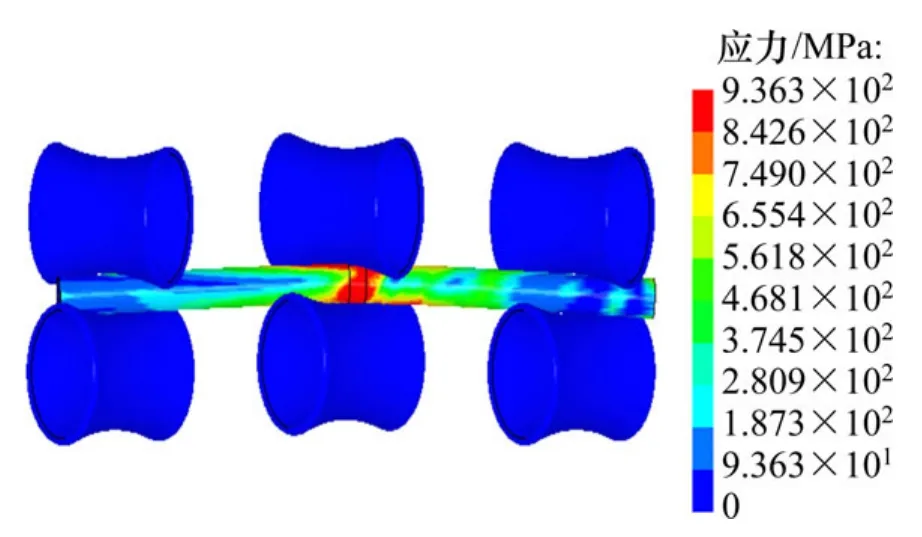
图4 矫直过程应力分布Fig. 4 Distribution of roll-straightening process
2 残余应力分析
矫直后钢管会存在残余应力,由于径向残余应力相对于环向和轴向的残余应力来说非常小,本文只研究环向和轴向残余应力的分布规律。
2.1 环向残余应力分析
图5所示为矫直后钢管的环向残余应力分布。由图 5(a)可知:钢管外表面环向残余应力均为拉应力,数值在200~500 MPa之间,内表面环向残余应力均为压应力,数值在-130~-480 MPa之间。沿轴向,内外表面的环向残余应力均形成螺旋接触带,螺旋接触带与管体轴向方向的夹角约为58 °,满足与矫直辊的倾斜角32 °互余的条件,同时,相邻的2个螺旋接触带之间的距离约为 350 mm,其距离非常接近油套管螺距(349 mm)。图5(b)所示为管体某横截面环向残余应力的分布,横截面大部分区域环向残余应力在-200~200 MPa 之间,在 45°~160°之间应力较大,最大拉应力达到360 MPa,最大压应力达到-370 MPa。
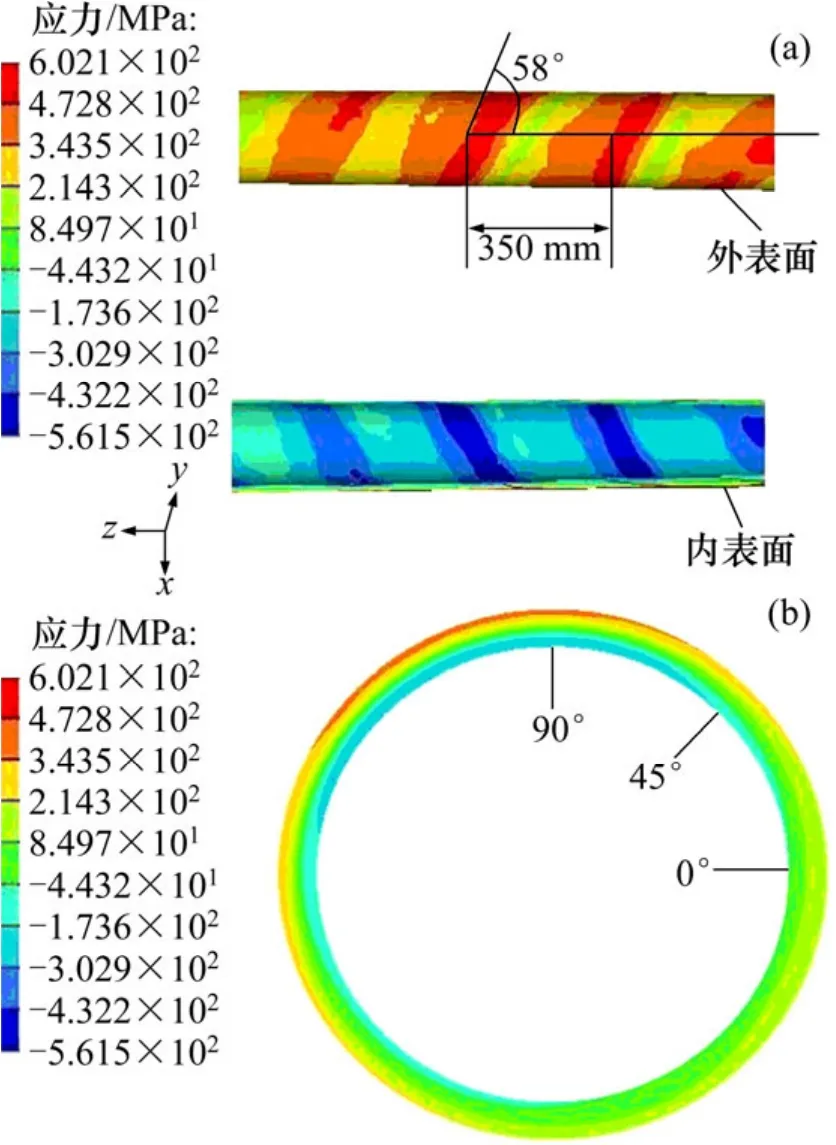
图5 环向残余应力分布Fig. 5 Distribution of circumferential residual stress
图6所示为环向残余应力沿轴向、横截面壁厚以及圆周方向的分布。由图 6(a)可知:矫直管内外表面环向残余应力都沿轴向方向呈波浪形状分布,相邻波峰(波谷)间距约为350 mm,且分布规律大致关于X轴对称,外表面环向残余拉应力的波峰(波谷)对应于内表面环向残余压应力的波谷(波峰)。由图 6(b)可知:沿壁厚方向,0°,45°和90°处环向残余应力均是由外表面的拉应力近似线性地过渡到内表面的压应力。由图 6(c)可知,外圆周环向残余应力均为拉应力,内圆周环向残余应力均为压应力,沿圆周方向,内外圆周环向残余应力关于X轴对称分布,对称性较好。
2.2 轴向残余应力分析
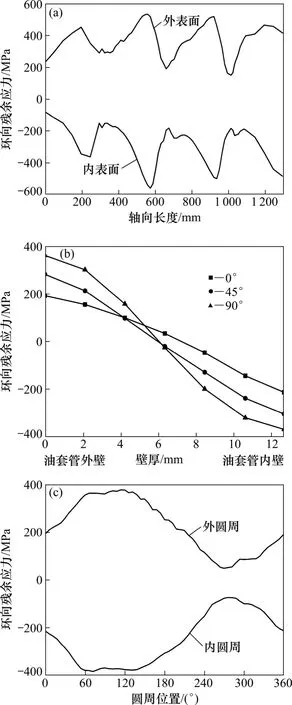
图6 环向残余应力分布曲线Fig. 6 Distribution curves of circumferential residual stress
图7所示为矫直后钢管轴向残余应力分布。由图7(a)可知:管体大部分区域的轴向残余应力在-175~300 MPa之间,外表面轴向残余应力几乎全为拉应力,数值在150~300 MPa之间,内表面则拉应力和压应力并存,数值在-175~75 MPa之间。沿轴向,轴向残余应力形成了不太明显的螺旋接触带,螺旋接触带与管体轴向夹角接近58 °,满足与矫直辊的倾斜角32 °互余的条件,相邻螺旋接触带的间距(350 mm)也近似等于螺距(349 mm)。图7(b)所示为矫直管横截面轴向残余应力分布。由图7(b)可知:轴向残余应力的分布很不均匀,外表面轴向残余应力均为拉应力,其余部分大多为压应力,最大压应力出现在 45°和 200°附近靠近壁厚中部的位置,最大值为-300 MPa。

图7 轴向残余应力分布Fig. 7 Distribution of longitudinal residual stress
图8所示为轴向残余应力沿轴向、横截面壁厚以及圆周方向的分布曲线。由图 8(a)可知:轴向残余应力沿轴向的分布规律与环向残余应力沿轴向的分布规律相似,内外表面轴向残余应力沿轴向呈波浪形分布,大致关于Y=100 MPa对称,相邻波峰(波谷)的间距为350 mm,与螺距相近。外表面轴向残余应力都是拉应力,在75~300 MPa之间,内表面轴向残余应力既有压应力又有拉应力,沿轴向位移交替循环,数值不大,在-75~100 MPa之间。由图8(b)可知:轴向残余应力沿壁厚方向的分布很不均匀,而且在圆周不同角度轴向残余应力沿壁厚的分布表现出不同的规律,在0°方向,轴向残余应力内外表面均为拉应力,而壁厚中部为压应力,但压应力很小,在120°方向,轴向残余应力均为压应力,应力变化比较平缓,应力不大,在-10~-150 MPa之间,在200°方向,轴向残余应力先由外表面的拉应力逐渐过渡到压应力,压应力沿壁厚先增大后减小,最大压应力为-200 MPa。由图8(c)可知:沿圆周方向,轴向残余应力的分布也不均匀,外圆周轴向残余应力几乎全为拉应力,在-15~300 MPa之间,内圆周轴向残余应力表现为拉、压并存,数值在-170~130 MPa之间。
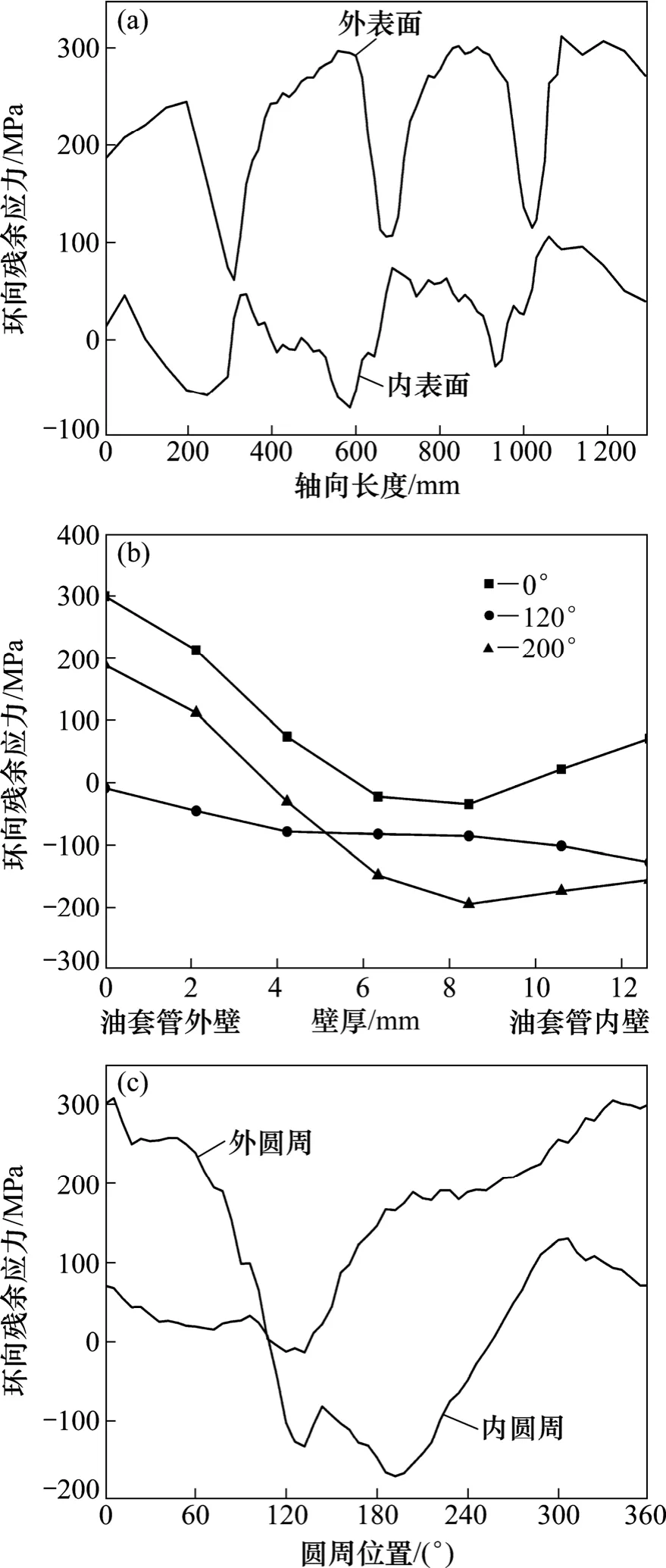
图8 轴向残余应力分布曲线Fig. 8 Distribution curves of longitudinal residual stresses
3 残余应力实验测量
利用 X线衍射法测量油套管内表面环向残余应力,图9所示为管体部位残余应力测量位置示意图。在管体部位取3个截面(C1,C2和C3),每个截面内均布4个测量点(A,B,C和D),用盐酸清除测量点附近(15 mm×15 mm范围内)表面氧化铁皮,用酒精擦洗干净。采用sin2ψ法,选用不同的X线入射角(0°,15°,30°和 45°),使用 Cr 靶 Kα辐射(211)面的衍射线[17-18]。
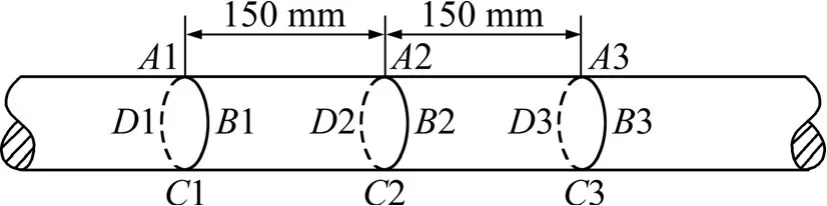
图9 残余应力测量位置Fig. 9 Location for residual stresses measurement
当管坯的原始形状误差较大时,矫直时变形大,残余应力相应也大,反之残余应力较小。由于生产工艺的复杂性,钢管的形状精度很难保证,即使是同一批次的管材,其平直度和椭圆度也可能相差很大,不可能针对每根钢管设定不同的工艺参数,即使是同一根钢管,不同部分的形状精度也难以相同,导致矫直管不同部位的残余应力相差很大。表2所示为矫直管内表面的环向残余应力测量值,在-189~-489 MPa之间变化,模拟值在-130~-480 MPa之间,两者吻合较好,表明建立的矫直模型是可靠的。
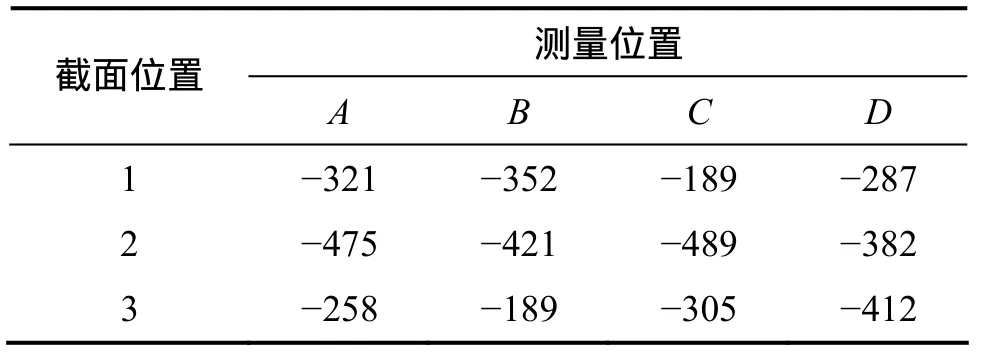
表2 环向残余应力Table 2 Circumferential residual stresses MPa
4 结论
(1) 矫直管环向和轴向残余应力沿轴向均表现出螺旋接触带的现象,螺旋接触带与管体轴向成 58°的夹角,与矫直辊倾角互余,相邻的2个螺旋接触带之间的距离约为 350 mm,基本等于矫直管的螺距(349 mm)。
(2) 环向残余应力表现出外拉内压的规律,沿壁厚由拉应力过渡到压应力,沿轴向呈波浪状分布;外表面的轴向残余应力以拉应力为主,内表面的轴向残余应力为拉、压应力并存,压应力极大值出现在壁厚中部。
(3) 利用X线衍射法测量矫直管内表面环向残余应力,实测值在-189~-489 MPa之间,模拟数值在-130~-480 MPa之间,两者吻合良好,表明建立的矫直模型是可靠的。
[1] 韩正磊. 深井超深井钻井技术在我国石油工程中的现状与发展[J]. 中国石油和化工标准与质量, 2011(12): 169.HEN Zhenglei. The current situation and development of deep and super-deep wells drilling technology on petroleum in China[J]. China Petroleum and Chemical Standard and Quality,2011, (12): 169.
[2] 马开华, 刘修善. 深井超深井钻井新技术[M]. 北京: 中国石化出版社, 2005: 3-15.MA Kaihua, LIU Xiushan. New drilling techniques of deep and super-deep wells[M]. Beijing: China Petrochemical Press, 2005:3-15.
[3] 申昭熙, 丁学光, 李东风, 等. ERW套管与无缝套管残余应力及外压挤毁试验研究[J]. 焊管, 2007, 30(4): 31-33.SHEN Zhaoxi, DING Xueguang, LI Dongfeng, et al. Study of residual stress and collapse of ERW and seamless casing[J].Welded Pipe and Tube, 2007, 30(4): 31-33.
[4] 尹宝俊, 赵文轸, 张西明, 等. 油井套管失效破裂原因分析[J].石油化工腐蚀与防护, 2004, 21(6): 27-30.YIN Baojun, ZHAO Wenzhen, ZHANG Ximing, et al. Analysis of cracking failure of oil well conduit[J]. Petrochemical Corrosion and Protection, 2004, 21(6): 27-30.
[5] 张洁, 李连进, 屠浩, 等. 残余应力对石油套管承载能力的影响分析[J]. 天津理工学院学报, 2004, 20(4): 11-14.ZHANG Jie, LI Lianjin, TU Hao, et al. Analyse the influence of the residual stress on the casing pipe’s loading ability[J]. Journal of Tianjin Institute of Technology, 2004, 20(4): 11-14.
[6] 刘倩倩, 刘兆山, 宋森, 等. 残余应力测量研究现状综述[J].机床与液压, 2011, 39(11): 135-138.LIU Qianqian, LIU Zhaoshan, SONG Sen, et al. Research status of measurement for residual stress[J]. Machine Tool &Hydraulics, 2011, 39(11): 135-138.
[7] 王庆明, 孙渊. 残余应力测试技术的进展与动向[J]. 机电工程, 2011, 28(1): 11-15.WANG Qingming, SUN Yuan. Research development on the test methods of residual stress[J]. Journal of Mechanical & Electrical Engineering, 2011, 28(1): 11-15.
[8] 周磊, 余忠华. 电梯导轨侧弯矫直建模仿真与实验[J]. 中南大学学报: 自然科学版, 2011, 42(6): 1636-1642.ZHOU Lei, YU Zhonghua. Modeling, simulation and experiment for straightening lateral bending of elevator guide rail[J]. Journal of Central South University: Science and Technology, 2011,42(6): 1636-1642.
[9] 李连进, 沈淑君. 数值仿真技术在石油套管制造中应用的展望[J]. 天津冶金, 2004(6): 35-37.LI Lianjin, SHEN Shujun. Prospect of application of numerical simulation technology to the casing pipe manufacture[J]. Tianjin Metallurgy, 2004(6): 35-37.
[10] 徐勇, 程先华. 钢管压扁矫正残余应力分析[J]. 上海交通大学学报, 2003, 37(10): 1526-1528.XU Yong, CHENG Xianhua. Residual stress formation during the crushing of tube[J]. Journal of Shanghai Jiaotong University,2003, 37(10): 1526-1528.
[11] 徐勇, 程先华. P110套管冷矫残余应力模拟分析[J]. 钢铁,2004, 39(1): 30-32.XU Yong, CHENG Xianhua. Simulation analysis of residual stress for cold straightening P110 casing[J]. Iron and Steel, 2004,39(1): 30-32.
[12] 李连进. 石油套管热矫直残余应力的计算机模拟[J]. 重型机械, 2005(4): 43-45.LI Lianjin. Simulation of thermal straightening residual stress of the oil casing[J]. Heavy Machinery, 2005(4): 43-45.
[13] 李连进. 用有限元方法分析石油套管矫直产生的残余应力[J].钢管, 2006, 35(2): 29-32.LI Lianjin. Residual stress analysis of oil casing during straightening by finite element method[J]. Steel Pipe, 2006,35(2): 29-32.
[14] 赵海鸥. LS-DYNA动力分析指南[M]. 北京: 兵器工业出版社,2003: 7-11.ZHAO Haiou. Guide of LS-DYNA dynamic analysis[M].Beijing: Weapons Industry Press, 2003: 7-11.
[15] Zienkiewicz O C. The finite element method: its basis and fundamentals 6th ed[M]. Beijing: World Publishing Corporation,2008: 103-134.
[16] 龚海, 吴运新, 廖凯. 不同淬火工艺对 7075铝合金厚板残余应力的影响[J]. 中南大学学报: 自然科学版, 2010, 41(4):1354-1359.GONG Hai, WU Yunxin, LIAO Kai. Influence of different quenching techniques on residual stress of 7075 aluminum alloy thick-plate[J]. Journal of Central South University: Science and Technology, 2010, 41(4): 1354-1359.
[17] 周玉. 材料分析方法[M]. 北京: 机械工业出版社, 2006:79-94.ZHOU Yu. Methods for material analysis[M]. Beijing: China Machine Press, 2006: 79-94.
[18] 张亦良, 刘金艳, 徐学东. 不锈钢X射线应力测量[J]. 北京工业大学学报, 2010, 36(9): 1165-1173.ZHANG Yiliang, LIU Jinyan, XU Xuedong. X-ray stress measurement of stainless steel[J]. Journal of Beijing University of Technology, 2010, 36(9): 1165-1173.
