激发习题活力 引领学生成长

史厚勇

（南通市城西小学，江苏 南通 226000）

数学习题是数学课本的重要组成部分，是学生知识内化、能力形成的载体，其重要成为大家的共识。然而在实际教育教学中，数学习题往往定位在知识与技能上，忽视情感、态度和价值观、忽视过程与方法，使得数学习题逐渐变得单调、枯燥，毫无生机。作为教师，应该重新审视习题的作用，充分挖掘习题的潜在功能，激活习题鲜活的生命力，引领学生在习题的解读中发现、体验、感悟，让习题可观、可感、可亲。

一、发现解题之“美”

数学是富有魅力的学科，虽没有鲜艳的色彩，没有美妙的声音，没有动感的画面，却有一种独特的美。数学习题孕育其中，质朴，深沉，令人赏心悦目。在教学中，教师应让孩子通过数学习题感受更多的数学意义，体会数学的神奇，发现数学习题的美，引发学生美的享受。

【片段实录】

例如，教学苏教版二年级上册第84页第7题

师：同学们做完了三组题，你有什么发现？

生1：我发现每组两道题的得数是一样的。

生2：我发现下面乘法中两个数都一样。

师：同学们观察得真仔细！为什么每组两道题的得数一样呢？

生3：我知道。第一道题中，3比1大，可以借1个给1，这样两个数都变成了2，也就是1+3=2+2，2个2相加就是2×2=4。

生4：我也是这样想的。在1+3+5中，从5里面借给2给1，这样三个数都变成了3，也就是1+3+5=3+3+3，3 个 3相加就是 3×3=9。

生5：第三组，5分1个给3,7分3个给1，这样就是 4个 4，也就是 4×4=16。

师：同学们真不简单！你能创造出这样的算式吗？（部分学生跃跃欲试）先在小组里面说一说，再写一写。

生6：我们组创造了这样一组算式：1+3+5+7+9=25，5×5=25。

生 7：我们组创造的是：1+3+5+7+9+11=36，6×6=36。

生 8：我们是 1+3+5+7+9+11+13=49，7×7=49。

……

（教师根据学生的回答，板书）

生9：我发现他们写的数都有规律，都是从1开始写的。我觉得这样的算式很多，写不完。

生10：我发现个秘密，就是加数有几个就是几乘几。

师：你们认同他们的观点吗？我们不妨听听他们的解释。

生 9：你看在加法中是 1、3、5、7、9，数在逐渐变大，每两个数之间相差2。这样的算式可以写无数个。

生 10：1+3+5是 3个数，就是3×3；1+3+5+7是 4个数就是4×4；……1+3+5+7+9+11+13是7个数，就是7×7。

师：真的有这样的秘密吗？认真观察，小组内讨论，验证有没有这样的秘密。

（学生在小组内讨论，有的拿出笔写出多个类似的算式进行计算，不一会儿举手的学生越来越多，情绪高涨，显得特别兴奋）

师：有这样的秘密吗？（有），那么你们认为“1+3+5+7+9+11+13+15+17”应该等于？

（学生自觉地数了起来，然后齐声答道9×9）

师：对吗？能算一算吗？

（学生一起计算1+3+5+7+9+11+13+15+17=81，9×9=81）

师：看来，大家发现的秘密还真行。如果老师写出8×8，你知道应该等于1+3+5……加到几？

（学生掰手指数数）

生（齐）：1+3+5+7+9+11+13+15。

师：为什么不往下加了？

生（齐）：已经有8个数了。

师：对吗？验证看看。

（学生计算，得到两边结果都是64）

师：同学们做了三组题，发现了题中的秘密，可是老师还有一个疑惑，是不是所有的类似加法都有这样的秘密。

（学生听后，有些说“有”，有些说“没有”，有的则安静，产生疑惑）

师：看来同学们也不敢肯定，我们不妨自己举例子试试看。

（学生小组内写算式观察）

生11：我们组写的是1+2+3+4+5，不能写成两个相同的数相乘，但可以写成3×5=15。

生12：我们写的是2+4+6，也不能写成两个相同的数相乘，但可以写成4×3=12。

生13:我们写的是1+4+7，写成两个数相乘是4×3，不能写成两个相同的数相乘。

生14：我们组写得比较多。2+4=3×2，2+4+6=4×3，2+4+6+8=5×4，2+4+6+8+10=6×5……我们发现虽然不能写成两个相同的数相乘，但是发现实际上是用中间的数乘加数的个数。

师：先不要忙着下结论，小组内再多写几个这样算式验证一下。

（学生在小组内书写，不一会儿争先恐后地要发言）

师：你们写的算式都有这样的秘密吗？

生（齐）：有。

师：同学们的眼光真不简单，课后不妨多写一些不同的算式，让我们多发现一些数学的秘密……

苏教版教材中设置此题，从运算的角度来思考，二年级学生在掌握了乘法口诀并且已经熟练计算简单的加减法的基础上，能够快速的完成解答。然而，此题并非局限于此，在教学中，需要将习题从更高层面上审视，引发学生的思考，引导学生去发现、去提升。在我们看来，学生的发现也许是那么的浅显，也许是那么的不严密，也许是那么的微不足道。然而，教师从题组中引导学生发现、提升，将习题进行创造性的再生，将习题富有了生命力，引发学生发现、感悟。学生经历其中，不知不觉获得情感的、精神的愉悦，而且生机勃勃，鲜活亮丽，这是简单的习题计算所不能达到的。

二、体验改题之“变”

在新课程理念下，教师要紧紧把握习题的桥梁作用，让桥梁变得更宽，更广，因此需要教师加深对教材例题的理解和把握，引导学生体验习题的“变”，在“变”中提升。

例如，教学苏教版五年级下册“有关圆的组合图形的面积计算”，教材提供的是圆环，通过圆环面积计算的推导，掌握其计算方法。这对学生而言比较简单，作为教者应把教学目标进行延伸，延伸学生的知识广度，沟通、形成知识网络，进一步积累学习经验。

【片段实录】

教师首先出示圆环，对圆环的知识进行简单的介绍，引导学生初步认识内圆和外圆，并发现圆环同一圆心的特点，同时引导学生寻找生活中圆环，如游泳圈、水管龙头的垫圈、汽车轮胎等，并学会画圆环，然后出示例题。

师：你能求出这个环形的面积吗？（出示课本例10）

师：读题并观察圆环，你有什么发现？

生1：我发现外圆半径就是指外面大圆的半径，内圆半径就是指里面空白部分小圆的半径？

生2：我发现求圆环铁片的面积只要用大圆的面积减去里面空白小圆的面积就行了。

师：是这样吗？

（学生再次观察圆环，然后小组内讨论得到一致的看法）

师：看来大家对求圆环的面积都有了共同认识，不妨自己算一算。

（学生独立计算，教师个别指导，并集体订正）

师：你是怎样列式的，要求圆环的面积需要哪些条件？

生3：需要知道外圆的半径和内圆的半径，然而分别求出外圆的面积和内圆的面积，再相减即可。列式为3.14×102－3.14×62=200.96 平方厘米。

师：不错，可是老师发现有同学这样列式3.14×（102－62）也得到200.96平方厘米，你们认为对吗？

生4：我认为对的，实际上是运用了乘法分配律，把3.14×102－3.14×62这个算式进行了整理，而且比原来的算式更简便。

师：有道理，看来我们在计算中还要多观察。下面一题，你能做出来吗？

出示：求下面环形的面积。（单位：厘米）

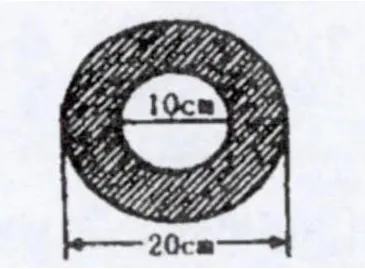
师：这个环形的面积是怎样计算的?

生5：这道题没有直接告诉我们外圆半径和内圆半径，但是知道外圆直径和内圆直径，因此可以先转化求出外圆半径和内圆半径，最后再求圆环面积。

师：缺少我们需要的条件，我们可以转化，找出我们需要的条件。如果老师把这个圆环对折，你能求出下面图形的面积吗？

出示：

师：如果我再对折一次怎样求阴影部分的面积？生7：用环形的面积乘。

师：你是怎么想的？

师“：头脑中有图”，对于我们解决问题有很大的帮助。下面一组题，你能求出阴影部分的面积吗？

出示：

生9：第一幅图，用大圆面积减去两个半圆的面积就能求出阴影部分的面积。

生10：第一幅图，用大圆面积减去一个小圆的面积就能求出阴影部分的面积。

师：你是怎样想的?

生11：两个小半圆正好可以拼成一个整圆。

师：真不错。

生12：第二幅图的阴影面积同第二幅图的思考方法一样。也是用大圆面积减去一个小圆的面积就能求出阴影部分的面积。

生13：第三幅图我觉得还是用大圆面积减去一个小圆的面积就能求出阴影部分的面积。

师：为什么？

生14：两个半环形，可以把它们拼成一个整环形。

师：（指着图形）这几个图形的阴影部分各不相同，计算方法怎么会一样呢?

生15：它们阴影的形状变了，但都包含在大圆内，所以计算的方法没有变，都是用大圆的面积减去空白部分的小圆面积求出阴影面积。

师：对。阴影的形状各不相同，但只要仔细观察，把图形进行适当的整理转化，就能找到不变的规律。你能说出下面阴影部分的面积该怎样计算？

出示：求下面阴影部分的面积。

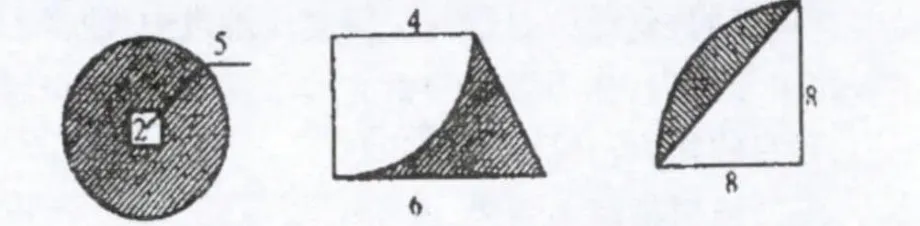
生16：第一幅图，是由一个圆和一个正方形组成的，正方形在圆的里面，因此阴影部分的面积是大圆面积减去正方形的面积。列式为3.14×52－22。

生17：第二幅图，大的图形是一个梯形，阴影部分的面积就是用梯形的面积减去圆的面积。

师：同学们观察得真仔细，虽然图形发生了变化，但是同学们的眼力真“神”！老师还想考考大家。

出示：

A．求下面图形中阴影面积。（单位：厘米）

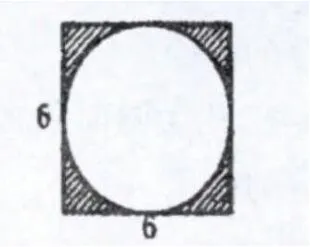
B．观察下面这组图形，不计算你能否判断出它们的阴影面积与上题的结果是否相等？为什么？

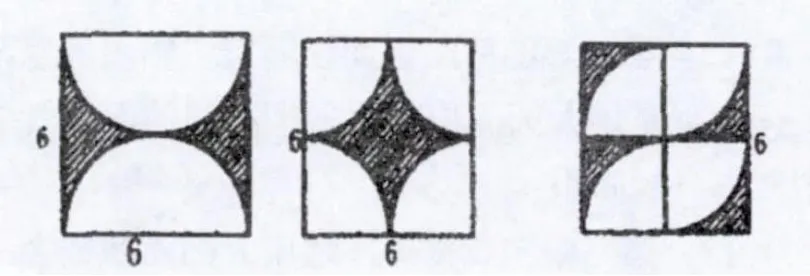
生19：相等。因为这一组图形的条件相同，阴影面积都包含在相等的正方形内，图中空白部分面积都可转化成直径与正方形边长相等的圆，都可按上题的计算方法用正方形的面积减去一个圆面积求得阴影面积。

生20：这几幅图中的阴影面积虽然形状变了，但都可以转化，解题思路和解题方法不变。

……

教学中通过对例题多角度，多方面的变式探索，有意识地引导学生从“变”的现象中发现“不变”的本质，从“不变”的本质中探索“变”的规律，变中求“活”，变中求“新”，变中求“异”，变中求“广”。学生由“点”到“面”的变化体验，在经历习题的层层变化推进中，使得习题彰显生命活力，从而激活学生的数学灵感，提高思维能力，自身的知识经验也得到充实。

三、感悟破题之“妙”

数学习题的重要作用是锻炼学生思维，引导学生掌握解题方法。然而在我看来，学生解题≠做题，而是通过解题过程内化知识。解题的关键在于“破题”，在“破”中享受思维，享受数学习题带来的乐趣。

例如，教学苏教版五年级上册“求小数的近似数”。

教材通过两次取近似数，引导学生比较其精确度，让学生理解“1.50比1.5更精确一些”，从而明确1.50中百分位上的0不能省略。在我看来，教材中的直接结论虽然能够对学生的理解起到强化作用，然而学生能否真正理解“为什么1.50比1.5的精确度更高”还值得推敲。在实际教学中，学生对1.50比1.5更精确的理解只是进行了语言重复，并没有内化，因此教学中我将“如何教”设计为预案的难点。

【片段实录】

（学生分别求出1.496亿千米分别精确到十分位、百分位的近似值1.5和1.50）

师：近似数1.50末尾的0能去掉吗？

生1：能去掉。因为根据小数的性质，小数部分末尾添上0或者去掉0，小数的大小不变，因此1.50去掉0，就可以写成1.5。

生2：不能去掉，1.50的计数单位是0.01,1.5的计数单位是0.1，它们的计数单位不同。

生3：能去掉。它们的计数虽然单位不同，但是结果是一样的，1.50里面有150个0.01，1.5里面有15个0.1，只是表示的数量不一样，其实并没有改变大小。

（三位学生的发言一时让所有的学生感到为难，对1.50末尾的0能否省略感到无所适从）

师：看来，1.50末尾的0能否省略还真难住了我们。我们不妨先放一放，先来看这样一个问题：一个两位小数，保留一位数是1.5，这个数原来可能是多少？

生4：一个两位数保留一位小数是1.5，那么我们要看百分位。这时候出现两种情况，进位与不进位。如果向十分位进位，那么原来就是1.4几，所以原来的两位小数从1.45到1.49之间。如果不进位，那么原来的两位小数是1.5几，从1.50到1.54之间。

师：也就是说，一个两位小数保留一位小数是1.5，原来的两位小数是在1.45到1.54之间。如果这是一个三位小数，保留一位小数后是1.5，这个三位小数可能是多少？

生5：用刚才的思路，我觉得可能是1.450到1.540之间。

生6：不对。应该是1.450到1.549之间。因为保留一位小数看百分位，跟千分位没有关系，所以千分位上可以是0到9的任意一个数字。

师：你们觉得哪位的观点正确。

（学生小组内讨论后，判定生6的观点正确）

师：你能在数轴上找出1.450和1.549吗？

（学生在给定的数轴上分别找出1.450和1.549，教师用括号线标出其取值的范围。如图）

师：从图上我们明显可以看出一个三位小数保留为一位小数的取值范围。如果还是一个三位小数保留两位小数后是1.50，那么原来的三位小数可能是多少？

生7：三位小数保留两位小数后是1.50，那么原来的三位小数在1.495到1.504之间。

师：你能在数轴上表示出它的取值范围吗？

（学生在数轴上分别找出1.495和1.504，教师用括号线标出其取值的范围。如图）

师：比较两张数轴图，你有什么发现？

生8：我发现两个三位数的取值范围不同。

生9：约等于1.5的取值范围比约等于1.50的取值范围大得多。

师：取值范围越来越小，说明近似数怎样？

生10：范围越来越小，说明近似数越来越接近原数，也就是近似数越来越精确。

师：现在我们来看1.50末尾的0能不能省略。

生齐：不能。

师：现在你能回答为什么吗？

生11：我觉得保留的位数越多越精确，因此这个小数末尾的0，不能省略。

生12:1.50虽然小数部分末尾有0，但是这里的0与小数的性质不同，这里的0表示的是精确度，所以不能省略。

教学中，笔者将难点采用数形结合的思想巧妙转化，通过“让图说话”的形式，变告诉为发现，变生硬为推理，将难点深深烙印在学生思维中，凸显破题中的妙趣横生。

学生刚学过分数乘法，感到无法解决，因此面露难色。执教时，笔者将此题进行了分解：

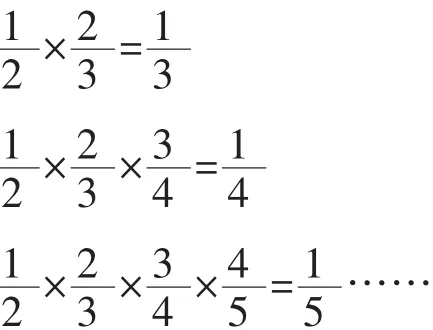
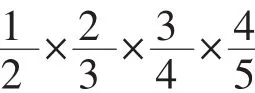
学生在教师的引领下，通过分解思考，从简单中发现，再运用到题中，使思路变得简单而巧妙。其过程就像呼吸那样流畅、自然，学生在解题中也不知不觉体味到数学的“妙”。

数学习题作为知识的载体，是可见的，然而其内在价值则隐喻其中。作为教师要充分解读习题，从习题中挖掘隐性的、潜在的数学价值，激活习题的内在活力，让习题变得鲜活，让习题变得饱满，让习题蕴含生命力，促进学生知识、能力、情感的协调成长。