矢量水听器相关性噪声的数值仿真方法

王绪虎, 陈建峰, 安芹力



矢量水听器相关性噪声的数值仿真方法

王绪虎1, 2, 陈建峰1, 安芹力1

(1. 西北工业大学 航海学院, 陕西 西安, 710072; 2. 曲阜师范大学 物理工程学院, 山东 曲阜, 273165)

矢量水听器阵列优化设计、性能分析和信号处理系统仿真中, 需要知道阵列输出噪声的协方差矩阵等信息。分析了各向同性噪声场中矢量水听器的相关性, 得出了矢量水听器的自相关和互相关函数的一般表达式。结合概率分析, 给出了一种简单的各向同性噪声场的数值仿真方法。仿真结果表明, 文中所给方法产生的矢量水听器噪声的相关性与理论值吻合良好, 可为矢量水听器阵列的优化设计和矢量阵列信号处理系统的仿真分析提供准确的数值噪声。

矢量水听器; 各向同性噪声; 相关性; 数值仿真

0 引言

矢量水听器是由声压水听器和振速传感器组合而成, 可同时测量声场中的标量信息(声压)和矢量信息(振速), 它具有良好的与频率无关的偶极子指向性和抑制各向同性噪声等优点, 近年来受到水声工作者的广泛关注[1-2]。

近20年来国内外学者对矢量水听器开展了多方面的研究。Berliner和Wong在20世纪90年代针对矢量水听器的设计、性能分析和工程应用等方面进行了相关研究[3-4]。Nehorai, Cray和Hawkes对矢量水听器及其阵列的目标检测和方位估计的算法进行了研究, 并对部分算法进行了性能分析[5-7]。2007年, 美国已经将矢量水听器拖曳阵装备到海军中, 并申请了相关专利[8-9]。还有学者对高阶组合水听器系列进行了研究[10-12]。

国内从20世纪90年代以来, 开展矢量水听器及其应用的相关研究。贾志富在矢量水听器的制作及测量方面取得了系列成果[13-14]。惠俊英、杨德森和孙贵青等人针对矢量水听器及矢量水听器阵列的噪声测量、目标检测和方位估计等技术进行了相关研究[15-17]。胡永明、康崇等人开展了光纤矢量水听器制作及应用等方面的研究[18-19]。阵列优化设计和阵列信号处理系统仿真中, 大多需要知道阵列输出噪声的相关性, 即阵列输出的噪声协方差矩阵。本文分析了各向同性噪声场中矢量水听器输出的噪声相关性, 给出了描述噪声相关性的一般表达式。并结合概率分析理论, 提出了一种数值仿真噪声的简单方法。通过数值仿真结果与理论值的比较, 证实了文中所给方法的有效性。

1 矢量水听器相关性分析

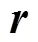
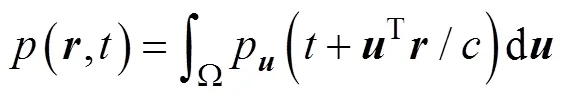
根据欧拉方程[6], 可写出接收点处平面波噪声振速与声压之间的关系为

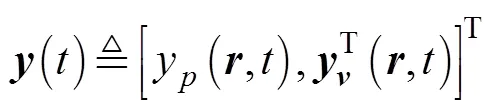
噪声场中两测量点声压和振速的空时互协方差矩阵为

分析海洋环境噪声中声压相关性时大多是将其看作平面波的线性叠加, 且满足如下假定: 1) 从不同方向来的平面波不相关; 2) 所有平面波是广义平稳的。根据上述假定可得不同方向平面波的互协方差矩阵

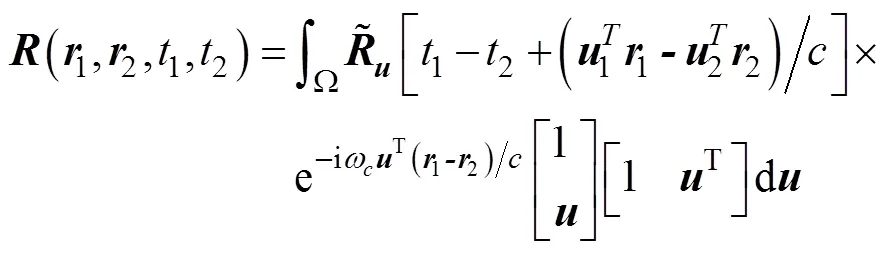
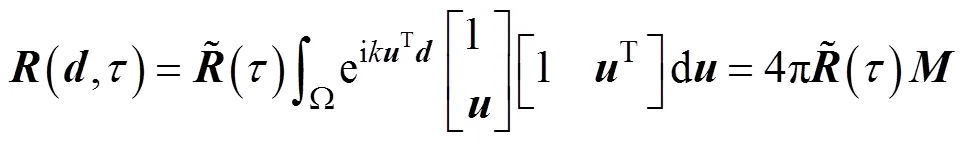
由上式可看出, 声压与振速分量之间相关性为虚数。声压之间的相关性仅与两测量点的距离有关, 而声压与振速之间以及振速之间的相关性还与两测量点之间的相对位置有关。

2 噪声场数值仿真方法

实际仿真过程中, 只能采用有限个在球面上均匀分布的若点声源的共同作用来逼近实际的各向同性噪声场。即各向同性噪声场中矢量水听器的输出可表示为

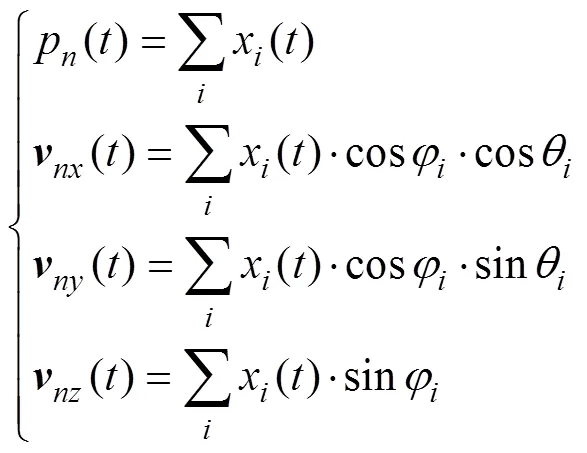
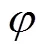
Fig . 1 Schematic of probability analysis of pitch angle

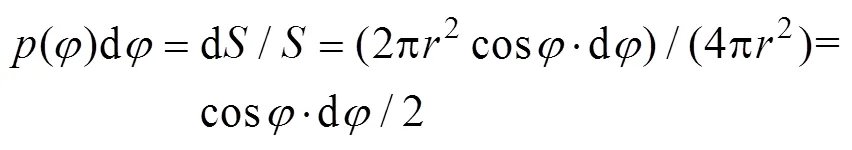
因此可得到俯仰角的概率密度函数

根据图2所示, 同理可得方位角的几何概率

且方位角的概率密度

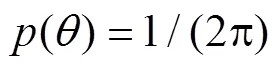
根据式(15)可求得俯仰角的概率积分为

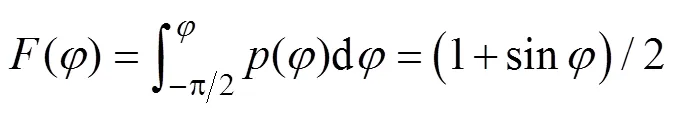
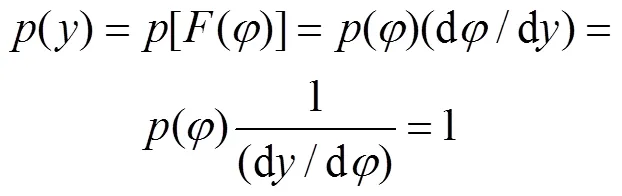
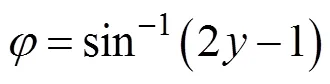
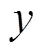
3 数值仿真试验

图3 x轴上阵元间相关曲线图

图3(b)中的曲线相对毛糙, 这是因为仿真过程中所取的点声源的数量和声源的数据点数有限造成的。相当于用3600点的离散求和代替了球面积分, 用1024点数据长度代替了时间平均。如果增加声源的数量, 加大声源的数据点数, 仿真出的噪声相关曲线会更接近理论曲线。

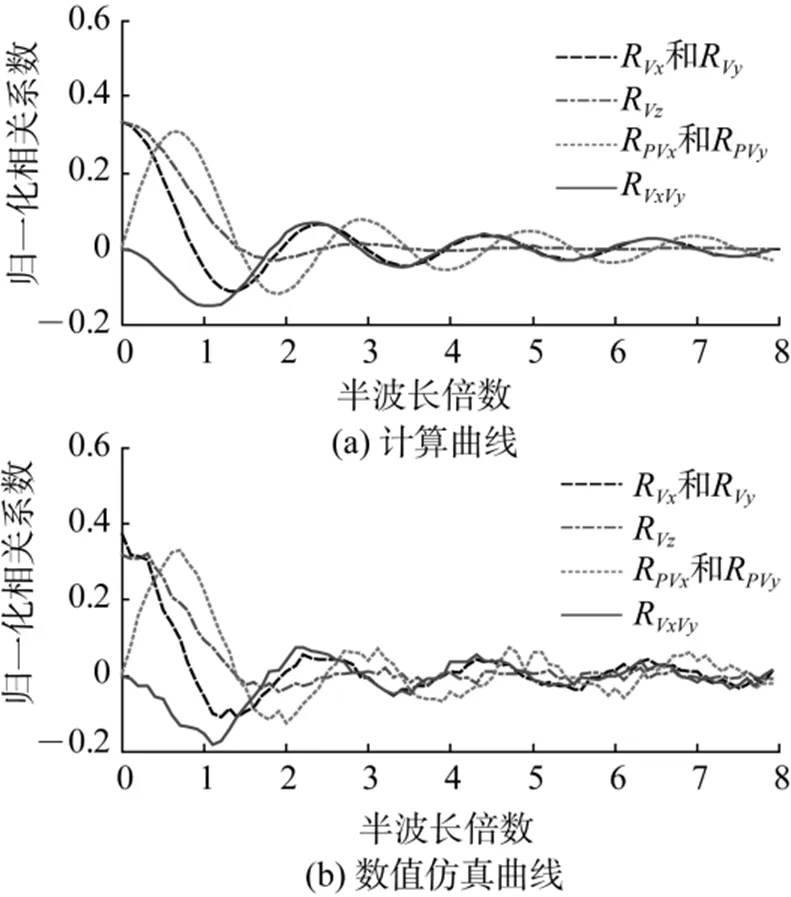
图4 水平面坐标轴对角线上矢量水听器的相关曲线

图5给出了轴上不同阵元间距的相关曲线。其与图3类似, 只是每条曲线所代表的实际物理意义不同, 详细信息在图中标出。比较上下两图可知, 数值仿真的相关曲线与理论值吻合良好。

图5 z轴上矢量水听器的相关曲线图

Fig 5 Correlation curves of two array elementsalong-axis

4 结束语

本文分析了各向同性噪声场中矢量水听器输出间的相关性, 得出了相关性的一般表达式。利用概率分析方法, 总结出各向同性噪声场数值仿真过程中点声源方位角和俯仰角的分布规律, 给出了一种便捷的产生俯仰角序列的方法。数值仿真结果表明, 文中所给方法仿真的矢量水听器在不同位置的相关曲线与理论结果吻合良好。为矢量水听器阵列的优化设计和矢量阵列信号处理系统的仿真分析提供了准确的数值噪声。

[1] 孙贵青, 李启虎. 新型光纤水听器和矢量水听器[J]. 物理, 2006, 35(8): 645-653.

Sun Gui-qing, Li Qi-hu. A Novel Fiber Optic Hydrophone and Vector Hydrophone[J]. Physics, 2006, 35(8): 645-653.

[2] 贾志富. 全面感知水声信息的新传感器技术——矢量水听器及其应用[J]. 物理, 2009, 38(3): 157-168.

Jia Zhi-fu. Novel Sensor Technology for Comprehensive Un- derwater Acoustic Information—Vector Hydrophones and Their Applications[J]. Physics, 2009, 38(3): 157-168.

[3] Berliner M, Lindberg J. Acoustic Particle Velocity Sensors: Design, Performance, and Applications[J].Journal of the Acoustical Society of America, 1996, 100(6): 3478-3479.

[4] Wong K T, Zoltowski D. Closed-form Underwater Acoustic Direction-finding with Arbitrarily Spaced Vector Hydroph-ones at Unknownlocations[J]. IEEE Journal of Oceanic Engineering, 1997, 22(3): 566-575.

[5] MalcolmHawhes. Issues in Acoustic Vector-sensor Proce- ssing[D]. New haven: Yale University, 2000.

[6] Malcolm H, Arye N. Acoustic Vector-Sensor Correlations in Ambient Noise[J]. IEEE Journal of Oceanic Engin- eering, 2001, 26(3): 337-347.

[7] Benjamin A C, Albert H N. Directivity Factor for Linear Arrays of Velocity Sensors[J]. Journal of the Acoustical Society of America, 2003, 113(3): 324-331.

[8] Lars B. Particle Motion Vector Measurement in a Towed, Marine Seismic Cable: USA, 0195648 A1[P], 2007.

[9] Robert E. Rouquette. Towed Streamer Deghosting: USA, 7167413B1[P], 2007.

[10] Henry Cox, Hung Lai. Performance of Line Arrays of Vector and Higher Order Sensors[C]//Signals, Systems and Computers, 2007: 1231-1236.

[11] Hung L, Kristine B. Cramer-Rao Lower Bound for DOA Estimation Using Vector and Higher-Order Sensor Arra- ys[C]//Signals, Systems and Computers, 2007: 1262-1266.

[12] Hung L. Optimum and Adaptive Processing of Acoustic Vector and Higher-order Sensors[D]. George Mason Uni- versity, 2008.

[13] 贾志富. 三维同振球型矢量水听器的特性及其结构设计[J]. 应用声学, 2001, 20(04): 15-20.

Jia Zhi-fu. Design and Characteristics of a Reasonant- sphere Type Three-dimensional Vector Hydrophone[J]. Applied Acoustics, 2001, 15(4): 15-20.

[14] 贾志富. 测量超声场声强用组合式水听器的设计方案[J]. 声学技术, 2001, 20(2): 90-94.

Jia Zhi-fu. Design Schemes of Combined Hydrophones Used for Acoustic Intensity Mesurements of Ultrasonic Field[J]. Technical Acoustics, 2001, 20(2): 90-94.

[15] 惠俊英, 刘宏, 余华兵, 等. 声压振速联合信息处理及其物理基础初探[J]. 声学学报, 2000, 25(4): 303-307.

Hui Jun-ying, Liu Hong, Yu hua-bing, et al. Study on the Physical Basis of Pressure and Particle Velocity Com- bined Processing[J].Chinese Journal of Acoustics, 2000, 25(4): 303-307.

[16] 杨德森, 洪连进. 矢量水听器原理及应用引论[M]. 北京: 科学出版社, 2009.

[17] 杨秀庭, 孙贵青, 李敏, 等. 矢量拖曳式线列阵声纳流噪声影响初探[J]. 声学技术, 2007, 26(5): 775-780.

Yang Xiu-ting, Sun Gui-qing, Li Min, et al. Primary Inve- stigations of the Flow-induced Noise in the Application of Vector Hydrophone Towed Linear Array[J]. Technical Ac- oustics, 2007, 26(5): 775-780.

[18] 康崇, 刘佳杰, 黄宗军. F-P型同振式光纤矢量水听器相位产生载波解调算法[J]. 电子激光, 2011, 22(1): 51-55.

Kang Chong, Liu Jia-jie, Huang Zong-jun. Phase Gene- rated Carrier Demodulation Algorithm for F-P Optical Fiber Vector Hydrophone Array[J]. Journal of Optoele- ctronics Lase, 2011, 22(1): 51-55.

[19] 吴艳群. 拖线阵用光纤矢量水听器关键技术研究[D]. 长沙: 国防科技大学, 2011.

Numerical Simulation Method of Correlation Noise for Vector Hydrophone

WANG Xu-hu1,2, CHEN Jian-feng1, AN Qin-li1

(1. School of Marine Science and Technology, Northwestern Ploytechnical University, Xi′an 710072, China; 2. School of Physics and Engineering, Qufu Normal University, Qufu 273165, China )

The covariance matrix of vector hydrophone array output noise is necessary in the array′s design, performance analysis, and simulation of signal processing system. We analyze the output correlation of the vector hydrophone in isotropic noise field and obtain the general formulas for auto-and cross-correlation between two vector hydrophones. With analysis of the probability, a simple method for numerically simulating isotropic noise field is proposed. Numerical simulation results coincide with the theoretical ones, which indicates the proposed method is effective and can generate accurate numerical noise for optimization design of vector hydrophone array and simulation analysis of its signal pro- cessing system.

vector hydrophone; isotropic noise; correlation; numerical simulation

TJ630.34; TB566

A

1673-1948(2013)05-0342-05

2012-11-25;

2013-01-12.

国家自然基金(61001153); 山东省高等学校科技计划(J09lg07).

王绪虎(1979-), 男, 在读博士, 讲师, 主要从事信号与信息处理、阵列信号处理等方面的研究工作.

(责任编辑: 杨力军)