水声对抗子弹入水冲击响应仿真
2013-05-28邦志辉刘荣忠
邦志辉, 刘荣忠, 郭 锐, 张 俊
水声对抗子弹入水冲击响应仿真
邦志辉, 刘荣忠, 郭 锐, 张 俊
(南京理工大学 智能弹药技术国防重点学科实验室, 江苏 南京, 210094)
水声对抗子弹的入水冲击对其可靠性具有较大影响。采用任意拉格朗日-欧拉(ALE)算法建立了子弹入水冲击动力学仿真模型, 利用球形子弹入水的试验结果验证了仿真的可行性, 进而在不同情况下对子弹入水进行仿真, 并分析了由冲击所引起的空泡现象、运动规律及壳体冲击响应。仿真结果表明, 子弹外形对空泡现象影响较显著; 在子弹入水初期的速度表现出很强的衰减特性; 随着入水角度的增大, 子弹入水稳定性增强, 但轴向冲击阻力增大; 塑料壳体较铝合金壳体对子弹入水冲击的缓冲作用大。
水声对抗子弹; 入水; ALE算法; 空泡; 冲击响应
0 引言
水声对抗弹药作为一种新型反鱼雷软杀伤武器, 已成为舰艇和潜艇等防御鱼雷重要的水中武器[1]。该弹药采用子母弹形式, 由火箭助推器将母弹发射到指定海域上空后, 将水声对抗子弹抛出, 子弹群以一定初速和角度落入水中并形成连续爆炸, 产生混响干扰信号, 诱骗干扰来袭鱼雷。在入水阶段, 子弹将承受强烈的冲击载荷, 可导致弹体结构变形及内部器件损坏, 失去反鱼雷的功效, 进而丧失对舰艇或潜艇的最佳防护时机。因此, 子弹入水冲击是该类型水声对抗弹药研制亟待解决的问题。
结构入水冲击涉及固、液和气三态相互耦合作用的非线性问题, 虽然经历时间短暂(微秒级), 但结构承受了强烈的冲击过载并伴随气垫效应和空泡现象等复杂的物理过程, 广泛存在于实际工程中, 如空投鱼雷入水、水上飞机降落及舰艏砰击等。由于结构入水冲击问题的广泛性和重要性, 国内外学者对其进行了大量研究。在理论方面, Von Kaman提出的附加质量法为理论研究结构入水奠定了基础[2]; Scolan等提出比切片法, 利用逆Wagner理论分析了3D钝体入水冲击问题[3]。在试验方面, Watanabe最早对圆锥体结构入水冲击进行了试验研究, 并测出冲击载荷的时域响应[4]; 顾建农等利用试验研究了旋转弹丸入水, 分析了不同弹丸入水冲击空泡特性及速度衰减规律[5]。由于结构入水冲击涉及到流固间接触面不确定性、冲击瞬时性及气垫效应空泡现象等, 这些因素将成为解析法和试验测试法在实际研究分析过程中的难点。目前, 随着计算机技术的发展, 以有限元法数值仿真结构入水冲击问题得到了广泛应用, 尤其是基于任意拉格朗日-欧拉(Arbitrary Lagrange-Euler, ALE)流固耦合方法解决结构入水冲击问题[6-7], 由于该方法不受结构几何外形、边界条件及气垫效应等限制, 被国内外学者普遍认为是一种分析结构入水冲击问题的有效算法[8]。
本文采用有限元软件LS-DYNA的ALE算法对子弹入水冲击过程进行了数值仿真, 分析了子弹入水冲击现象及不同入水情况的非线性动态响应, 研究结果可为其结构优化设计及强度可靠性评估提供一定的参考。
1 ALE流固耦合算法
非静止的不可压缩Navier-Stocks流体力学控制方程可描述为

边界条件和初始条件分别为


ALE算法除Lagrange和Euler坐标外, 还引入任意参照坐标, 参照坐标相关材料微商描述为
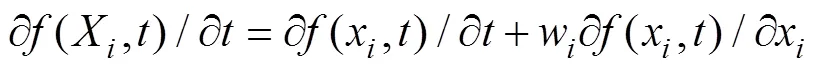
式中:X为拉格朗日坐标;x为欧拉坐标;w为相对速度。利用材料时间导数和参照几何构型时间导数间的替换关系可导出ALE方程。
设为物质速度,为网格速度, 令=-,可得出ALE算法的控制方程为
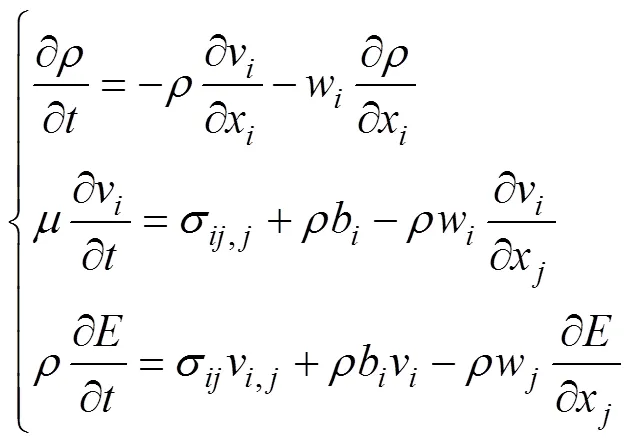
式中:为流体密度;为流体运动黏性系数;b为流体节点质量力;σ为应力张量。
ALE求解过程中的平衡方程为
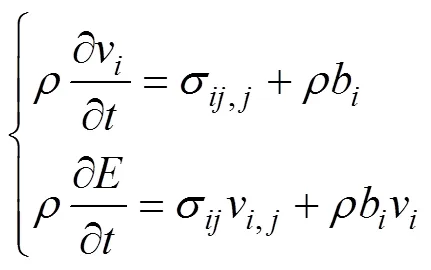
采用罚函数约束法来实现流固耦合, 该方法通过罚函数耦合系数追踪Lagrange从节点和Euler流体主物质位置间的相对位移, 检查每个从节点到主物质表面的贯穿情况, 如果不贯穿, 不做处理; 如果发生贯穿, 界面力则会分布到欧拉流体节点上。大小与贯穿数量成正比, 即

式中:k为基于主从节点质量模型特征刚度系数。
2 子弹入水冲击仿真计算模型
2.1 有限元模型
对抗子弹由壳体和内部炸药组成, 炸药密度=1.787 g/cm3, 2种壳体厚度为2.8 mm, 材料主要参数见表1, 其中, 铝合金采用Johnson-Cook材料模型描述, 工程塑料用Plastic-Kinematic描述, 流体采用Null空材料模型, 其中Null与Johnson- Cook 材料模型结合Gruneisen状态方程描述。该状态方程可通过2种方法定义压力与体积的关系, 来确定材料是压缩还是扩张, 对于空气和水均为压缩材料, 定义如下
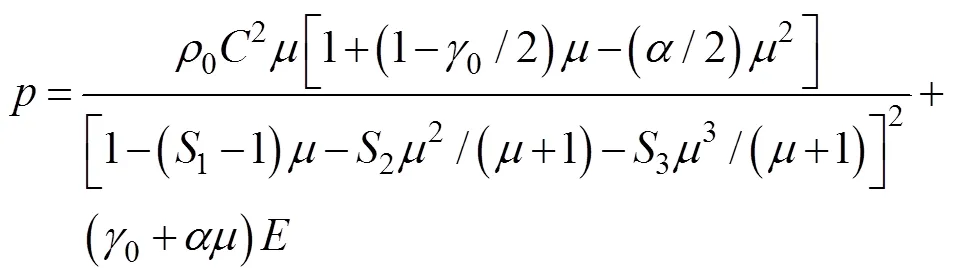
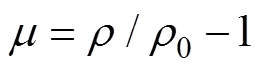
式中:是v-v曲线截距;1,2,3是v-v曲线的斜率系数;0是Gruneisen常数;0和分别是初始和当前密度;和是0的1阶体积修正量,是单位质量内能。空气与水参数见表2。

表1 子弹体材料参数

表2 空气和水相关参数
对各物质进行结构化网格划分, 子弹划分为Lagrange网格单元, 空气和水划分为ALE网格单元。文献[9]对不同Euler与Lagrange网格尺寸比进行了计算, 分析了值与数据收敛的关系, 综合模型尺寸、计算时间及数据收敛等方面因素设为3∶2。子弹及子弹垂直入水有限元模型如图1所示。子弹壳体与炸药采用面面接触; 空气与水域边界采用非反射边界条件; 关键字*ALE_MULTI-MATERIAL_GOUP用于定义多流体单元, *CONSTAINED_LAGRANGE_ IN_SOL将Lagrange描述的固体ID号设为从属单元, 将ALE描述的流体组作为主单元, 通过罚函数法实现固体与流体间的耦合算法, 模型单位制为cm-g-μs。
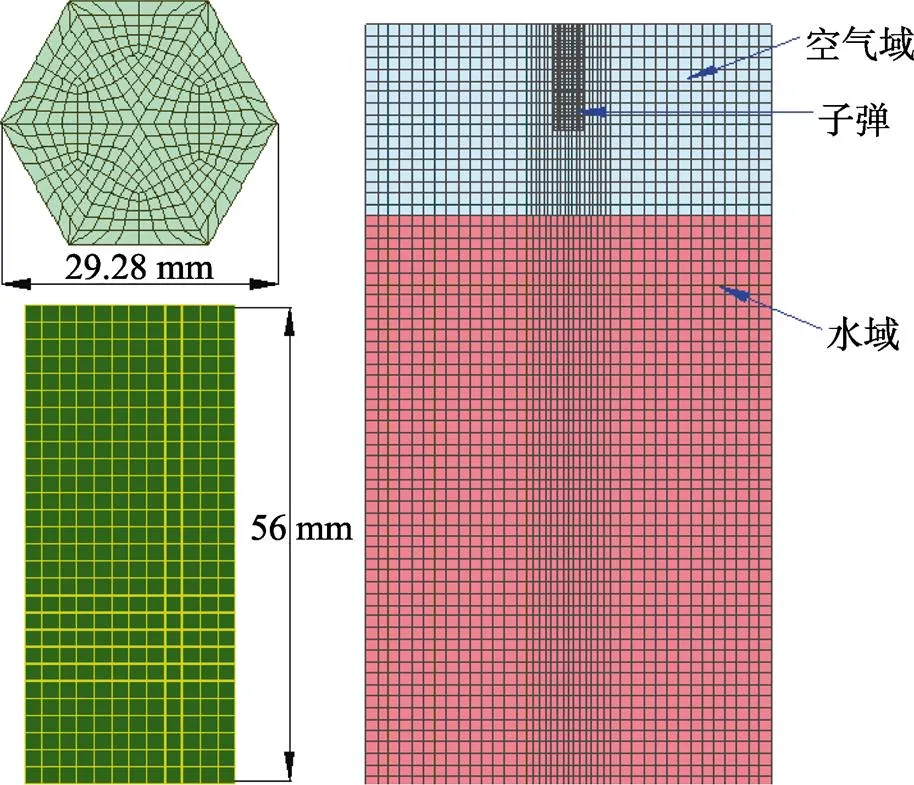
图1 子弹外形及垂直入水冲击模型
2.2 仿真计算试验验证
为了验证数值仿真结构入水冲击的可行性, 选取文献[10]与[11]提供的球形弹丸入水试验数据, 建立有限元模型并进行数值仿真, 分别对比了弹丸入水现象及速度衰减规律, 如图2和图3所示。从图2可知, 弹丸垂直入水仿真出现了与文献[11]试验相同的水面飞溅、隆起及抛物面形空腔等现象, 文献[12]通过对弹丸垂直入水试验研究, 证实了弹丸入水初期空腔为精确的抛物面形。图3表明, 数值求解的入水速度衰减规律与文献[10]提供的试验数据大致相同, 最大相对误差不超过10%。从以上对比分析表明, 采用ALE算法数值仿真子弹入水冲击具有较高的可信度。

图2 试验与仿真对比图
Fig. 2 Comparison of test and simulation
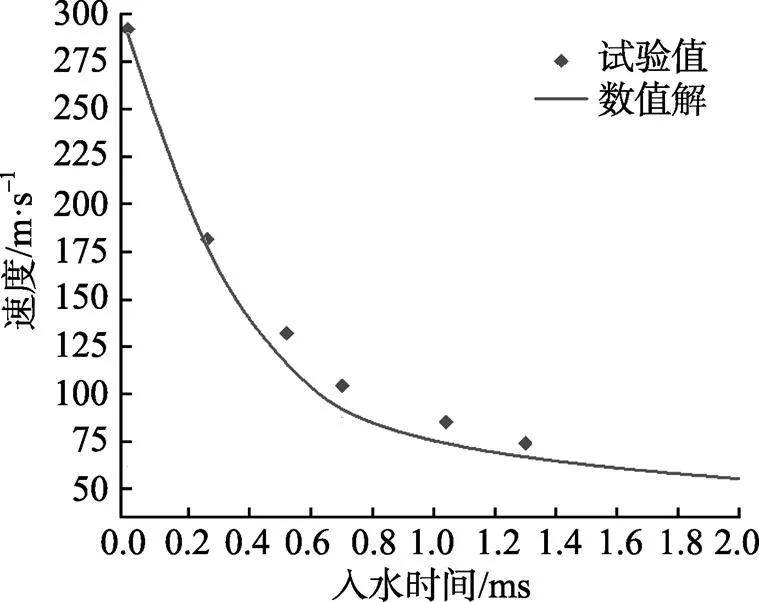
图3 入水速度衰减对比
3 计算结果与分析
3.1 子弹入水现象分析
图4和图5分别为子弹以200 m/s的速度垂直入水时的流体速度和密度云图。由图4可知, 子弹在撞水的瞬间, 与弹体接触的流体大面积迅速向周围扩散, 随着入水时间增加, 子弹运动逐渐趋于稳定, 子弹头部周围流体流速较大并形成“射流”, 而尾部流速降低, 子弹逐渐处于闭合的空腔内。由图5可知, 子弹入水初期水面形成与空气相通的敞开空腔, 由于子弹为平头弹, 空腔形状不像图3中球形弹丸形成具有抛物面形, 而是形如“盆型”, 随着入水时间的增加, 敞开空腔逐渐收缩闭合, 伴随子弹运动逐渐产生包裹整个弹体的卵形空泡, 这是由于高速子弹在水中运动产生伯努利效应, 即附在弹体表面的流体流速增加, 而压力降低, 当将至流体饱和蒸汽压时, 而空泡数又足够少时, 将形成包裹整个弹体的超空泡。子弹入水经历初期的开空腔、空腔闭合、空腔颈缩和后期的超空泡等现象。空腔(泡)的形成与溃灭对子弹冲击过载及运动稳定性有重要的影响, 因此, 子弹入水现象的分析对其结构设计及可靠性评估有重要意义。

图4 不同时刻流体速度云图
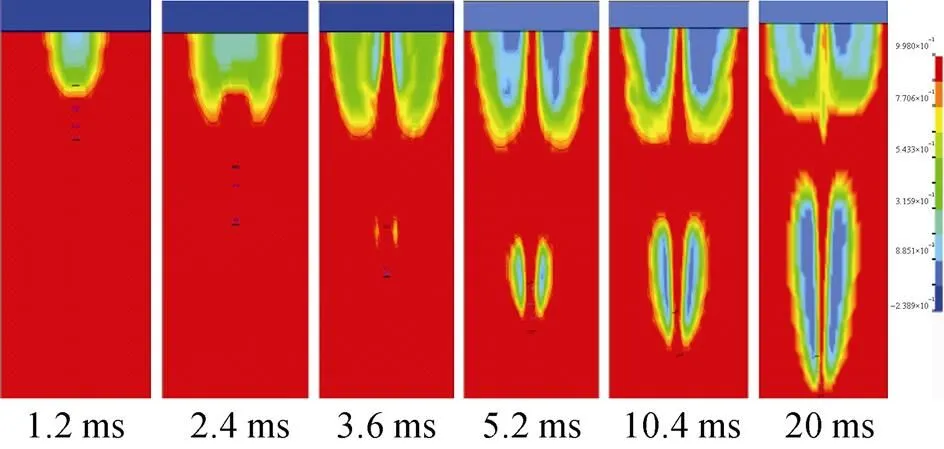
图5 不同时刻流体密度云图
3.2 子弹入水条件分析
考虑到子弹实际入水条件、稳定性与操纵性, 本文对子弹以=20~200 m/s和=30~90o(无攻角)范围内工况进行了数值计算。首先对铝合金壳体子弹垂直(=90o)入水, 速度以20 m/s, 60 m/s, 100 m/s和140 m/s条件下的冲击载荷进行分析, 如图6所示。由于本文所建不同速度子弹模型距水面等高, 故子弹速度越小, 冲击越滞后, 从图6得出, 子弹在入水初期, 冲击载荷迅速增大后逐渐降低, 并保持波动, 最后趋于稳定, 子弹入水速度越大, 冲击载荷峰值越高, 并且入水后达到的峰值时间越短, 但是入水速度越高对子弹壳体强度和内部设备耐冲击性能也要求越高。因此, 实际子弹在入水前进行适当的减速是很必要的。

图6 不同速度时的入水冲击载荷
图7为子弹以=200 m/s,=30o入水时壳体Mises应力云图, 从图中可看出, 壳体最先撞水部位壳底边缘部应力较大, 且该处出现了塑形变形。为了分析冲击过载分布, 依次选取子弹最先入水端的壳底中心到壳体侧面部位, 如图8所示, 从冲击过载峰值最大的壳底边缘处逐渐向周围递减, 由于子弹为平头型, 高速入水时在其头部中心处形成空腔, 而流体对弹体头部边缘处形成冲击, 造成壳头中心部位的冲击过载最小, 而边缘位置处冲击过载最大, 当子弹以小角度高速入水, 不仅会使壳体结构局部强度失效, 而且导致弹体径向载荷增大, 子弹容易出现跳水或忽扑等现象。图9为子弹以入水速度=80 m/s, 角度=30o, 45o, 60o, 75o及90o不同条件下的速度衰减规律曲线, 由图9可知, 子弹在入水初期(0~1 ms), 由于冲击阻力不稳定, 导致不同情况下的速度波动较大, 且速度衰减速率较大, 到后期子弹运动逐渐趋于稳定, 衰减速率也不断降低; 随着入水角度的增大, 速度衰减率增大, 这是因为子弹入水角度越大, 子弹轴向阻力增大, 而入水初速是沿弹轴方向, 因此子弹在水中的速度衰减率变快。子弹以初速=80 m/s, 120 m/s, 160 m/s, 200 m/s垂直入水时速度衰减与时间的规律见图10, 可以看出, 不同入水速度下的子弹都表现出了极强的速度衰减特性, 并且初始入水速度越大, 在水中衰减幅度越大, 从图6显示, 子弹冲击载荷峰值出现在入水初期(0~1.5 ms)内, 在该时段内使得子弹入水阻力增加, 故速度衰减速率最大, 随后, 子弹阻力减小, 运动逐渐稳定, 各速度均以缓慢速率衰减, 文献[12]得出了同样的结论。
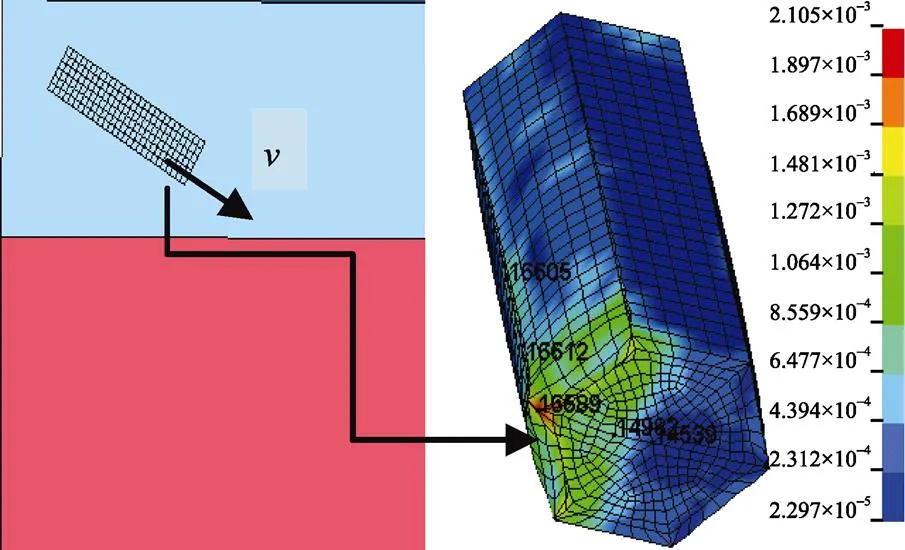
图7 子弹壳体Mises应力云图
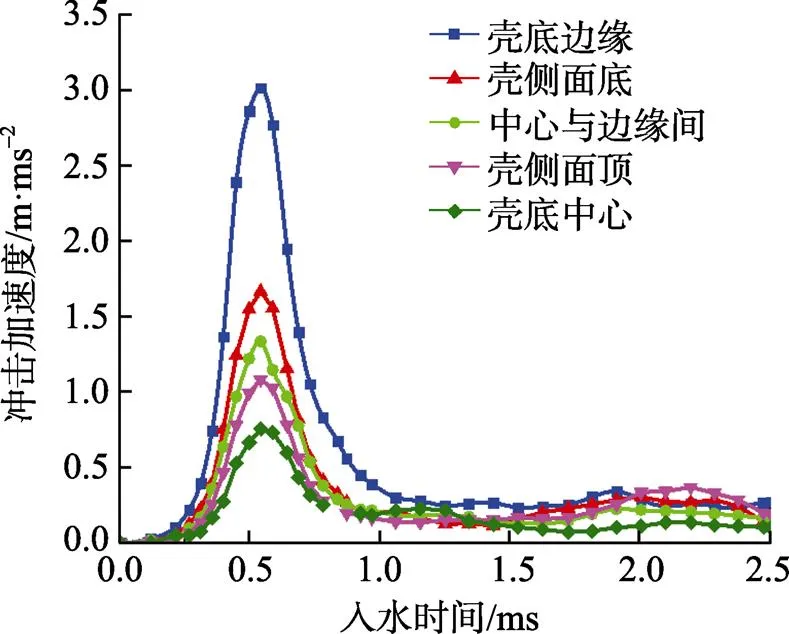
图8 壳体不同位置冲击过载
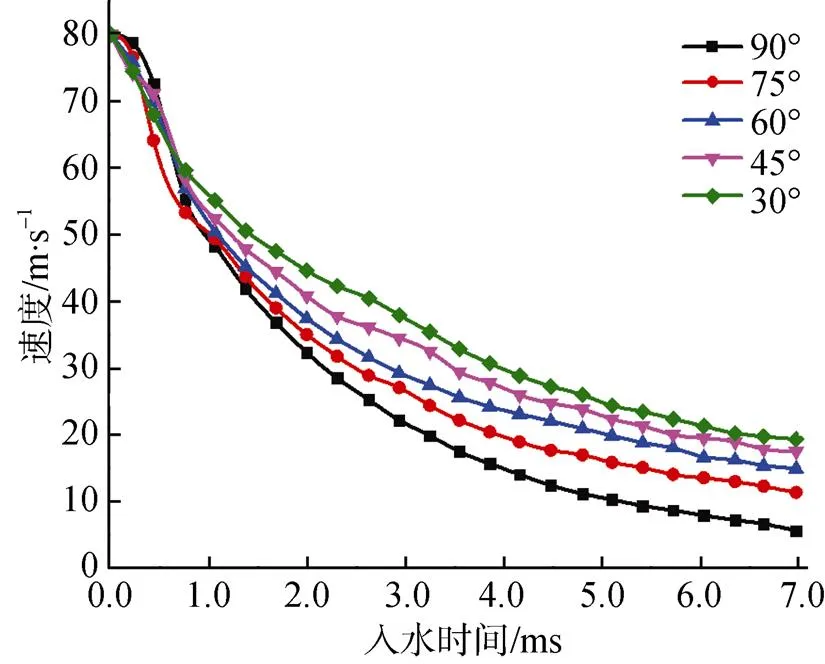
图9 不同入水角度的速度衰减规律
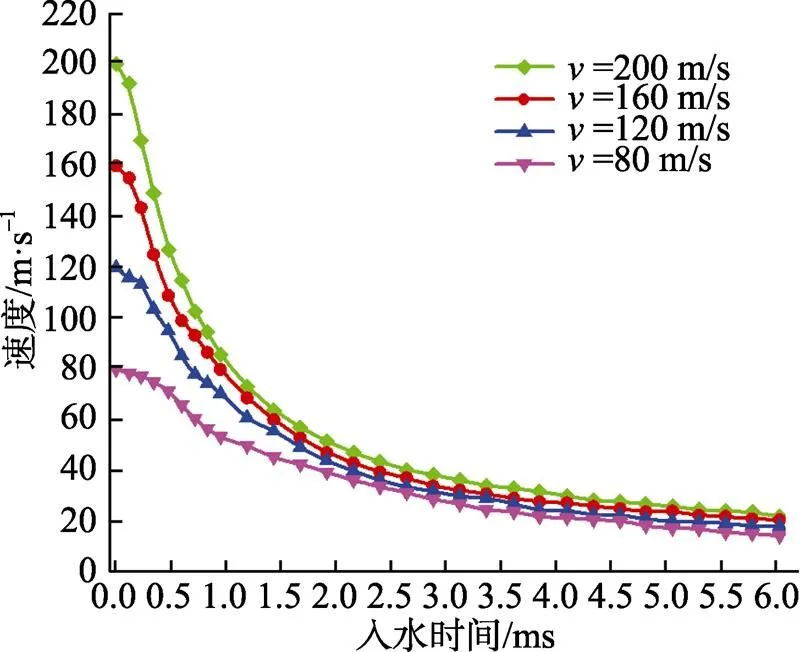
图10 不同入水初始速度的速度衰减规律
3.3 子弹壳体冲击响应分析
子弹壳体对内部器件有重要防护作用, 当子弹高速入水时, 壳体承受强烈的冲击载荷, 尤其在入水初期, 空泡的形成和溃灭会对壳体产生强烈的脉冲载荷和扰动。本文对铝合金和工程塑料2种壳体材料的子弹入水冲击响应进行了分析, 如图11和图12分别为子弹垂直入水时不同速度下的冲击载荷峰值和冲击应力峰值变化规律。图11显示, 2种材料壳体的冲击载荷峰值均随速度增加呈递增趋势, 在相同速度下, 铝合金比塑料壳体载荷峰值要大, 主要是因为塑料弹性模量小, 对冲击有一定的缓冲作用。从图12看出, 塑料壳体应力峰值随入水速度增加几乎呈线性递增; 铝合金壳体在40~70 m/s范围内增速较大, 工程塑料的极限屈服强度约为310 MPa, 当速度继续增加, 塑料壳体将会出现塑形变形。因此, 子弹以高速入水时, 需对其设计缓冲或减速装置, 以减小子弹入水时壳体所受的冲击载荷。
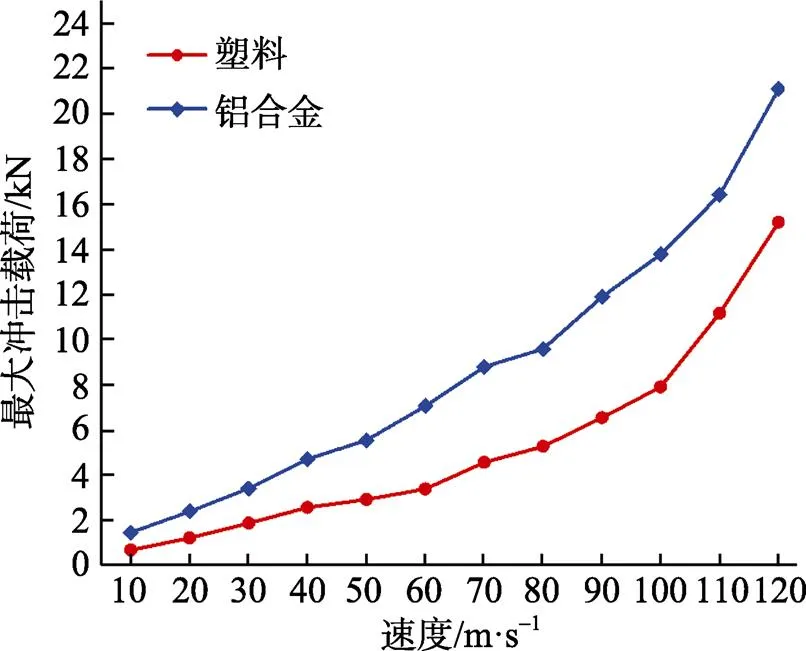
图11 不同入水速度的2种壳体冲击载荷峰值

图12 不同入水速度的2种壳体应力峰值
4 结论
基于LS-DYNA的ALE算法对球形子弹入水进行仿真, 所得相关结果与文献[10]、[11]所做试验吻合较好, 进而验证了该方法模拟水声对抗子弹入水冲击的可行性, 得出以下结论。
1) 给出了子弹入水时流体速度和密度变化, 分析了子弹入水空泡产生过程, 得出空泡的形成与溃灭会对弹体产生强烈的脉冲载荷和动态扰动。
2) 子弹以20~140 m/s垂直入水时, 速度越大, 冲击载荷峰值越大, 到达峰值的时间越短, 20 m/s与140 m/s入水冲击载荷峰值相差12.3 kN, 前者到达峰值需1.76 ms, 而后者仅需0.59 ms。
3) 子弹以一定角度斜入水时, 弹体最先撞水部位出现强烈的冲击过载, 并逐渐向周围递减, 最大值达2.8×106m/s2。随着入水角度的增加, 轴向阻力逐渐增大, 入水速度衰减速率升高; 在入水初期, 子弹速度表现出很强的衰减特性, 随着入水时间的增加, 运动趋于稳定, 速度衰减变缓, 且入水初速越大, 衰减越快。
4) 相比铝合金壳体, 塑料壳体对弹体入水具有一定缓冲作用, 冲击载荷峰值随子弹入水速度的增加呈非线性, 而应力峰值几乎显现线性增加, 入水速度对铝合金壳体冲击强度影响较大。
[1] 潘正伟, 焦善武, 顾晓辉. 水下爆炸——高功率宽频带的水声干扰源[J]. 南京理工学报, 1999, 23(6): 507-509.Pan Zheng-wei, Jiao Shan-wu, Gu Xiao-hui. Underwater Explosion is an Acoustic Interference Source with High Power and Wide Band[J]. Journal of Nanjing University of Science and Technology, 1999, 23(6): 507-509.
[2] Von Kaman. The Impact of Seaplane Floats During Landing[R]. NACA Technical Notes 321, 1929.
[3] Scolan Y M, Korobkin A A. Energy Distribution from Vertical Impact of a Three-dimensional Solid Body onto the Flat Surface of an Ideal Fluid[J]. Journal of Fluids and Structures, 2003, 17(2): 275-286.
[4] Watanabe S. Resistance of Impact on Water Surface, Part V-Sphere[J]. Scientific Papers of the Institute of Physical and Chemical Research of Japan, 1934, 23(484): 202-208.
[5] 顾建农, 张志宏, 王冲, 等. 旋转弹头水平入水空泡及弹道的实验研究[J]. 兵工学报, 2012, 33(5): 540-544.Gu Jian-nong, Zhang Zhi-hong, Wang Chong, et al. Experimental Research for Cavity and Ballistics of a Rotating Bullet Entraining Water Levelly[J]. Acta Armamentarii, 2012, 33(5): 540-544.
[6] 郑金伟, 宗智. 2D刚体椭圆头结构高速撞水模拟[J]. 鱼雷技术, 2008, 16(2): 9-12.Zheng Jin-Wei, Zong Zhi. Simulation of Two-dimensional Rigid Elliptic Head Structure Water Entry at High Speed [J]. Torpedo Technology, 2008, 16(2): 9-12.
[7] 陈福. 结构入水问题的流固耦合仿真[D]. 北京: 清华大学, 2008.
[8] 张阿漫, 戴绍仕. 流固耦合动力学[M]. 北京: 国防工业大学出版社, 2011.
[9] 魏照宇, 石秀华. 回转体高速垂直入水冲击特性研究[J]. 鱼雷技术, 2010, 18(5): 339-342.Wei Zhao-yu, Shi Xiu-hua. Research on Impact Characteristics of High Speed Vertical Water Entry of an Axisymmetric Body[J]. Torpedo Technology, 2010, 18(5): 339-342.
[10] 乔相信, 阎思江, 万仁毅. 弹丸入水空泡试验和入水道速度计算[J]. 沈阳理工大学学报, 2007, 26(6): 51-54.Qiao Xiang-xin, Yan Si-jiang, Wan Ren-yi. The Vacuole Experiment and Computation of Trajectory Velocity when the Projectile Entering into Water[J]. Transactions of Shenyang Ligong University, 2007, 26(6): 51-54.
[11] Worthington A M. Impact with a Liquid Surface Studied with Aid of Instantaneous Photography[J]. Philosophical Transactions of the Royal Society of London, 1900, 194 (A): 175-199.
[12] 张伟, 郭子涛, 肖新科, 等. 弹体高速入水特性试验研究[J]. 爆炸与冲击, 2011, 31(6): 579-584.Zhang Wei, Guo Zi-tao, Xiao Xin-ke, et al. Experimental Investigations on Behaviors of Projectile High-speed Water Entery[J]. Explosion and Shock Waves, 2011, 31(6): 579-584.
Simulation on Impact Response to Water Entry of Underwater Acoustic Countermeasure Bullets
BANG Zhi-hui, LIU Rong-zhong, GUO Rui, ZHANG Jun
(Ministerial Key Laboratory of ZhiNengDanYao, Nanjing University of Science & Technology, Nanjing 210094, China)
The water entry impact of underwater acoustic countermeasure bullets has a significant influence on the reliability of the bullet. A dynamic simulation model of water entry impact is established by arbitrary Lagrange-Euler(ALE) algorithm. The feasibility of the simulation is verified by an experiment of a spherical bullet entering into water. Furthermore, numerical simulations of water entry impact of underwater acoustic countermeasure bullets are conducted in different conditions to analyze the cavitation, the bullet motion and the shock response of shell, which are caused by the water entry impact of the bullet. The results show that the cavitation is significantly influenced by the shape of bullets; the bullet speed exhibits high attenuation characteristic at the early stage of water entry; with the water entry angle increasing, the stability of bullet entering into water enhances, but the axial impact resistance gets larger; compared to the aluminum shell, buffering effect of the plastic shell on the water entry impact of the bullet is larger.
underwater acoustic countermeasure bullet; water entry; ALE algorithm; cavitation; impact response
TJ415.6; O353.4
A
1673-1948(2013)05-0326-06
2013-05-07;
2013-06-16.
国家自然科学基金——青年科学项目(1102088).
邦志辉(1986-), 男, 在读硕士, 研究方向为水声对抗子母弹结构设计及强度可靠性分析.
(责任编辑: 陈 曦)
