生存分析理论在鱼雷贮存可靠性评估中的应用

谢 勇, 苑秉成, 谢 辉



生存分析理论在鱼雷贮存可靠性评估中的应用

谢 勇1, 苑秉成1, 谢 辉2

(1. 海军工程大学 兵器工程系, 湖北 武汉, 430033; 2. 中国人民解放军91388部队, 广东 湛江, 524022)

在鱼雷贮存失效时间数据具有删失性的情况下, 科学合理地评估鱼雷贮存可靠性具有重要的现实意义。根据鱼雷贮存期间的区间删失数据, 由生存分析理论的turnbull估计与最大似然估计方法, 运用MATLAB软件编制相应的计算程序, 分别对某批次鱼雷的贮存可靠性进行了估计。实例计算表明, 应用生存分析理论能够有效解决贮存失效时间删失条件下鱼雷贮存可靠性评估问题, 并得到更加合理的评估结果。

鱼雷; 贮存可靠性; 生存分析; 最大似然估计; turnbull估计

0 引言

鱼雷是一种能够在水下自动航行、自动控制、自动寻找与跟踪、命中目标时能自动爆炸的攻击性兵器[1-2], 又称为水下导弹。由于鱼雷在水下航行并攻击水下目标或目标的水下部分, 因此具有很好的隐蔽性与强大的爆炸威力, 在历次海上战争中发挥了重大作用, 可以说鱼雷在过去是、现在是、将来也是最重要的水中兵器之一[3]。

鱼雷武器作为一种长期贮存[4], 一次(作为战雷)或有限次[5](作为操雷)使用的武器系统, 从出厂交付部队到报废或退役, 其大部分时间都处于贮存状态[6], 少数时间处于舰艇装载及操雷实航状态。为方便研究, 本文忽略舰艇装载与鱼雷实航对其服役期间的质量影响, 近似认为鱼雷在部队服役期间都处于贮存状态。鱼雷贮存可靠性通常以平均贮存寿命(平均无故障间隔贮存时间)与贮存可靠度来表征。平均贮存寿命是指在规定的条件下, 鱼雷从开始贮存到发生故障的间隔时间, 或连续两次故障间隔时间的平均值[7]。贮存可靠度是指鱼雷从验收合格包装贮存之日起, 在规定的仓库贮存条件下和规定贮存时间内, 保持规定功能的概率[8], 这里所讲的保持规定功能的概率是指雷上整机通过单元测试、鱼雷通过综合测试的合格率[9]。鱼雷平均贮存寿命与贮存可靠度的分析计算结果可以用来: 1) 分析鱼雷武器贮存期间质量随贮存时间的变化规律; 2) 科学制定维修大纲与计划、定检周期、备件标准、贮存条件、延寿时机及延寿工作的深度和广度, 合理确定维修费用[10]。因此, 对鱼雷武器贮存可靠性问题进行研究具有重要而深远的军事意义。

然而鱼雷武器在贮存过程中无法对其实施全面监测, 因此, 为维持鱼雷武器规定的战术性能与指标, 保持较高的战备完好率, 需在贮存期间对鱼雷武器装备进行定期或不定期检测[11]。在周期检测发现鱼雷失效与故障时, 无法得知故障究竟在检测时刻还是在检测前发生, 只能得到故障时间处于相邻的2个检测时间区间内这一信息。在鱼雷每次检测均完好时, 鱼雷确切寿命也确定, 只知道大于最后一次检测时间。因此, 鱼雷贮存失效时间数据具有区间删失性或不精确性的特点, 无法根据经典的可靠性评估方法准确合理地评估鱼雷武器的贮存可靠性。生存分析理论是近二三十年发展起来的数理统计新分支, 主要研究随机删失数据的统计分析[12], 它不但可以用于生物和医学领域, 而且可用于工程科学, 如可靠性工程等。利用生存分析理论评估鱼雷武器贮存可靠性可以有效解决故障时间不确定的问题, 从而得到更加合理的评估结果。

通常根据所分析对象的生存函数类型是否确定, 将生存分析分为非参数方法与最大似然估计方法。本文将根据鱼雷贮存期间历次检测数据, 分别运用非参数方法与最大似然估计方法分析计算鱼雷武器的贮存可靠性。

1 生存分析基本概念

表1 寿命数据类型表

1) 概率密度函数

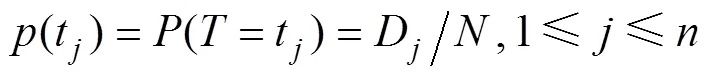
2) 生存函数

3) 危险率函数

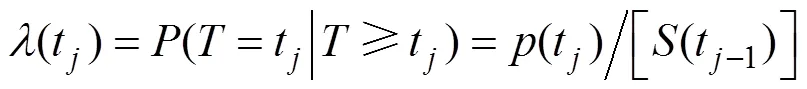
4) 平均寿命

2 鱼雷失效时间数据

鱼雷在贮存期间发生的故障在其检测前无法及时发现与修复, 只有通过检测才能发现。故而鱼雷贮存失效时间数据包括有右删失数据、左删失数据与区间删失数据。为研究方便这里将右删失数据与左删失数据视为广义区间删失数据, 即鱼雷贮存失效时间数据, 其表达式为

3 鱼雷贮存可靠性的Turnbull估计

运用Turnbull方法估计鱼雷贮存可靠度(生存概率)与平均贮存寿命的步骤如下。

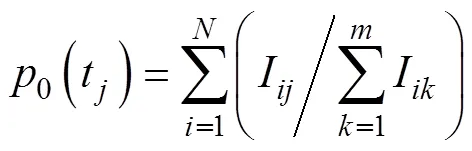
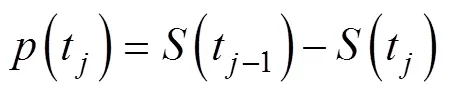
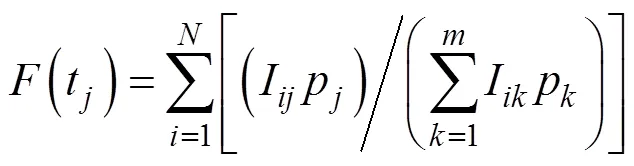
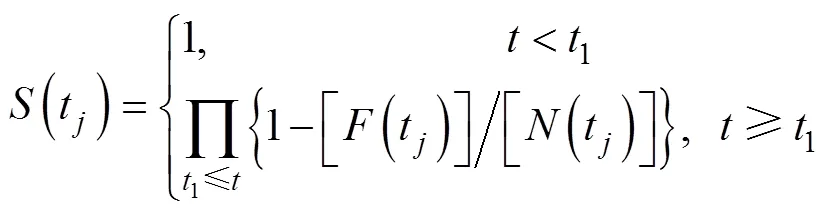
10) 求解平均贮存寿命

4 鱼雷贮存可靠性最大似然估计

最大似然估计是适应面最广的优良估计法, 它是在已知或假定研究对象的寿命分布函数后, 利用观测数据(允许有右删失、左删失和区间删失)进行参数估计。

4.1 鱼雷武器贮存寿命分布函数

对于现代鱼雷武器而言, 尽管其是一个包含电子、机电、机械、橡胶与化工等产品的复杂系统, 但仍可按指数分布模型来分析处理鱼雷贮存可靠性问题, 这在工程上是可行的, 可以得到满意的结果[28]。因此下文将在鱼雷贮存可靠性为指数分布的前提下进行最大似然估计, 则有鱼雷贮存可靠性的分布函数为

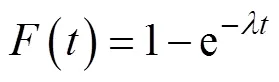
4.2 似然函数

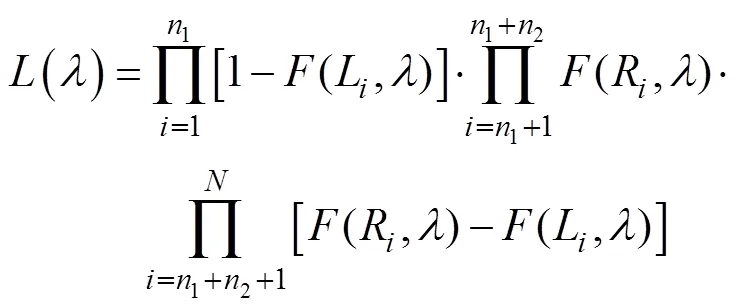
结合式(16), 则有

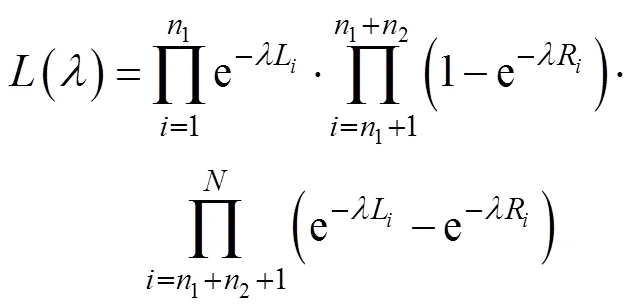
对式(18)两边取对数, 得

5 实例计算

假定装备有39条鱼雷, 假设其贮存失效时间删失数据如表2所示。

1) Turnbull估计方法计算

根据Turnbull估计方法, 应用MATLAB软件编制计算程序, 可得贮存可靠度函数如图1。图1较好地反映了鱼雷贮存可靠度随贮存时间的变化规律, 随着贮存时间的延长, 贮存可靠度下降。

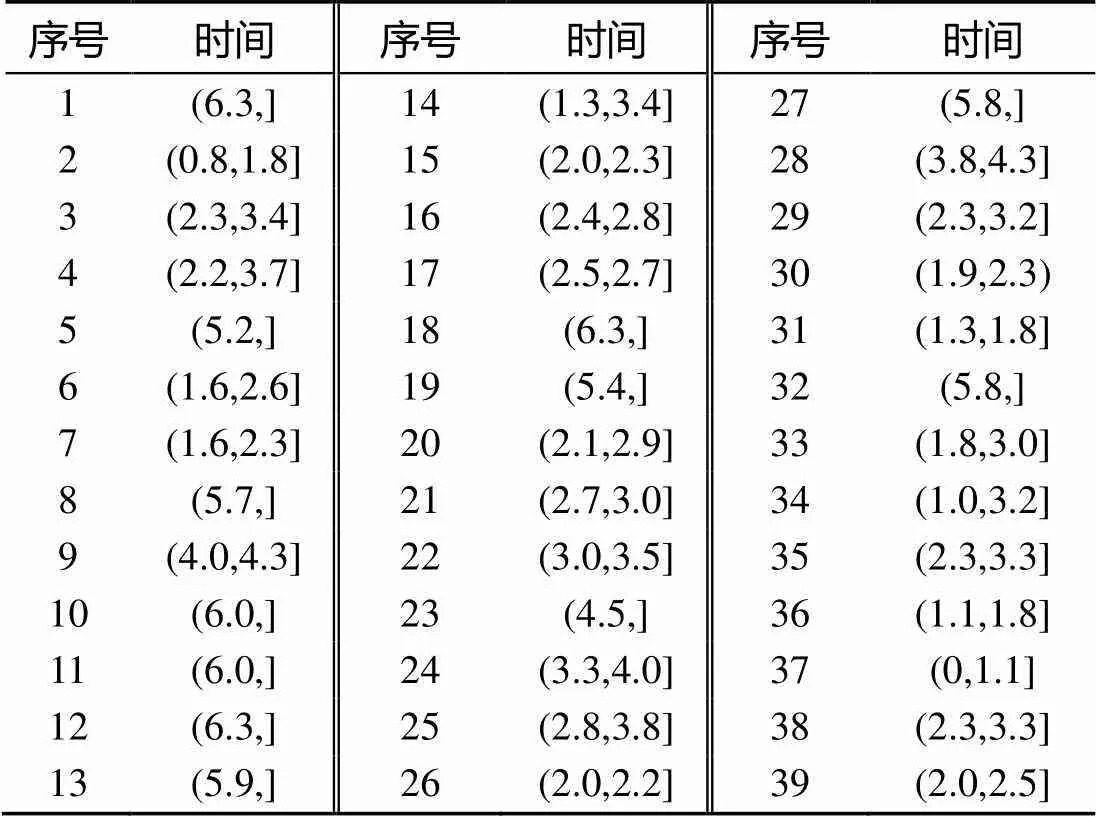
表2 失效时间删失数据表

图1 贮存可靠度变化规律

2) 最大似然估计方法计算

6 结束语

本文针对鱼雷贮存可靠性评估问题, 考虑到鱼雷贮存失效时刻并不一定是鱼雷检测的时刻, 检测数据具有删失性这一特点, 运用生存分析理论计算分析了鱼雷贮存可靠性, 其中turnbull估计方法得出的平均贮存寿命较最大似然估计方法计算的平均无故障时间小, 说明Turnbull估计方法较保守, 而最大似然估计方法较冒进。结果表明, 本文介绍的方法有效实用, 更贴近鱼雷武器实际情况, 能够满足鱼雷武器的工程实际需要, 具有较好的推广价值。

[1] 宋保维. 鱼雷系统工程原理与方法[M]. 哈尔滨: 哈尔滨工业大学出版社, 2010: 15-16.

[2] 石秀华, 王晓娟. 水中兵器概率(鱼雷分册)[M]. 西安: 西北工业大学出版社, 2005: 1-2.

[3] 张宇文. 鱼雷总体设计原理与方法[M]. 西安: 西北工业大学出版社, 1998: 1-2.

[4] 钟强晖, 张志华, 董理. 鱼雷装载可靠度的评估方法[J]. 舰船科学技术, 2010, 32(6): 73-74.Zhong Qiang-hui, Zhang Zhi-hua, Dong Li. The Evaluation Method of Torpedo Loaded Reliability[J]. Ship Science and Technology, 2010, 36(6): 73-74.

[5] 宋保维, 姜军. 鱼雷作战效能分析[J]. 火力与指挥控制, 2007, 32(1): 103-104.Song Bao-wei, Jiang Jun. Analysis of Combat Effectiveness for Torpedo[J]. Fire Control and Command Control, 2007, 32 (12): 103-104.

[6] 任景梅. 鱼雷环境条件及防潮、防霉、防腐蚀方法[J]. 环境技术, 1997(3): 19-20.

[7] GJB531A-96. 鱼雷通用规范[S]. 北京: 国防科技工业委员会, 1996.

[8] 王静. 导弹贮存指标体系研究[J]. 强度与环境, 2012, 39(2): 58-60.Wang Jing. The Research of Storage Indicator System for Missile[J]. Structure& Environment Engineering, 2012, 39 (2): 58-60.

[9] 王万帆. 一种鱼雷贮存可靠性的评估方法[J]. 海军装备, 2009(12): 25-26.

[10] 刘梦军. 现场数据是研究导弹贮存可靠性的基础[J]. 海军海空工程学院学报, 1992, 7(2): 41-44. Liu Meng-jun. Field Data Provide the Basis for Studying Storage Reliability of Missile[J]. Journal of Naval Aerona- utical Engineering Academy, 1992, 7(2): 41-44.

[11] 房俊伟. 基于储存期间的某型鱼雷检测周期预测[J]. 舰船科学技术, 2010, 32(11): 73-76． Fang Jun-wei. Torpedo Inspection Period Forecast Based on Storage Time[J]. Ship Science and Technology, 2010, 32(11): 73-76.

[12] 王启华. 生存数据统计分析[M]. 北京: 科学出版社, 2006.

[13] 陈家鼎. 生存分析与可靠性[M]. 北京: 北京大学出版社, 2005.

[14] 黎子良. 生存分析[M]. 北京: 中国人民大学出版社, 2003: 41- 47.

[15] 彭非, 王伟. 生存分析[M]. 杭州: 浙江科学技术出版社, 1993: 7-11.

[16] 张良霞. 均匀设计在生存资料抽样调查中的应用研究[D].南京: 南京信息工程大学, 2009: 16-20.

[17] 姜英秀. Turnbull估计的计算方法及其比较[D]. 延边: 延边大学, 2007: 2-4.

[18] Turnbull B W. Nonparametric Estimation of a Survivorship Function with Doubly Censored Data[J]. Journal of the American Statistical Association, 1974(69): 169-173

[19] Turnbull B W. The Empirical Distribution Function with Arbitrarily Grouped, Censored and Turncated Data[J]. Journal of the American Statistical Association, 1976(38): 290-295.

[20] 郑为益. 基于生存分析的客户流失模型研究[D]. 广州: 华南理工大学, 2011: 6-10.

[21] Klein J P, Moeschberger M L. Survival Analysis Techniques for Censored and Truncated Data[M]. Springer-Verlag New York, 1997: 135-146.

[22] Zhang Zhi-gang, Sun Jian-guo. Interval Censoring[J]. Statistical Methods in Medical Research, 2010(19): 53-70.

[23] Shen Pao-sheng. The Nonparametric Maximum Likelihood Estimator for Middle-censored Data[J]. Journal of Statistical Planning and Inference, 2011(141): 2494-2499.

[24] Li Lin-xiong, Watkins T, Yu Qi-qing. An EM Algorithm for Smoothing the Self-consistent Estimator of Survival Functions with Interval-censored Data[J]. Board of the Foundation of the Scandinavian Journal of Statistics, 1997(24): 531-537.

[25] 李颖. 自变量为区间删失数据的线性回归分析[D]. 上海:华东师范大学, 2008: 4-8.

[26] Sun Jian-guo. The Statistical Analysis of Interval-censored Failure Time Data[M]. New York: Springer, 2002: 50-50.

[27] 王羿升, 张晋昕, 骆福添. 含有区间删失数据的生存函数估计及其SAS实现[J]. 中国医院统计, 2012, 19(1): 2-3.Wang Yi-sheng, Zhang Jin-xin, Luo Fu-tian. Estimating Survival Functions of Interval-censored Data with SAS[J]. Chinese Journal of Hospital Statistics, 2012, 19(1): 2-3.

[28] 孟庆玉. 鱼雷可靠性工程基础[M]. 武汉:海军工程学院出版社, 1989: 293-295.

[29] 刘金梅, 王建萍, 张力. 生存分析法在弹药贮存可靠性评估中得应用[J]. 弹箭与制导学报, 2004, 24(4): 332-335.Liu Jin-mei, Wang Jian-ping, zhang Li. The Application of Survival Analysis to Evaluation of Ammunition Storage Reliability[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2004, 24(4): 332-335.

[30] 李长福, 夏建中, 黄跃德, 等. 考虑删失数据时弹药贮存可靠性评估方法研究[J]. 兵工学报, 1996, 17(4): 304-306．Li Chang-fu, Xia Jian-zhong, Huang Yue-de, et al. Method of Assessment for the Reliability of Ammunition Storage Considering Censoring of Data[J]. ACTA Armamentarii, 1996, 17(4): 304-306.

[31] 陈家鼎. 生存分析与可靠性引论[M]. 安徽:教育出版社, 1993: 43-48.

Application of Survival Analysis Theory to Reliability Assessment of Torpedo Storage

XIE Yong1, YUAN Bing-cheng1, XIE Hui2

(1. Department of Weaponry Engineering, Naval Engineering University, Wuhan 430033, China; 2. 91388thUnit, The People′s Liberation Army of China, Zhanjiang 524022,China)

In the case of storage failure time data having the censoring characteristic, it is of significance to scientifically and rationally assess torpedo storage reliability. In this study, on the basis of the censored data of torpedo storage time, the storage reliability of the torpedoes in a batch is assessed respectively by using the turnbull estimation method and the maximum likelihood estimation method in survival analysis theory, and the corresponding calculation program is coded by the software MATLAB. Calculation results of an example show that the survival analysis theory is effective for assessment of torpedo storage reliability in the case of storage failure time data censoring, and can obtain more reasonable assessment.

torpedo; storage reliability; survival analysis; maximum likelihood estimation; turnbull estimation

TJ631; TB114.3

A

1673-1948(2013)05-0332-05

2012-12-18;

2013-02-05.

谢 勇(1985-), 男, 在读博士, 研究方向为鱼雷定型与可靠性评估.

(责任编辑: 陈 曦)