考虑机网协调的新型发电机失磁保护方案研究
2013-05-25陆秋瑜张建坤
陆秋瑜,徐 飞,胡 伟,张建坤,李 淼,冯 钢
(1.清华大学电机系电力系统国家重点实验室,北京 100084;2.湖北省电力公司调度通信中心,湖北 武汉 430077;3.内蒙古华电玫瑰营风力发电有限公司,内蒙古 呼和浩特 010000)
0 引言
随着我国“三华”联网工程稳步实施以及华能玉环、上海外高桥三期等一批单机容量1 000 MW的火电机组陆续投入运行,我国电力工业已进入大电网-大机组阶段。在“厂网分开、统一调度”的发展趋势下,加强机网协调,是确保电网和电厂安全稳定运行、构建坚强智能电网的基础。大型发电机涉网保护的优化配置是机网协调的关键技术之一。励磁保护是发电机保护的核心,其中失磁保护因其发生概率高、对机组和系统影响大且整定困难受到了广泛关注[1-2]。近年来国内发生了多起失磁保护误动或拒动的事故[3-4],对机组本身和系统都造成了较大的冲击;在美加8.14 大停电中,因系统振荡造成十多台发电机失磁保护误动跳闸,加剧了电力系统的崩溃[5]。因此,研究性能良好的失磁保护,对保证机组和系统的安全稳定运行具有重要的意义。
为了提高失磁保护的动作速度与可靠性,学者们提出了诸多方法,可以分为改进传统方案和提出新型方法两类。文献[6]提出利用发电机功率变化量作为失磁保护辅助加速判据的方法,但没有考虑到发电机正常运行时可能会出现有功、无功输出同时减小的情形,导致加速判据失效;文献[7]利用PMU数据构建的加速判据在显著提高保护动作速度方面进行了有益探索,但由于失磁发电机定子电势在失磁过程中并不是始终减小,且PMU 数据存在误差,辅助判据在理论和实践上存在缺陷;文献[8]引入模糊机制并舍弃固定延时环节,在增强保护可靠性的同时提高了保护的动作速度,具有一定的理论价值。在新型失磁保护方面,直测功率角[9]、逆无功原理[10]等新型失磁保护方案都较好地利用了失磁发电机的特征信息,但其速动性和可靠性往往不能兼顾。
造成现有失磁保护性能欠佳的主要原因是为了区别失磁和振荡现象,采用了动作时间较长的异步阻抗圆元件及固定延时元件为主判据,导致动作缓慢但可靠性仍不能满意。因此,本文舍弃了传统方案,基于发电机失磁和振荡时不同的电气量变化规律,结合不同失磁类型的特点,提出了电压、无功和时间三种新型判据,进而设计了计及机网协调的新型失磁保护方案,并给出了相应动作参数的整定方法。通过PSASP 仿真分析了新型方案在多种工况及多种故障下动作特性,该方案可有效区分失磁和振荡现象,在提高保护可靠性的同时,可加快保护的动作速度,从而验证了所提方案的有效性。
1 失磁、振荡时的电气量变化
为区分失磁故障与系统振荡现象,将对这两种工况的电压、无功和功角变化规律进行理论推导。
1.1 失磁、振荡时的电压变化规律
1.1.1 同步发电机失磁时的电压变化规律
本文失磁分析基于图1的单机无穷大系统。同步发电机失磁后,转子励磁电流逐渐衰减,发电机很快转入进相状态,从系统吸收无功以建立机组的励磁,造成机端电压和系统电压的降低。

图1 单机无穷大系统Fig.1 A single-machine infinite-bus power system
以发电机短路导致全失磁为例,推导电压的变化规律。设发电机定子绕组的电阻为零,推导可得定子电压幅值的表达式为[11]

其中:Xt、Xs、Xd含义如图1所示;XdΣ为发电机和无穷大系统间的联系电抗;Eq0为失磁前发电机电势;T′d为定子短路情况下励磁绕组的时间常数;s为滑差;f1、f2为仅与s 有关的量,其具体表达式见文献[11]。
把Xt看作发电机的内阻抗,仿照上式可得升压变母线电压的幅值为
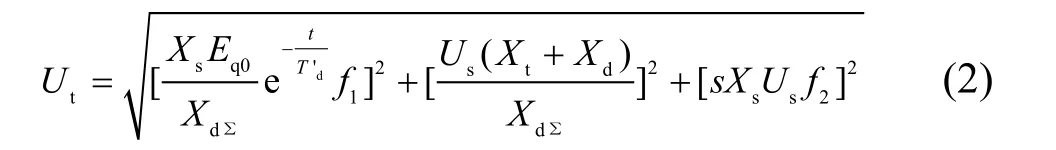
从而可以得到机端电压和升压变母线电压的变化率为

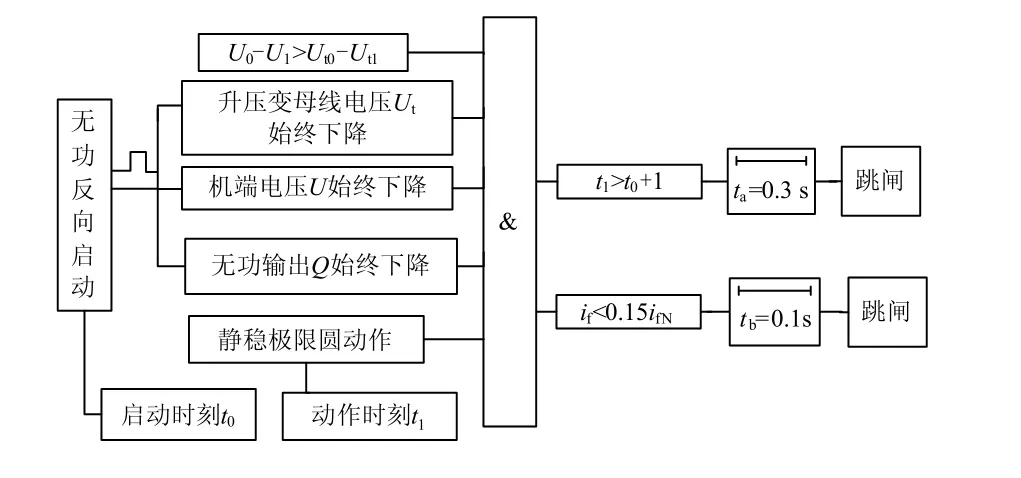
由式(3)知,失磁发电机的无功反向后,有U 当发生部分失磁时,推导方法类似,可得到同样的结论:在失磁发电机无功反向之后、有功开始振荡之前,机端电压和升压变母线电压均始终减小,且机端电压下降速度比升压变母线电压快。 1.1.2 系统振荡时的电压变化规律 振荡分析采用图2的等值两机系统,并假设两等值机电势幅值相等,忽略线路电阻和对地电容。 图2 等值两机系统Fig.2 Equivalent two machine power system 1)系统振荡中心M 落在母线T 外侧时 母线T 内侧点O的电压幅值为[12] 其中:Xeq为两机间的联系电抗;XOM为O点到M间的电抗。可得电压变化率为 2)系统振荡中心M 落在母线O1与T之间时 此时母线O1电压表达式不变。母线T 电压为 式(4)、式(6)的形式是相同的。易知当XO1M>XMT,即振荡中心M 偏向母线T时,同样有 综上可知,当系统振荡中心落在变压器半阻抗以外、且电压下降时,机端电压下降速度比升压变母线电压慢,这与发电机失磁时的电压变化情况相反。需要说明的是,当振荡中心落在变压器半阻抗以内时,这一结论并不成立。 发电机失磁时,发电机无功输出可表示为 系统振荡时,发电机无功输出为 由式(10)、式(11)可知,发电机失磁后、临界失步前,随着功角的增大,无功输出始终下降;系统振荡时,只要δ 在(0,π)内,无功输出随功角的增大始终增加,两者情况相反。 根据式(7),发电机失磁时无功始终下降进而发生无功反向。根据实测数据,无功反向的临界功角δcr多在50º~60º内,小于静稳临界角90°。因此发电机失磁后,无功输出将一直减少至无功反向后,才逐渐失去静稳。通过理论估算及现场实测数据均可发现:除开路失磁外,从发电机无功反向到失去静稳的持续时间至少在1.5 s以上。 根据式(8),发电机功角增加时,只要δ 在(0,π)内,即使越过静稳极限角,发电机无功输出仍一直增加,不会出现无功反向。这与失磁时是相反的。 利用此节得到的特征与振荡中心无关,即使振荡中心落在变压器半阻抗以内,保护也不会误动作。 上节中提到的无功反向到静稳持续时间较长的规律对于开路失磁情况并不满足。失磁类型、失磁程度的多样性,也是造成失磁保护整定困难的原因之一。不同失磁类型的主要特征是转子励磁电流变化的时间常数。经推导可知:短路失磁、部分失磁的时间常数都较大,转子电流衰减较慢;开路失磁的时间常数约等于0,转子电流迅速衰减到零,因此开路失磁时保护拒动率较高[13]。 综合以上的推导可知,发电机失磁(失磁后、失步振荡前)和系统振荡具有以下相异的特征: (1)电压变化特征:失磁时电压始终下降,且机端电压较升压变高压侧母线电压下降速度快;系统振荡时,只要振荡中心落在升压变半阻抗以外,机端电压较升压变母线电压下降速度慢。 (2)无功变化特征:失磁时发电机无功输出始终减小;振荡时发电机从初始状态到静态稳定点,无功输出一直增加。 (3)时间特征:发生短路失磁和部分失磁时,发电机从无功反向到失去静稳时间较长;振荡时从初始状态到失去静稳时间较短。开路失磁时,转子电流迅速减小。 基于上节推导的失磁和振荡场景下电气量变化的不同特征,本文提出电压变化判据、无功变化判据、时间判据检测失磁故障,并考虑到发电机开路失磁时电气量变化快慢与短路失磁、部分失磁时相比差异显著,提出了转子低电流判据作为加速跳闸的辅助判据。新型失磁保护方案原理框图如图3所示。 图3 新型失磁保护原理框图Fig.3 Functional block diagram of new LOF protection 下面具体介绍各个元件的实现和整定原则。 (1)启动元件:保护启动采用“无功反向”元件,并记录启动时刻t0。需要注意的是,若发电机处于进相状态时发生失磁故障,无功功率始终下降,“无功反向”元件不会启动,保护拒动。故在发电机进相运行时可改采用“励磁低电压”元件作为启动元件,按躲开正常进相运行的最低励磁电压整定。启动后应闭锁启动判据,防止故障期间多次启动。 (2)静稳判据:静稳判据由“静稳极限圆动作”元件实现,并记录满足判据的时间t1。静稳判据的主要作用是在检测到失磁特征后启动动作回路,同时也为时间判据和电压判据提供静稳临界时间。 关于静稳极限圆的整定,现有方案一般采用Xsmin整定,这会导致静稳极限圆提前动作;发电机功角较大时也可能误动。在此采用静稳判据的目的是确保保护在发电机失去静稳后才动作;考虑到如今电力系统多运行在大方式下,采用Xsmax可保证动作的可靠性,因而本文采用Xsmax整定静稳极限圆。 (3)电压变化判据:电压变化判据由“机端电压U 始终下降”、“升压变母线电压Ut始终下降”、“U0-U1>Ut0-Ut1”元件实现。其中电压下降幅度的比较采用t0和t1时刻的电压差值,此时电压下降幅度较大,比较精度较高。 (4)无功变化判据:无功变化判据采用“无功输出始终下降”元件,要求在t1-t0时间内,发电机吸收无功且不断增加,与电压变化判据一起保证方案的可靠性。 (5)时间判据:短路失磁、部分失磁时,失磁发电机从无功反向到失去静稳所需时间在1.5 s以上。该判据由时间元件实现。可靠起见,时间比较元件动作值整定为t1>t0+1。 (6)转子低电流判据:发电机开路失磁时,转子电流迅速减小,从无功反向到失去静稳的时间非常短,此时时间判据将失效,故在此引入转子低电流判据。考虑到发电机短路或部分失磁时,时间判据应先于转子低电流判据动作。经估算短路失磁和部分失磁情况下,失去静稳时转子电流一般大于0.151ifN,故整定转子低电流阈值为0.15 ifN。 (7)延迟元件:由于失磁发电机失步后,机端电气量将开始剧烈振荡,本文所提判据将失效。因此,延迟元件的整定除了考虑进一步增强失磁故障判别的准确性外,也应注意发电机从静态失稳到失步的时间。现场失磁故障数据及仿真算例表明,短路失磁、开路失磁情况下,发电机从静态失稳到失步的时间分别至少在1.5 s、0.2 s以上。在保证判据不失效的前提下,为加快保护动作速度,延迟元件分别整定为ta=0.3 s,tb=0.1 s。 为验证本文所提出的新型失磁保护方案的有效性,采用PSASP 仿真软件在测试系统上进行仿真分析,比较现有失磁保护及新型方案的动作情况,以评估新型失磁保护方案的性能。 测试系统采用某省级电网实际系统数据,测试发电机通过单回220kV 线路接入电网。发电机参数如下:SN=100 MWA,Xd=0.520 1,Xq=0.520 1,X′d=0.057 7,Xt=0.042,Xsmax=0.058,Xsmin=0.158,TJ=18.14,T′d0=9.34。 (1)发电机全失磁故障 发电机初始输出运行点为P=3,Q=0.712。在1 s 发生全失磁故障,发电机电气量曲线及阻抗变化轨迹如图4。 图4 发电机全失磁时的电气量及阻抗轨迹曲线Fig.4 Electric quantity curves and apparent impedance path after complete loss-of-excitation 从图中可以看出,无功反向元件1.85 s 动作、静稳极限圆2.96 s 动作,失磁发电机在临界失步前,发电机无功输出迅速下降,机端电压比升压变母线电压下降得更快,新失磁保护方案中的各判据都满足,保护可靠快速动作。 (2)发电机失稳振荡 发电机初始输出运行点为P=3,Q=0.712。升压变出口在1 s 发生三相接地故障,主保护拒动,1.16 s时后备保护切除故障后引发系统失稳振荡。发电机电气量曲线及阻抗变化轨迹如图5。 从图中可以看到,无功反向元件1.7 s 动作,阻抗轨迹1.77 s 进入静稳极限圆,1.97 s 离开,“时间判据”不满足,可保证保护可靠不动作。同时,这段时间内“无功判据”、“电压判据”也都不满足。 图5 失稳振荡时发电机电气量曲线及阻抗轨迹曲线Fig.5 Electric quantity curves and apparent impedance path during unstable swings 对新型失磁保护方案和现有保护方案进行比较分析,以评价保护方案的性能。保护方案设置如下:(1)静稳极限圆+1.5 s 延时跳闸;(2)异步阻抗圆+0.5 s延时跳闸;(3)新型失磁保护方案。 考虑以下两类故障情况:(1)发电机发生失磁故障:包括短路全失磁、部分失磁、开路失磁三种情形;(2)系统发生振荡:包括失稳振荡和稳定振荡。 为测试方案对发电机工况的适应性,选择20种发电机初始运行状态,如图6所示。 图6 发电机初始运行点Fig.6 Initial operation conditions of test unit 分别仿真以上20种工况下发生五种故障时三种失磁方案的动作情况并进行比较,比较结果见表1、表2。 从表1和表2可以看出: 1)动作可靠性。发电机部分失磁时,所有保护方案均正确动作;短路和开路失磁时,现有失磁保护正确动作率较低,新型保护方案均正确动作。另一方面,系统稳定振荡时,三种失磁保护方案均没有误动;系统失稳振荡时,现有失磁保护有误动发生,新型失磁保护可保证正确不动作。 表1 失磁故障下不同方案的正确动作率及动作时间Table1 Correct action rate and average action time of different schemes after loss-of-excitation 表2 振荡故障下不同方案的误动率Table2 Mal-operation rate during swings 2)动作快速性。由于新失磁保护方案采用的判据能可靠区分失磁和振荡,各判据动作后再经较短的延时即快速动作;而现有失磁保护方案中则采用了长延时元件区分失磁和振荡,因此新型保护方案的平均动作时间更短,可显著减小失磁发电机对系统的不良影响。 综上,本文所提出的新型失磁保护方案具有可靠性高、动作速度快的优点,有利于发电机和系统的安全稳定运行。 本文基于机网协调优化涉网保护优化配置的背景,对误动率高且对机组和系统影响较大的失磁保护进行了研究。在发电机失磁和系统振荡过程理论推导的基础上,综合利用发电机失磁过程中电压、无功和功角变化的特征信息,提出了一种新型的失磁保护方案。理论分析和仿真结果表明,新型方案具有可靠性高、动作速度快的优点。 本文对发电机失磁后特征信息进行了深入的挖掘,研究方法为今后失磁保护方案的设计或改进提供了思路。发电机涉网保护的优化,不仅可保障发电机的安全运行,对机网协调发展、防止电网大面积崩溃事故的发生具有重要意义。 [1]王维俭.电气主设备继电保护原理与应用[M].北京:中国电力出版社,1996. WANG Wei-jian.Principle and application of electric power equipment protection[M].Beijing:China Electric Power Press,1996. [2]刘一丹,张小易,崔晓祥.火电厂发电机失磁保护阻抗判据的探讨[J].电力系统保护与控制,2010,38(20):235-237. LIU Yi-dan,ZHANG Xiao-yi,CUI Xiao-xiang.Discussion of thermal power plant generator resistance criterion for loss of excitation protection[J].Power System Protection and Control,2010,38 (20):235-237. [3]殷建刚,彭丰,杨平,等.发电机失磁保护中系统低电压判据的探讨[J].电力自动化设备,2003,23(12):28-31. YIN Jian-gang,PENG Feng,YANG Ping,et al.Discussion on low voltage criterion in field-loss protection[J].Electric Power Automation Equipment,2003,23(12):28-31. [4]刘伟良,陈宏,刘宇,等.由一起发电机失磁事故谈失磁和逆功率保护的设置[J].电力系统保护与控制,2009,37(23):164-166. LIU Wei-liang,CHEN Hong,LIU Yu,et al.Discussion about loss-of-field and reverse-power protection configuration from the generator loss-of-field fault[J].Power System Protection and Control,2009,37(23):164-166. [5]North American Electric Reliability Corporation (NERC).Power plant and transmission system protection coordination[R].NERC,2010. [6]李哲,季学军,王祖光.基于发电机功率变化量的失磁保护辅助加速判据[J].电力系统自动化,2008,32(15):54-56. LI Zhe,JI Xue-jun,WANG Zu-guang.An auxiliary accelerated judgment method for loss of excitation protection based on generator power variation[J].Automation of Electric Power Systems,2008,32(15):54-56. [7]隋佳音,毕天姝,薛安成,等.新型发电机失磁保护加速判据研究[J].电力系统保护与控制,2010,38(20):69-73. SUI Jia-yin,BI Tian-shu,XUE An-cheng,et al.A novel accelerated criterion for loss of field protection[J].Power System Protection and Control,2010,38(20):69-73. [8]de Morais A P,Jr Cardoso G,Mariotto L.An innovative loss-of-excitation protection based on the fuzzy inference mechanism[J].IEEE Trans on Power Delivery,2010,25(4):2197-2204. [9]林莉,牟道槐,孙才新,等.同步发电机失磁保护的改进方案[J].电力系统自动化,2007,31(22):88-93. LIN Li,MOU Dao-huai,SUN Cai-xin,et al.Improvement on loss-of-excitation protection of synchronous generators[J].Automation of Electric Power Systems,2007,31(22):88-93. [10]薛伊琴.发电机失磁保护原理的比较和分析[J].继电器,2005,33(20):33-35. XUE Yi-qin.Comparison and analysis of theory of generator loss of field protections[J].Relay,2005,33(20):33-35. [11]杨嗣彭.同步电机运行方式的分析[M].成都:成都科技大学出版社,1989. YANG Si-peng.Synchronous generator operation analysis[M].Chengdu:Chengdu University of Science and Technology Press,1989. [12]张保会,张毅刚,刘海涛.基于本地量的振荡解列装置原理研究[J].中国电机工程学报,2001,21(12):68-73. ZHANG Bao-hui,ZHANG Yi-gang,LIU Hai-tao.Study on principle of power system separation device based on local electrical parameter[J].Proceedings of the CSEE,2001,21(12):68-73. [13]Glavic M,Van Cutsem T.Detecting with PMUs the onset of voltage instability caused by a large disturbance[C]//IEEE Power and Energy Society General Meeting,Pittsburgh,PA,July,2008:1-8.

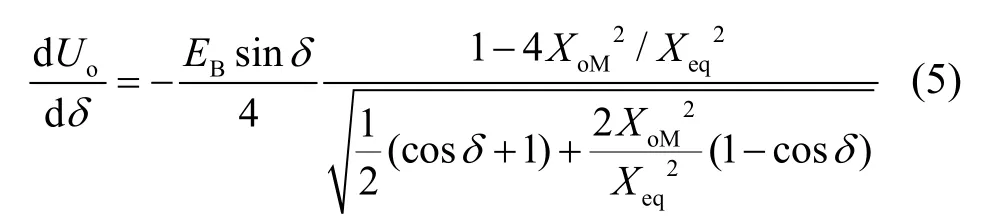

1.2 失磁、振荡时的无功变化规律


1.3 失磁、振荡时的失去静稳规律
1.4 发电机开路失磁特征
1.5 失磁、振荡综合特征
2 新型失磁保护方案
3 仿真验证
3.1 判据有效性验证


3.2 保护方案比较分析



4 结论
