全地面起重机塔臂工况吊重摆振特性研究
2013-05-25高顺德滕儒民田凤帅
高顺德,杨 超,滕儒民,田凤帅,赵 超
(1.大连理工大学 机械工程学院,辽宁 大连 116023;2.大连益利亚工程机械有限公司,辽宁 大连 116023)
全地面起重机具有起重量大、起升高度高、作业半径大以及适应能力强等诸多优点,逐渐成为移动式起重机市场的主力军[1].但较大的起升高度和作业半径会导致起重机在回转过程中吊重的摆振更为明显,从而降低吊装就位精度,同时对起重机臂架系统产生较大的周期性附加动载荷,影响起重机臂架力学性能及整机稳定性.为了提高起重机作业效率和操作安全性,研究回转过程中吊重摆振特性,对于指导全地面起重机的结构设计和控制编程具有重要意义.
目前国内外学者对起重机吊重摆振特性进行了大量的研究,但主要集中在小车-吊重系统.如SINGHOSE W[2]等对龙门式起重机在起升运动时吊重摆动及控制进行了研究.吴晓等[3]根据起重机小车-吊重系统的三维动力学模型建立了吊重摆振的二自由度摆角动力学模型,通过线性简化从模型中找出了影响摆角大小的主要因素.董明晓等[4]基于非惯性参考系中质点相对运动动力学基本方程,建立塔式起重机同时进行变幅、回转、起升运动的情况下载荷摆动动力学方程.王帮峰等[5]采用机器人动力学方法建立吊重摆振的动力学模型并提出了最优调节器理论的控制方案,但所研究起重机模型仅包含主臂.
本文以某1 200t全地面起重机塔臂工况为研究对象,基于机器人动力学理论,将全地面起重机塔臂工况时的结构等效成5个杆件串联的开链机械手形式,建立吊重摆振的动力学方程,对全地面起重机塔臂工况回转过程吊重摆振动态特性进行了研究,分析了影响吊重偏摆角大小的因素.
1 吊重摆振动力学方程
1.1 吊重摆振动力学模型
根据全地面起重机塔臂工况的结构特点(见图1)和机器人相关理论,当只考虑起重机的回转运动,可将全地面起重机等效为具有5个杆件的串联开链机器人系统.如图2所示,全地面起重机塔臂工况的机器人模型,机座0为起重机底盘支撑结构,杆件1为转台,关节变量θ1为转台回转角度,杆件2为主臂,杆件3为塔臂,关节变量θ2,θ3分别为主臂变幅角和塔臂变幅角,杆件5为吊绳和吊重,ri(i=1,2,3,4,5)为各杆件质心到杆件坐标系原点的距离.引入长度和质量均为零的虚拟杆件4,利用与之相关的关节变量θ4,θ5及吊绳的长度来描述吊重相对于吊点的空间摆振位置.在本文研究中,视各杆为刚性,忽略吊绳的质量及吊重尺寸对起重机回转运动的影响,忽略系统阻尼和风载的影响,吊绳的刚度足够大,不考虑其弹性变形.

图1 全地面起重机塔式副臂工况结构图Fig.1 Tower jib operation of all terrain crane
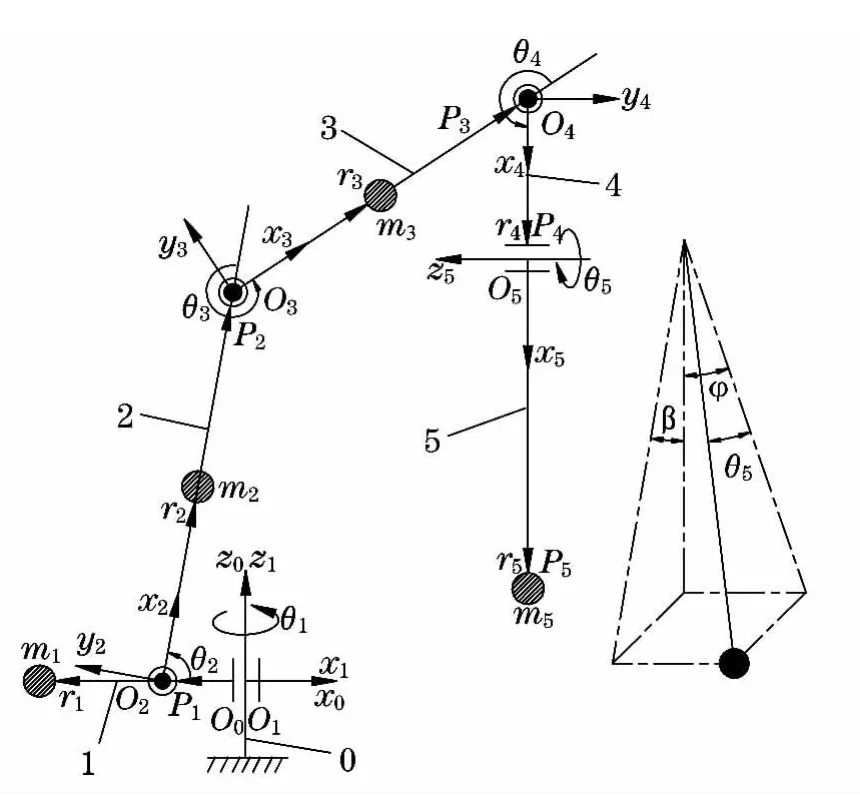
图2 全地面起重机塔臂工况的机器人模型Fig.2 Robotic modeling of all terrain crane with tower jib
采用Denavit-Hartenberg方法确定齐次坐标变换矩阵A,表示相邻两杆件相对位置和方向的关系[6].采用下关节的坐标建立方法建立杆件坐标见图2,则各关节处对应的矩阵为
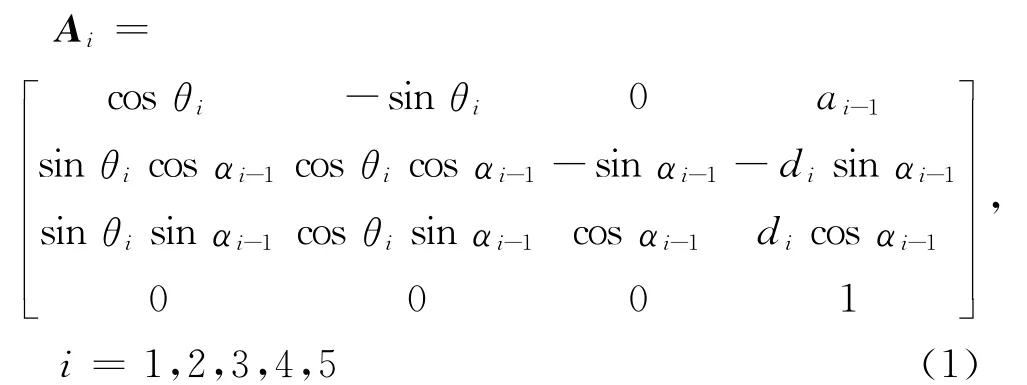
式中:ai-1为杆件的长度,i=1,2,3,4,5;αi-1为杆件的扭角.
由于D-H方法对关节变量的规定,使得用θ4描述吊重在变幅平面内的摆振(径向摆振)并不直观,所以采用图2中径向摆角φ代之,即吊绳在变幅平面上的投影与铅垂线的夹角,由几何关系可得
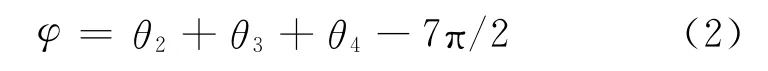
同时,由于在回转过程中径向摆角φ一般较小,可近似地将θ5视为吊重的切向摆角β,即吊绳与变幅平面的夹角.矩阵Ai中参数的取值见表1,其中e为回转轴线到臂架与转台铰点的距离,lzb为主臂长度,ltb为塔臂长度.
1.2 系统动力学方程
利用牛顿-欧拉方法推导系统动力学方程组[6].将转台转速作为系统输入,视为已知.同时由于机座为不动杆件,所以将系统参数

表1 矩阵A参数Tab.1 Parameters of Amatrix
代入牛顿-欧拉正向递交推公式:
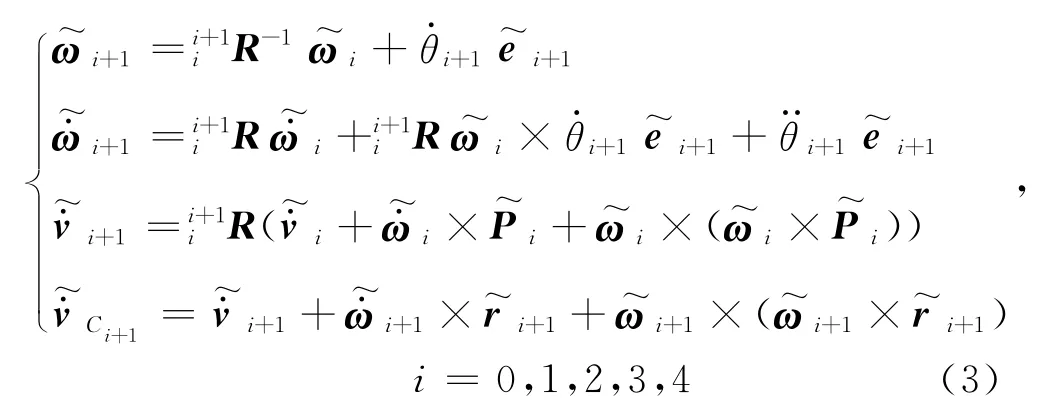
式中:符号上方的波浪线表示该量是在其后下标所表示坐标系中度量的分别为{i}系相对于{i-1}的角速度和角加速度矢量的逆矩阵为{i+1}系向{i}系变换的Ai的旋转子矩阵分别为{i}系原点Oi的线速度和线加速度矢量为第i+1号杆件的执行器在i+1号关节处提供的角速度和角加速度;为指定{i+1}系z轴方向的单位矢量,为在{i}系中描述的{i+1}系原点的位置矢量为杆件i+1在(i+1)系中的线加速度为第i+1号杆件的质心在{i+1}系中的位置矢量.
并因吊重质心处线加速度在杆件5坐标系中的y,z轴分量为零,即则可导出全地面起重臂塔臂工况进行回转运动时的吊重摆振动力学方程组为
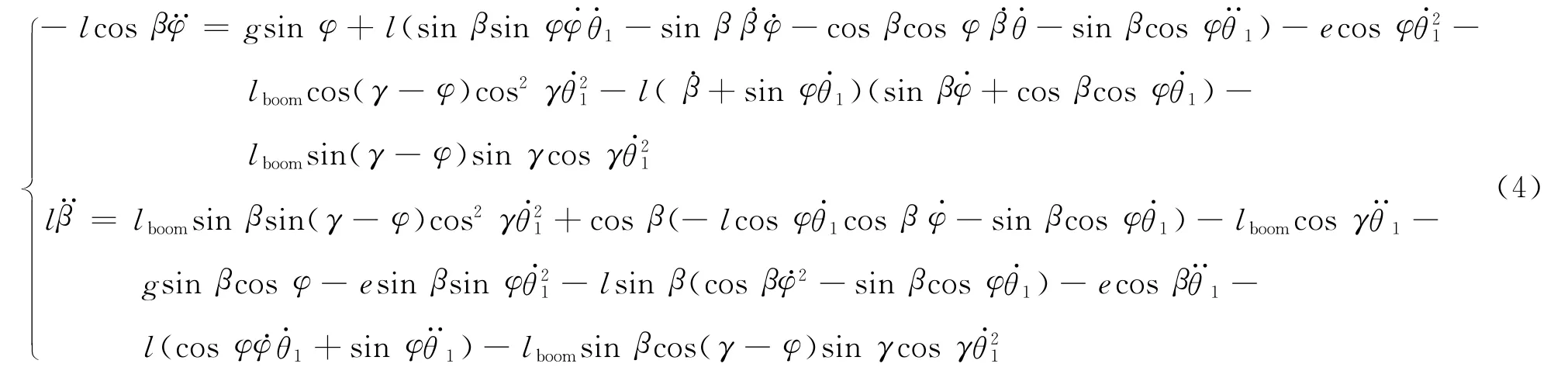
式中:l为吊重质心到塔臂悬吊点的距离(吊绳长度);为主臂长度,ltb为塔臂长度;γ=θ2-asin(ltbsin(θ3-π)/lboom).
2 吊重摆振特性研究
回转过程中产生的切向惯性力和径向离心力会引起吊重在径向和切向的摆振,但二者的摆振并非独立进行,而是相互影响共同作用使吊重在空间产生一个复杂的振动.这一吊重摆振动态特性可以结合回转运动的特点,利用动力学方程(4)进行研究.
2.1 径向和切向摆振研究
选取分析工况参数为:主臂长度为lzb=17.2m,塔臂长度为ltb=36m,吊绳长度为l=5m,主臂仰角为θ2=76°,工作幅度为lfd=36m,额定起重量为65t,最大回转角速度为n=1.0r·min-1.
如图3所示,表示在100s回转过程中吊重在两个方向上的摆振情况,0~10s为匀加速启动阶段,10s之后为匀速回转阶段.从图中可得:对于切向摆振,在加速阶段,吊重在惯性冲击载荷的作用下以图中所示基线为对称轴摆振,基线所在位置的摆角为2.20°,与回转惯性力作用下吊重受力平衡时的切向摆角相等;在匀速回转阶段,由于惯性力消失及不考虑系统阻尼,吊重在初始激励的作用下以铅垂线为对称轴摆振.对于径向摆振,在加速阶段,吊重的摆角逐渐增大,并发生轻微的振动;在匀速回转阶段,吊重以图中所示基线为对称轴摆振,基线所在位置的摆角为2.31°,与回转离心力作用下吊重受力平衡时的径向摆角相等.另外由图3可得:切向和径向的摆振均以一定的周期循环,采用傅立叶变换(FFT)分析得到吊重在两个方向上摆振的频谱图(见图4),由图4可得两个方向上的摆振频率均为0.23Hz,吊绳长度为5m的简单钟摆其摆振频率为0.22Hz,二者近似相等.
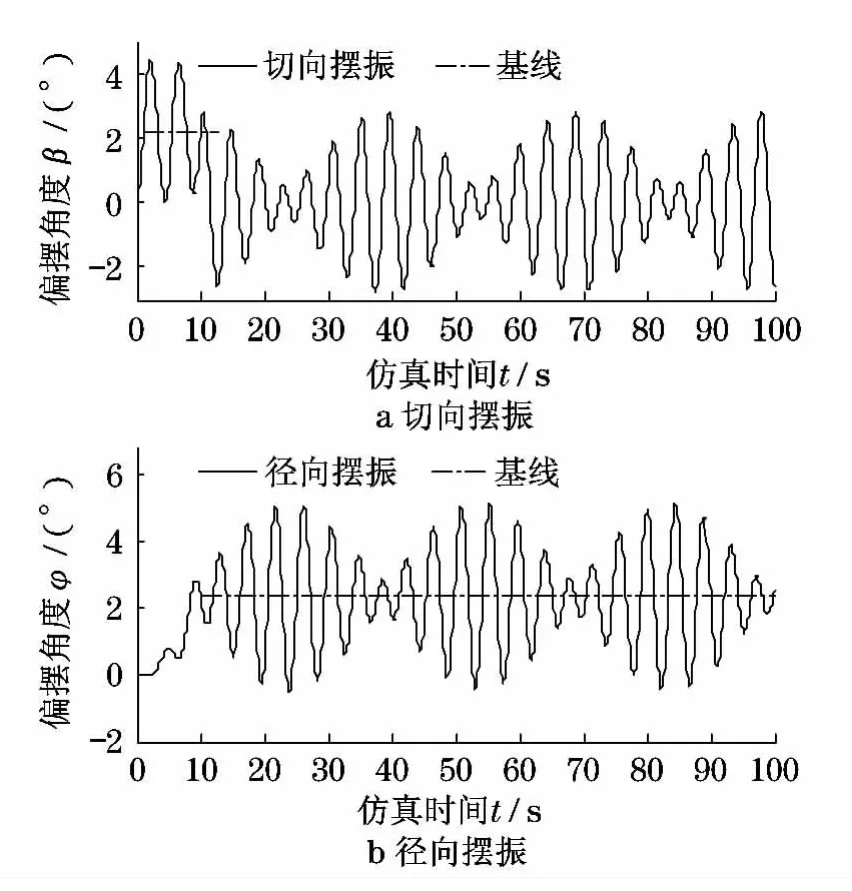
图3 100s回转过程中吊重的摆振Fig.3 Load vibration during 100sof the slewing motion
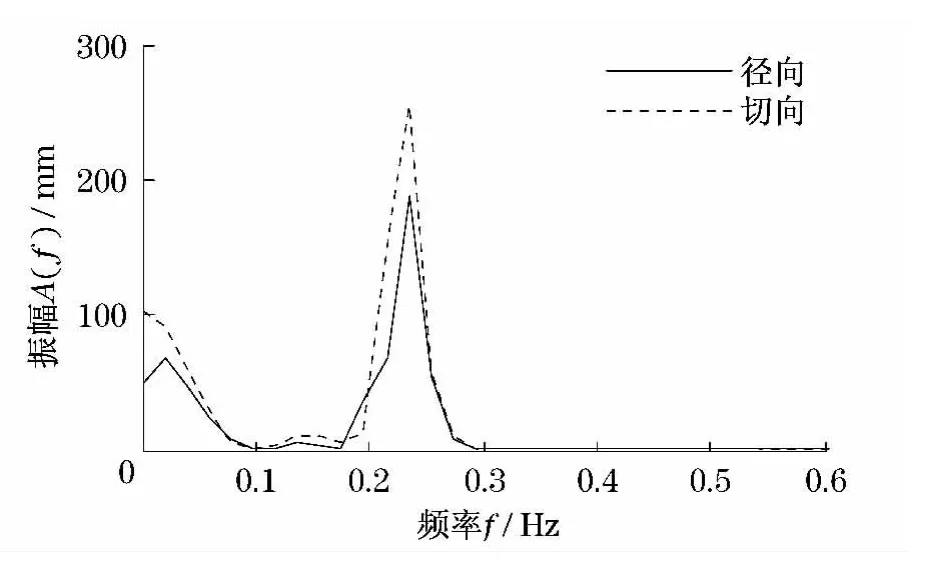
图4 吊重摆振频谱图Fig.4 Spectrum diagram of theload vibration
如图5所示,表示在360°回转过程中吊重在两个方向上的摆振情况.从图5中可得:最大稳态径向摆振幅度(注:启动或制动时的摆振称瞬态摆振,匀速回转或静止时的摆振称稳态摆振)发生在稳态切向摆振幅度接近最小值时,同样反之亦然.同时每回转90°以后,径向和切向的稳态摆振均发生较明显的转换,两个方向上的稳态摆振幅度关于90°的回转距离几乎是对称的.在回转90°后,初始位置时的径向变成切向,而初始位置时的切向变成径向,这一空间位置及方向的变化和特点,导致了吊重在回转时表现出如图5所示的摆振动态特性,而且系统摆振的最原始激励主要来源于回转加速启动时切向的惯性冲击载荷,径向摆振是随着回转距离的变化由切向摆振传递而来.
如图6所示,表示在不同加速斜坡信号时吊重在两个方向上的摆振情况.从图6中可得:对于切向摆振,在斜坡信号时间为11s时,信号结束时刻吊重所在空间位置的幅度较大,导致稳态切向摆振幅度较大.在斜坡信号时间为9s时,信号结束时刻吊重所在空间位置的幅度较小,导致稳态切向摆振幅度较小.对于径向摆振,其稳态摆振幅度主要受切向摆振幅度的影响,所以如图6所示,吊重径向摆振与切向摆振有着相同的规律.
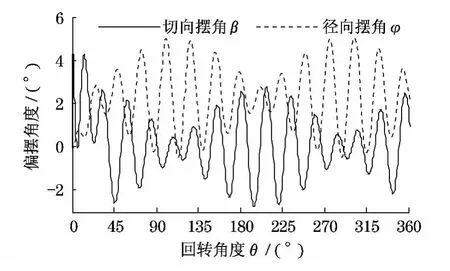
图5 360°回转过程中吊重的摆振Fig.5 Load vibration during 360°of the slewing motion
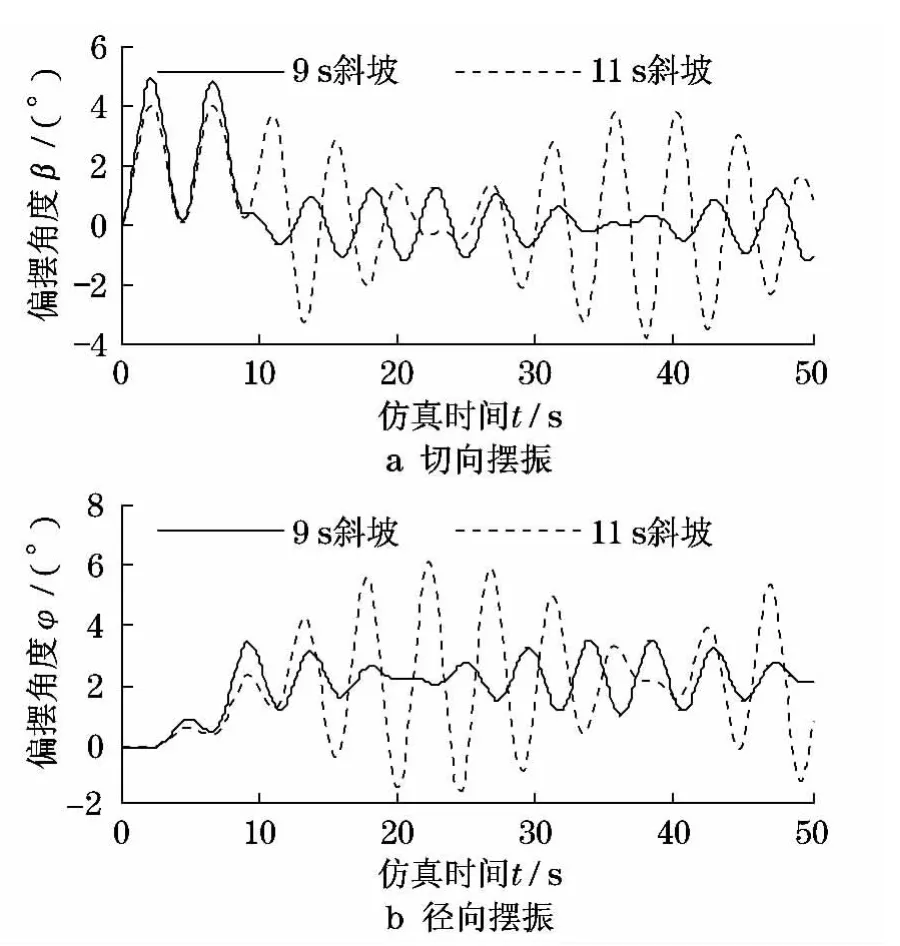
图6 不同加速斜坡信号时吊重摆振Fig.6 Load vibration in different speed ramp signals
如图7所示,表示在不同时刻制动时吊重在两个方向上的摆振情况.从图7中可得:对于切向摆振,在12s开始制动时,制动引起的摆振与启动引起的摆振协调一致,增强了由启动引起的切向摆振,导致稳态切向摆振幅度要比瞬态时的大.在13s开始制动时,制动引起的摆振与启动引起的摆振不一致,削弱了部分由启动引起的切向摆振,导致稳态切向摆振幅度要比瞬态时的小.同样如图7所示,吊重径向摆振与切向摆振有着相同的规律.
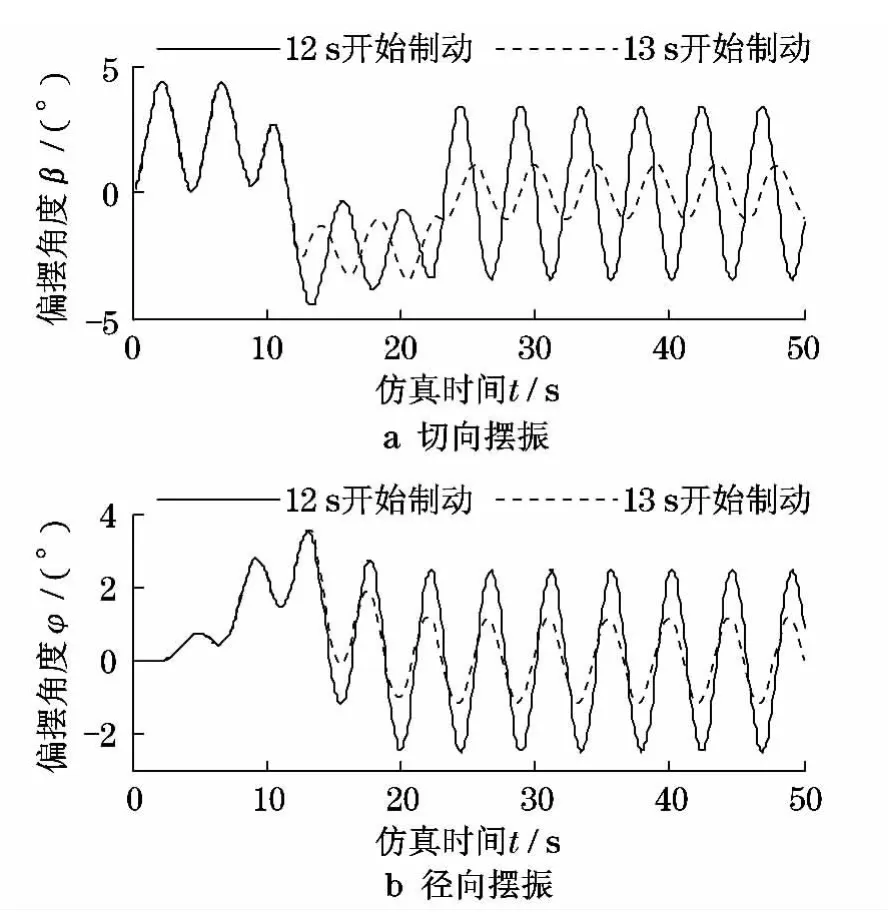
图7 不同时刻制动时吊重摆振Fig.7 Load vibration in different times for braking
2.2 影响偏摆角大小因素研究
影响起重机回转偏摆角大小的因素很多,主要有:吊绳长度l、工作幅度lfd、加速斜坡时间t等,这些因素综合影响了起重机的工作效率和安全.本部分将研究这些因素与偏摆角的关系及其对偏摆角大小的影响.选取的工况为:主臂长度为lzb=17.2m,塔臂长度为ltb=36m,主臂仰角为θ2=76°,最大回转角速度为n=1.0r·min-1.
如图8所示,表示在特定的绳长(l=10m)和加速斜坡信号(t=5s)下,切向最大偏摆角β和径向最大偏摆角φ随工作幅度变化曲线.从图中可得:两个方向的偏摆角均随工作幅度的增加而变大且二者成线性关系.

图8 偏摆角随工作幅度变化规律Fig.8 Regularity for partial vibration angle with working range changing
如图9所示,表示在任意一幅度(在此取lfd=36m)下,分别在l=6~21m绳长时,切向最大偏摆角β随斜坡时间变化曲线.从图可得:随斜坡时间增加,切向偏摆角减小且趋于稳定.同时当斜坡时间较短时,绳长越短,切向偏摆角越大,当斜坡时间大于一定值时,绳长越长,切向偏摆角越大.如图10所示,表示在任意一幅度(在此取lfd=36m)下,分别在t=1~8s斜坡时,切向最大偏摆角β随吊绳长度变化曲线.从图可得:当斜坡时间较短时,绳长越短,切向偏摆角越大,当斜坡时间大于一定值时,绳长越长,切向偏摆角越大.同时当绳长超过一定值后切向偏摆角趋于稳定.径向最大偏摆角φ与切向最大偏摆角β有着相同的变化规律,在此不再赘述.
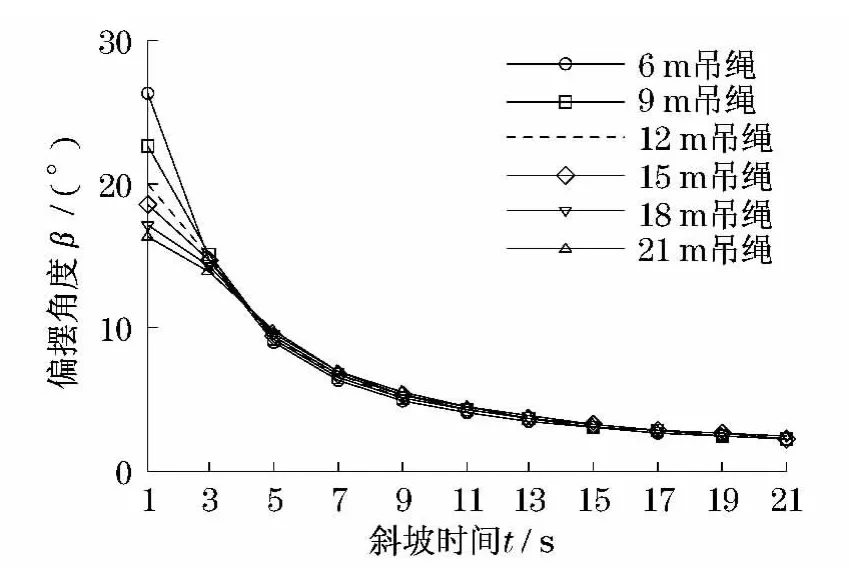
图9 切向偏摆角随斜坡时间变化规律Fig.9 Regularity for partial vibration angle with ramp time changing
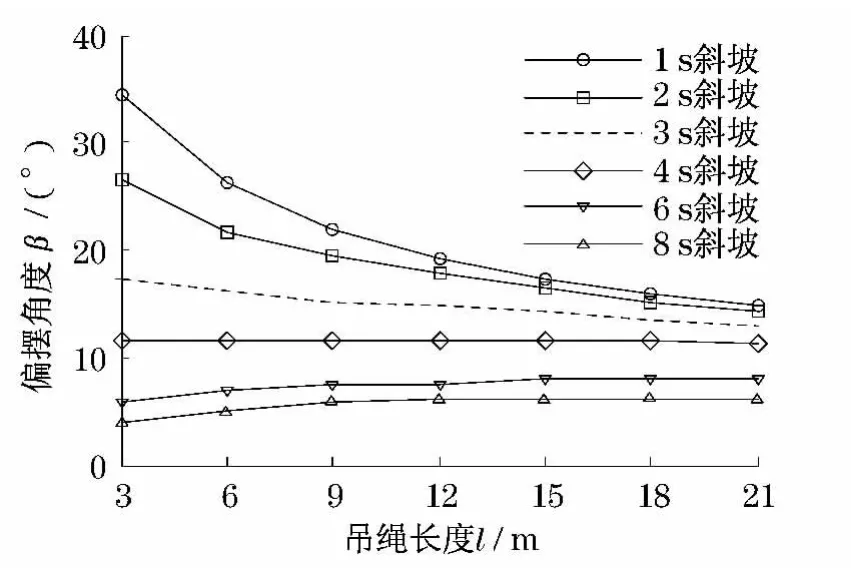
图10 切向偏摆角随吊绳长度变化规律Fig.10 Regularity for partial vibration angle with cable length changing
3 结论
本文利用机器人动力学理论建立吊重摆振的动力学方程,对全地面起重机塔臂工况回转吊重摆振动态特性进行分析研究.通过研究可知:
(1)吊重在切向和径向两个方向上的稳态摆振随着回转时间均以一定的周期循环,二者摆振频率相等且与等绳长简单钟摆的摆振频率近似相等.同时,最大稳态径向摆振幅度发生在稳态切向摆振幅度接近最小值时,反之亦然,而且两个方向上的摆振关于90°的回转距离是对称的.
(2)系统摆振最原始激励主要来源于回转加速启动时切向惯性冲击载荷,径向摆振是随着回转距离的变化由切向摆振传递而来.启动加速停止时刻和制动开始时刻对吊重在切向和径向两个方向上的稳态摆振幅度均有较大影响.
(3)吊重切向最大偏摆角和径向最大偏摆角会随着工作幅度的增加而变大,随启动加速时间的增加而变小,吊绳长度对偏摆角的影响因斜坡时间的不同而不同.
[1]贾体锋,张艳侠.全地面起重机关键技术发展探析[J].建筑机械,2011(1-2):55-61.JIA Tifeng,ZHANG Yanxia.Discuss and analyze the key technique of all-terrain crane[J].Construction Machinery,2011(1-2):55-61.
[2]SINGHOSE W,PORTER L,KENINSON M.Effects of hoisting on the input shaping control of gantry crane[J].Control Engineering Practice,2000,8(10):1159-1165.
[3]吴晓,钟斌,张则强.小车吊重系统摆振动力学模型及仿真[J].计算机仿真,2007,24(11):316-319.WU Xiao,ZHONG Bin,ZHANG Zeqiang.A dynamic model of load sway for trolley load system and its simulation[J].Computer Simulation,2007,24(11):316-319.
[4]董明晓,郑康平,姜红,等.塔式起重机载荷摆动特性研究[J].机械科学与技术,2004,23(8):976-978.DONG Mingxiao,ZHENG Kangping,JIANG Hong,et al.Research on payload oscillation behavior of a tower crane[J].Mechanical Science and Technology,2004,23(8):976-978.
[5]王帮峰,张瑞芳,张国忠.回转起重机吊重摆振的动力学模型与控制[J].中国机械工程,2001,12(11):1214-1217.WANG Bangfeng,ZHANG Ruifang,ZHANG Guozhong.Dynamic model and control of slewing crane load sway[J].China Mechanical Engineering,2001,12(11):1214-1217.
[6]王庭树.机器人运动学及动力学[M].西安:西安电子科技大学出版社,1990.WANG Tingshu.Robot kinematics and dynamics[M].Xi’an:Xidian University Press,1990.
