基于时域多普勒校正和EEMD的列车轴承道旁声音监测故障诊断方法研究

刘 方，沈长青，何清波，胡 飞，张 翱，孔凡让

列车轴承故障是列车故障的主要类型［1］。美国的一项统计表明，每年大约有50起跟轴承相关的列车出轨事故发生［2］。轴承故障会影响列车行驶安全，严重的会导致轴承的车轴、轴套或车轮轮箍踏面断裂或破碎，最终导致列车出轨。对列车轴承的故障诊断重点在于在线发现其早期故障并及时预警，避免故障严重时造成的重大损失。

列车轴承道旁声音监测故障诊断系统形成于20世纪80年代［1］，采用轨边监测麦克风来获取轴承运行时发出的声音，可以发现轴承早期故障，但也因为技术难点存在有些故障不能检测以及故障定位难的缺点［3］而酿成灾难性后果［4］。所以，对于该系统来说，提高故障诊断的准确度和可靠度是研究的重点和难点。

在列车轴承道旁声音监测故障诊断系统中，由于麦克风放置位置与铁轨之间不可忽略的距离以及在列车高速行驶时轴承声源移动相对麦克风存在横向速度，因此造成测量信号的多普勒畸变，这种多普勒畸变会带来测量信号的频移、频带扩展和幅值调制等问题［5］，给基于频率分析的信号处理技术带来了困难，降低了故障诊断的准确度。

在其他一些涉及运动声源声信号处理的领域也存在多普勒效应的干扰，国内外学者提出了相应的解决办法。例如在水下通信领域，Stojanovic等［6］提出了用锁相环技术(PLL)进行多普勒声音信号校正。在车辆噪声定位与测量领域，杨殿阁等［7］提出非线性时间映射法，基于运动声源的声源特征函数，在时域消除多普勒效应，取得了较好的结果。然而以上方法具有一定的领域局限性，并不完全适用于列车轴承道旁声音监测故障诊断系统，目前国内关于列车轴承道旁监测声音信号的多普勒校正方面的文章鲜有发表。

EEMD，即整体平均经验模态分解，是由 Huang等［8］提出的一种有效的非平稳信号分析方法，其本质是将信号从高频至低频分解至有限个反映不同振动模态的本征模态函数(IMF)。同时，EEMD方法利用高斯白噪声具有频率均匀分布的特性，使混入白噪声的信号在不同尺度上具有连续性，可以有效解决经验模态分解的模态混叠问题［9］。陈略等［10］将 EEMD 方法与1.5维谱方法相结合，对机车走行部齿轮箱齿轮裂纹故障微弱特征的提取;郑旭等［11］应用改进的EEMD方法分离柴油机活塞敲击引起的机械激励成分与燃烧爆发激励成分，诊断主要振动源;曹冲锋等［12］利用 EEMD方法对大型旋转机械非平稳信号进行去噪;Lei等［13］利用EEMD方法对转子信号进行分析，都取得较为理想的效果。

本文提出了一种结合时域多普勒校正和EEMD的列车轴承道旁声音监测故障诊断方法，首先对列车轴承故障声音信号在时域内进行多普勒校正，然后利用EEMD方法提取蕴含故障信息的本征模态信号并计算其包络谱来判断轴承是否存在故障。将该方法用于列车轴承故障声音信号的分析，分析结果表明该方法能有效去除多普勒效应并能够有效提取列车轴承故障特征。

1 时域多普勒校正方法

如图1所示，被测列车轴承声源从t=0时刻开始从A点出发，相对于空气介质以速度V沿图中所示方向运动，在运动过程中其辐射出的声音信号经过一段传播距离后到达麦克风处。设在从A点到B点的这段距离内麦克风所采集到的声音为该轴承的有效信号。

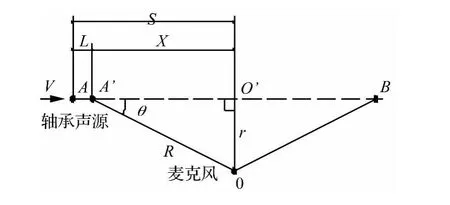
图1 运动模型示意图Fig.1 Kinematic model

由于火车车速较高，麦克风采集有效信号时间较短，因此在从A点到B点的这段距离内轴承声源的速度V可以近似看做是恒定的。

假设声源在tr时刻到达A'点，此时声源振幅为P，声源距离麦克风距离为R，则该振幅需经过dt=R/c(c为声音在空气中的传播速度)时间到达麦克风位置O点，到达时刻为:

其中R可由几何关系计算:

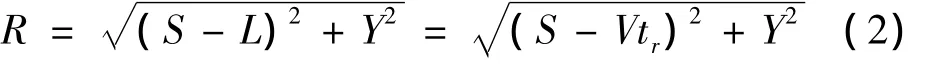
将式(2)代入式(1)得:

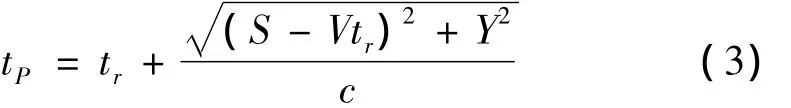
利用上式即可计算到达时刻序列并作为插值拟合时间序列来对采集到的多普勒畸变信号进行插值重采样。

由于声源与麦克风之间的距离随时间不断变化，麦克风采集到的信号幅值受到调制，在重采样过程中须对此信号进行幅值解调还原。

在列车速度为亚声速的情况下，考虑列车轴承声源为单极子点声源，并且传播介质为理想流体，即不存在粘滞性，没有能量损耗。根据莫尔斯声学理论，从波动方程和运动关系出发推导可得［14］:

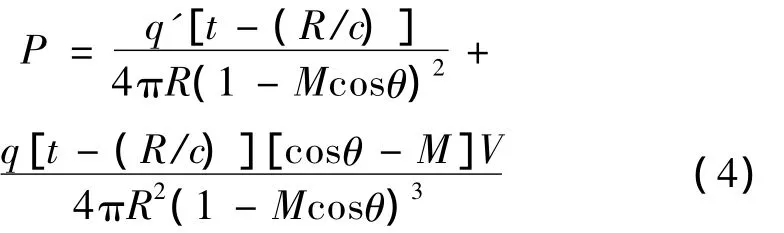
其中:P为麦克风处采集到的声压，q为单极子点声源质量总流率，q'=∂q/∂t，t为运行时刻，R 为发声时刻声源与麦克风之间的距离，c为声音在空气中的传播速度，θ为发声时刻声源和麦克风连线与声源运动方向之间的夹角，V为声源的移动速度，M=V/c为马赫数。式(4)两项中的第一项表示按传播距离衰减的声场辐射项，第二项为近场效应。当声源移动马赫数低于0.2的时候，与第一项相比，第二项为小量［15］，可以忽略不计。因此收到的声压为:

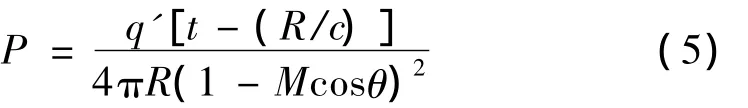
上式可写为:

其中:

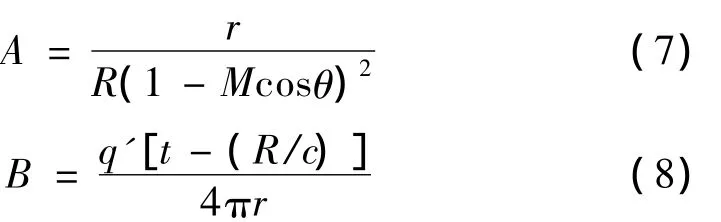
上式中r为麦克风与声源运动直线之间的垂直距离。从表达式上可以看出B为当声源静止时距离声源为r处的声压函数，可以看作需要恢复出的声源信号，R/c为声波从声源传到麦克风所需的时间。因此，A即为由于相对运动而产生的声压幅值调制函数，其逆函数A-1可作为幅值解调函数。若设采集到的多普勒畸变信号为x，则幅值解调后的信号为:

经过幅值解调和插值重采样即可去除多普勒效应，该校正方法的步骤总结如下:

(1)确定重采样频率f后产生重采样时间序列{tr}={0，1/f，2/f，…(N-1)/f};

(2)根据公式(3)和步骤(1)中产生的重采样时间序列计算插值拟合时间序列{tP(i)}，i=1，2…N;

(3)用公式(7)和(9)对畸变信号{x(i)}进行幅值还原处理得到{xP(i)}，i=1，2…N;

(4)用步骤(2)中得到的{tP(i)}对步骤(3)中得到的{xP(i)}进行插值拟合重采样处理，得到幅值序列{xr(i)}，i=1，2…N;

(5)得到校正信号xr(tr)。

2 EEMD基本原理与方法

EEMD是由Huang等提出的一种有效的非平稳信号分析方法，可以将任意非线性、非平稳信号分解为若干具有不同振动模态的本征模态函数(IMF)和余项。传统的经验模态分解方法，由于异常事件(如脉冲干扰等)的存在，导致物理过程的重叠，即产生本征模态函数的模态混叠问题。在经验模态分解方法基础上，EEMD，即整体平均经验模态分解方法引入白噪声进行多次分解求平均，通过白噪声缓和异常事件的局部干扰，从而有效解决模态混叠问题。

本征模态函数需要满足如下条件［10］:

(1)极值点数与过0点数必须相等或者最多相差一个;

(2)在任意时间点上，由信号局部极大值确定的上包络线和由局部极小值确定的下包络线的均值为0。

对于给定的信号x(n)，运用EEMD进行处理的步骤如下:

(1)在原始信号中多次加入高斯白噪声序列，形成混入噪声信号集合:

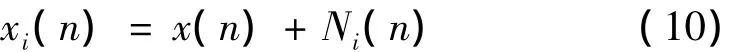
(2)寻找xi(n)极大值和极小值点，通过三次样条曲线拟合出信号的上包络和下包络并对包络求平均，得到均值序列m(n);

(3)从xi(n)中去除均值序列m(n)得到待检测信号，根据本征模态函数条件判断待检测信号是否为本征模态函数，若不满足，重复步骤(2)处理待检测信号，直至满足本征模态函数条件;

(4)计算剩余信号:

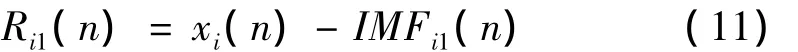
其中:Ri1(n)为剩余信号，IMFi1(n)为本征模态函数;

(5)将剩余信号作为待处理信号，重复(2)、(3)，依次获得 IMFi1(n)、IMFi2(n)，…，IMFik(n);

(6)对步骤(1)中获得的下一个混入噪声信号同样经过步骤(2)至步骤(5)，获得各自的本征模态函数;

(7)将上述对应的IMF进行整体平均，消除多次混入的白噪声对真实本征模态函数的影响:

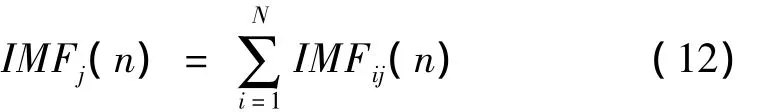
式中:N为本征模态函数数量，IMFij(n)第i个混入噪声信号的第j个本征模态函数。

3 基于时域多普勒校正和EEMD的列车轴承道旁声音监测故障诊断方法

该方法的算法流程如图2所示，首先利用本文提出的时域多普勒校正方法对道旁监测麦克风采集到的声音信号进行校正，然后对校正信号进行EEMD分解获得本征模态信号并利用峭度值选择蕴含故障信息的IMF分量，最后计算选取的IMF分量的包络谱进行诊断。

4 列车滚动轴承道旁声音监测故障诊断应用

为验证该方法的有效性，本文对某型号列车滚动轴承的多普勒试验信号进行处理。试验中所采用的轴承型号为NJ(P)3226XI，该型号为我国列车使用的单列向心短圆柱滚子轴承主要型号，其详细参数如表1所示。

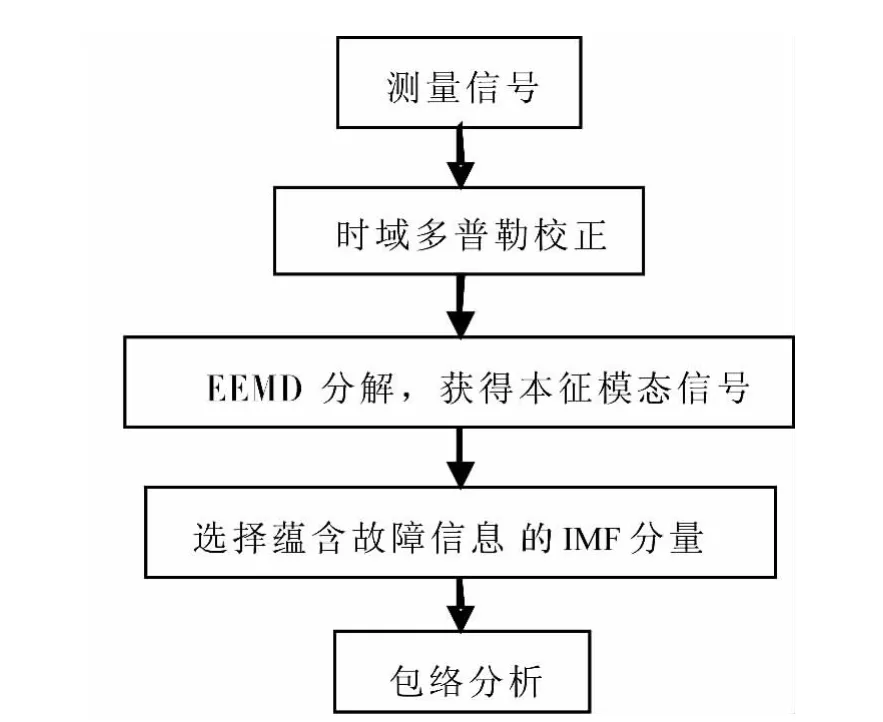
图2 基于时域多普勒校正和EEMD的列车轴承道旁声音监测故障诊断方法流程图Fig.2 The flow chart of the proposedwayside acoustic fault diagnosis method for locomotive bearings combining time-domain Doppler effect correction and EEMD

表1 NJ(P)3226XI轴承参数Tab.1 The specification of the tested bearing NJ(P)3226XI

试验分为两个步骤:第一步，利用图3所示装置获得故障轴承在负载状态运转时发出的声音信号;第二步，将第一步获得的轴承信号保存为wav格式文件，并利用全频音箱播放作为列车轴承声源，将此声源放置在匀速直线运动的汽车上，在声源高速匀速直线运动的同时利用麦克风采集声音信号。

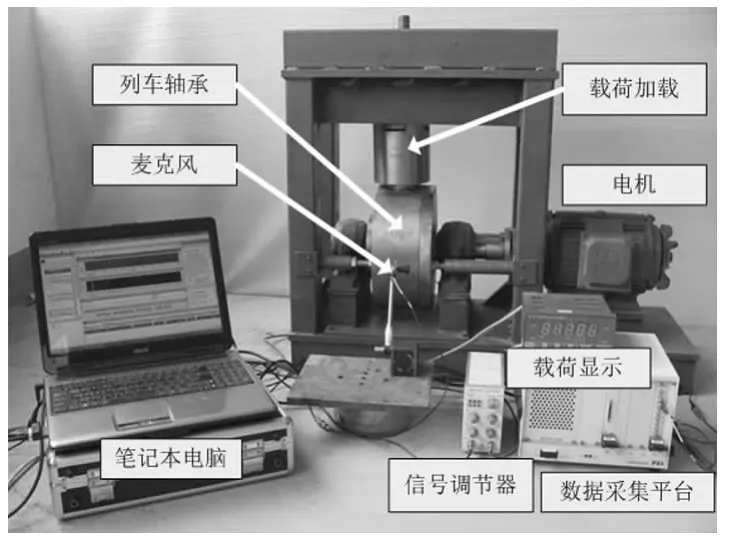
图3 列车轴承实验平台Fig.3 Test bench of the locomotive bearing

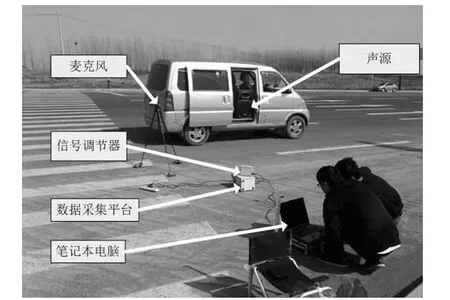
图4 多普勒实验现场Fig.4 Scene of the Doppler experiment

如图5所示，轴承故障采用线切割方式人为加工而成，轴承内外圈的切缝均为0.18 mm。实验中轴承负载为3 t，转速为1 430 r/min，采样频率为50 kHz，车速为108 km/h，测量时麦克风距离轴承声源运动直线距离为2 m。

实验中麦克风选用丹麦B＆K公司的声压场麦克风4944-A，采集卡选用美国NI公司的PXI-4472动态信号采集模块，采集箱选用美国NI公司PXI-1033机箱。

图5 列车轴承故障Fig.5 The locomotive bearing fault

轴承外圈故障特征频率表达式为:

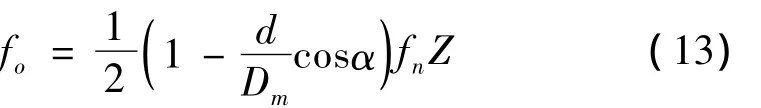
内圈故障特征频率表达式为:

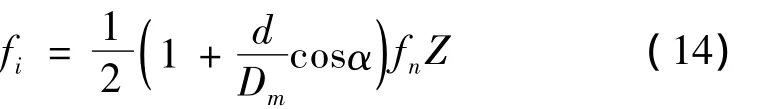
其中:Z表示滚子数目，d表示滚动体直径，α为轴承压力角，Dm为轴承滚道节圆直径，fn为旋转频率。当外圈产生缺陷时，Z个滚珠滚过外圈上该缺陷的频率即为式(13)对应频率，同理，当内圈产生缺陷时，Z个滚珠滚过内圈上该缺陷的频率即为式(14)对应频率，结合表1中相关参数，计算得出实验时外圈和内圈故障特征频率分别为 1 38.6 Hz和 1 94.9 Hz。

图6为轴承外圈存在局部故障时麦克风采集到的道旁声音信号及其包络谱，从其包络谱可以看出由于多普勒效应的干扰，在故障频率处产生了15 Hz的频带扩展，利用本文提出的诊断方法首先对其进行时域多普勒校正，图7为校正步骤中需要的插值拟合时间序列和幅值解调函数，首先利用幅值解调函数进行幅值解调，然后进行插值拟合重采样，得到校正信号如图8(a)所示，从波形上可以看出信号幅值得到了解调恢复。从图8(b)可以看出故障频率较为尖锐和准确，但由于噪声成分较大，故障频率成分难以分辨，利用EEMD方法对校正信号进行分解，图9为校正信号经过EEMD分解后前三阶本征模态信号，按照EEMD分解后本征模态信号按照由高频到低频的排列准则，通过计算，第二阶本征模态信号峭度值为14.201，高于其他任何本征模态信号，故采用第二阶本征模态信号进行包络分析，分析结果如图10所示，从图中可以清晰看出故障频率成分及其二倍频成分，表明包含故障成分信息的成分被成功提取，说明了该方法的有效性。

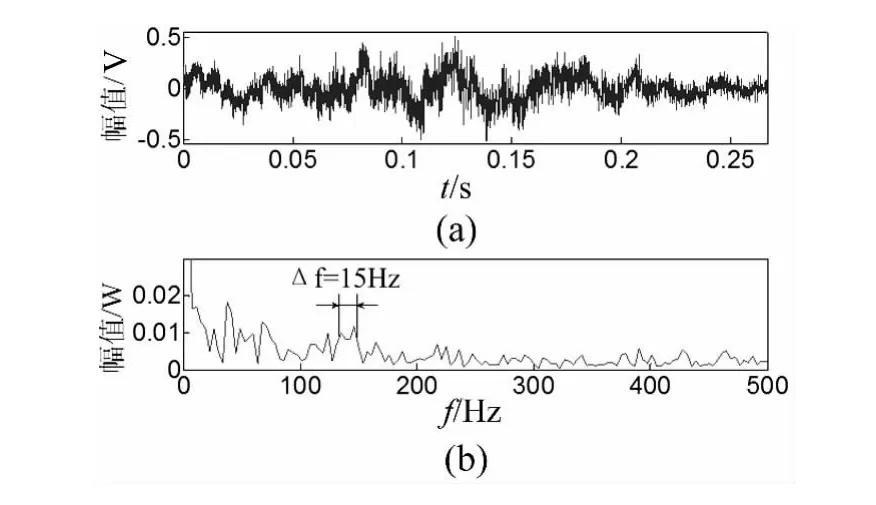
图6 (a)外圈故障轴承声音信号;(b)外圈故障轴承声音信号包络谱Fig.6(a)The raw outer race fault acoustic signal and(b)its envelope spectrum

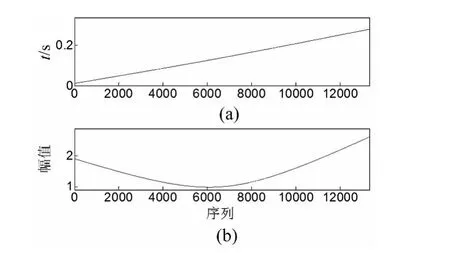
图7 (a)插值拟合时间序列;(b)幅值解调函数Fig.7(a)Time-vector for interpolation and(b)Amplitude demodulation function

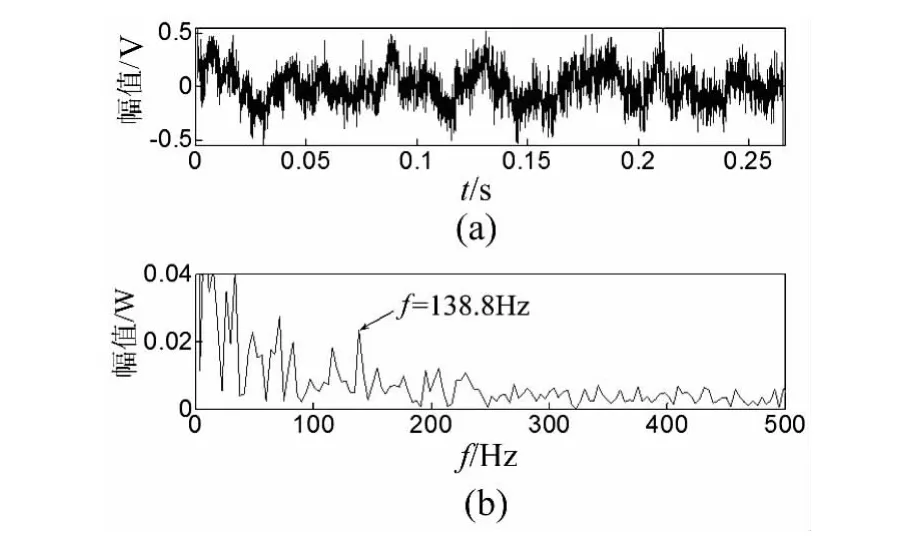
图8 (a)多普勒校正信号;(b)多普勒校正信号包络谱Fig.8(a)Doppler effect corrected signal and(b)its envelope spectrum

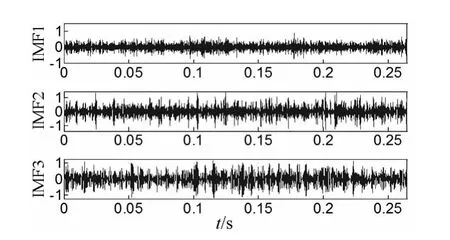
图9 多普勒校正信号经EEMD分解前三阶本征模态信号Fig.9 The first 3 IMFs of the Doppler effect corrected signal decomposed by EEMD method

图11 为轴承内圈存在局部故障时麦克风采集到的道旁声音信号及其包络谱，从其包络谱可以看出由于多普勒效应的干扰，在故障频率处产生了较大的频移现象。

利用本文提出的诊断方法首先对其进行时域多普勒校正，图12为校正步骤中需要的插值拟合时间序列和幅值解调函数，首先利用幅值解调函数进行幅值解调，然后进行插值拟合重采样，得到校正信号如图13(a)所示，从图13(b)可以看出故障频率较为尖锐和准确，但由于噪声成分较大，故障频率成分难以清晰分辨，利用EEMD方法对校正信号进行分解，图14为校正信号经过EEMD分解后前三阶本征模态信号，按照EEMD分解后本征模态信号按照由高频到低频的排列准则，通过计算，第三阶本征模态信号峭度值为13.8，高于其他任何本征模态信号，故采用第三阶本征模态信号进行包络分析，分析结果如图15所示，从图中可以清晰看出故障频率成分及其二倍频成分。以上处理结果表明包含故障成分信息的成分被成功提取，说明了该方法的有效性。

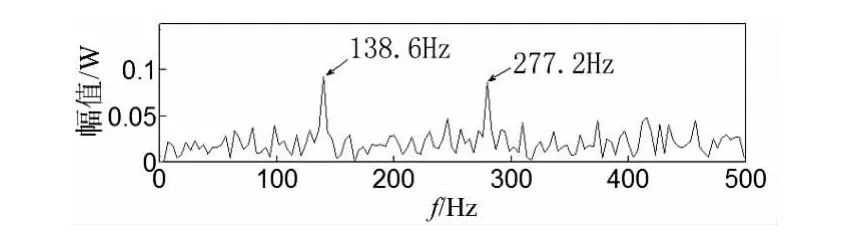
图10 第二阶本征模态信号包络谱Fig.10 Envelope spectrum of the IMF2

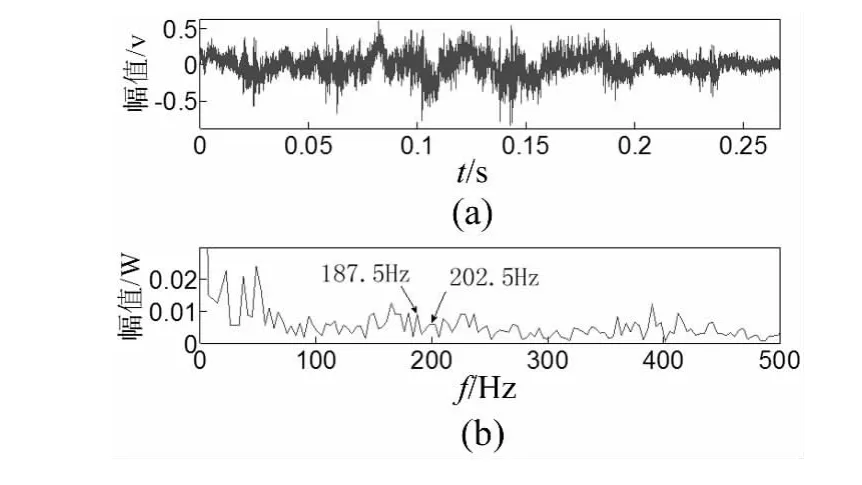
图11 (a)内圈故障轴承声音信号;(b)内圈故障轴承声音信号包络谱Fig.11(a)The raw inner race fault acoustic signal and(b)its envelope spectrum

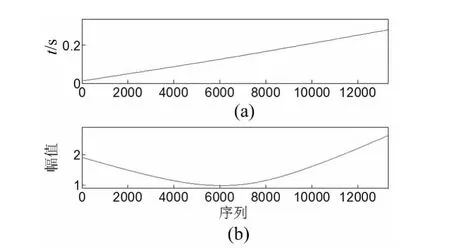
图12 (a)插值拟合时间序列;(b)幅值解调函数Fig.12(a)Time-vector for interpolation and(b)amplitude demodulation function

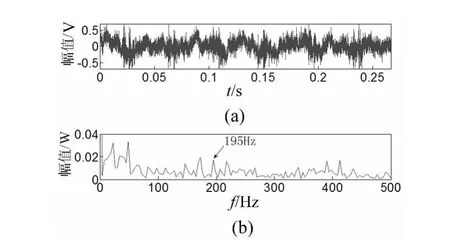
图13 (a)多普勒校正信号;(b)多普勒校正信号包络谱Fig.13(a)Doppler effect corrected signal and(b)its envelope spectrum

同时在故障频率195Hz附近产生了等间距分布的其他频率成分，笔者分析产生这种现象的原因是轴承在重载(3 t)工况下内圈故障点与滚子之间的接触力大小呈现周期性(周期=旋转周期)变化，因此故障频率会受到旋转频率(24.4 Hz)的调制。

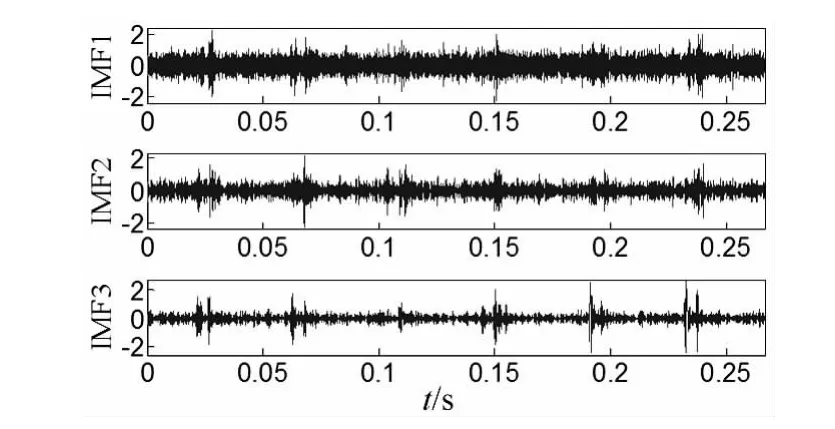
图14 多普勒校正信号经EEMD分解前三阶本征模态信号Fig.14 The first 3 IMFs of the Doppler effect corrected signal decomposed by EEMD method

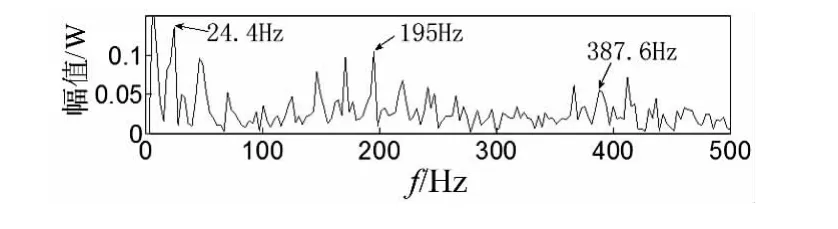
图15 第三阶本征模态信号包络谱Fig.15 Envelope spectrum of the IMF3

5 结论

由于列车与道旁监测麦克风相对高速运动带来的多普勒效应会导致列车轴承声音信号的频带扩展、频移和幅值调制问题，阻碍了对轴承运行状态的有效诊断。

本文提出的时域多普勒校正方法能有效解决由于多普勒效应而带来的上述问题，从处理结果来看，信号能够得到较好的校正;EEMD方法可以将信号分解为若干具有不同模态的本征模态函数(IMF)和余项，从处理结果来看，EEMD方法能有效提取蕴含列车轴承故障特征信息的本征模态成分。

综上，本文提出的列车轴承道旁声音监测故障诊断方法是一种有效、可行的诊断方法。

［1］Choe H C，Wan Y，Chan A K.Neural pattern identification of railroad wheel-bearing faults from audible acoustic signals:comparison of FFT，CWT and DWT features［J］.SPIE Proceedings on Wavelet Applications，1997，3087:480-496.

［2］Irani F D，吴朝院.先进道旁车辆状态监视系统的开发和应用［J］.国外铁道车辆，2002，39:39-45.Irani F D，WU Chao-yuan.Development and deployment of advanced wayside condition monitoring systems［J］.Foreign Rolling Stock，2002，39:39-45.

［3］ Barke D，Chiu W K.Structural health monitoring in the railway industry:a review［J］.Structural Health Monitoring，2005，4:81-93.

［4］ Cline J E，Bilodeau J R，Smith R L.Acoustic wayside identification of freight car roller bearing detects［C］//Proceedings of the 1998 ASME /IEEE Joint Railroad Conference，1998:79-83.

［5］ Dybała J，Radkowski S.Reduction of doppler effect for the needs of wayside condition monitoring system of railway vehicles［J］.Mechanical Systems and Signal Processing，2012，In Press， DOI:http://dx.doi.org/10.1016/j.ymssp，2012，03，003.

［6］ Stojanovic M，Catipovic J，Proakis J.Phase-coherent digital communications for underwater acoustic channels［J］.IEEE Journal of Oceanic Engineering，1994，19:100-111.

［7］杨殿阁，罗禹贡，李 兵，等.基于时域多普勒修正的运动声全息识别方法［J］.物理学报，2010，59:4738-4747.YANG Dian-ge，LUO Yu-gong，LI bing，et al.Acoustic holography method for measuring moving sound source with correction for Doppler effect in time-domain［J］.Acta Physica Sinica，2010，59:4738-4747.

［8］ Huang N E，Shen Z，Long SR，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Proceedings of the Royal Society of London.Series A:Mathematical，Physical and Engineering Sciences，1998，454:903-995.

［9］ Zhang J，Yan R，Gao R X，et al.Performance enhancement of ensemble empirical mode decomposition［J］.Mechanical Systems and Signal Processing，2010，24(7):2104-2123.

［10］陈 略，訾艳阳，何正嘉，等.总体平均经验模式分解与1.5维谱方法的研究［J］.西安交通大学学报，2009，43(5):94-98.CHEN Lue，ZI Yan-yang，HE Zheng-jia，et al.Research and application of ensemble empirical mode decomposition principle and1.5 dimension spectrum method［J］.Journal of Xi'an Jiaotong University，2009，43(5):94-98.

［11］郑 旭，郑志勇，卢兆刚，等.基于MEEMD的内燃机机体活塞敲击激励与燃烧爆发激励分离研究［J］.振动与冲击，2012，31(6):109-113.ZHENG Xu， ZHENG Zhi-yong， LU Zhao-gang， et al.Separation of piston-slap and combustion shock excitations via MEEMD method［J］.Journal of Vibration and Shock，2012，31(6):109-113.

［12］曹冲锋，杨世锡，杨将新.大型旋转机械非平稳振动信号的EEMD降噪方法［J］.振动与冲击，2009，28(9):33-38.CAO Chong-feng，YANG Shi-xi，YANG Jiang-xin.EEMD based de-noising method for the large mechanical equipment non stationary signal［J］.Journal of Vibration and Shock，2009，28(9):33-38.

［13］ Lei Y，He Z，Zi Y.Application of the EEMD method to rotor fault diagnosis of rotating machinery［J］.Mechanical Systems and Signal Processing，2009，23(4):1327-1338.

［14］Morse P M，Ingeda K U.理论声学(下)［M］.杨训仁，吕如榆，戴根华.北京:科学出版社，1986.

［15］杨殿阁，郑四发，罗禹贡，等.运动声源的声全息识别方法［J］.声学学报，2002，27:357-362.YANG Dian-ge，ZHENG Si-fa，Luo Yu-gong，et al.Acoustic holography method for the identification of moving sound source［J］.Acta Acustica，2002，27:357-362.