2 极限分析上限法原理

2 极限分析上限法原理

早在1864年Tresca提出最大剪应力屈服条件之后，塑性力学便受到了广泛的重视。但是，由于塑性力学中本构关系的复杂性，塑性力学的发展较为缓慢。直到1952年，Drucker和Prager首次提出与屈服条件相关联的流动法则后，塑性极限分析的理论和方法才得到了较大的发展。这种分析方法是将物体的本构关系简化为理想刚塑性或理想弹塑性应力-应变关系，利用刚塑性体或弹塑性体处于极限状态的普遍原理——上下限定理求解极限荷载的一种分析方法（王根龙，2002）。

在实际应用中，构筑一个静力许可的应力场来求解极限荷载的下限解比较困难，而上限法只需要构筑一个机动许可的速度场，并根据功能平衡来求解极限荷载，相对是比较容易的。通常的做法是根据功能平衡方程（虚功率方程）从所有可能的破坏模式对应的极限荷载中，找到其中最小者，从而实现以最小上限逼近结构真实的极限荷载。本文将围绕着建立协调速度场这一思路，通过极限分析上限法与边坡工程的结合开展相关的研究工作。

2.1 极限分析上限定理的基本假定

理想刚塑性体和理想弹塑性体在荷载（包括外部荷载和物体自重）作用下，当荷载达到某一数值并保持不变的情况下，物体将发生“无限”的变形（见图2-1），或者说物体已进入塑性流动状态。在小变形的假设条件下，通常所称的极限状态可以理解为开始产生塑性流动时的瞬间状态，此时的变形仍然是很小的。极限状态对应的荷载称为极限荷载（龚晓南，1997）。

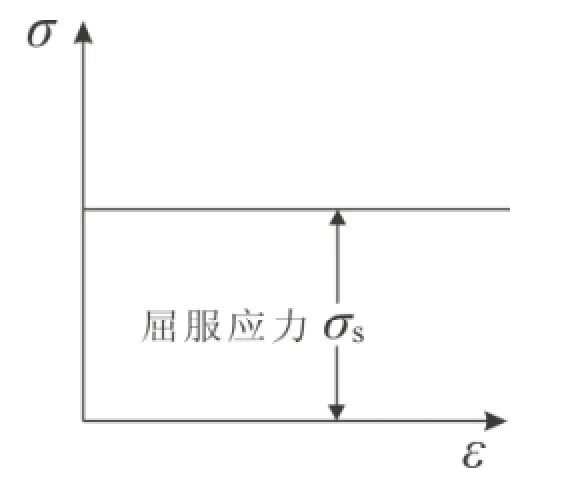
图2-1 刚塑性体的应力-应变关系

在岩土体工程中，岩土材料通常采用库仑（Coulomb）材料的屈服函数，相应的岩土材料服从库仑屈服条件。库仑屈服函数有两种表达方式，分别为

式中：c为材料的黏聚力；φ为材料的内摩擦角；σn为法向应力；τ为剪应力；f为屈服函数。

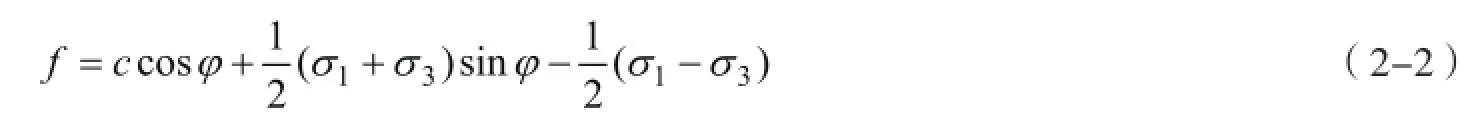
式中：σ1，σ3分别为最大主应力和最小主应力；其他符号意义同前。

在塑性流动状态或屈服状态下，根据土塑性理论可知，屈服应力与塑性应变之间没有直接的关系。因此，需要确定的不是应变，而是应变率。屈服应力与相应的塑性应变率之间的关系可由库仑材料服从的相关联流动法则确定。根据库仑材料屈服函数的两种表达方式，屈服应力与相应的塑性应变率之间的关系也有两种表达方式（郑颖人，2002）。

第一种表达方式为

将库仑材料的屈服函数表达式（2-1）代入式（2-3）中，可得

第二种表达方式为

将库仑材料的屈服函数表达式（2-2）代入式（2-5）中，可得

由假设条件得到的式（2-4）和式（2-5）可以说明一个问题，即库仑材料（岩土材料，φ≠0）发生塑性流动时，体积应变不等于零，产生了剪胀现象。这种剪胀现象必然伴随着内能的耗散，并且内能的耗散是由外力（包括自重）做功产生的，存在着内能耗散与外力所做的功率相等的基本关系。

2.2 机动许可速度场

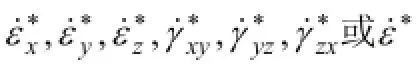
（1）在塑性变形区Ω内满足几何方程，用公式表示为

（3）满足外功率为正的条件。

满足上述三个条件的速度场称为机动许可的速度场，但它不一定是真实可能发生的速度场，因为该速度场不一定满足平衡条件的应力场。显然，物体在荷载作用下处于极限状态时，其真实的速度场必定是机动许可的速度场。同时满足以上三个条件的机动许可的速度场有多个，并且这多个机动许可的速度场一定包括了真实状态的速度场。

2.3 极限分析的虚功率方程

2.3.1 体积塑性耗散功率的虚功率方程

物体在极限荷载下产生的几何变形很小（符合小变形的假设），而小变形假设则意味着可以采用以速率形式表示的虚功方程——虚功率方程（Chen，1975；Yu，1998）。其公式可表示为

这个公式的物理意义为应力在应变率上的功率，可以用图2-2来说明。取微小六面体（单元体），左右两面上作用有应力σv，如图2-2（a）所示，假定单元体在y方向的缩短应变率为，则在单位时间内沿y方向单元体的缩短距离为，所以σv在y方向所做的功率为，当六面体为单元体时，应力σv在应变率上的功率为。同理可知及的物理意义。假定单元体的上、下、左、右四个面上作用有剪应力τyz=τzy，假设左面不动，如图2-2（b）所示，则右面相对于左面下移，右面上的剪切内力为τyzdxdz，因此，剪切内力所做的功率为，当六面体为单元体时，剪应力τyz在剪应变率上的功率为，同理可知及的物理意义。

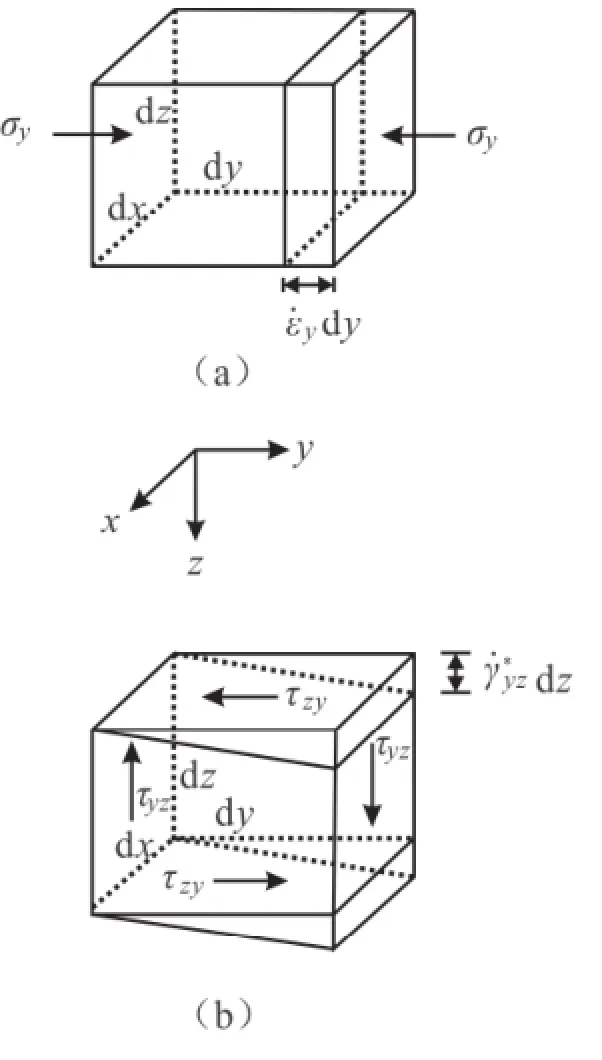
图2-2 虚功率

假定土体为理想塑性体，则在应力空间其屈服面为凸，且满足相关联法则，即

式中：σij为应力张量；为塑性应变速率；f(σij)为屈服条件；为非负乘子。

对于满足摩尔-库仑（Mohr-Coulomb）屈服条件及其相关联流动法则的岩土体，在平面变形条件下，其屈服条件可写为

根据式（2-10）得

2.3.2 面积塑性耗散功率的虚功率方程

速度间断面可以看作是一个薄层塑性变形区，速度在层内发生急剧而连续的变化。因此，在该薄层塑性变形区内将有内能的耗散。只要能合理地计算出能量耗损，速度间断也是允许的，这种间断面可以被认为是连续速度场的极限情况。在这种情况下，速度分量（一个或多个）在跨越窄过渡层时变化很快，因而为了方便起见，可以用间断面来代替。间断速度场不仅提供了方便，而且往往还可获得实际的破坏模式或破坏机制。

沿速度间断面内能的耗散率计算（见图2-3），是将薄层的塑性变形区视为速度间断面，而将两侧视为刚体。对于库仑材料（岩土材料）单位体积能量耗散率D可表示为

式中：D为岩土材料的单位体积能量耗散率；σn为法向应力；τ为剪应力；为塑性应变率的剪切应变率分量；为塑性应变率的法向应变率分量。

图2-3 速度间断面内能耗散率计算图

将式（2-16）代入式（2-4）中，整理后可得到D的另一种表达式：

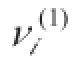
式（2-18）表明间断面两侧的相对速度与间断面切线方向成φ角，考虑存在速度间断面对虚功率方程的影响，需要计算在速度间断面上的内能耗散率。以图2-3为例，塑性变形区内总的能量消散率为

因此，当同时考虑塑性变形区内和速度间断面上的能量消散率时（李广信，2004），虚功率方程可表示为

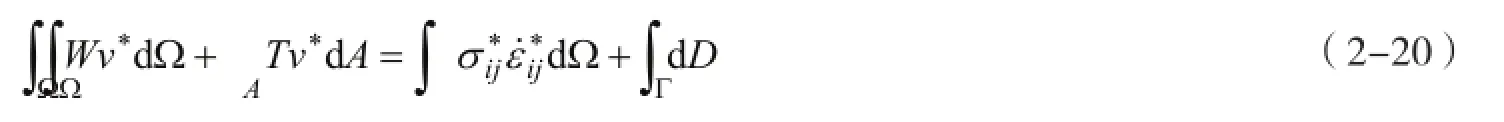
2.4 极限分析塑性力学上限定理

上限定理是指在所有机动许可的速度场对应的荷载中，极限状态的荷载是其中最小的一个，或者说，根据上限定理求得的荷载值是极限破坏状态荷载的一个上限值。

对于边坡而言，假定在坡体表面作用有一个外荷载，不断增加此外荷载至T，边坡最终达到极限状态。此时的外荷载T称为极限荷载。我们认定，T达到极限状态时，边坡内出现了一个塑性区Ω和一个弹性区E。在塑性区Ω内，处处达到极限平衡，而在弹性区E内，各点均处于弹性状态。根据刚塑性的假定条件，可以认为在弹性区域E内各点的位移值为零。在Ω和E和之间，出现了一个位移间断面Γ，通常称为边坡的滑裂面（陈祖煜，2005）（见图2-4）。

图2-4 边坡破坏机构

塑性力学的上限定理为边坡稳定极限分析方法提供了理论基础，这一理论体系的基本假定包括：

（1）假定材料是理想刚塑性体。岩土材料在进入极限平衡状态后，可能发生较大的塑性变形，与其相比弹性变形可以忽略；并且材料在塑性流动时不会出现应变硬化和应变软化特性。因此，在极限分析领域，总是假定塑性变形为结构的总变形。

（2）小变形假定。岩土材料在发生屈服的瞬间变形很小，同时要求满足变形协调条件的应变场，除个别特殊规定的部位外，均应连续可微。

（3）完全塑性区假定。当边坡处于极限状态时，假定在边坡内存在一个完全塑性区与弹性区，其分界面即为滑裂面。尽管这一假定可能过高地估计了边坡的抗滑能力，但大量的工程实践表明，这一假定还是基本合理的。

（4）材料在屈服时服从摩尔-库仑屈服准则与相关联流动法则。材料在屈服时服从摩尔-库仑屈服准则和相关联流动法则，这就意味着Drucker公设的成立。Drucker公设是塑性力学上、下限定理成立的一个关键依据。

（5）主应力轴与主应变轴重合的假定。在推导滑面上的内能耗散公式时，实质上是假定了滑裂面上的剪应力、剪应变与法向量共面的假定，这一假定也隐含了同一单元的主应力轴与主应变轴方向重合的假定。

以下通过反证法来证明边坡塑性极限分析上限定理。将式（2-19）代入式（2-20）中，可得到虚功率方程的表达式为

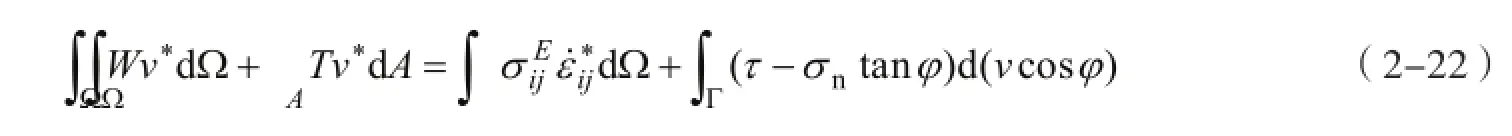
用式（2-21）减去式（2-22），可得

据相关联流动法则有

很显然，式（2-24）和式（2-25）与式（2-23）相矛盾，即原假定是错误的。这就证明了与任何一个机动许可的速度场对应的荷载都将大于或等于真实的极限荷载，因此，上限定理得到了证明。

由上限定理可知，如果物体按某一形式破坏，即存在内能耗散不比外力功率大的变形状态，由于此时物体已经破坏，由此所得的荷载一般为极限荷载的上限。在应用上限定理时，一般是先假定一个破坏速度场，并使外力在假定的速度场上做正功，然后利用内能耗散与外力功率相等的原理求出与破坏速度场对应的荷载。由此所得的荷载值不会小于真实的极限荷载。

在边坡稳定性分析过程中，应用上限定理求解稳定系数时，需利用荷载（包括自重荷载W和外部作用荷载T）在机动许可的速度场上的外力功率与坡体内部及速度间断面上的内能耗散率相等的原理（虚功率方程），建立起关系式。